Pesquisa em Memria Primria rvores AVL David Menotti

Pesquisa em Memória Primária – Árvores AVL David Menotti Algoritmos e Estruturas de Dados I v DECOM – UFOP 6 8 3 4 z

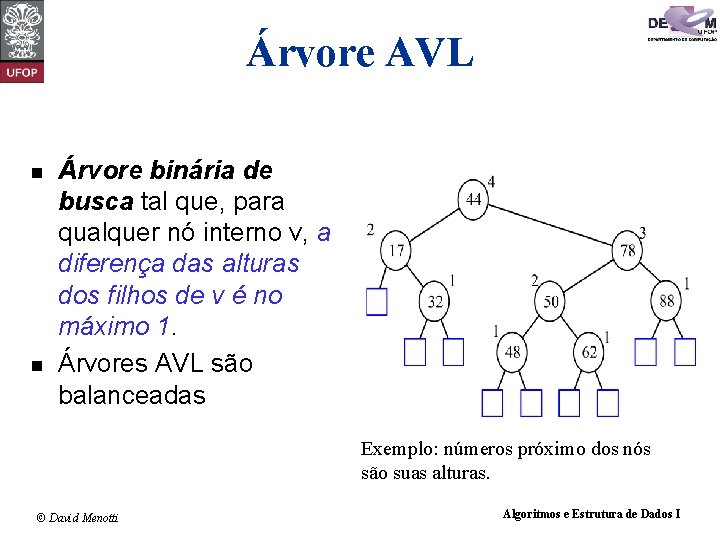
Árvore AVL n n Árvore binária de busca tal que, para qualquer nó interno v, a diferença das alturas dos filhos de v é no máximo 1. Árvores AVL são balanceadas Exemplo: números próximo dos nós são suas alturas. © David Menotti Algoritmos e Estrutura de Dados I

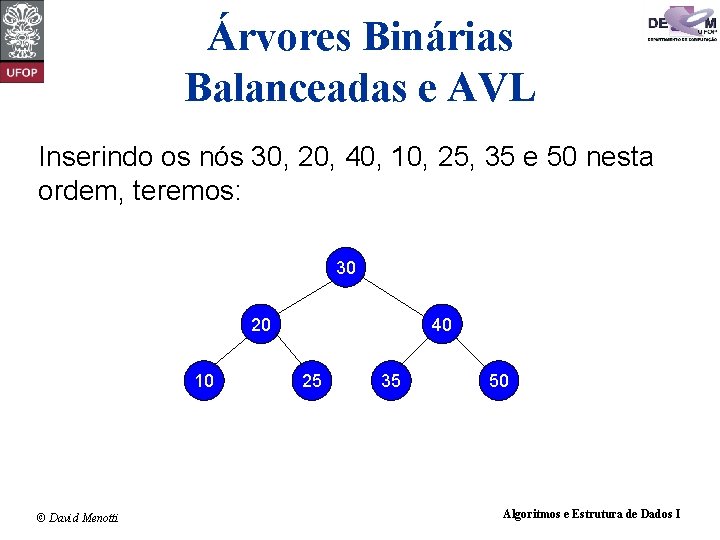
Árvores Binárias Balanceadas e AVL Inserindo os nós 30, 20, 40, 10, 25, 35 e 50 nesta ordem, teremos: 30 20 10 © David Menotti 40 25 35 50 Algoritmos e Estrutura de Dados I

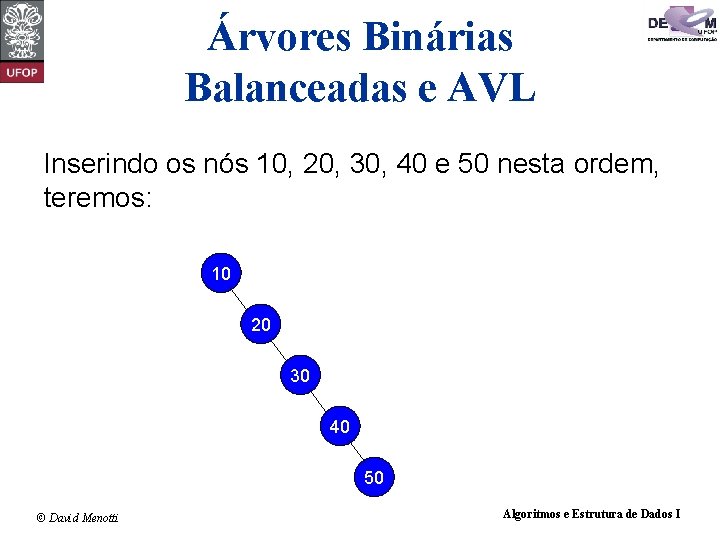
Árvores Binárias Balanceadas e AVL Inserindo os nós 10, 20, 30, 40 e 50 nesta ordem, teremos: 10 20 30 40 50 © David Menotti Algoritmos e Estrutura de Dados I

Árvores Binárias Balanceadas • • • Existem ordens de inserção de nós que conservam o balanceamento de uma árvore binária. Na prática é impossível prever essa ordem ou até alterá-la. Algoritmos para balanceamentos. © David Menotti Algoritmos e Estrutura de Dados I

Árvores Binárias Balanceadas • • • A vantagem de uma árvore balanceada com relação a uma degenerada está em sua eficiência. Por exemplo: numa árvore binária degenerada de 10. 000 nós são necessárias, em média, 5. 000 comparações (semelhança com arrays ordenados e listas encadeadas). Numa árvore balanceada com o mesmo número de nós essa média reduz-se a 14 comparações. © David Menotti Algoritmos e Estrutura de Dados I

AVL • • • Algoritmo de balanceamento de árvores binárias. A origem da denominação AVL vem dos seus dois criadores: Adel’son-Vel’skii e Landis. Ano de divulgação: 1962. © David Menotti Algoritmos e Estrutura de Dados I

TAD-Árvore AVL n Estrutura de dados: typedef long Tipo. Chave; typedef struct Registro { Tipo. Chave; /* outros componentes */ } Registro; typedef Struct No { Registro Reg; Apontador p. Esq, p. Dir; } No; typedef struct No * Apontador; typedef Apontador Tipo. Dicionario; © David Menotti Algoritmos e Estrutura de Dados I

Árvores AVL • • Uma árvore binária balanceada é aquela na qual, para cada nó, as alturas de suas sub-árvores esquerda e direita diferem de, no máximo, 1. Fator de balanceamento (FB) de um nó é a diferença entre a altura da sub-árvore esquerda em relação à subárvore direita. FB(p) = altura(sub-árvore esquerda de p) - altura(sub-árvore direita de p) • Em uma árvore binária balanceada todos os FB de todos os nós estão no intervalo -1 FB 1 © David Menotti Algoritmos e Estrutura de Dados I

FB e Altura int FB (TNo* p. Raiz) { if (p. Raiz == NULL) return 0; int Altura(TNo* p. Raiz) { int i. Esq, i. Dir; if (p. Raiz == NULL) return 0; return Altura(p. Raiz->p. Esq) - Altura(p. Raiz->p. Dir); } i. Esq = Altura(p. Raiz->p. Esq); i. Dir = Altura(p. Raiz->p. Dir); if ( i. Esq > i. Dir ) return i. Esq + 1; else return i. Dir + 1; } © David Menotti Algoritmos e Estrutura de Dados I

AVL • • Inicialmente inserimos um novo nó na árvore normalmente. A inserção deste pode degenerar a árvore. A restauração do balanceamento é feita através de rotações na árvore no nó “pivô”. Nó “pivô” é aquele que após a inserção possui Fator de Balanceamento fora do intervalo. © David Menotti Algoritmos e Estrutura de Dados I

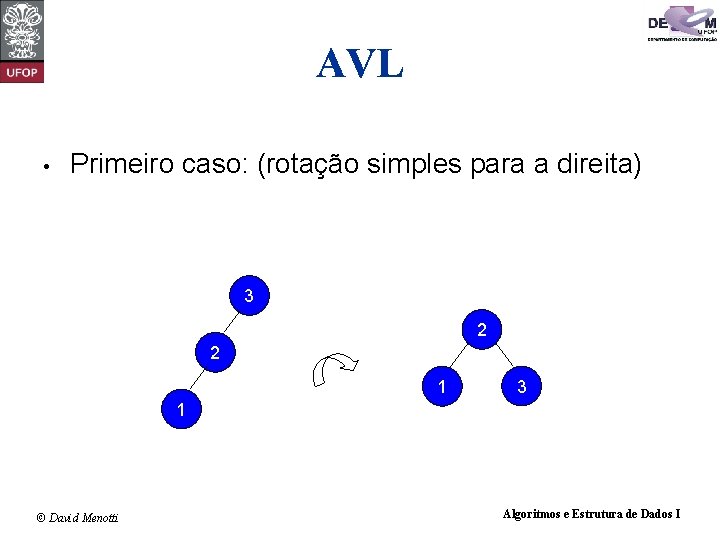
AVL • Primeiro caso: (rotação simples para a direita) • • • FB > 1 (subárvore esquerda maior que subárvore direita) E a subárvore esquerda desta subárvore esquerda é maior que a subárvore direita dela Então realizar uma rotação simples para a direita. 3 2 1 © David Menotti Algoritmos e Estrutura de Dados I

AVL • Primeiro caso: (rotação simples para a direita) 3 2 2 1 3 1 © David Menotti Algoritmos e Estrutura de Dados I

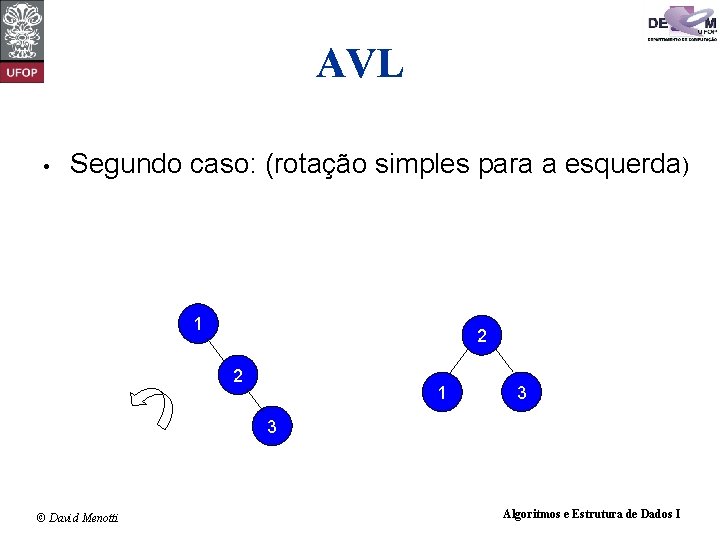
AVL • Segundo caso: (rotação simples para a esquerda) • • • FB < -1 (subárvore esquerda menor que subárvore direita) E a subárvore direita desta subárvore direita é maior que a subárvore esquerda dela Então realizar uma rotação simples para a esquerda. 1 2 3 © David Menotti Algoritmos e Estrutura de Dados I

AVL • Segundo caso: (rotação simples para a esquerda) 1 2 2 1 3 3 © David Menotti Algoritmos e Estrutura de Dados I

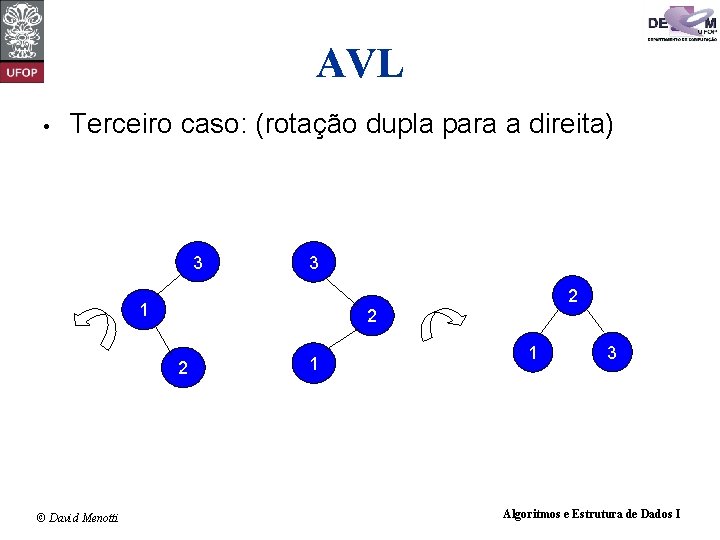
AVL • Terceiro caso: (rotação dupla para a direita) • • • FB > 1 (subárvore esquerda maior que subárvore direita) E a subárvore esquerda desta subárvore esquerda é menor ou igual que a subárvore direita dela Então realizar uma rotação dupla para a direita. 3 1 2 © David Menotti Algoritmos e Estrutura de Dados I

AVL • Terceiro caso: (rotação dupla para a direita) 3 3 2 1 2 2 © David Menotti 1 1 3 Algoritmos e Estrutura de Dados I

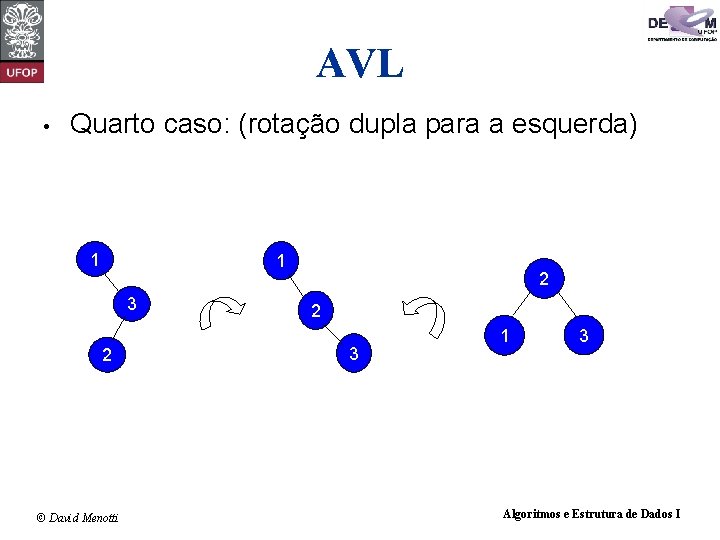
AVL • Quarto caso: (rotação dupla para a esquerda) • • • FB < -1 (subárvore esquerda menor que subárvore direita) E a subárvore direita desta subárvore direita é menor que a subárvore esquerda dela Então realizar uma rotação dupla para a esquerda. 1 3 2 © David Menotti Algoritmos e Estrutura de Dados I

AVL • Quarto caso: (rotação dupla para a esquerda) 1 1 3 2 © David Menotti 2 2 3 1 3 Algoritmos e Estrutura de Dados I

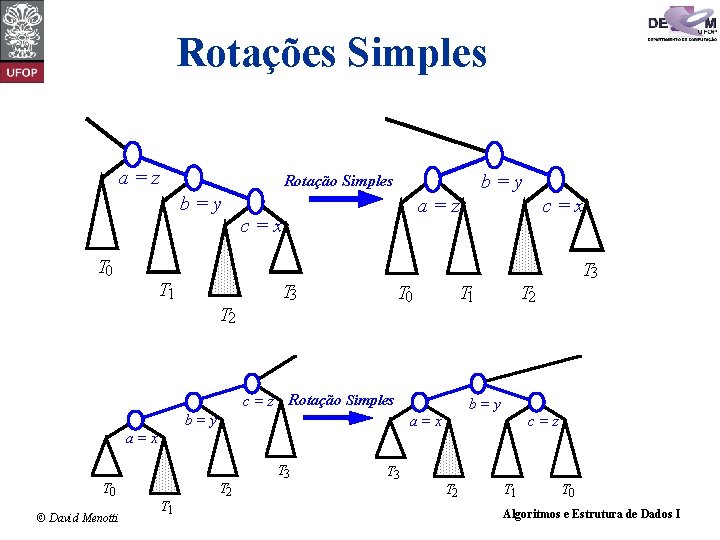
Rotações Simples a=z b=y T 0 b=y Rotação Simples T 1 T 2 a=z c=x T 3 T 0 T 1 c = z Rotação Simples b=y c=x T 3 T 2 b=y a=x c=z a=x T 0 © David Menotti T 1 T 2 T 3 T 2 T 1 T 0 Algoritmos e Estrutura de Dados I

Rotações Simples void RSE(TNo** pp. Raiz) { TNo *p. Aux; p. Aux = (*pp. Raiz)->p. Dir; (*pp. Raiz)->p. Dir = p. Aux->p. Esq; p. Aux->p. Esq = (*pp. Raiz); (*pp. Raiz) = p. Aux; } void RSD(TNo** pp. Raiz) { TNo *p. Aux; p. Aux = (*pp. Raiz)->p. Esq; (*pp. Raiz)->p. Esq = p. Aux->p. Dir; p. Aux->p. Dir = (*pp. Raiz); (*pp. Raiz) = p. Aux; } © David Menotti Algoritmos e Estrutura de Dados I

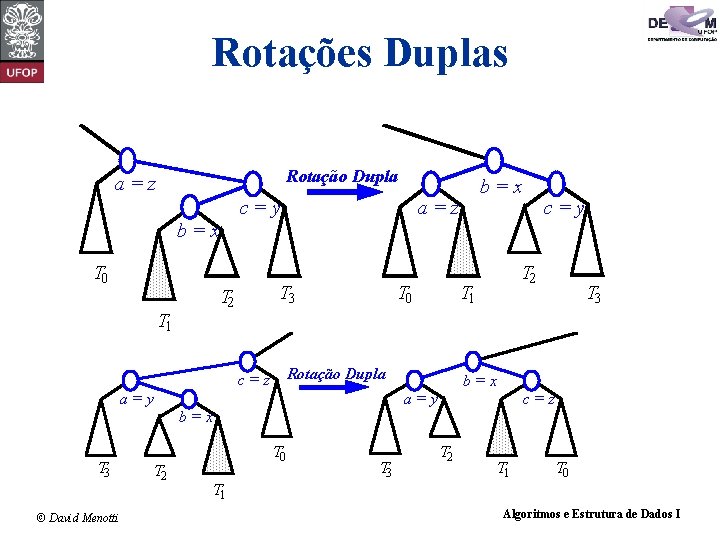
Rotações Duplas Rotação Dupla a=z c=y b=x T 0 T 3 T 2 T 1 T 0 T 1 Rotação Dupla c=z a=y T 2 T 3 b=x a=y c=z b=x T 3 © David Menotti T 2 T 0 T 3 T 2 T 1 T 0 T 1 Algoritmos e Estrutura de Dados I

Rotações Duplas int Balanca. Esquerda(TNo** pp. Raiz) { int fbe = FB ( (*pp. Raiz)->p. Esq ); if ( fbe > 0 ) { RSD(pp. Raiz); return 1; } else if (fbe < 0 ) { /* Rotação Dupla Direita */ RSE( &((*pp. Raiz)->p. Esq) ); RSD( pp. Raiz ); /* &(*pp. Raiz) */ return 1; } return 0; } © David Menotti int Balanca. Direita(TNo** pp. Raiz) { int fbd = FB( (*pp. Raiz)->p. Dir); if ( fbd < 0 ) { RSE (pp. Raiz); return 1; } else if (fbd > 0 ) { /* Rotação Dupla Esquerda */ RSD( &((*pp. Raiz)->p. Dir) ); RSE( pp. Raiz ); /* &(*pp. Raiz) */ return 1; } return 0; } Algoritmos e Estrutura de Dados I

Balanceamento int Balanceamento(TNo** pp. Raiz) { int fb = FB(*pp. Raiz); if ( fb > 1) return Balanca. Esquerda(pp. Raiz); else if (fb < -1 ) return Balanca. Direita(pp. Raiz); else return 0; } © David Menotti Algoritmos e Estrutura de Dados I

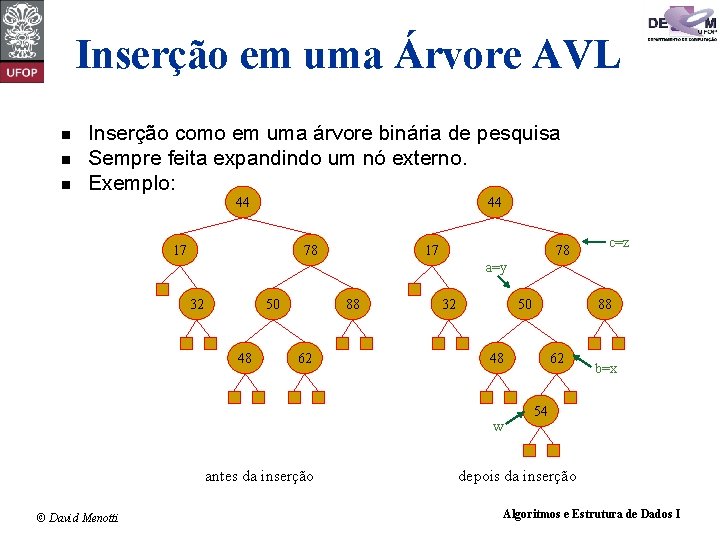
Inserção em uma Árvore AVL n n n Inserção como em uma árvore binária de pesquisa Sempre feita expandindo um nó externo. Exemplo: 44 44 17 78 c=z a=y 32 50 48 88 62 32 50 48 w antes da inserção © David Menotti 88 62 b=x 54 depois da inserção Algoritmos e Estrutura de Dados I

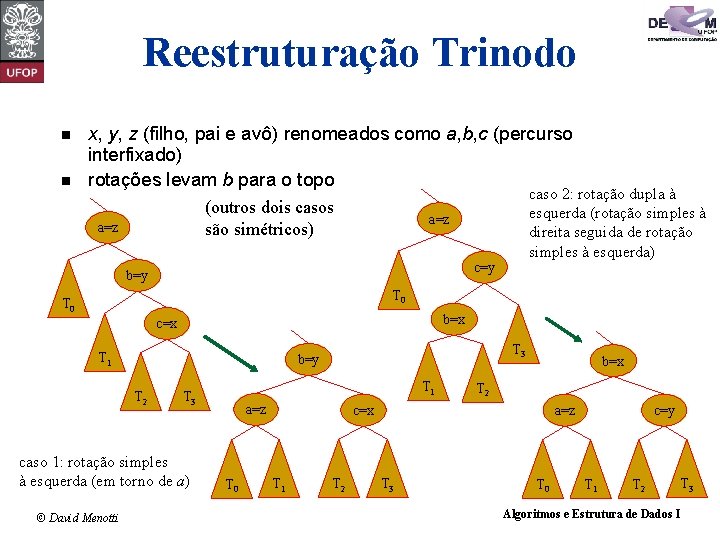
Reestruturação Trinodo n n x, y, z (filho, pai e avô) renomeados como a, b, c (percurso interfixado) rotações levam b para o topo (outros dois casos são simétricos) a=z caso 2: rotação dupla à esquerda (rotação simples à direita seguida de rotação simples à esquerda) a=z c=y b=y T 0 b=x c=x T 1 T 2 T 1 T 3 caso 1: rotação simples à esquerda (em torno de a) © David Menotti T 3 b=y a=z T 0 b=x T 2 c=x T 1 T 2 a=z T 3 T 0 c=y T 1 T 2 T 3 Algoritmos e Estrutura de Dados I

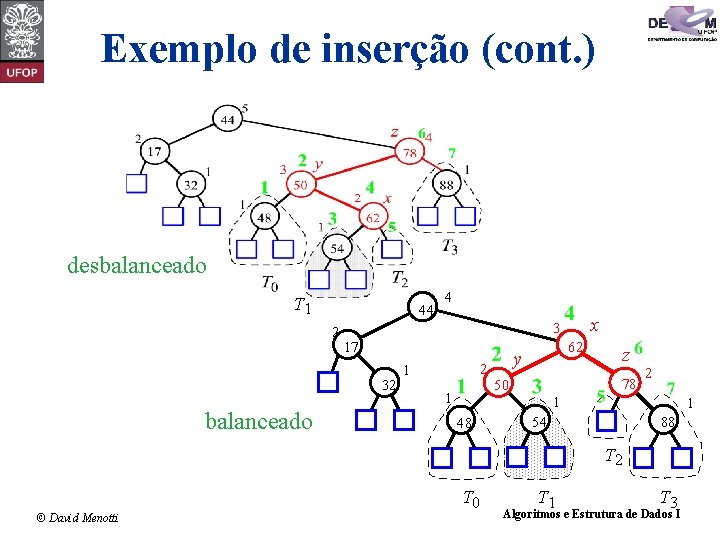
Exemplo de inserção (cont. ) desbalanceado T 1 44 2 x 3 17 32 balanceado 4 2 1 1 48 62 y z 78 50 2 1 1 54 88 T 2 © David Menotti T 0 T 1 T 3 Algoritmos e Estrutura de Dados I

Inserção int Insere(TNo** pp. Raiz, Registro* x) { if (*pp. Raiz == NULL) { *pp. Raiz = (TNo*)malloc(sizeof(TNo)); (*pp. Raiz)->Reg = *x; (*pp. Raiz)->p. Esq = NULL; (*pp. Raiz)->p. Dir = NULL; return 1; } else if ( (*pp. Raiz)->Reg. chave > x->chave ) { if ( Insere(&(*pp. Raiz)->p. Esq, x) ) { if (Balanceamento(pp. Raiz)) return 0; else return 1; } } } © David Menotti else if ( (*pp. Raiz)->Reg. chave < x->chave ) { if ( Insere(&(*pp. Raiz)->p. Dir, x) ) { if (Balanceamento(pp. Raiz)) return 0; else return 1; } else return 0; /* valor jah presente */ Algoritmos e Estrutura de Dados I

Implementação de Inserção n Cálculo de fatores de balanceamento q n Custo: O(log n) ? ? Como melhorar? q Cada nó: q q q Fator de balanceamento Profundidade x Altura Problema: atualizar dados durante rotações © David Menotti Algoritmos e Estrutura de Dados I

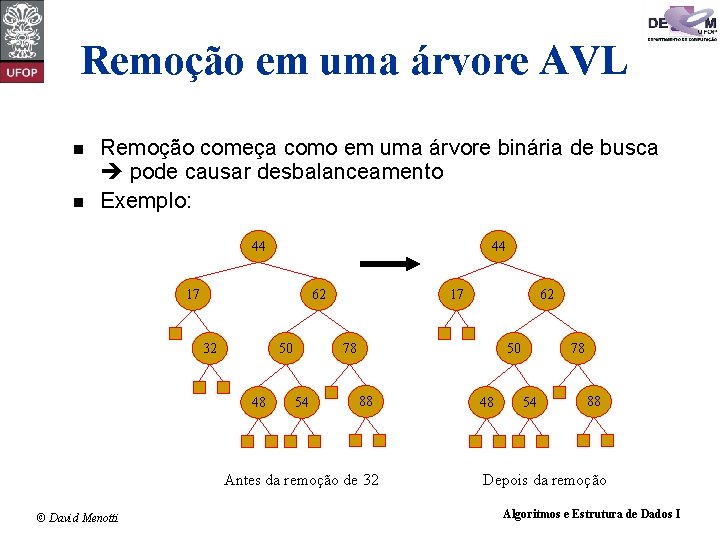
Remoção em uma árvore AVL n n Remoção começa como em uma árvore binária de busca pode causar desbalanceamento Exemplo: 44 44 17 62 32 50 48 17 78 54 50 88 Antes da remoção de 32 © David Menotti 62 48 78 54 88 Depois da remoção Algoritmos e Estrutura de Dados I

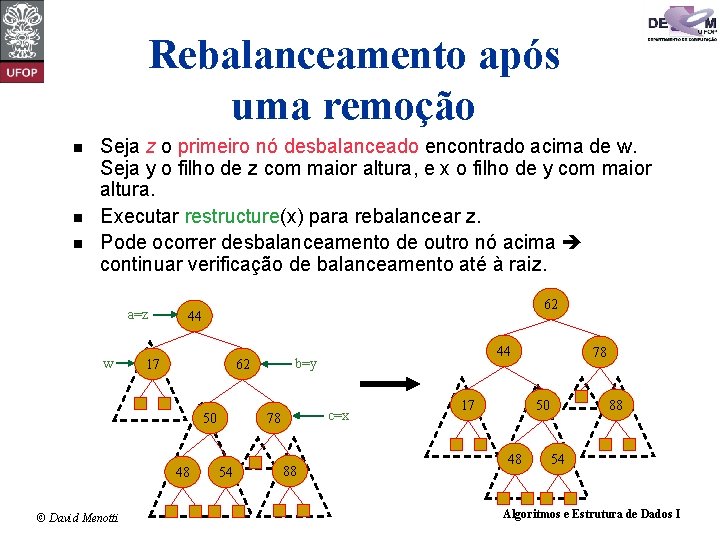
Rebalanceamento após uma remoção n n n Seja z o primeiro nó desbalanceado encontrado acima de w. Seja y o filho de z com maior altura, e x o filho de y com maior altura. Executar restructure(x) para rebalancear z. Pode ocorrer desbalanceamento de outro nó acima continuar verificação de balanceamento até à raiz. a=z w 62 44 17 48 © David Menotti b=y 62 50 c=x 78 54 44 88 17 78 50 48 88 54 Algoritmos e Estrutura de Dados I

Tempos de execução para árvores AVL n n uma única reestruturação é O(1) q usando uma árvore binária implementada com estrutura ligada pesquisa é O(log n) q altura de árvore é O(log n), não necesita reestruturação inserir é O(log n) q busca inicial é O(log n) q reestruturação para manter balanceamento é O(log n) remove é O(log n) q busca inicial é O(log n) q reestruturação para manter balanceamento é O(log n) © David Menotti Algoritmos e Estrutura de Dados I

Verificação n Verifica se árvore é AVL int Eh. Arvore. Arvl(TNo* p. Raiz) { int fb; if (p. Raiz == NULL) return 1; if (!Eh. Arvore. Arvl(p. Raiz->p. Esq)) return 0; if (!Eh. Arvore. Arvl(p. Raiz->p. Dir)) return 0; fb = FB (p. Raiz); if ( ( fb > 1 ) || ( fb < -1) ) return 0; else return 1; } © David Menotti Algoritmos e Estrutura de Dados I

Aplicações n Para que servem as Árvores Binárias? n Exemplos de aplicações: q Redes de Comunicação de Dados q q Envio de pacotes ordenados e/ou redundantes Codificação de Huffman q © David Menotti Compressão e Descompressão de arquivos Algoritmos e Estrutura de Dados I

1) Redes de Comunicação n n n A maioria dos protocolos de comunicação fragmenta as mensagens em pacotes que são numerados e enviados através da rede Não há garantia da chegada em ordem dos pacotes Perdas de pacotes geram novos envios e estes podem causar duplicatas dos mesmos © David Menotti Algoritmos e Estrutura de Dados I

Reconstrução da Mensagem n Como reconstruir a mensagem corretamente? q q n Descartar os pacotes repetidos Ordenar os pacotes Como implementar tal algoritmo? q Utilizando Árvores Binárias © David Menotti Algoritmos e Estrutura de Dados I

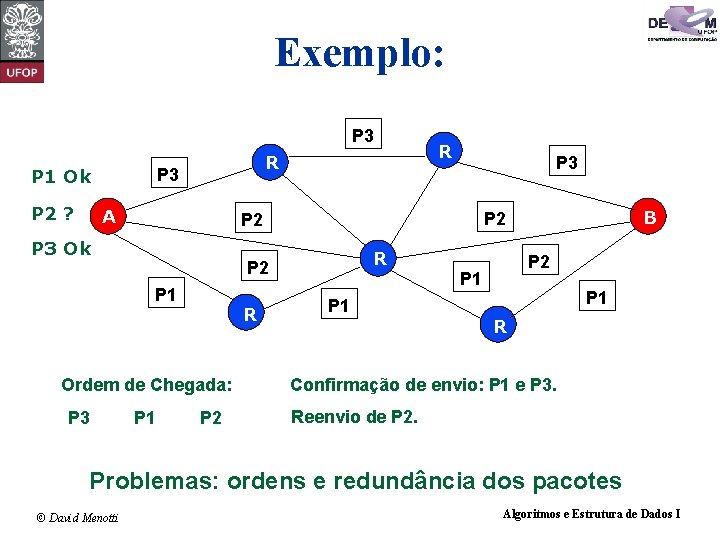
Exemplo: P 3 P 1 Ok P 2 ? R A P 3 R P 2 P 1 R Ordem de Chegada: P 1 P 2 B P 2 P 3 Ok P 3 R P 2 P 1 P 1 R Confirmação de envio: P 1 e P 3. Reenvio de P 2. Problemas: ordens e redundância dos pacotes © David Menotti Algoritmos e Estrutura de Dados I

Algoritmo n n O primeiro pacote é colocado na raiz da árvore. Cada pacote sucessivo é comparado com o da raiz Se for igual, descarta-se a réplica. Se for menor ou maior, percorre-se os lados esquerdo ou direito da árvore Sub-árvore vazia implica inserção do novo pacote Sub-árvore não vazia implica comparação dos pacotes com a mesma © David Menotti Algoritmos e Estrutura de Dados I

Problemas resolvidos? n Problema da ordenação q n A ordenação dos pacotes pode ser feita trivialmente com apenas uma chamada ao método in. Order() da árvore binária Problema da redundância q Solucionado com o algoritmo de inserção na árvore, visto que o pacote, antes de ser inserido, é comparado com os demais que já se encontram na árvore binária © David Menotti Algoritmos e Estrutura de Dados I

2) Codificação de Huffman n n Algoritmo utilizado para comprimir arquivos Todo o algoritmo é baseado na criação de uma Árvore Binária Programas como Winzip e Win. RAR utilizam este algoritmo Criado por David Huffman em 1952 © David Menotti Algoritmos e Estrutura de Dados I

Códigos e Caracteres n n Caracteres são letras, números e símbolos Códigos são seqüências de bits que podem representar de maneira ÚNICA um caracter b bits para representar c caracteres: b c = 2 Exemplos: ASCII (7 bits) 7 2 = 128 caracteres © David Menotti Extended ASCII (8 bits) 8 2 = 256 caracteres Algoritmos e Estrutura de Dados I

Como comprimir arquivos? No código ASCII, todos os caracteres têm um número fixo de bits n Números variáveis de bits implica menor capacidade de armazenamento n Associações com bits variáveis podem comprimir consideravelmente o arquivo G Como comprimir arquivos desta maneira? C Utilizando a Codificação de Huffman! n © David Menotti Algoritmos e Estrutura de Dados I

Exemplo: l Considere o arquivo com o seguinte texto: AAAAABBBBCCCCCCDDDDDEE n n n Freqüências: A = 10; B = 8; C = 6; D = 5; E = 2 Construção da Árvore Binária Comparação do número de bits q q Tamanho Fixo (8 bits) Total = 248 bits Tamanho Variável Total = 69 bits © David Menotti Algoritmos e Estrutura de Dados I

Compressão n n n Depois da geração da árvore, o arquivo é percorrido novamente e cada caracter do arquivo é substituído pelo código binário contido na árvore, gerando uma cadeia de bits Criação da tabela de caracteres e códigos binários O que é armazenado? q q Cadeia de bits gerada Tabela de caracteres e códigos © David Menotti Algoritmos e Estrutura de Dados I

Descompressão n n Regeneração da árvore binária através da tabela de caracteres e códigos A cadeia de bits é percorrida e, à medida que uma sub-cadeia é encontrada na tabela de caracteres e códigos, a mesma é substituída pelo caracter correspondente © David Menotti Algoritmos e Estrutura de Dados I

Conclusões n n As árvores binárias são uma das estruturas de dados mais importantes devido a grande aplicabilidade das mesmas. A maioria dos algoritmos das árvores binárias são de simples entendimento, facilitando sobremaneira o desenvolvimento de sistemas. © David Menotti Algoritmos e Estrutura de Dados I