PERTEMUAN KE2 Penggunaan Matriks dan Transformasi Linear dalam






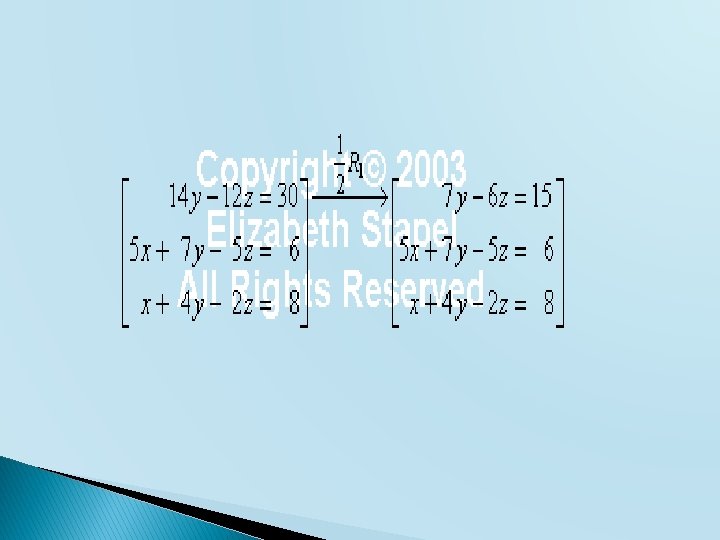


































- Slides: 52

PERTEMUAN KE-2 Penggunaan Matriks dan Transformasi Linear dalam Masalah Geometri dan Komputasi OLEH KBK ALJABAR

Apa yang Anda lihat dalam gambar ini ?

Transformasi Linear

TENTANG MATRIKS � Mengapa matriks? � Operasi matriks : jumlahan dan perkalian � Invers � Determinan Matriks

Motivasi pemakaian matriks dalam mencari penyelesaian SPL � Jawaban : – 3 x + 2 y – 6 z = 6……(1) 5 x + 7 y – 5 z = 6……. (2) x + 4 y – 2 z = 8……. (3)

Apa sebenarnya yang terjadi dalam proses eliminasi ?
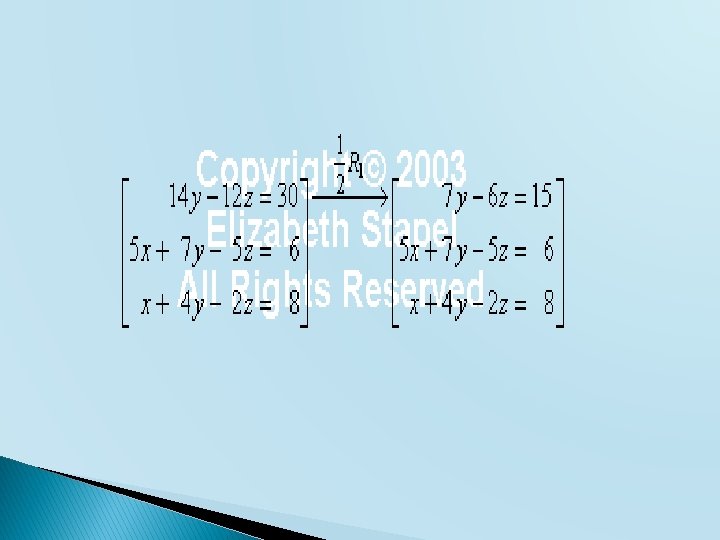


Lihat selengkapnya …… � Tambahan Motivasi (Pertemuan 2). docx

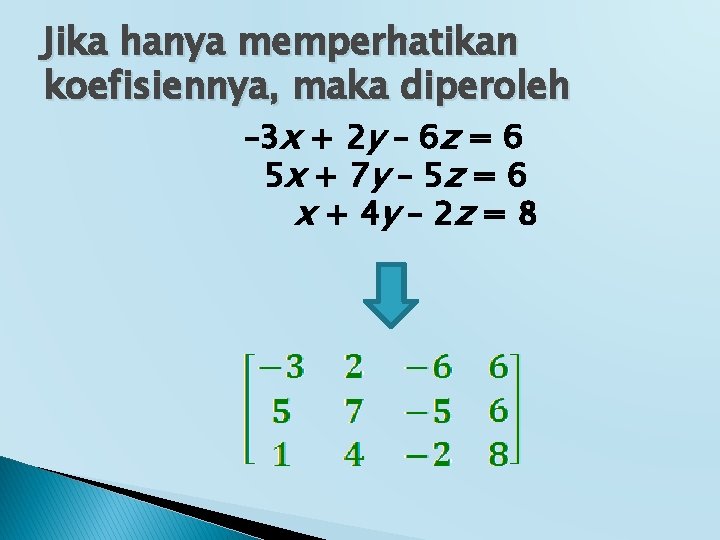
Jika hanya memperhatikan koefisiennya, maka diperoleh – 3 x + 2 y – 6 z = 6 5 x + 7 y – 5 z = 6 x + 4 y – 2 z = 8



MATRIKS adalah…. . himpunan bilangan real (atau kompleks) yang disusun membentuk persegi panjang.

Contoh-contoh Matriks

Komponen yang terdapat dalam sebuah matriks 1. Ukuran atau ordo matriks � Dinyatakan dalam m x n; �m menyatakan banyaknya baris dan n menyatakan banyaknya kolom matriks tersebut. 2. Elemen-elemen suatu matriks

Contoh ukuran matriks adalah matriks berukuran 2 x 2 adalah matriks berukuran 3 x 2

Jenis-jenis Matriks (1) � Matriks bujursangkar n x n � Matriks diagonal

Jenis-jenis Matriks (2) � Matriks segitiga atas � Matriks simetri

Notasi suatu matriks menyatakan elemen matriks A pada posisi baris ke-i dan kolom ke-j

Operasi Penjumlahan Matriks

Contoh penjumlahan matriks � Catatan : ukuran matriks harus sama.

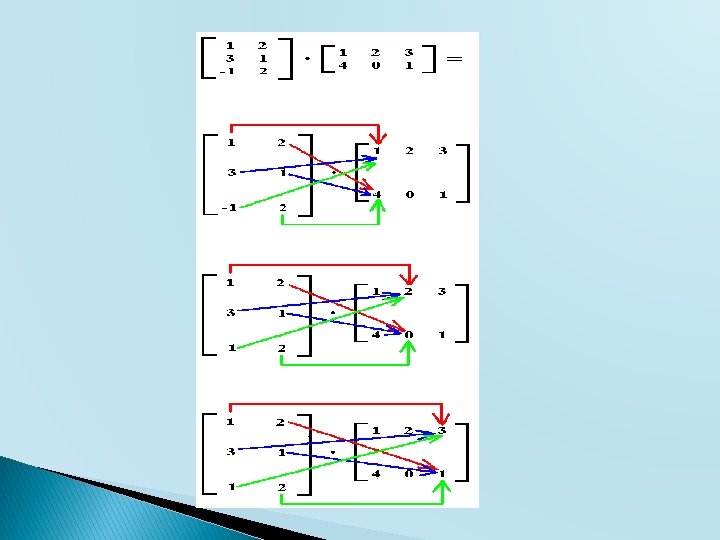
Motivasi perkalian matriks – 3 x + 2 y – 6 z = 6 5 x + 7 y – 5 z = 6 x + 4 y – 2 z = 8



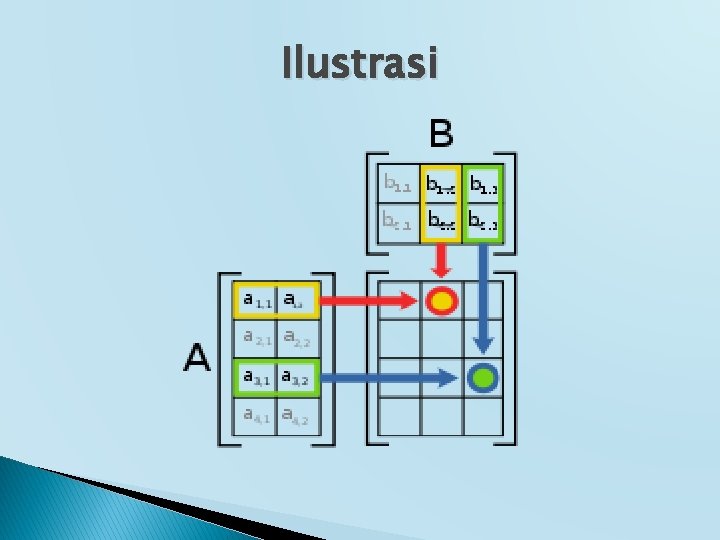
Ilustrasi

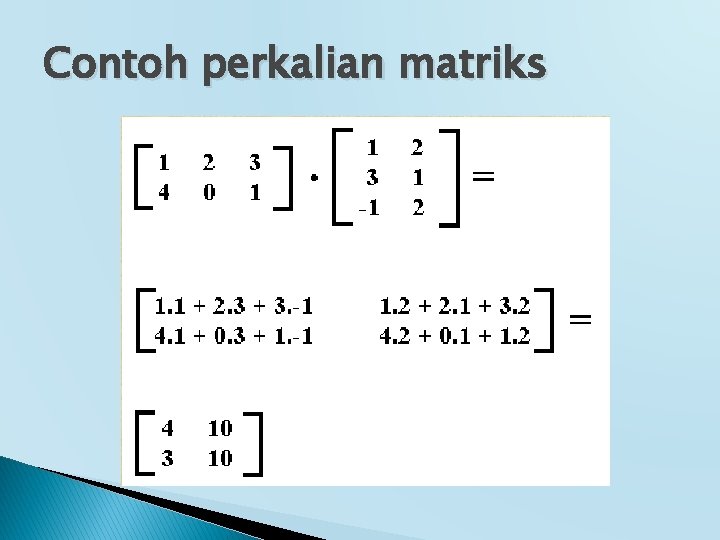
Contoh perkalian matriks

Contoh perkalian matriks � Matriks 2 x 2

Operasi Perkalian Matriks (1) � Diberikan matriks A (m x n) dan B (n x p)

Operasi perkalian matriks (2) Hasil kali A dan B adalah matriks C yang berukuran m x p dengan elemen-elemennya

Determinan matriks 2 x 2 � Diberikan matriks A (2 x 2) � Determinan A adalah

Bagaimana menghitung determinan matriks bujursangkar yang berukuran lebih besar dari 2 x 2 ?

Invers matriks � Matriks A (2 x 2) dikatakan mempunyai invers jika terdapat matriks B (2 x 2) sehingga AB = BA = I, dengan I matriks identitas. � Matriks B disebut invers matriks A. � Tidak setiap matriks mempunyai invers. Matriks yang mempunyai invers disebut matriks invertibel.

Menghitung invers matriks berukuran 2 x 2 (1) � Diberikan matriks A dan misalkan matriks B merupakan invers matriks A. Akibatnya

Rumus Invers Matriks

Contoh Invers Matriks � Diberikan � Invers matriks A berikut A adalah

Bagaimana menghitung invers matriks bujursangkar yang berukuran lebih besar dari 2 x 2 ?

Ruang Berdimensi 2 � Ruang berdimensi 2 merupakan kumpulan titik-titik (vektor) berikut � Anggota / elemen pada ruang berdimensi 2 disebut vektor dengan dua komponen.

Ruang Berdimensi 3 � Ruang berdimensi 3 merupakan kumpulan titik-titik berikut � Anggota / elemen pada ruang berdimensi 3 disebut vektor dengan tiga komponen.

Transformasi linear pada ruang dimensi 2 dan 3 Transformasi linear f adalah fungsi atau yang mempunyai sifat

Contoh transformasi linear pada ruang dimensi 2 �Pencerminan terhadap sumbu x �Proyeksi terhadap sumbu y �Rotasi sebesar 90 derajat berlawanan arah dengan jarum jam

Matriks representasi pencerminan terhadap sumbu x (1) � Diberikan fungsi berikut dengan definisi Namakan

Matriks representasi pencerminan terhadap sumbu x (2) � Pemetaan � Dapat tersebut dapat dinyatakan sebagai dicari bayangan titik P (2, 4) ketika dicerminkan terhadap sumbu x sbb :

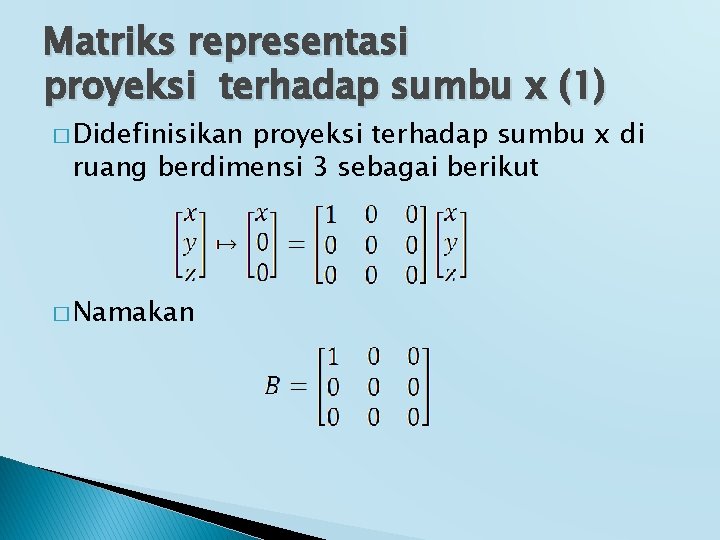
Matriks representasi proyeksi terhadap sumbu x (1) � Didefinisikan proyeksi terhadap sumbu x di ruang berdimensi 3 sebagai berikut � Namakan

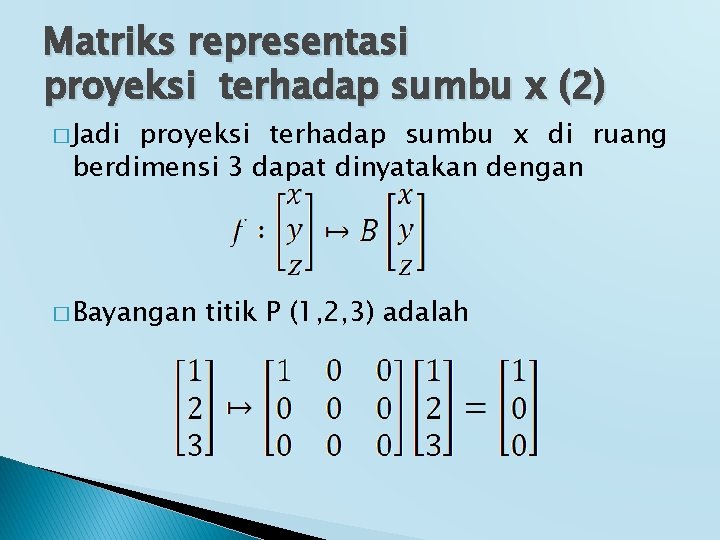
Matriks representasi proyeksi terhadap sumbu x (2) � Jadi proyeksi terhadap sumbu x di ruang berdimensi 3 dapat dinyatakan dengan � Bayangan titik P (1, 2, 3) adalah

matrices(utk Pertemuan 2). pdf

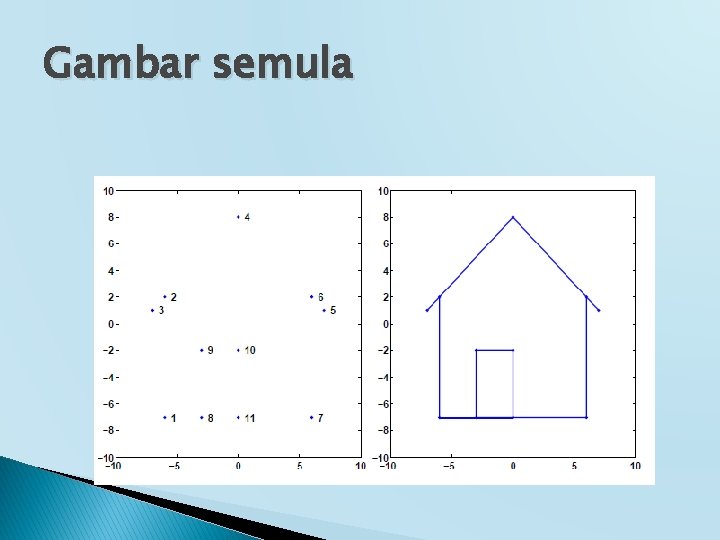
Gambar semula

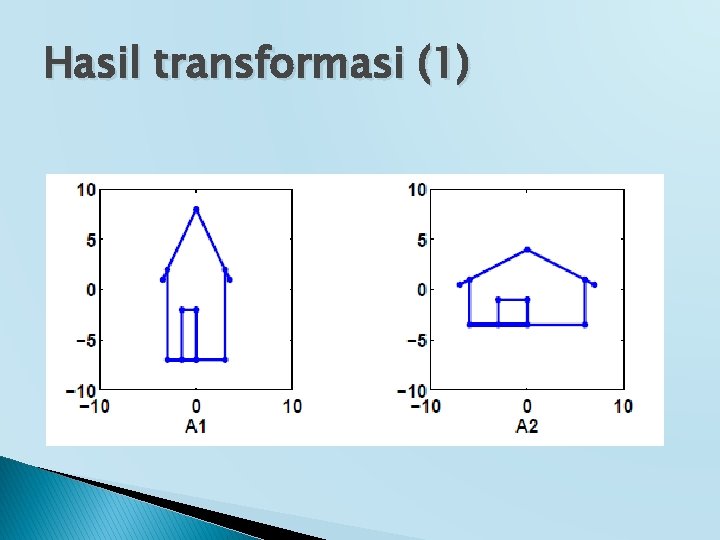
Hasil transformasi (1)

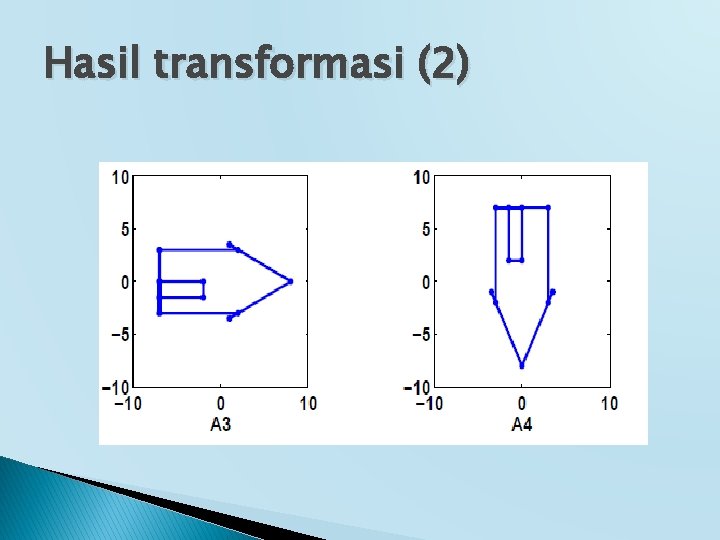
Hasil transformasi (2)

Hasil transformasi (3)

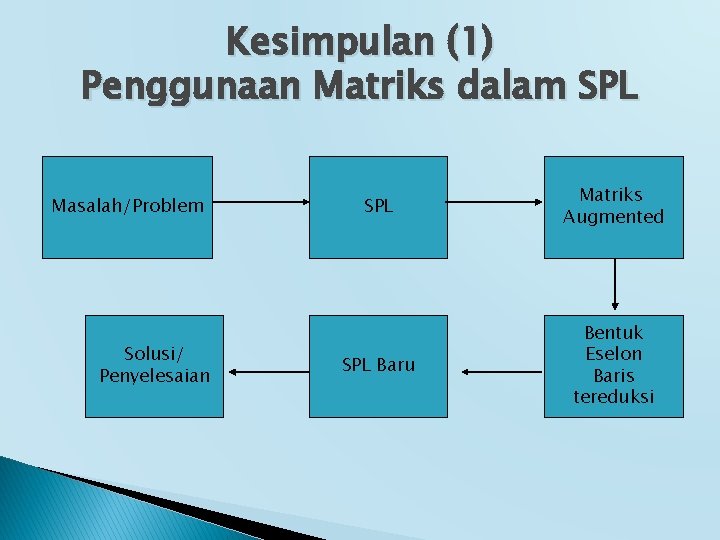
Kesimpulan (1) Penggunaan Matriks dalam SPL Masalah/Problem Solusi/ Penyelesaian SPL Matriks Augmented SPL Baru Bentuk Eselon Baris tereduksi

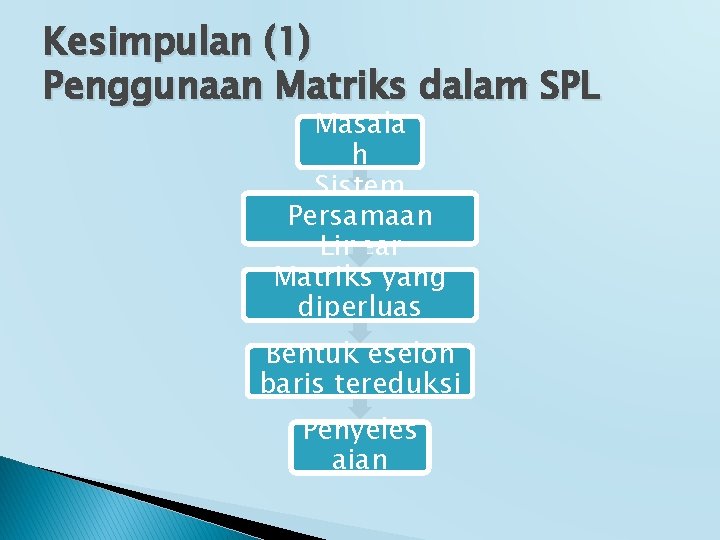
Kesimpulan (1) Penggunaan Matriks dalam SPL Masala h Sistem Persamaan Linear Matriks yang diperluas Bentuk eselon baris tereduksi Penyeles aian

Kesimpulan (2) Hubungan Transformasi Linear dan Matriks �Setiap transformasi linear dapat diwakili oleh suatu matriks. �Sebaliknya, suatu matriks dapat membangkitkan suatu transformasi linear