Pertemuan Ke 2 Array dan Matriks Struktur Data

Pertemuan Ke - 2 Array dan Matriks

Struktur Data : Array / Larik Tujuan Membahas struktur data yang paling sederhana dan mudah pengoperasiannya, yaitu array / larik. Definisi struktur data yang mengacu pada sekumpulan elemen yang diakses melalui indeks

KELEBIHAN & KEKURANGAN Array / Larik KELEBIHAN - Struktur Data paling mudah - Memori ekonomis, bila semua elemen terisi - Waktu akses sama ke setiap elemen KEKURANGAN - Boros memori jika banyak elemen yang tidak digunakan - Struktur Data Statis

PROSES LARIK Array / Larik Program Proses_Larik KAMUS Const Indeks A : N = 8 {jumlah elemen larik} : integer : array [1. . N] of integer ALGORITMA For Indeks 1 to N PROSES LARIK Endfor Catatan : {deklarasi larik A dengan tipe data integer} do Tipe Data sejenis (homogen) Indeks data memiliki keterurutan

CONTOH PROSES Array / Larik ALGORITMA For Indeks 1 to N PROSES LARIK Endfor Mengisi elemen larik dengan 0 (inisialisasi) Mengisi elemen larik dari piranti masukan Mencetak keluaran elemen larik ke piranti do

INISIALISASI Array / Larik ALGORITMA For Indeks 1 to 8 A[Indeks] = 0 Endfor 0 0 0 do 0 0 0

CETAK ELEMEN Array / Larik ALGORITMA For Indeks 1 to 8 Print A[Indeks] Endfor 2 7 4 9 5 3 1 1 3 5 7 2 9 4 do 7

PROSES BENTUK LAIN Array / Larik ALGORITMA For Indeks 1 to 8 Proses Larik Endfor do Mencari bilangan maksimun/minimum pada larik 5 7 1 3 2 9 4 7 Menjumlahkan nilai seluruh elemen larik Membuat rata-rata nilai seluruh elemen larik

Cari Bilangan Maksimum Array / Larik ALGORITMA Maks = A[1] For Indeks 2 to 8 do If A[Indeks] > Maks then Maks = A[Indeks] Endfor Print Maks 1 3 5 7 2 9 4 7

HITUNG PANJANG Array / Larik Panjang = UB - LB + 1 dimana: UB - upper bound ( indeks terbesar) LB - lower bound (indeks terkecil) Contoh : Seorang pedagang mobil menggunakan larik untuk menyimpan data penjualan dari tahun 1990 sampai dengan tahun 2001. Berapa panjang (jumlah elemen) larik yang harus disediakan? LB = 1990 UB = 2001 Jadi panjang = UB – LB + 1 = 2001 – 1990 + 1 = 12

PENGALAMATAN Array / Larik LOK(LA[K]) = Awal(LA) + W(K - LB) di mana: LOK(LA[K]) K Awal (LA) W LB – lokasi elemen dengan indeks K, yang dicari -- Indeks yang dicari -- Lokasi awal dari larik – jumlah byte untuk menyimpan 1 elemen larik -- lower bound / batas bawah

PENGALAMATAN Array / Larik LOK(LA[K]) = Awal(LA) + W(K - LB) Contoh: Misalkan Awal (Jual) = 100 dan W= 4, maka LOK (JUAL[1990]) = 100 LOK (JUAL[1991]) = 104 LOK (JUAL[1992]) = 108 Berapa lokasi JUAL[2000] ? untuk mendapat lokasi tersebut LOK(LA[K]) = Awal(LA) + W(K - LB) = 100 + 4 * (2000 – 1990) = 140

PENGALAMATAN Array / Larik Lokasi Memori Array Awal - 100 Jual(1990) 104 Jual(1991) 108 Jual(1992) 112 Jual(1993) 116 Jual(1994) 112 Jual(1995) 124 Jual(1996) 128 Jual(1997) 132 Jual(1998) 136 Jual(1999) 140 Jual(2000)

Kita lanjutkan untuk yang satu ini …. .

Struktur Data : Matriks Definisi • struktur data yang mengacu pada sekumpulan elemen yang diakses melalui indeks • Array dua dimensi, yang memiliki indeks baris dan kolom

KELEBIHAN & KEKURANGAN Matriks KELEBIHAN - Struktur Data paling mudah - Memori ekonomis, bila semua elemen terisi - Waktu akses sama ke setiap elemen KEKURANGAN - Boros memori jika banyak elemen yang tidak digunakan - Struktur Data Statis

Kamus Data Matriks KAMUS A : array [1. . 2, 1. . 3] of integer 2 x 3} Nilai {ukuran 50 x 4} {ukuran : array [1. . 50, 1. . 4] of real Type WAKTU : record < JJ : integer [0. . 23], MM : integer [0. . 59], DD : integer [0. . 59] > Catatan : Tipe Data sejenis (homogen) Absensi : array [1. . 100, 1. . 2] of Waktu Indeks data memiliki keterurutan

Proses Matriks Elemen Matriks diproses Baris demi Baris 2. Elemen Matriks diproses Kolom demi Kolom 1.

PROSES MATRIKS Matriks Program Proses_Matrik_Barisdemi. Baris KAMUS Const : M = 2 {jumlah baris matrik} Const : N = 3 {jumlah kolom array} Baris, Kolom : integer A : array [1. . M, 1. . N] of integer ALGORITMA For Baris 1 to M do For Kolom 1 to N do PROSES MATRIK Endfor

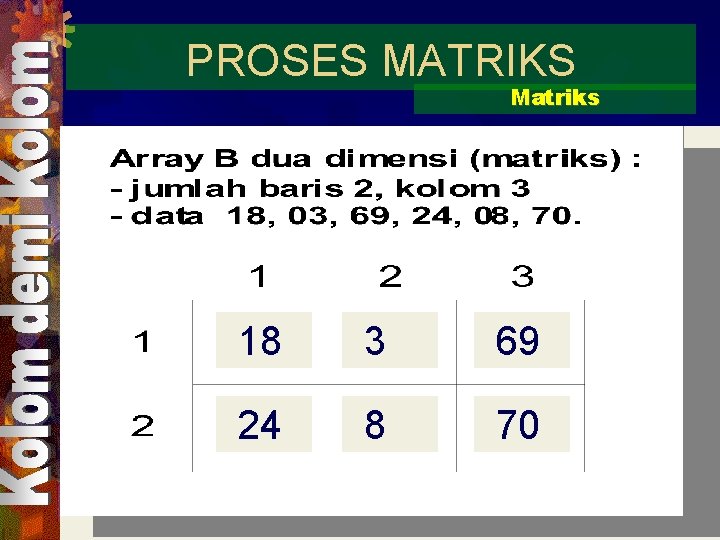
PROSES MATRIKS Matriks 18 3 69 24 8 70

PROSES MATRIKS Program Proses_Matrik_Kolomdemi. Kolom KAMUS Const : M = 2 {jumlah baris matrik} Const : N = 3 {jumlah kolom array} Baris, Kolom : integer A : array [1. . M, 1. . N] of integer ALGORITMA For Kolom 1 to N do For Baris 1 to M do PROSES MATRIK Endfor Matriks

PROSES MATRIKS Matriks 18 3 69 24 8 70

CONTOH PROSES ALGORITMA For Baris 1 to M do For Kolom 1 to N PROSES MATRIKS Endfor Mengisi elemen matriks dengan 0 (inisialisasi) Mengisi elemen matriks dari piranti masukan Mencetak keluaran elemen matriks ke piranti Matriks do

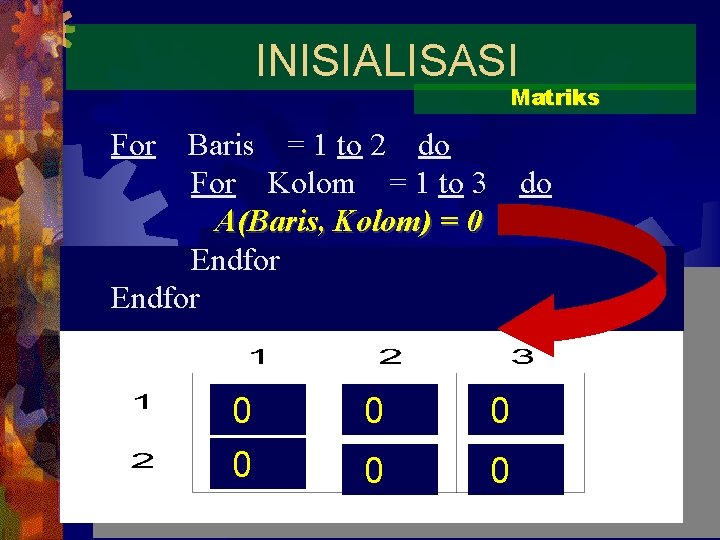
INISIALISASI Matriks For Baris = 1 to 2 do For Kolom = 1 to 3 A(Baris, Kolom) = 0 Endfor 0 0 do 0 0

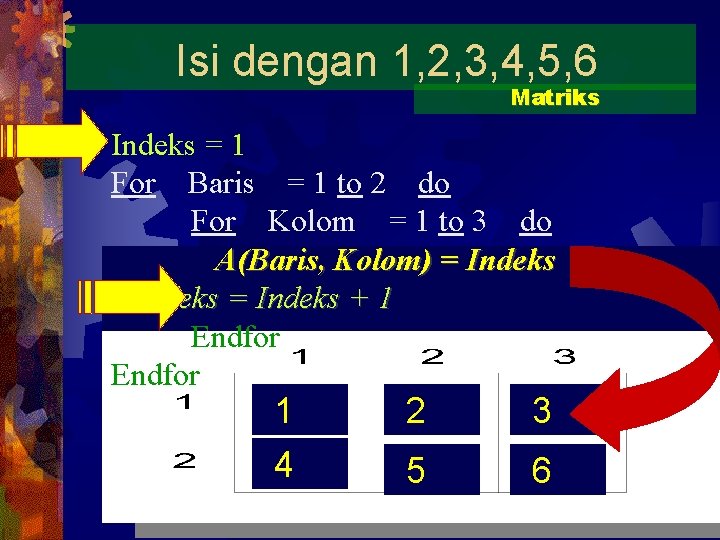
Isi dengan 1, 2, 3, 4, 5, 6 Matriks Indeks = 1 For Baris = 1 to 2 do For Kolom = 1 to 3 do A(Baris, Kolom) = Indeks + 1 Endfor 1 4 2 3 5 6

Isi dengan 1, 3, 5, 7, 9, 11 Matriks Indeks = ? ? ? For Baris = 1 to 2 do For Kolom = 1 to 3 do A(Baris, Kolom) = ? ? ? Indeks = ? ? ? Endfor 1 7 3 5 9 13

CETAK ELEMEN Matriks For 60 3 18 7 8 24 9 Baris = 1 to 2 do For Kolom = 1 to 3 A(Baris, Kolom) = 0 Endfor 18 24 3 69 8 70 do

PROSES LAINNYA Matriks For Baris = 1 to 2 do For Kolom = 1 to 3 do A(Baris, Kolom) = ? ? ? Endfor ROSES MATRIK DAPAT DIMODIFIKASI, sbb : Menjumlahkan nilai pada setiap baris Membuat rata-rata pada setiap baris atau setiap kolom

Menjumlahkan setiap baris Matriks For Baris = 1 to 2 do Total. Baris = 0 For Kolom = 1 to 3 do Total. Baris = Total. Baris + A[Baris, Kolom] Endfor Print Total Baris 18 Endfor 3 69 90 24 8 70 102

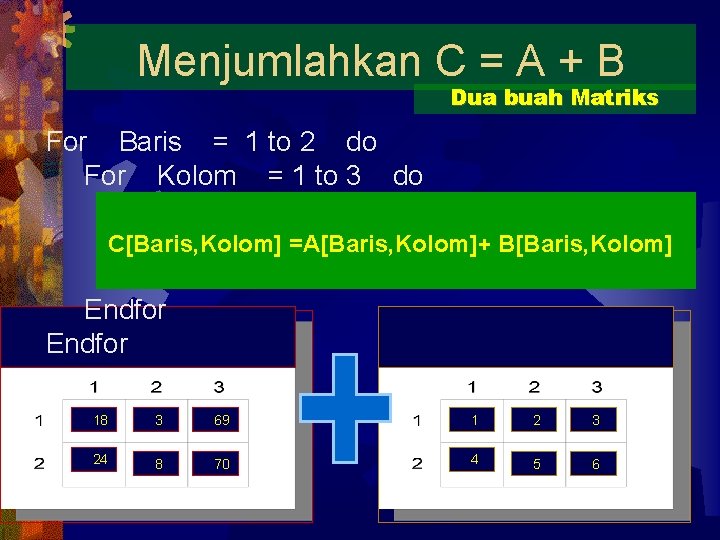
Menjumlahkan C = A + B Dua buah Matriks For Baris = 1 to 2 do For Kolom = 1 to 3 do C[Baris, Kolom] =A[Baris, Kolom]+ B[Baris, Kolom] Endfor 18 3 69 1 2 3 24 8 70 4 5 6

Mengalikan Matriks For Baris = 1 to 2 do For Kolom = 1 to 3 do C[Baris, Kolom] = 0 For K = 1 to P do C[Baris, Kolom] =C[Baris, Kolom]+ A[Baris, K] * B[K, Kolom] Endfor 18 3 69 24 8 70