Pertemuan 7 stack Struktur Data Majemuk Linear Stack

Pertemuan 7 stack

Struktur Data Majemuk �Linear � Stack, Queue, List �Non Linear � Tree, Graph

Stack �Definisi Stack �Operasi-operasi dasar Stack � Push � Pop

STACK (TUMPUKAN) �Kumpulan items yang teratur dimana items baru akan dimasukkan ke dan sebuah items akan dikeluarkan dari satu ujung yang sama, yaitu dari TOP sebuah stack. �Struktur data linier dimana hanya bagian TOPnya saja yang bisa diakses. �Bersifat LIFO = Last In First Out. �Bisa diimplementasikan menggunakan array atau Linked List.

Last In First Out

Penggunan Stack �History pada web browser. �Undo Log pada text editor. �Pemrosesan struktur bersarang (nested) : loop, rekursi, fungsi, dll. �Algoritma back tracking – Artificial Intelegence

Operasi Dasar Stack �Push : memasukkan sebuah item baru ke dalam stack. �Pop : mengeluarkan sebuah item dari stack. �Operasi lain : Is_Empty, Is_Full Note : pop dan push dilakukan melalui ujung yang sama (TOP)

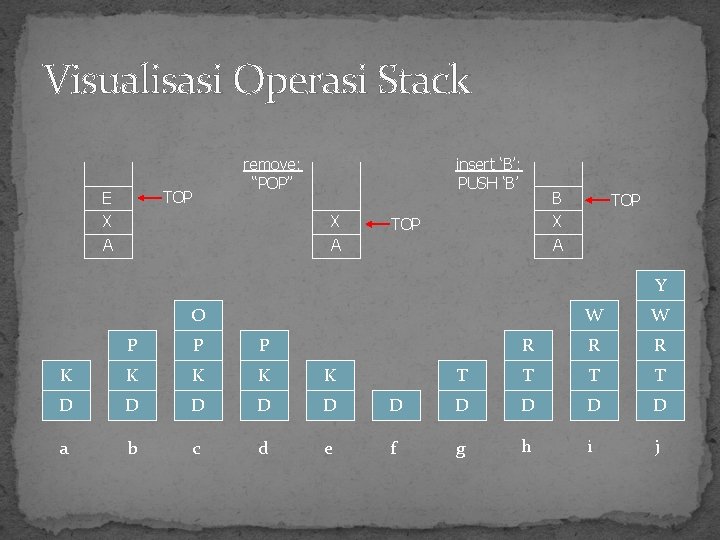
Visualisasi Operasi Stack TOP E X A remove: “POP” insert ‘B’: PUSH ‘B’ X A B X A TOP Y O W W R R R T T P P P K K K D D D D D a b c d e f g h i j

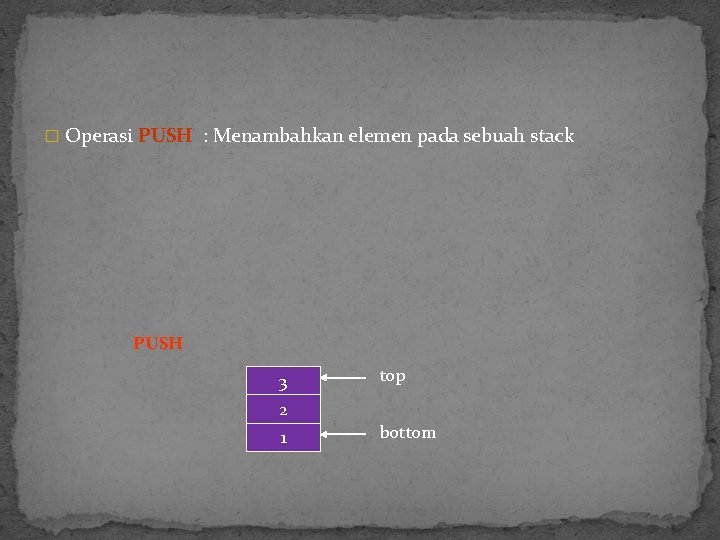
Push � Operasi PUSH : Menambahkan elemen pada sebuah stack PUSH 1 top== bottom

PUSH � Operasi PUSH : Menambahkan elemen pada sebuah stack PUSH 2 1 top bottom

� Operasi PUSH : Menambahkan elemen pada sebuah stack PUSH 3 top 2 1 bottom

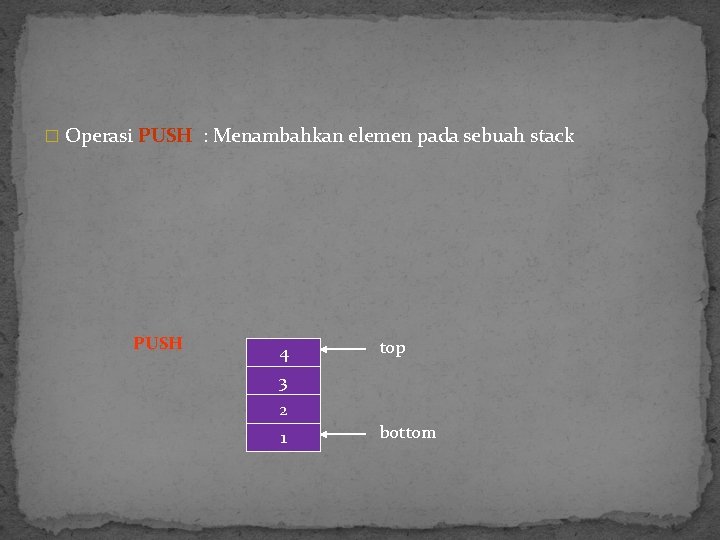
� Operasi PUSH : Menambahkan elemen pada sebuah stack PUSH 4 top 3 2 1 bottom

Pop � Operasi POP : Menghapus sebuah elemen dari sebuah stack 6 POP top 5 4 3 2 1 bottom

� Operasi POP : Menghapus sebuah elemen dari sebuah stack POP 5 top 4 3 2 1 bottom

� Operasi POP : Menghapus sebuah elemen dari sebuah stack POP 3 top 2 1 bottom

� Penambahan dan penghapusan elemen dilakukan pada elemen list yang terletak di paling depan � Yang dihapus adalah elemen yang paling terakhir ditambahkan � Nama lain： LIFO (Last In First Out) � Operasi POP : Menghapus sebuah elemen dari sebuah stack 16

Langkah Membuat Stack Membuat struktur data class Mendefinisikan atribut class. Membuat fungsi/ operasi method 1. 2. 3. 1. 2. 4. Push Pop. Membuat fungsi utama main()

Deklarasi Struktur Data Stack #define maxsize 100 // mendefinisikan maks ukuran data // dlm stack typedef struct { int top; // indeks TOP char items [ maxsize ] // array } stack; // nama tipe data baru yg dibuat // adalah stack

Deklarasi Fungsi-Fungsi Stack �void initialize ( stack *s) �void pop ( stack *s, char *x ) �void push ( stack *s, char x ) �void show ( stack *s )

Fungsi Initialize void initialize ( stack *s) // operasi initialize dg parameter // s bertipe pointer stack { s -> top = -1; // top = -1 stack dlm kondisi empty }

Fungsi Push void push ( stack *s, char x ) { if (s->top > maxsize) // stack is full printf("n. ERROR: the stack is full!"); else { s->top = s->top + 1; s->items [ s->top ] = x; printf("n. PUSH SUCCEED"); } }

Fungsi Pop void pop ( stack *s, char *x ) { if (s->top < 0) // stack is empty printf("n. ERROR: the stack is empty!"); else { *x = (s->items [ s->top ]); s->top = s->top - 1; printf("n. POP SUCCEED"); } }

Fungsi Show void show( stack *s ) { printf("n. ISI STACK : n"); for(int i=s->top; i>=0; i--) printf("t%cn", s->items[i]); printf("n"); }

Fungsi Main void main() { stack *my_stack, s; char item, *x; my_stack = &s; x = &item; initialize(my_stack); push(my_stack, 'A'); push(my_stack, 'R'); push(my_stack, 'I'); push(my_stack, 'F'); show(my_stack); pop(my_stack, x); show(my_stack); }

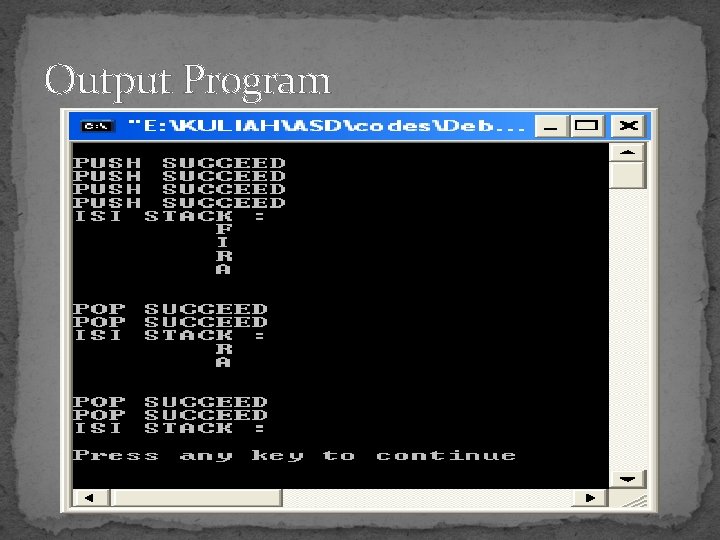
Output Program

Stack – Linked List �Jika sebuah linked list SELALU menambahkan node baru dan menghapus node lama dari salah SATU ujungnya saja (posisi Head ataukah Tail) STACK. �TOP = head untuk single linked list. �TOP = tail untuk double linked list. �HOW?

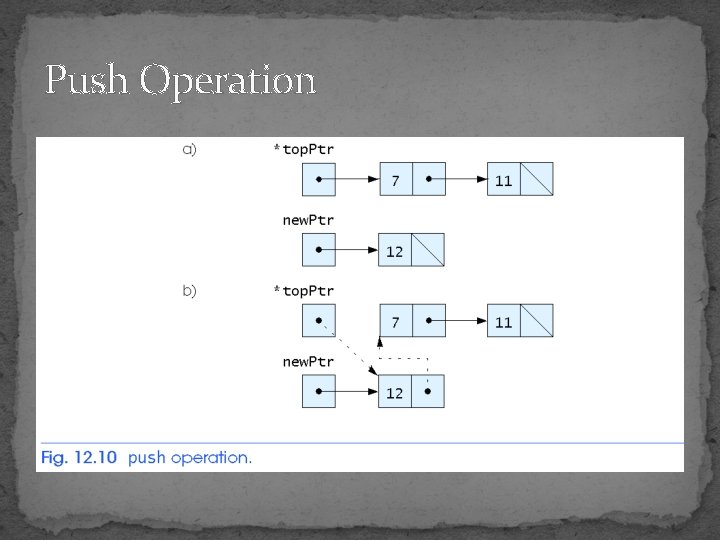
Push Operation

Pop Operation

Apakah Tanda Kurungnya Valid? {x+(y-[a+b])*c-[(d+e)]}{z+(y [d+f]}*g-((d+h)]}{w+(y[a+r])*j-[(k+e)]}

Pengecekan Tanda Kurung valid = true s = the_empty_stack while ( we_have_not_read_the_entire_string ) { read the next symbol (symb) of the string if ( symb == ‘(‘ || symb == ‘[‘ || symb == ‘{‘ ) //apakah symb termasuk kurung buka? push ( s, symb ) // jika symb adalah kurung buka if ( symb == ‘)‘ || symb == ‘]‘ || symb == ‘}‘ ) //apakah symb termasuk kurung tutup? if ( empty ( s ) ) valid = false else { k = pop ( s ); if ( k is_not_the_matching_opener_of_symb ) valid = false } // end else } // end while if ( ! empty ( s ) ) valid = false if ( valid ) output ( “the string is valid” ) else output ( “the string is not valid” );

Example Case 1. 2. 3. Cek apakah string di bawah ini valid! (a+b)} (h-(j-(k-[l-n])) {x+(y-[a+b])*c-[(d+e)]} Valid

Evaluasi Postfix �Postfix adalah bentuk persamaan matematika dimana operator ditulis setelah kedua operannya. �Contoh : � AB+ � CDE*- C-(D*E) � FG/H+ (F/G)+H �Latihan : Ubah infix ke postfix � {([(A+B)*C] – (D – E))^(F+G)} � AB+C*DE - - FG+^

Algoritma Evaluasi Postfix opndstck = the_empty_stack /* scan the input string, one by one element, into symb while ( not_end_of_input_string ) { symb = next_input_character if ( symb_is_an_operand ) push ( opndstck, symb ) else /* symb is an operator */ { opnd 2 = pop ( opndstck ) opnd 1 = pop ( opndstck ) value = opnd 1 (symb) opnd 2 push ( opndstck, value ) } /* end else */ } /* end while */ return ( pop ( opndstck ) )

SOAL POSTFIX : Jika A = 4, B = 2, C = 3, hitunglah : 1. ABC+–ACB^*+ 2. AB*CB+^AC+–