Pertemuan 7 KETIDAKPASTIAN Betha Nurina Sari M Kom

Pertemuan 7 KETIDAKPASTIAN Betha Nurina Sari, M. Kom

KETIDAKPASTIAN Probabilitas Teorema Bayes Faktor Kepastian (Certainty Factor) Latihan Soal

KETIDAKPASTIAN • Ketidakpastian dapat dianggap sebagai suatu kekurangan informasi yang memadai untuk membuat suatu keputusan. • Ketidakpastian merupakan suatu permasalahan karena mungkin menghalangi kita membuat suatu keputusan yang terbaik.

KETIDAKPASTIAN • Banyak masalah tidak dapat dimodelkan secara lengkap dan konsisten. • Misalnya : – Suatu penalaran dimana adanya penambahan fakta baru mengakibatkan ketidakkonsistenan, – dengan ciri-ciri sebagai berikut : • - adanya ketidakpastian • - adanya perubahan pada pengetahuan • - adanya penambahan fakta baru dapat mengubah konklusi yang sudah terbentuk

KETIDAKPASTIAN Contoh : • Premis -1 : Aljabar adalah pelajaran yang sulit • Premis -2 : Geometri adalah pelajaran yang sulit • Premis -3 : Kalkulus adalah pelajaran yang sulit • Konklusi : Matematika adalah pelajaran yang sulit

KETIDAKPASTIAN • Munculnya premis baru bisa mengakibatkan gugurnya konklusi yang sudah diperoleh, misal : • Premis -4 : Kinematika adalah pelajaran yang sulit • Premis tersebut menyebabkan konklusi : “Matematika adalah pelajaran yang sulit”, menjadi salah, karena Kinematika bukan merupakan bagian dari Matematika, sehingga bila menggunakan penalaran induktif sangat dimungkinkan adanya ketidakpastian.

PROBABILITAS • Probabilitas menunjukkan kemungkinan sesuatu akan terjadi atau tidak. • P(E) = jumlah kejadian berhasil/ jumlah semua kejadian • Misal dari 10 orang sarjana , 3 orang menguasai CISCO, sehingga peluang untuk memilih sarjana yang menguasai CISCO adalah : • p(CISCO) = 3/10 = 0. 3

PROBABILITAS • P(E) = 0 -> Peristiwa E pasti tidak terjadi • P(E) = 1 -> Peristiwa E pasti terjadi • Apabila E bukan peristiwa E, maka P(E) = 1 - P(E) Atau berlaku P(E) + P(E) =1

PROBABILITAS KONDISIONAL

TEOREMA BAYES

Contoh Penerapan Teorema Bayes • Diketahui : • P(demam)=0, 4. P (muntah) = 0, 3. P(demam|muntah)=0, 75 • Berapa nilai P(muntah|demam) ?

TEOREMA BAYES • Kegunaan menentukan probabilitas diagnostik dari probabilitas kausal: – P(Cause|Effect) = P(Effect|Cause) P(Cause) / P(Effect) – Contoh: m adalah meningitis, s adalah sakit leher: – P(m) = 0. 0001. P(s) = 0. 1 dan P (s|m)=0. 8. P(m|s) = P(s|m) P(m) / P(s) = 0. 8 × 0. 0001 / 0. 1 = 0. 0008

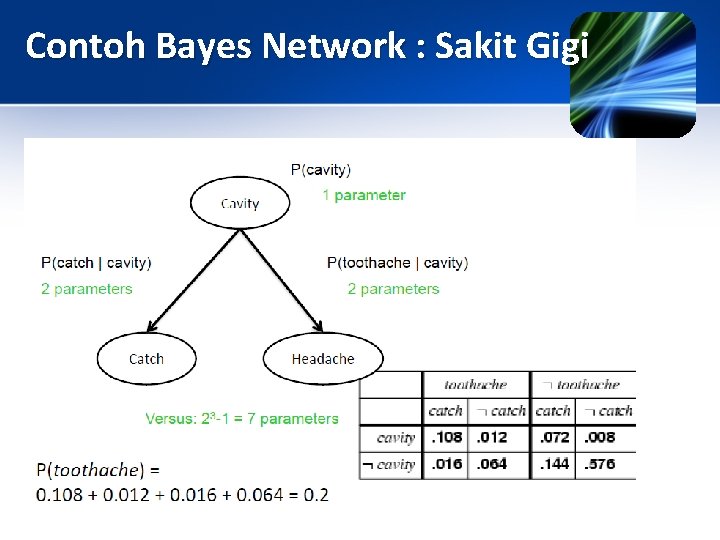
Contoh Bayes Network : Sakit Gigi

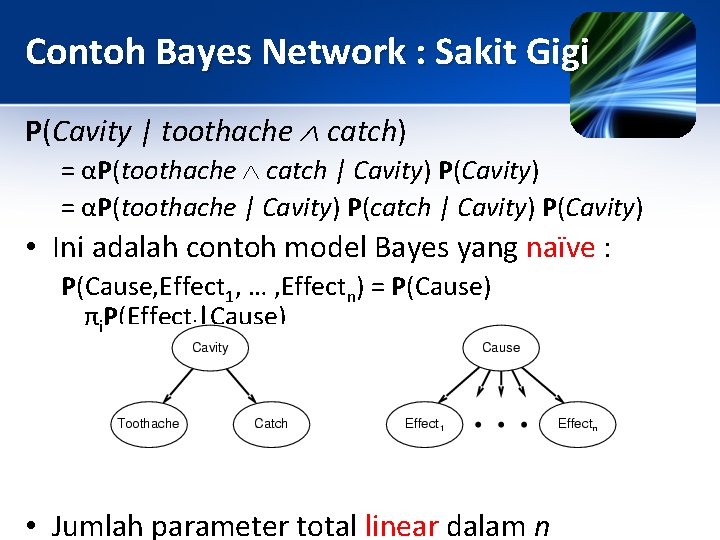
Contoh Bayes Network : Sakit Gigi P(Cavity | toothache catch) = αP(toothache catch | Cavity) P(Cavity) = αP(toothache | Cavity) P(catch | Cavity) P(Cavity) • Ini adalah contoh model Bayes yang naïve : P(Cause, Effect 1, … , Effectn) = P(Cause) πi. P(Effecti|Cause) • Jumlah parameter total linear dalam n

FAKTOR KEPASTIAN (CERTAINTY FACTOR) • Penggabungan kepercayaan dan ketidakpercayaan dalam bilangan yang tunggal memiliki dua kegunaan, yaitu : • Faktor kepastian digunakan untuk tingkat hipotesis di dalam urutan kepentingan. • Contoh : jika seorang pasien mempunyai gejala tertentu yang mengindikasikan beberapa kemungkinan penyakit, maka penyakit dengan CF tertinggi menjadi urutan pertama dalam urutan pengujian.

FAKTOR KEPASTIAN (CERTAINTY FACTOR)

Contoh • Probabilitas seorang menderita tuberkulosis = 0. 02. Dari data observasi didapatkan bahwa dari 100 penderita TB, 40 memiliki gejala kanker paru -paru (KP). • Hitung faktor kepastian bahwa TB disebabkan kanker paru-paru? • P(TB) = 0. 02 • P(TB|KP) = 40/100 = 0. 4

Contoh

Latihan Soal 1. Peluang seorang lelaki yg telah menikah menonton suatu acara di tv adalah 0. 4 dan peluang seorang wanita yg telah menikah menonton acara TV yang sama 0. 5. Peluang seorang lelaki menoton acara TV tsb bila istrinya menonton adalah 0. 7. Hitunglah : a. Peluang sepasang suami istri menonton acara TV tsb b. Peluang seorang istri menonton acara TV itu bila suaminya menonton acara TV tsb c. Peluang paling sedikit seorang dari sepasang suami istri menonton acara TV yang sama

Latihan Soal • Selama beberapa tahun terakhir, diketahui bahwa perkantoran itu menggunakan listrik PLN adalah 0. 9 dan peluang menggunakan generator adalah 0. 1, peluang terjadi ketidakstabilan pada arus PLN 0, 2 dan peluang terjadi ketidakstabilan pada generator 0. 3. • Bila suatu saat diketahui terjadi ketidakstabilan arus listrik, maka berapakah probabilitas saat itu aliran listrik berasal dari generator?

3. Pada awal tahun 2015, rekrutmen personil berkualifikasi tinggi hanya terbuka untuk mahasiswa dari tiga universitas: Universitas Laval, Universitas Montreal dan Concordia University. Informasinya adalah sebagai berikut : • Tingkat keberhasilan pelamar dari Laval University : 85%; • Tingkat keberhasilan pelamar dari Universitas Montreal : 80%; • Tingkat keberhasilan pelamar dari Concordia University : 90%; • Tingkat keberhasilan untuk semua calon adalah 82%. • Kami berasumsi bahwa hasil kompetisi tahun 2015 adalah perkiraan yang baik dari orang-orang dari tahun berikutnya. Selain itu, kita mengasumsikan bahwa proporsi siswa dari University of Montreal di kompetisi ini adalah dua kali lipat dari Laval University. • a) Buatlah pohon peristiwa/pohon keadaan. (Pastikan untuk menentukan peristiwa dan probabilitas terkait. )

Latihan Soal • b) Tentukan proporsi mahasiswa dari tiga universitas (Laval, Montreal dan Concordia) untuk masuk kompetisi pada tahun 2003. • c) Jika kita tahu bahwa seorang mahasiswa pelamar tidak lulus ujian, tentukan probabilitas bahwa ia datang dari Concordia University.

Persiapan UTS > Pekan Depan • Bahan Materi Pertemuan 1 -7 • UTS bersifat open Note : – Silakan membuat Ringkasan di kertas A 4 (1 lembar/2 halaman bolak-balik) – Boleh tulis tangan atau print ketik