PERTEMUAN 5 1 MATRIKS 2 METODE ELIMINASI GAUSS

PERTEMUAN 5 1. MATRIKS 2. METODE ELIMINASI GAUSS 3. METODE ITERASI GAUSS SEIDEL 4. METODE DEKOMPOSISI LU

MATRIKS Definisi Matriks Adalah kumpulan bilangan yang disajikan secara teratur dalam baris dan kolom.

Notasi Matriks A = -- a 11 a 12 …. a 1 n a 21 a 22 …. a 2 n . . am 1 am 2 …. amn

Ukuran Matrik atau Ordo Matrik A adalah mxn dimana : m = banyak baris n = banyak kolom Elemen matrik aij artinya elemen baris ke-I dan kolom ke-j pada matrik A

Jenis-jenis matriks 1. Vektor adalah matriks yang hanya mempunyai satu baris dan satu kolom - jika matriks [A] hanya mempunyai satu baris maka disebut vektor baris 2. Matriks bujur sangkar bila ordo A adalah m x n dimana m = n 3. Matriks Nol adalah matriks yang elemennya nol 4. Matriks diagonal adalah matriks yang hanya elemen diagonal tidak sama dengan nol 5. Matriks Identitas adalah bentuk khusus dari matriks diagonal dimana elemen-elemen diagonalnya sama dengan nol

6. Matriks segitiga adalah suatu matriks persegi dikatakan sebagai matriks segitiga jika elemen yang ada di bawah atau di atas diagonal utamanya (salah satu, tidak kedua-duanya) bernilai nol. Jika elemen-elemen yangada di bawah diagonal utama bernilai nol maka disebut sebagai matriks segitiga atas. Sebaliknya, jika elemen-elemen yang ada di atas diagonal utamanya bernilai nol maka disebut sebagai matriks segitiga bawah.

Penambahan matriks Sesuatu matriks boleh ditambah jika kedua matriks mempunyai susunan yang sama. Begitu juga dengan pengurangan matriks,

Contoh 1 penambahan matriks:

Contoh 2 Pengurangan Matriks

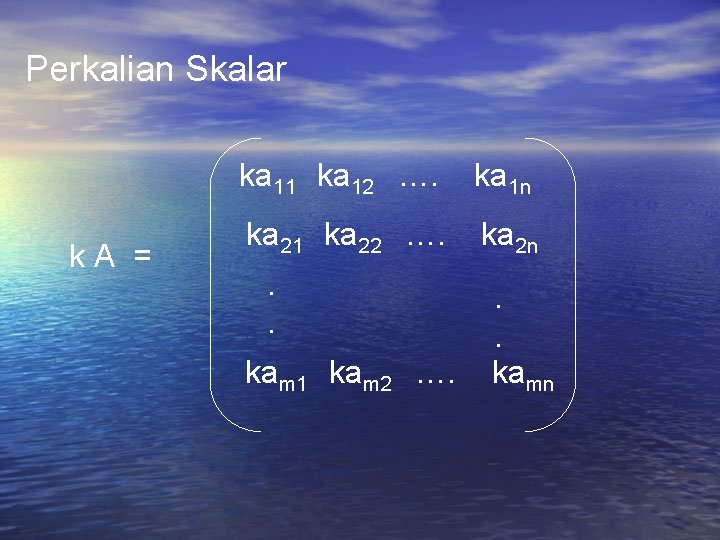
Perkalian Skalar k. A = ka 11 ka 12 …. ka 1 n ka 21 ka 22 …. ka 2 n . . kam 1 kam 2 …. . . kamn

Contoh 3 perkalian skalar

Perkalian matriks dengan matriks Dua buah matriks A(m x n) dan B(n x k) dapat dikalikan apabila memenuhi syarat: • Jika dan hanya jika jumlah kolom matrik A sama dengan jumlah baris matriks B • Ordo matriks hasil perkalian A dan B adalah ( m x k )

Contoh 4 perkalian matriks dengan matriks

Contoh 4

Determinan Matriks Jika suatu matriks adalah matriks bujur sangkar maka mempunyai nilai determinannya Determinan matriks A di dinotasikan dengan | A | Cara menghitung determinan tergantung ordo matriks tersebut

Determinan matriks ordo 2 x 2 a 11 a 12 a 21 a 22 A= det. A = |A| = a 11 a 22 - a 21 a 12

Determinan matriks ordo 3 x 3 A= a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

Determinan matrik A ( 3 x 3 menggunakan metode SARRUS: ) dihitung | A | = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 - a 31 a 22 a 13 - a 32 a 23 a 11 - a 33 a 21 a 12

Contoh 5 determinan Matriks 2 x 2

Contoh 5 Matriks 3 x 3

Matriks Invers Sebuah matriks A dikatakan mempunyai invers apabila matriks A adalah matriks Non singular, yaitu matriks bujur sangkar yang determinannya tidak sama dengan nol, ditulis dengan A- 1 sehingga berlaku: A-1 A = A A-1 = I dimana I adalah matriks identitas

Menentukan matriks invers Menggunakan metode Adjoin: A- 1 = Adjoin A Det. A

Adjoin A adalah transpose dari matrik kofaktor -kofaktor dari matrik A Adjoin A = A 11 A 12. . A 1 n . . . An 1 An 2. . Ann

Ai j adalah kofaktor dari elemen ai j dimana : Ai j = ( - 1 )i+ j | Mi j adalah submatrik dari A yang diperoleh dengan jalan menghilangkan baris ke – i dan kolom ke – j pada A

Contoh 6 Matriks invers

Contoh 6

KESAMAAN MATRIKS Dua matriks adalah sama jika mempunyai susunan yang sama dan unsur sepadan yang sama. Contoh 7:

Metode Eliminasi Gauss yaitu menghilangkan atau mengurangi jumlah variable sehingga dapat diperoleh nilai dari suatu variable bebas matrik diubah menjadi augmented matrik :

Metode Eliminasi Gauss ubah matrik menjadi matrik segitiga atas atau segitiga bawah dengan menggunakan OBE (Operasi Baris Elementer).

Metode Eliminasi Gauss Sehingga penyelesaian dapat diperoleh dengan:

Contoh 1: Selesaikan sistem persamaan berikut: Augmented matrik dari persamaan linier simultan tersebut :

Contoh 1 : Lakukan operasi baris elementer

Contoh 1: Penyelesaian :

Algoritma Eliminasi Gauss

Algoritma Eliminasi Gauss

Metode Iterasi Gauss-Seidel Metode interasi Gauss-Seidel adalah metode yang menggunakan proses iterasi hingga diperoleh nilai yang berubah. Bila diketahui persamaan linier simultan

Metode Iterasi Gauss-Seidel Berikan nilai awal dari setiap xi (i=1 s/d n) kemudian persamaan linier simultan diatas dituliskan menjadi:

Metode Iterasi Gauss. Seidel Dengan menghitung nilai-nilai xi (i=1 s/d n) menggunakan persamaan-persamaan di atas secara terus-menerus hingga nilai untuk setiap xi (i=1 s/d n) sudah sama dengan nilai xi pada iterasi sebelumnya maka diperoleh penyelesaian dari persamaan linier simultan tersebut. Atau dengan kata lain proses iterasi dihentikan bila selisih nilai xi (i=1 s/d n) dengan nilai xi pada iterasi sebelumnya kurang dari nilai tolerasi error yang ditentukan. Untuk mengecek kekonvergenan

Contoh 1: Jawab :

Contoh 1 Nilai iterasi ke-7 sudah tidak berbeda jauh dengan nilai iterasi ke-6 Maka proses dihentikan diperoleh penyelesaian:

Algoritma Eliminasi Gauss Seidell

Alogoritma Eliminasi Gauss Seidell

Metode Dekomposisi LU Jika matriks A non singular ( matriks yang mempunyai invers ), maka ia dapat difaktorkan ( diuraikan atau dikekomposisi ) menjadi matriks segitiga bawah, L (Lower) dan matriks segitiga atas, U (Upper) dengan cara melakukan sejumlah transformasi elementer pada baris seperti contoh sebelumnya, A = LU.

Perubahan tersebut dapat digambarkan sebagai berikut A Transf. elementer pada baris U L

Pada matriks segitiga bawah, L, semua elemen diagonal utamanya berharga 1, sedangkan pada matriks segitiga atas, U tidak ada aturan khusus pada elemen diagonal utamanya. Setelah pemfaktoran matriks A menjadi matriks L dan matriks U, maka kedua matriks tersebut dapat digunakan untuk menyelesaikan sistem persamaan linier AX = B, yaitu sebagai berikut. Tinjau SPL AX = B, kemudian faktorkan A menjadi L dan U, sehingga A = LU, sehingga LUX = B. Misalkan UX = y, maka Ly = B. Untuk memperoleh , kita gunakan teknik substitusi maju ( forward substitution ), sbb,

Dan untuk memperoleh solusi SPL, , kita gunakan teknik substitusi mundur ( back substitution ) sbb,

Contoh 1 Tentukan X 1, X 2, X 3 dan X 4 dari sistem persamaan linier di bawah ini dengan metode dekomposisi LU

CONTOH 1

CONTOH 1

CONTOH 1

CONTOH 1

Algoritma Metode Dekomposisi LU 1. Mendapatkan matriks [L] dan [U]. 2. Menyelesaikan [L]{z} = (b). 3. Menyelesaikan [U]{x} = {z}

Soal : 1. Selesaikan persamaan berikut dengan metode Eliminasi Gauss

Soal : 2. Selesaikan persamaan berikut dengan metode Eliminasi Gauss Seidell

Soal : 3. Selesaikan matriks berikut dengan metode Dekomposisi LU