Perspective Transformation 3 D Imaging Transformation o A

Perspective Transformation

3 -D Imaging Transformation: o A 3 D projection is a mathematical transformation used to project three Dimensional points onto a two Dimensional plane. o Often this is done to simulate the relationship of the camera to subject. o 3 D projection is often the first step in the process of representing three dimensional shapes, two dimensionally in computer graphics, a process known as rendering.

3 -D Imaging Transformation: o There are two basic ways for projecting 3 -D objects onto a 2 D plane. 1. Parallel Projection. 2. Perspective Projection. o Projections transform points in n -space to m -space, where m < n. In 3 D, we map points from 3 -space to the projection plane (PP)

Perspective Transformation. o When human eyes see near things they look bigger as compare to those which are far away. This is called perspective in a general way. Whereas transformation is the transfer of an object e. t. c from one state to another. o So overall, the perspective transformation deals with the conversion of 3 d world into 2 d image. The same principle on which human vision works and the same principle on which the camera works.

Vanishing Point (Perspective Projecion)

Perspective vs. parallel projections

Parallel projections

Frame of reference o. Frame of reference is basically a set of values in relation to which we measure something.

5 Frames of Reference

Mathematical Explanation

Calculating the size of image formed o. Suppose an image has been taken of a tree 5 m tall, at a distance of 50 m from the camera, and we have to tell that what is the size of the image of the tree, with a camera of focal length is 50 mm.

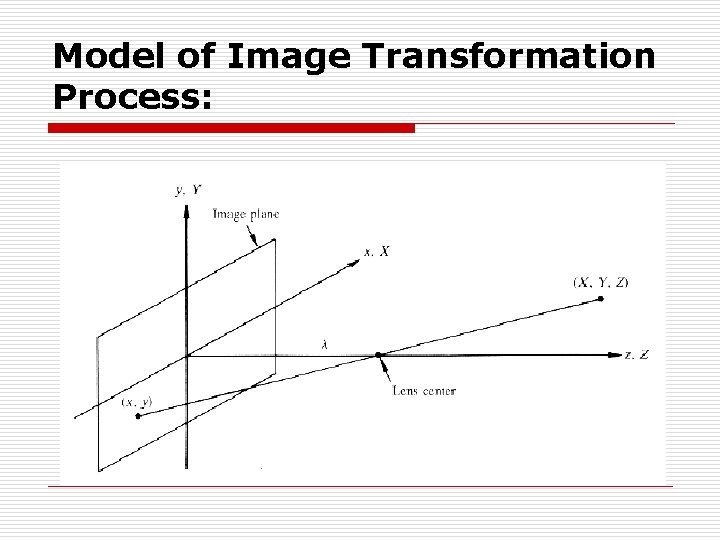
Model of Image Transformation Process:

Perspective Projection: o A perspective transformation (Imaging transformation) projects 3 -D points onto a 2 -D plane. o Lets assume that, the camera co-ordinate system (x, y, z) has the image plane coincident with the xy-plane and the optical axis (established by the center of lens) along the z-axis. o Thus the center of Image Plane is at the Origin. o For Projection, there are two possible scenarios, including: n n When the Origin is at the Lens Center. When the Origin is moved to the center of Image plane.

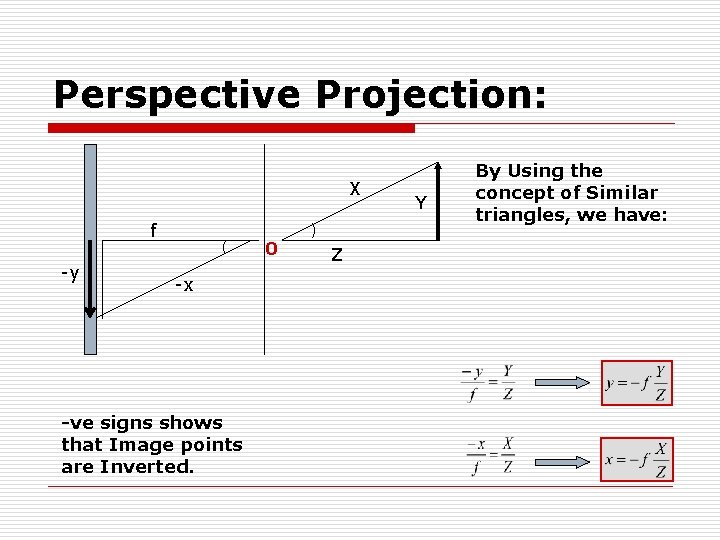
Perspective Projection: 1. Origin at lens center: Lens 3 D world (X, Y, Z) f ( Pin hole camera Image plane y O ) Z

Perspective Projection: X f -y ( -x -ve signs shows that Image points are Inverted. 0 ) Z Y By Using the concept of Similar triangles, we have:

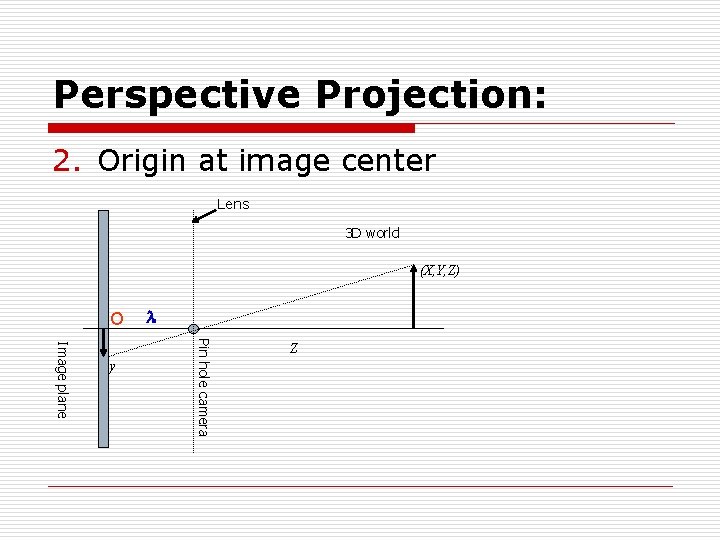
Perspective Projection: o Now , if the Origin is moved to the center of Image plane, then the center of the lens is located at coordinates (0, 0, ). o If the camera is in focus for distant objects, is the focal length of the lens.

Perspective Projection: 2. Origin at image center Lens 3 D world (X, Y, Z) O Pin hole camera Image plane y Z

Perspective Projection: X 0 -y ) ( Z- -x Z -ve signs shows that Image points are Inverted. Y By Using the concept of Similar triangles, we have:

Perspective Projection: o Thus we have projected a 3 -D object on 2 -D Image plane, and it is given by: (x , y)= ( , ) o These equations are Non Linear due to division by Z. o Remember that, the third dimension is lost during Image formation! o It does play an Impact during Image formation, as (x, y) are dependent upon “Z”

Homogeneous Transform: o To represent the (x, y) in Linear matrix form, we may use the concept of Homogeneous coordinates. o Homogeneous coordinates of a point (X, Y, Z) are given as ( k. X, k. Y, k. Z, k ) where k is an arbitrary non-zero constant. Cartesian World coordinate in Homogenous form

Inverse Homogeneous Transform: o The Inverse homogeneous transform converts homogenous coordinates back into Cartesian coordinates. n (Ch 1, ch 2, ch 3) = (ch 1/ch 4, ch 2/ch 4, ch 3/ch 4) n (X, Y, Z) (KX/K, KY/K, KZ/K) = World coordinate in Homogenous form World coordinate

Perspective Projection using Homogeneous coordinates: o The Transformation matrix for “Perspection” is denoted by P and given by:

Perspective Projection using Homogeneous coordinates: o Then the product P*Wh Ch = P yields a vector denoted by Ch. * Wh Ch represents the Camera co ordinate in Homogeneous form.

Perspective Projection using Homogeneous coordinates: Ch represents the Camera co ordinate in Homogeneous form.

Perspective Projection using Homogeneous coordinates: o The elements of Ch are the camera coordinates in homogeneous form. o Dividing first three components Ch of by fourth can form Cartesian coordinates. o Therefore in Cartesian form

Perspective Projection using Homogeneous coordinates: o o The third component is of no interest as it is lost while projection on image plane. And

Inverse Perspective Projection: o The Inverse Perspective transformation can be used to map an Image point back into 3 D space. As Ch=P Wh o As Wh=P-1 Ch The Inverse Perspective Transformation Matrix is given by: P-1= 1 0 0 0 0 1 1/ 0 0 0 1

Inverse Perspective Projection: o If there is an Image point given by (xo, yo, 0), where Z=0 indicates the fact that Image plane is located at z=0. o This point can be represented in homogeneous form as: Ch= kxo kyo 0 k o Now we can apply Inverse Perspective Transform on C h.

Inverse Perspective Projection: Wh = = P-1 Ch

Inverse Perspective Projection: Wh W = = =

Inverse Perspective Projection: o This is obviously not, what one would expect, since it gives Z=0 for any 3 D point. o The problem here is caused by the fact that mapping a 3 D scene onto the Image Plane is a many-to-one transformation. o The image point (xo, yo) corresponds to a set of collinear points that lie on the line that passes through (xo, yo, 0) and (0, 0, ).

Inverse Perspective Projection: o The equations of this line in the world coordinate system are obtained as: o X=xo/ ( -Z) o Y=yo/ ( -Z) o These equations show that: “Unless we know something about the 3 D point that generated a given Image point (for example, its Z coordinate), we cannot completely recover the 3 D point from its Image. ”

Inverse Perspective Projection: o The above observation, can be used to formulate the Inverse Perspective transformation by using the Z component of Ch as a free variable, instead of 0. o Thus, let Ch= kxo kyo kz k

Inverse Perspective Projection: Wh = P-1 Ch

Inverse Perspective Projection: Wh = X W = Y Z =

Inverse Perspective Projection: o In simple words, treating Z as a free variable yields the following equations: n X= n Y= n Z=

Inverse Perspective Projection: o o Finally, for solving z in terms of Z in last equation, and substituting values in the first two expressions , yield: X = xo( -Z)/ Y = yo( -Z)/ This agrees with the observation that recovering a 3 D point from its Image by means of Inverse Perspective transformation requires knowledge of at least One of the world coordinate of the point.