PERSAMAAN NON LINEAR METODE TERBUKA Metode Newton Raphson

PERSAMAAN NON LINEAR METODE TERBUKA: • Metode Newton Raphson • Metode Secant

Metode Newton Raphson • adalah metode iterasi lain untuk memecahkan persamaan f(x)=0, dengan f diasumsikan mempunyai turunan kontinu f’

Metode Newton Raphson • menggunakan suatu nilai xi sebagai tebakan awal yang diperoleh dengan melokalisasi akar-akar dari f(x) terlebih dahulu • kemudian ditentukan xi+1 sebagai titik potong antara sumbu x dan garis singgung pada kurva f di titik (xi , f(xi)) • Prosedur yang sama diulang, menggunakan nilai terbaru sebagai nilai coba untuk iterasi seterusnya • Titik pendekatan ke n+1 dituliskan dengan: Xn+1 = xn -

Algoritma Metode Newton Raphson 1. Definisikan fungsi f(x) dan f’(x) 2. Tentukan toleransi error ( ) dan iterasi maksimum (n) 3. Tentukan nilai pendekatan awal x 0 4. Hitung f(x 0) dan f’(x 0) 5. Untuk iterasi i = 0 s/d n atau |f(xi)|> – Hitung xi+1 , f(xi+1) dan f’(xi+1) 6. Iterasi berhenti jika panjang selang baru (| xi+1 - xi|) < 7. Akar persamaan adalah nilai xi yang terakhir diperoleh

Contoh • Carilah akar positif dari fungsi f(x) = x 2– 5, dengan nilai tebakan awal x=1 • JAWAB −n = 7 – f(x) = x 2– 5 – f’(x) = 2 x – x 0 = 1 – f(1) = -4 – f’(1) = 2 − e = 0. 0000001 − x 1 = 1 – (-4/2) 3 − f(x 1) = f(3) = 32 – 5 4 − f’(x 1) = f’(3) = 2*3 6

Contoh • JAWAB – x 2 = 3 – (4/6) 2, 333333 – f(x 2) = f(2, 333333) = 2*3333332 – 5 0, 444444 – f’(x 2) = f’(2, 333333) = 2*2, 333333 4. 666667 – dst

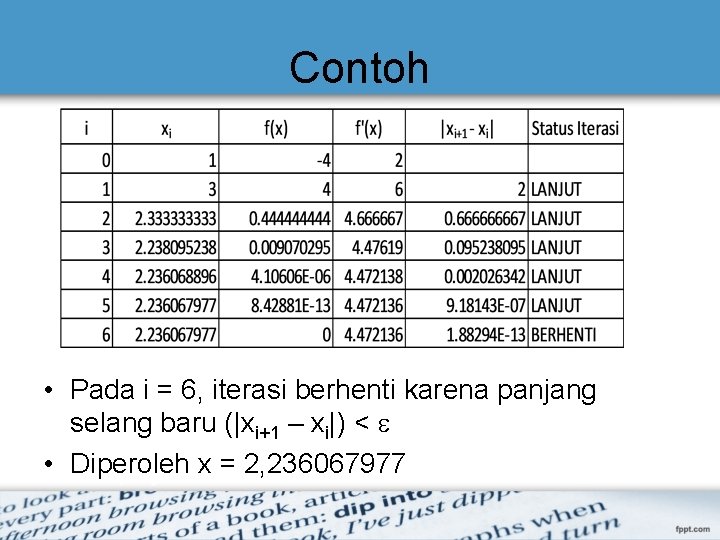
Contoh • Pada i = 6, iterasi berhenti karena panjang selang baru (|xi+1 – xi|) < • Diperoleh x = 2, 236067977

Permasalahan pada pemakaian metode newton raphson • Masalah potensial dalam implementasi metode Newton Raphson adalah evaluasi pada turunan • Tidak semua fungsi mudah dicari turunannya terutama fungsi yang bentuknya rumit.

Metode Secant • Turunan fungsi dapat dihilangkan dengan cara menggantinya dengan bentuk lain yang ekivalen • Modifikasi metode Newton Raphson dinamakan Metode Secant

Algoritma Metode Secant : • • • – • • sebaiknya gunakan metode tabel atau grafis untuk menjamin titik pendakatannya adalah titik pendekatan yang konvergensinya pada akar persamaan yang diharapkan Hitung f(xi-1) f(x 0) dan f(xi) f (x 1) Untuk iterasi i = 1 s/d n – • • Definisikan fungsi f(x) Definisikan torelansi error ( ) dan iterasi maksimum (n) Masukkan dua nilai pendekatan awal yang di antaranya terdapat akar yaitu xi-1 (x 0) dan xi (x 1) Hitung xi+1 dan f(xi+1) Iterasi berhenti jika panjang selang baru (| xi+1 - xi|) < Akar persamaan adalah nilai xi yang terakhir diperoleh

Contoh • Carilah akar dari fungsi f(x) = 2 x^3 - x -1, dengan nilai awal xi = 4, dan xi-1 = 2 dan = 0. 0000001

Contoh - Penyelesaian • f(x) = 2 x 3 - x -1, dengan nilai awal xi = 4, dan xi-1 = 2 dan = 0. 0000001 • xi-1 = 2 x 0 = 2 – f(xi-1) = f(x 0) = 2*23 -2 -1 13 • xi = 4 x 1 = 4 – f(xi) = f(x 1) = 2*43 -4 -1 123

Contoh - Penyelesaian • xi-1 = 2 x 0 = 2 – f(xi-1) = f(x 0) = 2*23 -2 -1 13 • xi = 4 x 1 = 4 – f(xi) = f(x 1) = 2*43 -4 -1 123 • x 2 = x 1 – (f(x 1)(x 1 – x 0))/(f(x 1) – f(x 0)) = 4 – (123*(4 -2))/(123 -13) 1, 7636363 – f(xi+1) = f(x 2) = 2* 1, 76363633 -1, 7636363 -1 8, 207639 • dst

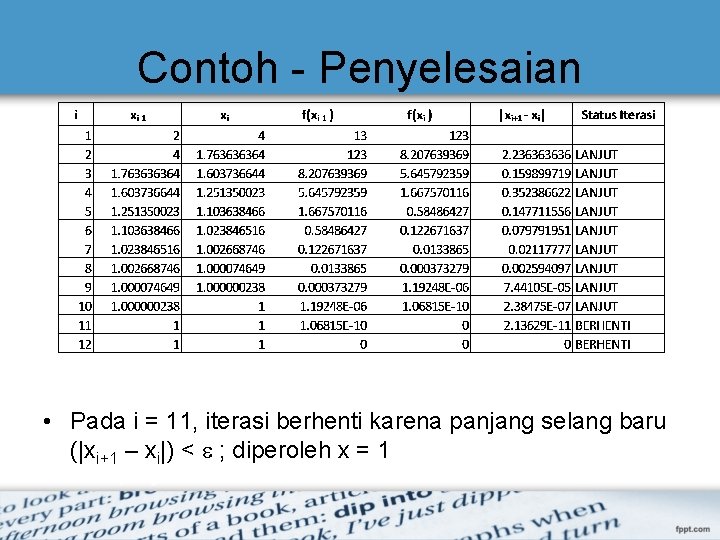
Contoh - Penyelesaian • Pada i = 11, iterasi berhenti karena panjang selang baru (|xi+1 – xi|) < ; diperoleh x = 1

TUGAS • Carilah akar persamaan f(x) = x 2 – 2 x – 3 dengan = 0, 000001 dengan metode Newton Raphson dan Secant! • Jawaban ditulis dengan pengolah kata dengan format nama file UW-METNUMT 02. doc • Kirim jawaban ke dianpraja@gmail. com dengan subject: [UW-METNUM-T 02. doc]