Persamaan Linier PL Penyelesaian PL dg eleminasi Penyelesaian

Persamaan Linier (PL) • Penyelesaian PL dg eleminasi • Penyelesaian PL dg subtitusi • Penyelesaian PL dg matriks • Penyelesaian PL dg gafis • Penyelesaian PL dg metode simplex Contoh: Carilah Penyelesaian a. persamaan 3 x + 4 y = 2 2 x – 3 y = 7 b. persamaan 3 x + 2 y = 19 4 x + 3 y = 26

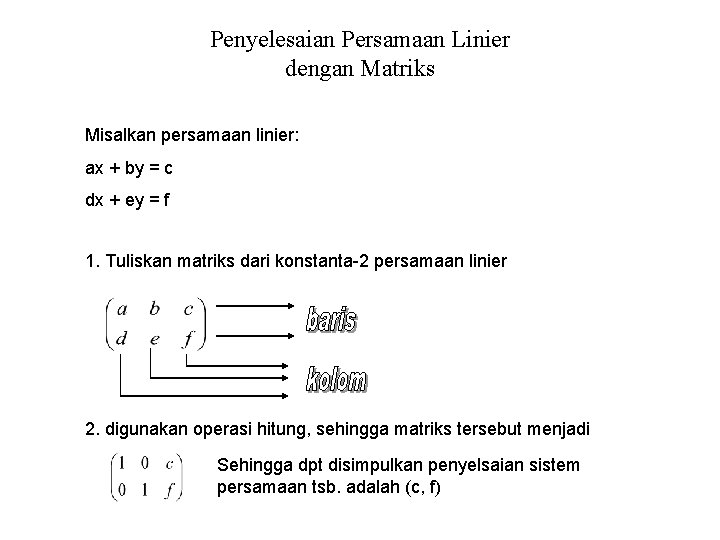
Penyelesaian Persamaan Linier dengan Matriks Misalkan persamaan linier: ax + by = c dx + ey = f 1. Tuliskan matriks dari konstanta-2 persamaan linier 2. digunakan operasi hitung, sehingga matriks tersebut menjadi Sehingga dpt disimpulkan penyelsaian sistem persamaan tsb. adalah (c, f)

Contoh: dik: sistem persamaan linier 3 x + 4 y = 2 2 x – 3 y = 7 1. Matriks dari konstanta-konstanta 2. Kalikan baris pertama dg 1/3 3. Kalikan baris pertama dg -2 kemudian tambahkan kpd baris kedua

4. Kalikan baris kedua dg -3/17 5. Kalikan baris kedua dg -4/3 kemudian tambahkan kpd baris pertama 6. Jadi penyelesaian sistem 3 x + 4 y = 2 2 x – 3 y = 7 Adalah (2, -1)

Latihan Carilah penyelesaian sistem: 3 x + 2 y = 19 4 x + 3 y = 26 Dengan bantuan matriks

Sistem Persamaan Linier dg 3 variabel Perhatikan: a 1 x + b 1 y + c 1 z = p a 2 x + b 2 y + c 2 z = q a 3 x + b 3 y + c 3 z = r Maka dari sistem persamaan linier 3 varibel di atas perlu diusahakan memperoleh matriks: Ini berarti penyelesaian sistem persamaan di atas (p, q, r)

Contoh: x - 4 z 2 x - y + 4 z 6 x – y + 2 z =5 = -3 = 10 Matriks dari konstanta-konstanta adalah: 1. Kalikan baris pertama dg -2 kemudian tambahkan kpd baris kedua

2. Kalikan baris pertama dengan -6, kemudian tambahkan kpd baris ketiga 3. Kalikan baris kedua dengan -1 4. Tambahkan baris kedua kpd baris ketiga, sehingga menjadi

5. Kalikan baris ketiga dengan 1/14 6. Kalikan baris ketiga dg 12 kemudian tambahkan hasilnya kpd baris kedua 7. Kalikan baris ketiga dg 4 kemudian tambahkan hasilnya kpd baris pertama didapat x = 3, y = 7, dan z = -1/2. jadi penyelesaiannya (3, 7, -1/2)

Latihan Selesaikan persamaan linier berikut dengan bantuan matriks: 2 x – y + z = -1 x – 2 y + 3 z = 4 4 x + y + 2 z = 4

Penyelesaian Sistem Persamaan Linier dengan Hukum Cramer 1. Determinan dari matriks: adalah: didefinisikan… = (ad – bc) 2. determinan dari adalah:

Perhatikan sistem persamaan linier a 1 x + b 1 y = c 1 a 2 x + b 2 y = c 2 apabila persamaan pertama kita kalikan dengan b 2, dan persamaan kedua dikalikan dengan –b 1, kemudian kita jumlahkan kedua persamaan itu, maka diperoleh (a 1 b 2 - a 2 b 1)x = c 1 b 2 – c 2 b 1, atau…… Analog, kita peroleh:

kalau maka dan Sistem persamaan tiga varibel a 1 x + b 1 y + c 1 z = d 1 a 2 x + b 2 y + c 2 z = d 2 a 3 x + b 3 y + c 3 z = d 3 dan determinan dari ; D≠ 0

Latihan: Selesaikan dengan menggunakan cara cramer persamaan linier berikut: 1. 2 x + 5 y = 7 5 x – 2 y = -3 2. x – 3 y + 7 z = 13 x+y+z =1 x – 2 y + 3 z = 4

Himpunan Penyelesaian Sistem Pertidaksamaan Linier Diketahui Pertidaksamaan Linier 2 x + y ≥ 2 4 x + 3 y ≤ 12 1/2 ≤ x ≤ 2 y≥ 0 Diktanyakan: 1. Gambar tiap persamaan tsb 2. Arsir daerah tiap pertidaksamaan 3. Gambar dalam satu bidang xoy kemudian arsir daerah yg memenuhi semua syarat di atas.

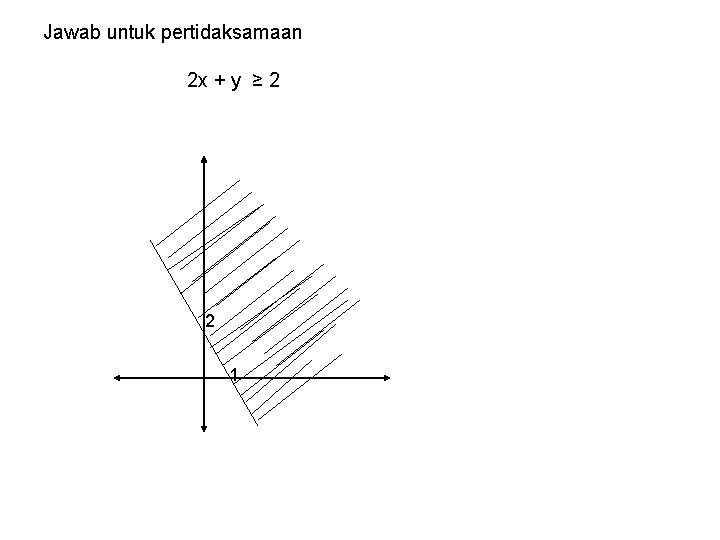
Jawab untuk pertidaksamaan 2 x + y ≥ 2 2 1

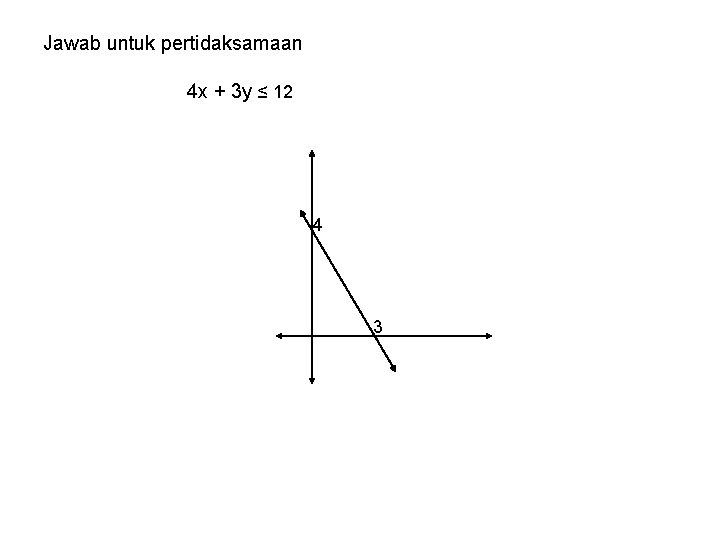
Jawab untuk pertidaksamaan 4 x + 3 y ≤ 12 4 3

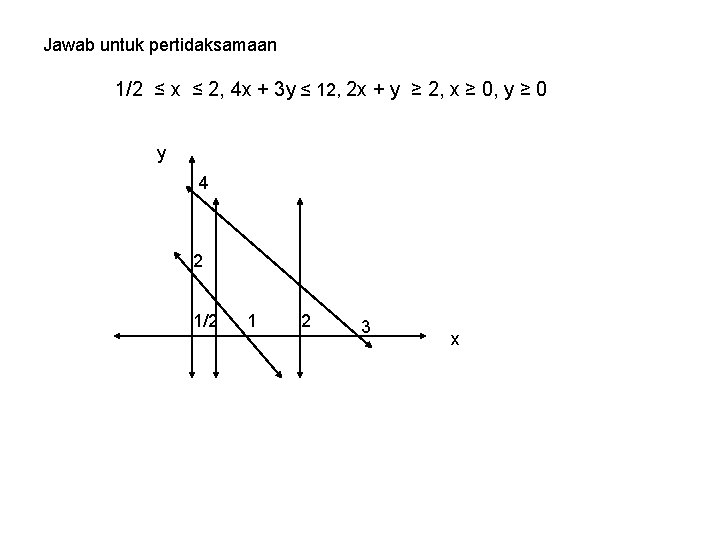
Jawab untuk pertidaksamaan 1/2 ≤ x ≤ 2, 4 x + 3 y ≤ 12, 2 x + y ≥ 2, x ≥ 0, y ≥ 0 y 4 2 1/2 1 2 3 x

Nilai Ekstrem Fungsi Linier Misalkan sistem pertidaksamaan linier sbb: 5 x + 6 y ≤ 30 , x≥ 0 3 x + 2 y ≤ 12 , y≥ 0 dan relasi T = x + 5 y, Carilah sepasang nilai (x, y) yang merupakan anggota penyelesaian pertidaksamaan di atas dan membuat nilai T optimum. 6 5 (3/2, 15/4) 4 6 x y T= x + 5 y 0 5 25 4 0 0 0 3/2 15/4 20, 25

Diketahui sistem pertidaksamaan: x–y+1≤ 0 x–y+3≥ 0 2≤x≤ 5 Carilah nilai maksimum dan minimum dari T = 9 x + 40 y jika (x, y) merupakan anggota himpunan penyelesaian sistem pertidaksamaan linier di atas.

Uraian dan Contoh: Peternak ayam potong memiliki sejumlah ayam yg tiap waktu tertentu dijual kepada konsumen berdasarkan berat badannya. Karena itu peternak tersebut berusaha memberi makanan yang memenuhi syarat agar ayam-ayam menjadi lebih berat dan harga per ekornya menjadi lebih mahal. Berdasarkan saran petugas kesehatan hewan, peternak perlu menggunakan bahan A dan bahan B yang harus dicampur sendiri supaya lebih ekonomis. Kedua bahan makanan tersebut mengandung sejumlah tertentu protein, mineral, vitamin, dan kalori. Bagaimana kombinasi kedua bahan itu agar biaya yang ditanggung serendah mungkin dan hasil yang diperoleh akan memenuhi syarat. Misal: bahan A adalah x bahan B adalah y, dan harga perunit bahan A adalah p Model Matematika: harga perunit bahan B adalah q Total biaya yang perlu dikeluarkan oleh peternak T = px + qy

T = px + qy adalah fungsi tujuan (objektif) 1. bahan A dan B bersifat non negatif variabel atau x ≥ 0 ; y ≥ 0 2. zat-zat yg terdapat bahan A dan B harus terpenuhi misalkan: jumlah minimum protein adalah c 1 jumlah minimum mineral adalah c 2 jumlah minimum vitamin adalah c 3 jumlah minimum kalori adalah c 3 dalam satu unit bahan A terpenuhi dalam satu unit bahan B terpenuhi protein sebanyak a 1 ; protein sebanyak b 1 mineral sebanyak a 2 ; mineral sebanyak b 2 vitamin sebanyak a 3 ; vitamin sebanyak b 3 kalori sebanyak a 4 ; kalori sebanyak b 4

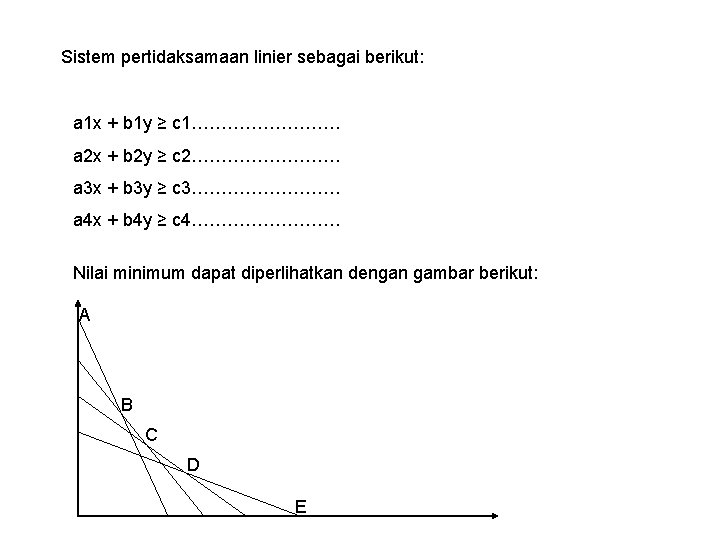
Sistem pertidaksamaan linier sebagai berikut: a 1 x + b 1 y ≥ c 1…………. a 2 x + b 2 y ≥ c 2…………. a 3 x + b 3 y ≥ c 3…………. a 4 x + b 4 y ≥ c 4…………. Nilai minimum dapat diperlihatkan dengan gambar berikut: A B C D E

LATIHAN 1. Seorang penjahit mempunyai bahan 60 m wol dan 40 m katun. Dari bahan tersebut akan membuat setelan jas dan rok untuk dijual. Satu setel jas memerlukan 3 m wol dan 1 meter katun; satu rok memerlukan 2 m wol dan 2 m katun. Berapa stel jas dan rok yg harus ia buat agar mendapat keuntungan sebesar-besarnya, bila satu stel jas harganya Rp 80. 000, 00 dan satu stel rok harganya Rp 40. 000, 00. 2. Terjemahkan dalam model matematika: 3. a. aktivitas (variabel) 4. b. fungsi tujuan 5. c. fungsi pembatas (constraints)

Jawab a. x adalah jumlah stelan jas b. y adalah jumlah stelan rok c. b. fungsi tujuan f(x, y) = 80. 000 x + 40. 000 y d. c. fungsi pembatas adalah: 3 x + 2 y ≤ 60; x + 2 y ≤ 40; x ≥ 0; y ≥ 0 e. d. Agar mencapai keuntungan sebesar-besarnya stel jas dan rok yg harus dibuat adalah: 30 20 20 40 x y f(x, y)=80000 x + 40000 y 0 20 800. 000 20 0 1. 600. 000 10 15 1. 250. 000

Latihan 1. Seorang petani memerlukan zat kimia A, B, C berturut 20 kg, 18 kg dan 12 kg, untuk memupuk kebun sayurnya. Dlm stiap kaleng pupuk cair mengandung zat A = 1 kg, ; B = 2 kg dan C = 3 kg. Pupuk kering tiap kantong mengandung zat A = 5 kg; B = 3 kg dan C = 1 kg. Harga 1 kaleng pupuk cair Rp 1000, - dan 1 kantong pupuk kering Rp 1. 500, -. Berapa banyak tiap jenis pupuk harus dibeli dg harga paling murah dengan zat yg diperlukan terpenuhi?

2. Seorang agen sepeda ingin membeli sepeda 25 buah untuk persediaan, ia ingin membeli sepeda biasa (jenis I) dg harga 60. 000/buah, dan sepeda balap (jenis II) dg harga 80. 000/buah. Ia merencanakan tidak akan mengeluarkan uang lebih dari Rp. 1. 680. 000, - dg harapan untung Rp 10. 000 utk sepda biasa dan Rp 12. 000 utk sepeda balap. Ditanyakan: a. aktivitas (variabel) b. fungsi tujuan (objektif) c. fungsi pembatas (constraints) 3. Suatu perusahaan bangunan merencanakan membangun rumah-2 untuk 540 org. Banyak rumah yg akan dibangun tidak lebih dari 120 buah. Rumah jenis I dg biaya sewa Rp 90. 000/tahun dan ditempati oleh 4 org; rumah jenis II dg sewa tiap tahun Rp 107. 000 dan dapat ditempati 6 orang. Ditanyakan: a. aktivitas b. fungsi tujuan c. fungsi pembatas

Penyelesaian Program Linier dengan cara Grafis a. Persoalan dengan jawaban tunggal contoh: sebuah pabrik baja mempunyai persdiaan 18 ton bahan mentah yg akan diproseskan menjadi besi beton dengan kontrak pembuatan 7, 6 ton dari bahan yg tersedia dan menjual sebagian bahan mentah kepada pabrik lain. Tercatat selama proses pembuatan besi beon berlangsung, 5% baja hilang. Berapa banyak bahan mentah yg dijual kepada pabrik lain? Jawab: 1. misal baja yg akan dijual adalah x ton 2. jumlah baja yg diproses menjadi besi beton (18 – x) ton 3. bahan mentah yg hilang selama proses menjadi besi beton (18 – x) – 5% (18 – x) = 95% (18 – x) = 7, 6. dengan demikian diperoleh : 18 – x = (7, 6) : (0, 95) = 10 ton jadi jumlah besi beton yg dpt dijual kepada pabrik lain adalah 10 ton.

Penyelesian sistem persamaan linier (PL) tiga variabel dengan cara grafis Tahapan proses penyelesaian dg 3 variabel: 1. Terjemahkan data persoalan PL menjadi sistem pertidaksamaan sebagai pembatas dan fungsi linier T = ax 1 + bx 2 + cx 3 sbg fungsi tujuan. 2. Lukis bidang datar dari tiap pembatas dan arsir ruang himpunan penyelesaian sistem pertidaksamaan linier 3. Menentukan titik dalam ruang penyelesaian yg memungkinkan fungsi tujuan mencapai nilai optimum

Persoalan tiga variabel: Fungsi tujuan: T =c 1 x 1 + c 2 x 2 + c 3 x 3 x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0 yang mencapai optimum Pembatasan: a 11 x 1 + a 12 x 2 + a 13 x 3 ≤ h 1 atau ≥ h 1 a 21 x 1 + a 22 x 2 + a 23 x 3 ≤ h 2 atau ≥ h 2 a 31 x 1 + a 32 x 2 + a 33 x 3 ≤ h 3 atau ≥ h 3

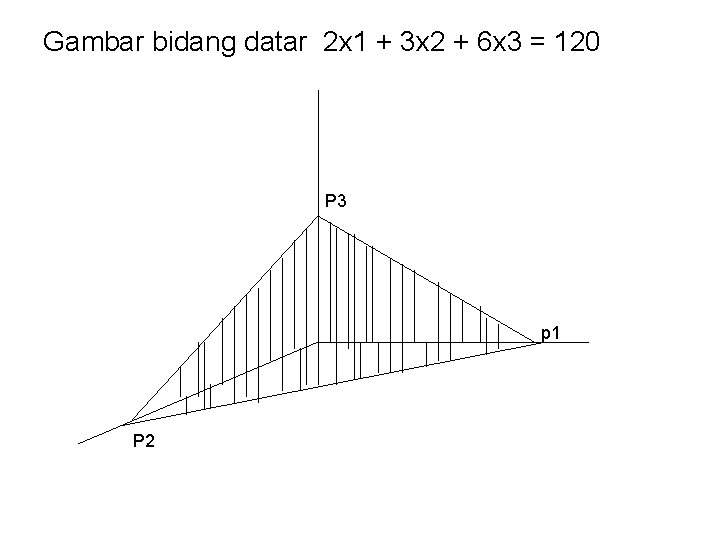
Contoh: Gambar bidang datar yang ditunjuk oleh: 2 x 1 + 3 x 2 + 6 x 3 = 120 Maka titik potong sumbu koordinat adalah: Pd. Sb x 1, bila x 2 = 0, x 3 = 0 mk P 1(60, 0, 0) Pd. Sb x 2, bila x 1 = 0, x 3 = 0 mk P 2(0, 40, 0) Pd. Sb x 3, bila x 1 = 0, x 2 = 0 mk P 3(0, 0, 20) Gambarlah bidang datar 2 x 1 + 3 x 2 + 6 x 3 = 120

Gambar bidang datar 2 x 1 + 3 x 2 + 6 x 3 = 120 P 3 p 1 P 2

Latihan 1: Gambar dalam satu sistem koordinat, ketiga bidang datar yg ditunjukkan oleh sistem persamaan linier berikut: 2 x 1 + 3 x 2 + 6 x 3 = 120 6 x 1 + 2 x 2 + 3 x 3 = 120 3 x 1 + 6 x 2 + 2 x 3 = 120

Latihan 2: Suatu perusahaan mempunyai 3 bahan mentah yaitu jenis I 480 unit, jenis II sebanyak 960 dan jenis III sebanyak 600 unit. Dari bahan mentah yg tersedia akan diproduksi tiga macam barang dg perincian, satu unit barang produksi memerlukan bahan mentah sbb: 1 unit brg A memerlukan 4 unit bahan I, 6 unit bahan II dan 6 unit bahan III. 1 unit brg B memerlukan 3 unit bahan I, 12 unit bahan II dan 5 unit bahan III 1 unit brg C memerlukan 6 unit bahan I, 8 unit bahan II dan 6 unit bahan III Harga penjualan brg A, 1 unit menghasilkan Rp 90. 000, Harga penjualan brg B, 1 unit menghasilkan Rp 60. 000, Harga penjualan brg C, 1 unit menghasilkan Rp 120. 000, Ditanyakan: Nilai maksimum fungsi tujuan…

Sistem Persamaan Linier lanjutan (persiapan simplex) Perhatikan sistem persamaan: 2 x 1 + 3 x 2 + 4 x 3 = 12 X 1 + 2 x 2 + 2 x 3 = 4 Jumlah baris m = 2 dan jumlah n = 3, atau jumlah variabel lebih dari jumlah persamaan, jika x 3=0 maka x 1 dan x 2 dpt dicari: 2 x 1 + 3 x 2 = 12 x 1 + 2 x 2 = 4

X 1 = 12; x 2 = -4; x 3 = 0 Adalah invers dari Jika x 1 = 0, maka x 2 dan x 3 dapat dicari 3 x 2 + 4 x 3 = 12 2 x 2 + 2 x 3 = 4 Sehingga diperoleh x 1 = 0; x 2 = -4; x 3 = 6 Bagaimana bila x 2 = 0, berapa nilai x 1 dan x 3 ?

Contoh Carilah pemecahan dasar dari sistem persamaan: X 1 + 2 X 2 + X 3 = 4 2 X 1 + 5 X 2 + 5 X 3 = 5 Jawab: 1. Banyaknya pemecahan dasar 3 C 2 = 3 2. Pemecahan dasar itu adalah 3. a) x 3 = 0; X 1 = …, dan x 2 = …. x 1 = 2; dan x 2 = 1 b) x 2 = 0, x 1 = ? dan x 3 = ? c) x 1 = 0, x 2 = ? dan x 3 = ?

Penyelsaian sistem persamaan linier dengan cara: 1. penghapusan dari Gauss 2. metode Gauss - Jordan Contoh: carilah penyelesaian daari sistem persamaan: 2 x 1 + x 2 + 4 x 3 = 16 3 x 1 + 2 x 2 + x 3 = 10 x 1 + 3 x 2 + 3 x 3 = 16 Jawab: a) dengan penghapusan Gauss pers (1) diperoleh x 1 + ½ x 2 + 2 x 3 = 8 atau x 1= 8 – 1/2 x 2 – 2 x 3 ……………. . (1’) nilai x 1 disubtitusikan ke dalam (2) dan (3) shg x 1 hilang dari pers. (2) dan (3) dari (2) 3 x 1 + 2 x 2 + x 3 = 10 menjadi………

3(8 – 1/2 x 2 – 2 x 3) + 2 x 2 + x 3 = 10 1/2 x 2 – 5 x 3 = -14……………(2’) dari (3) x 1 + 3 x 2 + 3 x 3 = 16 menjadi (8 – 1/2 x 2 – 2 x 3) + 3 x 2 + 3 x 3 = 16 21/2 x 2 + x 3 = 8……………. . (3’) persamaan (2’) dikalikan dengan 2 sehingga menjadi x 2 - 10 x 3 = 28 atau x 2 = -28 + 10 x 3………(2’’) kemudian disubtitusikan kedalam (3’) sehingga menjadi 21/2(-28 + 10 x 3) + x 3 = 8 -70 + 25 x 3 + x 3 = 8 26 x 3 = 78 atau x 3 = 3………(3’’) x 3 = 3 disubtitusikan kedalam (2’’) dan (1’’) sehingga merupakan penyelesaian sistem persamaan tsb di atas

b) dengan metode Gaus – Jordan langkah pertama kita gunakan cara penghapusan Gauss atau perhatikan sistem persamaan: x 1 + 1/2 x 2 + 2 x 3 = 8 ………………(1’) 1/2 x 2 – 5 x 3 = -14…………………. . (2’) 21/2 x 3 + x 3 = 8…………. (3’) dari (2’) 1/2 x 2 – 5 x 3 = -14 kita cari x 2 kemudian disubtitusikan kedalam (1’) dan (3’) x 2 = -28 + 10 x 3 kedalm (1’) menjadi: x 1 + 7 x 3 = 22 ………(1”) x 2 – 10 x 3 = -28……. (2”) x 3 = 3 ………………. (3”) kemudian x 3 = 3 disubtitusikan kedalam (1”) dan (2”) maka diperoleh x 1 = 1 dan x 2 = 2 atau matriks segitiga dari penghapusan Gaus diubah menjadi

Soal-soal 1. 2. Diketahui sistem persamaan x 1 + 2 x 2 + 3 x 3 + 4 x 4 = 7 2 x 1 + x 2 + x 3 + 2 x 4 = 3 a. berapa banyak pemecahan dasar maksimum yang mungkin diperoleh ? b. cari tipa pemecahan dasar yang mungkin dari sistem persamaan itu? Diketahui: 3 x 1 + 2 x 2 + 4 x 3 = 7 2 x 1 + x 2 + x 3 = 4 x 1 + 3 x 2 + 5 x 3 = 2 carilah pemecahan sistem persamaan itu dengan cara a. penghapusan Gaus b. Gauss-Jordan c. Cramer d. cari invers matriks dan cari pemecahan pers. itu