Persamaan Differensial Biasa PDB Ordinary Differential Equation ODE

Persamaan Differensial Biasa (PDB) Ordinary Differential Equation (ODE) Metode Numerik Teknik Sipil

Definisi Persamaan Differensial Biasa • Sebuah persamaan differensial biasa adalah sebuah persamaan yang menyatakan hubungan antara sebuah fungsi dengan sebuah variabel independen tunggal dan turunan total dari fungsi ini terhadap variabel independen tersebut. • Variabel dependen (y) tergantung kepada masalah fisik yang dimodelkan. Variabel independen biasanya salah satu dari variabel waktu (t) atau ruang (x).

Orde Persamaan Differensial Biasa • Orde PDB adalah turunan orde tertinggi dalam persamaan differensial. • Bentuk umum PDB orde satu adalah di mana f(t, y) disebut fungsi turunan. Untuk penyederhanaan notasi, turunan biasanya dinyatakan dengan tanda petik tunggal sehingga PDB mempunyai bentuk umum dimana superscript (n), (n-1), dst. menyatakan turunan orde ke n, n -1, dst.

Persamaan Differensial Biasa Linear dan Non-linear • PDB linear adalah PDB yang semua turunannya muncul dalam bentuk linear dan tidak ada koefisien yang tergantung kepada variabel dependen. • Koefisien bisa merupakan fungsi dari variabel independen, yang mana PDB disebut PDB linear dengan koefisien berubah. (linear, koef. konstan, PDB orde-satu) (linear, koef. berubah, PDB orde-satu) (bentuk umum PDB linear) • Jika koefisien tergantung kepada variabel dependen, atau turunan muncul dalam bentuk nonlinear, PDB-nya adalah nonlinear. Contoh: (bentuk umum PDB non-linear)

Persamaan Differensial Homogen dan Non-homogen • Persamaan differensial homogen adalah persamaan differensial di mana tiap suku melibatkan variabel dependen atau satu dari turunannya. • Persamaan differensial non-homogen mengandung suku tambahan, yg disebut suku non-homogen, suku-suku sumber (source terms), atau fungsi penggerak (forcing function), yang tidak melibatkan variabel dependen. Contoh: (linear, orde-satu, PDB homogen) (linear, orde-satu, PDB nonhomogen)

Sistem PDB • Banyak masalah praktis melibatkan beberapa variable dependen, yang masing-masing adalah sebuah fungsi dari variabel independen yang sama dan satu atau lebih variabel dependen, yang masing-masing dibangun oleh persamaan differensial biasa. Sekumpulan PDB ini disebut sistem PDB. Contoh: adalah sebuah sistem dari dua PDB orde satu

Klasifikasi PDB • Jika kondisi tambahan ditentukan pada nilai yang sama dari variable independen dan solusi digerakkan maju dari titik awal, persamaan differensial disebut sebagai PDB nilai awal. • Jika kondisi tambahan ditentukan pada dua nilai yang berbeda dari variabel independen, titik-titik akhir atau batas-batas dari daerah yang diperhatikan, persamaan differensial disebut PDB nilai batas.

Ilustrasi PDB nilai awal dan PDB nilai batas PDB nilai awal. Daerah solusi terbuka. PDB nilai awal diselesaikan dengan marching numerical methods PDB nilai batas. Daerah solusi tertutup. PDB nilai batas diselesaikan dengan marching numerical methods atau equilibrium numerical methods
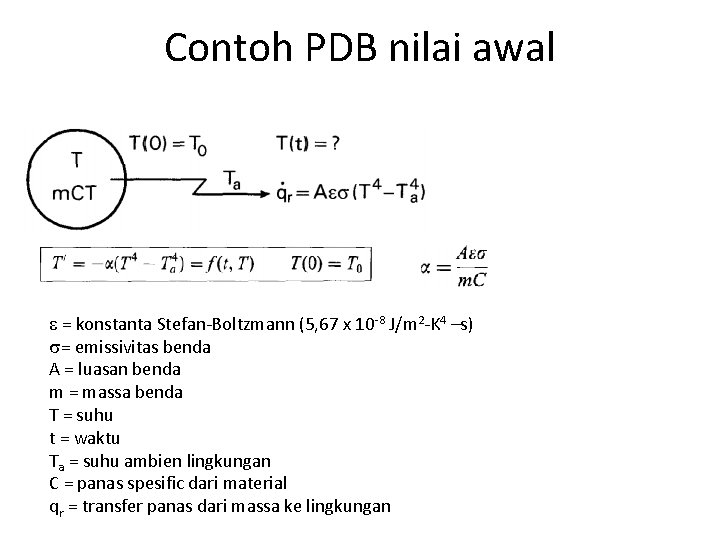
Contoh PDB nilai awal = konstanta Stefan-Boltzmann (5, 67 x 10 -8 J/m 2 -K 4 –s) s= emissivitas benda A = luasan benda m = massa benda T = suhu t = waktu Ta = suhu ambien lingkungan C = panas spesific dari material qr = transfer panas dari massa ke lingkungan
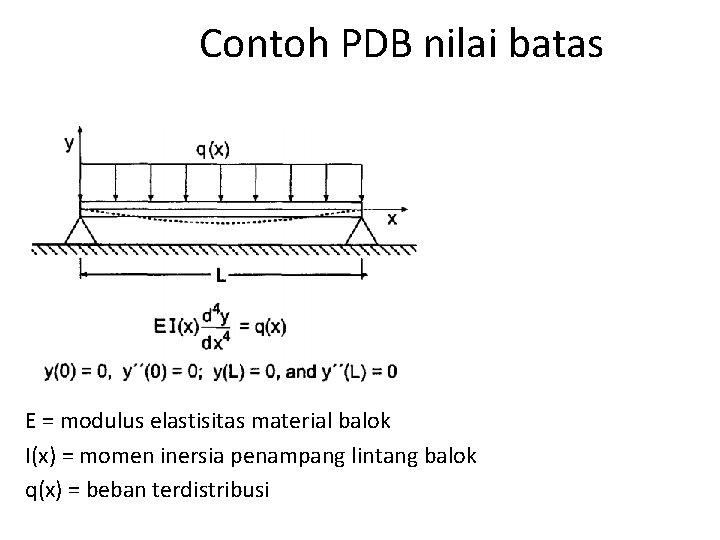
Contoh PDB nilai batas E = modulus elastisitas material balok I(x) = momen inersia penampang lintang balok q(x) = beban terdistribusi
- Slides: 10