PERMUTATIONS PERMUTATIONS EXERCISE 5 1 VERY SHORT ANSWER

PERMUTATIONS

PERMUTATIONS EXERCISE 5. 1 VERY SHORT ANSWER PROBLEMS

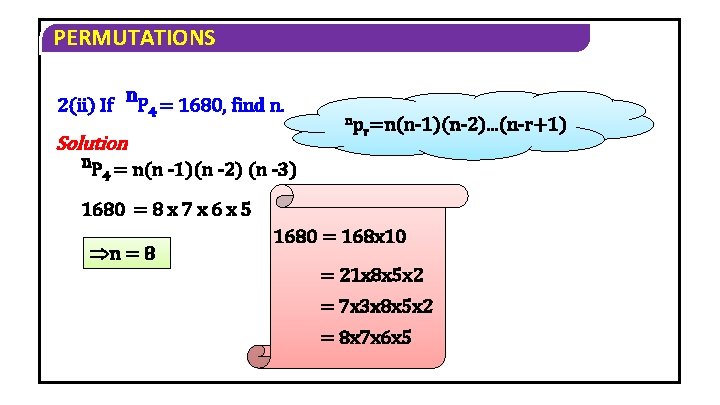
PERMUTATIONS 2(ii) If n. P 4 = 1680, find n. Solution np r=n(n 1)(n 2). . . (n r+1) n. P = n(n 1)(n 2) (n 3) 4 1680 = 8 x 7 x 6 x 5 n = 8 1680 = 168 x 10 = 21 x 8 x 5 x 2 = 7 x 3 x 8 x 5 x 2 = 8 x 7 x 6 x 5

PERMUTATIONS 2 (iii) If np 7 = 42. np 5 find n. Solution Given np 7 = 42. np 5 (n 5)(n 6)=42 n 2 11 n 12=0 (n 12)(n+1)=0 n=12 (∵ n is a positive integer)

PERMUTATIONS 3(i) If 12 Pr = 1320, find r. np Solution 12 p r =1320 12 p r= 12 p r=3 3 =12 x 11 x 10 =12 p 3 r=n(n 1)(n 2). . (n r+1)

PERMUTATIONS 4(i) If (n+1)P 5 : n. P 6 = 2 : 7 then find n. Solution 7(n+1)=2(n 4)(n 5)

PERMUTATIONS 7 n+7=2(n 2 9 n+20) 2 n 2 25 n+33=0 2 n 2 22 n 3 n+33=0 2 n(n 11) 3(n 11)=0 (n 11)(2 n 3)=0 n=11 (∵ n is integer) a positive

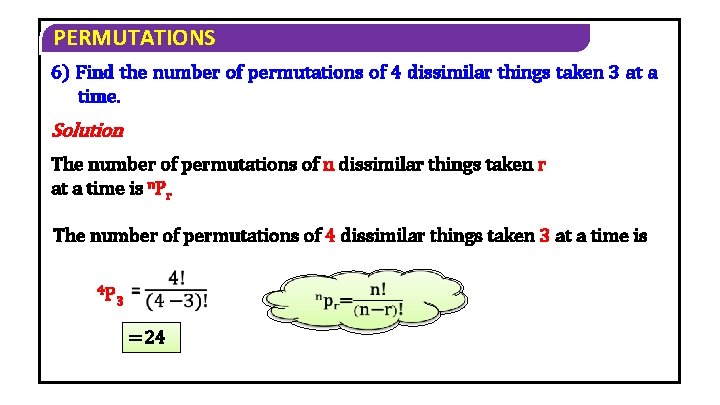
PERMUTATIONS 6) Find the number of permutations of 4 dissimilar things taken 3 at a time. Solution The number of permutations of n dissimilar things taken r at a time is n. Pr The number of permutations of 4 dissimilar things taken 3 at a time is 4 P 3 =24

PERMUTATIONS 8) If there are 25 railway stations on a railway line, how many single second class tickets must be printed so as to enable a passenger to travel from one station to another? TICKET IS Solution Given the number of stations on a railway --- To --line is 25. TO FILL 2 BLANKS WITH 25 STATIONS The number of single second class tickets must be printed so as to enable a passenger to travel from one station to another = The number of permutations of 25 things taken 2 at time = 25 p 2 = 25 x 24 =600

PERMUTATIONS 10) Find the number of ways of arranging the letters of the word ‘TRIANGLE’ so that the relative positions of the vowels and consonants are not disturbed. Solution In the given word ‘TRIANGLE’, the number of vowels are 3(I, A, E) and the consonants are 5 (T, R, N, G, L) C C V V C C C V The 3 vowels can be arranged in their relative positions in 3! ways and the 5 consonants can be arranged in their relative positions in 5! ways. By the counting principle, the required number of arrangements = 3! x 5! =720

PERMUTATIONS 12) Find the number of ways of arranging 5 boys and 4 girls in a row so that the row : (i) begins and ends with boys (ii) begins with a boy and ends with a girl. Solution (i) First and last places can be filled with 5 boys in 5 P 2 ways and the remaining 7 places can be filled with the remaining 7 persons in 7 P 7 = 7! ways. The required number of arrangements is B B 5 P 2 x 7! = 100800

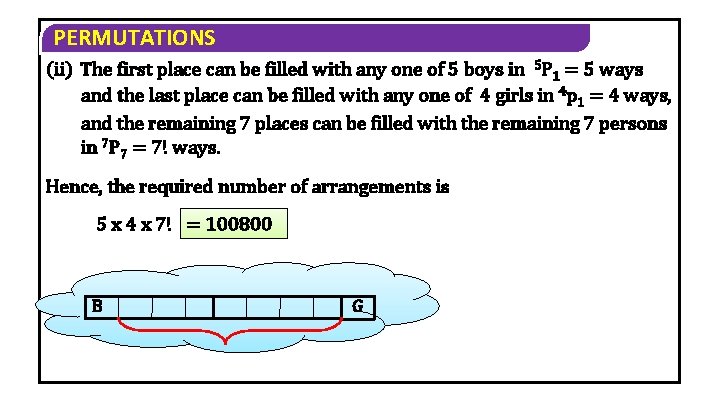
PERMUTATIONS (ii) The first place can be filled with any one of 5 boys in 5 P 1 = 5 ways and the last place can be filled with any one of 4 girls in 4 p 1 = 4 ways, and the remaining 7 places can be filled with the remaining 7 persons in 7 P 7 = 7! ways. Hence, the required number of arrangements is 5 x 4 x 7! = 100800 B G

PERMUTATIONS EXERCISE 5. 1 SHORT ANSWER PROBLEMS

PERMUTATIONS 2) Find the number of 4 letter words that can be formed using the letters of the word ‘MIRACLE’. How many of them …. (i) begin with a vowel (ii) begin and end with a vowel (iii) end with a consonant? Solution The word ‘MIRACLE’ has 7 letters. To get a 4 letter word, we have to fill 4 places with these 7 letters. Hence, the total number of 4 letter words that can be formed using these 7 letters is 7 p 4 = 840.

PERMUTATIONS (i) begin with a vowel In the word ‘MIRACLE’ there are 3 vowels (I, A, E) and 4 consonants (M, R, C, L). The first place can be filled by any one of 3 vowels in 3 p 1 = 3 ways. V The remaining 3 places can be filled by the remaining 6 letters in 6 P ways. 3 Hence the required number of arrangements is = 3 x 6 P 3 = 3 x 120 = 360

PERMUTATIONS (ii) begin and end with vowels The first and last places can be filled by 3 vowels in ways. V V 3 p 2 the remaining 2 places can be filled by the remaining 5 letters in 5 P 2 ways. Hence, the required number of arrangements = 3 P 2 5 P 2 = 6 20 = 120

PERMUTATIONS (iii) end with a consonant The last place can be filled by any one of the 4 consonants in 4 P 1 = 4 ways C The remaining 3 places can be filled with the remaining 6 letters in 6 P 3 ways. Hence, the required number of arrangements is =4 x 6 P 3 = 480

PERMUTATIONS 4) Find the number of ways of permuting the letters of the word ‘PICTURE’ so that i) all the vowels come together. ii) no two vowels come together. iii) the relative positions of vowels and consonants are not disturbed. Solution (i) all the vowels come together. 4 Given word PICTURE contains 3 vowels (I, U, E)and (P, C, T, R) consonants Since all the vowels are to be together, treat the 3 vowels as one unit.

PERMUTATIONS This unit and the remaining 4 consonants can be arranged in a row in 5! ways. Then how many things do we have? One unit+4 consonants =5 Now, the 3 vowels in the unit can be arranged among themselves in 3! ways. Hence the required number of arrangements is = 5! x 3! = 120 x 6 = 720

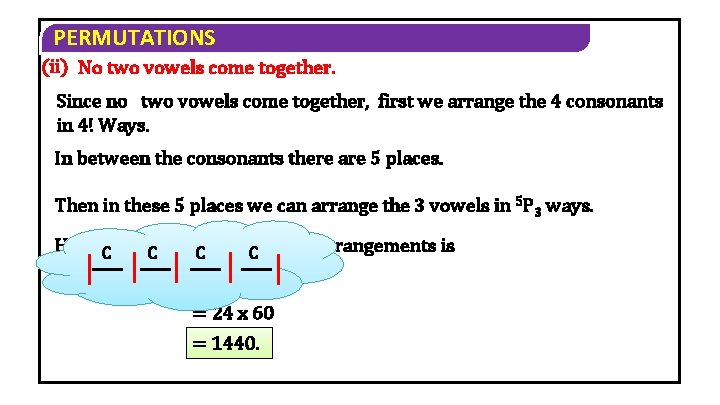
PERMUTATIONS (ii) No two vowels come together. Since no two vowels come together, first we arrange the 4 consonants in 4! Ways. In between the consonants there are 5 places. Then in these 5 places we can arrange the 3 vowels in 5 P 3 ways. Hence. Cthe required of arrangements is C C number C = 4! x 5 P 3 = 24 x 60 = 1440.

PERMUTATIONS (iii) The relative positions of vowels and consonants are not disturbed. In the given word ‘PICTURE’, the number of vowels are 3 (I, U, E) and the consonants are 4 (P, C, T, R) C V C V The 3 vowels can be arranged in their relative positions in 3! ways and the 4 consonants can be arranged in their relative positions in 4! ways. By the counting principle, the required number of arrangements = 3! x 4! =144

PERMUTATIONS 6) Find the number of ways of arranging 5 different mathematics books, 4 different physics books and 3 different chemistry books such that the books of the same subject are together. Solution Let us consider 5 Mathematics books as 1 st unit, 4 Physics books as 2 nd unit and 3 Chemistry books as 3 rd unit. These 3 units can be arranged in 3! ways. Now 5 mathematics books in the 1 st unit can themselves in 5! ways. be arranged among

PERMUTATIONS 4 Physics books in the 2 nd unit can be arranged among themselves in 4! ways. 3 Chemistry books in the 3 rd unit can be arranged among themselves in 3! ways Hence, the required number of arrangements is = 3! x 5! x 4! x 3! = 6 x 120 x 24 x 6 = 103680

PERMUTATIONS 8) Find the number of ways of seating 10 students A 1 , A 2 , ……. . , A 10 in a row such that : (i) A 1, A 2, A 3 sit together Solution Since A 1, A 2, A 3 sit together, consider them as 1 unit and remaining 7 as 7 different units. Total number of units = 1 + 7 = 8. These 8 units can be arranged in 8! ways.

PERMUTATIONS A 1, A 2, A 3 in the unit can be arranged among themselves in 3! ways. Hence, the required number of arrangements is 8! x 3!

PERMUTATIONS (ii) A 1, A 2, A 3 sit in a specified order. Solution Since they sit in a specified order Since A 1, A 2, A 3 sit in a specified order, first of all arrange the remaining 7 persons in ten places in 10 P 7 ways. In the remaining 3 places A 1, A 2, A 3 can be arranged in only one way. Hence , the required number of arrangements is 10 P 7 x 1

PERMUTATIONS (iii) A 1, A 2, A 3 sit together in a specified order. Solution Since A 1, A 2, A 3 sit together, consider them as 1 unit and the remaining 7 as 7 different units. Total number of units = 1 Since + 7 they = 8. sit in a specified order These 8 units can be arranged in 8! ways. A 1, A 2, A 3 among themselves they can be arranged in only one way. Hence, the required number of arrangements is 8! x 1= 8!

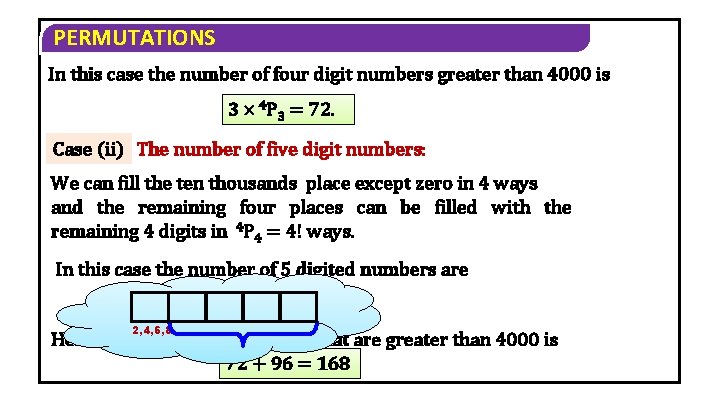
PERMUTATIONS 10) Find the number of numbers that are greater than 4000 which can be formed using the digits 0, 2, 4, 6, 8 without repetition. Solution All 4 digited numbers begin with 4 or 6 or 8 greater than 4000 and all 5 digited numbers greater than 4000 Case (i) 4, 6, 8 The number of 4 digited numbers greater than 4000 We can fill the thousand’s place with 4 or 6 or 8 in 3 ways and the remaining three places can be filled with the remaining four digits in 4 P 3 ways.

PERMUTATIONS In this case the number of four digit numbers greater than 4000 is 3 4 P 3 = 72. Case (ii) The number of five digit numbers: We can fill the ten thousands place except zero in 4 ways and the remaining four places can be filled with the remaining 4 digits in 4 P 4 = 4! ways. In this case the number of 5 digited numbers are 4 x 4! = 96. 2, 4, 6, 8 Hence the number of numbers that are greater than 4000 is 72 + 96 = 168

PERMUTATIONS 11) Find the number of 4 digited numbers that can be formed using the digits 2, 3, 5, 6, 8 (without repetition). How many of them are divisible by (i) 2 (ii) 3 (iii) 4 (iv) 5 (v) 25 Solution The number of 4 digit numbers that can be formed using given 5 digits without repetition is 5 P 4 = 120.

PERMUTATIONS (i) Divisible by 2: A number is divisible by 2, if the unit’s place contains even digit To get a number which is divisible by 2, we have to fill up the units place either with 2 or 6 or 8 in 3 ways. 2, 6, 8 Now, the remaining 3 places can be filled with the remaining 4 digits in 4 P = 24 ways. 3 Hence , the number of 4 digit numbers divisible by 2 is 3 x 24 = 72

PERMUTATIONS (ii) Divisible by 3: A number is divisible by 3, if the sum of the digits in that number is a multiple of 3. If we 3 or 56 digits from is 24. The sum ofremove the given digits, the sum is divisible by ‘ 3’. The four digits such that their sum is a multiple of 3 from the given digits are 2, 5, 6, 8 or 2, 3, 5, 8. In each case, they can be arranged in 4! ways. ∴ The total number of 4 digit numbers divisible by 3 4! + 4! = 2 4! = 48

PERMUTATIONS (iii) Divisible by 4: A number is divisible by 4, if the number formed by the digits in the last two places (unit’s and Ten’s places) is a multiple of 4. We fill the last two places with 28 (or) 32 (or) 36 (or) 52 (or) 56 (or) 68 in 6 ways. x x After filling the last two places, we can fill the remaining two places with the remaining 3 digits in 3 P 2 = 3! = 6 ways ∴ The total number of 4 digit numbers divisible by 4 is 6 6 = 36

PERMUTATIONS (iv) Divisible by 5: A number is divisible by 5, if the unit’s place contains either 0 or 5. From the given digits units place can be filled in one way, (i. e. with 5) 5 The remaining 3 places can be filled with the remaining 4 digits in 4 P 3 ways. ∴ The total number of 4 digit numbers divisible by 5 is 1 4 P 3 = 4! = 24

PERMUTATIONS (v) Divisible by 25: A number is divisible by 25, if the number formed by the digits in the last two places is 25 or 50 or 75 or 00 From the given digits the last 2 places can be filled by 25 in only one way. 2 5 The remaining 2 places can be filled with remaining 3 digits in 3 P 2 = 6 ways. ∴ The total number of 4 digit numbers divisible by 25 is 1 x 6 = 6.

PERMUTATIONS 12) Find the sum of all 4 digited numbers that can be formed using the digits 1, 3, 5, 7, 9. Solution The number of 4 digited numbers that can be formed using the digits 1, 3, 5, 7, 9 is 5 P 4 = 120. out of these 120 numbers

PERMUTATIONS 1 4 digited numbers contain 1 in unit’s place are 4 P 3 4 P 4 digited numbers contain 1 in ten’s place are 1 3 Since 3 empty places are filled with the 4 4 digited 1 remaining‘ 4’ digits numbers contain 1 in hundred’s place are P 3 1 4 digite numbers contain 1 in thousand’s place are 4 P 3

PERMUTATIONS The contribution of 1 to the sum = (4 P 3 x 1 x 1) +( 4 P 3 x 1 x 100 )+( 4 P 3 x 1 x 1000) =4 P 3 x 1 x(1+10+1000 ) =4 P 3 x 1 x(1111) Similarly, value contributed by 3 to the sum = 4 P 3 x (1111) value contributed by 5 to the sum = 4 P 3 x 5 x (1111) value contributed by 7 to the sum = 4 P 3 x 7 x (1111) value contributed by 9 to the sum = 4 P 3 x 9 x (1111)

PERMUTATIONS ∴ The sum of all 4 digited numbers =4 P 3 x 1 x(1111)+4 P 3 x 3 x(1111)+4 P 3 x 5 x(1111) + 4 P 3 x 7 x(1111) + 4 P 3 x 9 x (1111) = 4 P 3 x(1111) x (1+3+5+7+9) = 24 x(1111) x 25 = 600 x(1111) = 6, 600

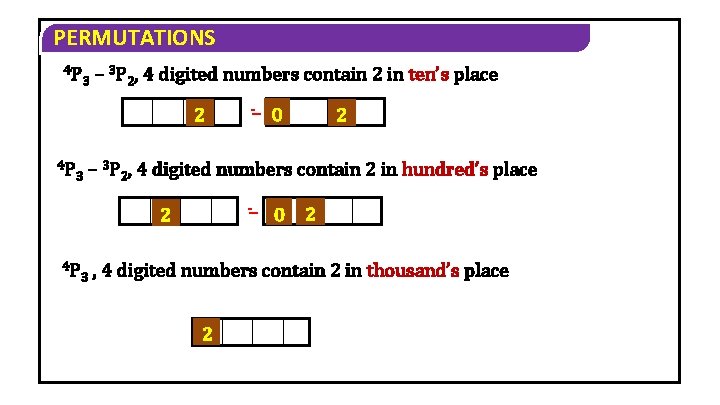
PERMUTATIONS 13) Find the sum of all 4 digited numbers that can be formed using the digits 0, 2, 4, 7, 8 without repetition. Solution The number of 4 digit numbers that can be formed by using the digits 0, 2, 4, 7, 8 is 5 P 4 4 P 3 – 4 P 3 = 96. Out of these 96 numbers – 3 P 2, 4 digited numbers contain 2 in units place 2 – 0 2

PERMUTATIONS 4 P 3 – 3 P 2, 4 digited numbers contain 2 in ten’s place 2 4 P 3 0 2 – 3 P 2, 4 digited numbers contain 2 in hundred’s place – 2 4 P – 3 0 2 , 4 digited numbers contain 2 in thousand’s place 2

PERMUTATIONS The contribution of 2 to the sum 4 3 = (4 P 3 3 P 2 ) x 2 x +(4 P 3 3 P 2 ) x 2 x 10+ ( P 3 P 2 ) x 2 x 100 +( 4 P 3 ) x 2 x 1000 1 = 4 P 3(2+20+2000) 3 P 2(2+20+200) = 4 P 3 x 2 x(1111) 3 P 2 x 2 x (111)

PERMUTATIONS Similarly, the value contributed by 4 to the sum = 4 P 3 x 4 x(1111) 3 P 2 x 4 x (111) the value contributed by 7 to the sum = 4 P 3 x 7 x(1111) 3 P 2 x 7 x (111) the value contributed by 8 to the sum = 4 P 3 x 8 x(1111) 3 P 2 x 8 x (111)

PERMUTATIONS ∴ sum of all 4 digit numbers ={ 4 P 3 x 2 x(1111) 3 P 2 x 2 x (111) }+{ 4 P 3 x 4 x(1111) 3 P 2 x 4 x (111)} +{ 4 P 3 x 7 x(1111) 3 P 2 x 7 x (111)} +{ 4 P 3 x 8 x(1111) 3 P 2 x 8 x (111)} =( 4 P 3) x(1111) x (2+4+7+8) 3 P 2 x(111) x (2+4+7+8) =24 x 21 x (1111) – 6 x 21 x (111) =5, 59, 944 – 13, 986 = 5, 45, 958

PERMUTATIONS Note v The sum of r digited numbers that can be formed using ‘n’ non zero distinct digits (1 ≤ n ≤ 9) and r ≤ n is (sum of n digits) (n 1)P(r 1) (111……. r times). v The sum of r digited numbers that can be formed using ‘n’ distinct digits (zero is included) 1 ≤ n ≤ 9 and r ≤ n is {(Sum of n digits) (n 1)P(r 1) (111…. . r times)} – {(Sum of n digits) (n 2)P(r 2) (111…. . (r 1) times)}

PERMUTATIONS 14) The letters of the word ‘PRISON’ are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the rank of the word ‘PRISON’. Solution The alphabetical order of the letters of the word ‘PRISON’ is I, N, O, P, R, S In dictionary order all the words that begin with I comes first, if I occupies the first place then the remaining 5 places can be filled with remaining 5 letters in 5! ways.

PERMUTATIONS The number of words which begin with I = 5! = 120. I 5! The number of words which begin with N = 5! = 120. N 5! The number of words which begin with O = 5! = 120. O 5!

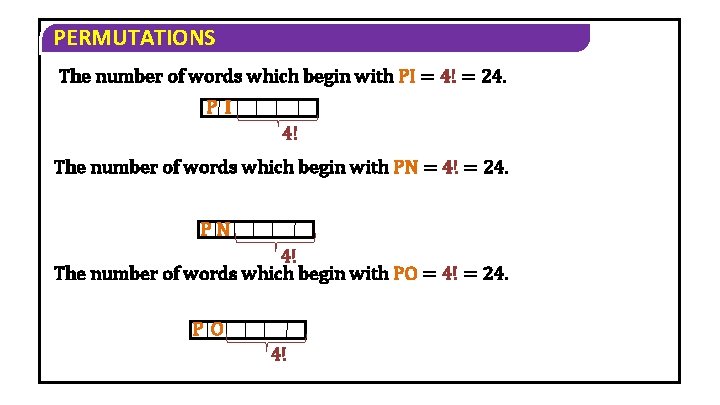
PERMUTATIONS The number of words which begin with PI = 4! = 24. PI 4! The number of words which begin with PN = 4! = 24. PN 4! The number of words which begin with PO = 4! = 24. PO 4!

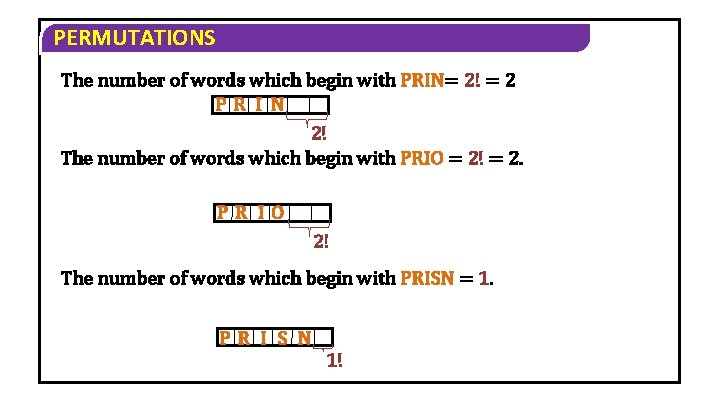
PERMUTATIONS The number of words which begin with PRIN= 2! = 2 PR I N 2! The number of words which begin with PRIO = 2! = 2. PR IO 2! The number of words which begin with PRISN = 1. PR I S N 1!

PERMUTATIONS The next word is PRISON Hence, the rank of the word ‘PRISON’ = 120 + 24 + 2 + 1 = 438

PERMUTATIONS Thank you…