Permutation Groups Definitions A Permutation of a set

Permutation Groups – Definitions A Permutation of a set A is a function from A to A which is both one to one and onto So in a Permutation on set A, the range and the domain of the function are both the set A. Recall from earlier work: A function from set A to set B is a rule which assigns to each element of A (the domain) exactly one element of B (the range) One to one means f(a)=f(b) implies that a=b. Onto means every element of B is the image of least one element of A under f. rubic cube permutation group http: //en. wikipedia. org/wiki/Permutation_group

Permutation Groups – Definitions: A Permutation Group of a set A is a set of Permutations on A which form a group under function composition. That is, the elements are functions from A to A which are both one to one and onto, and the binary operation is function composition, Recall from earlier work: A group has elements which include identity and inverses, and an operation which is associative and closed. So here, the elements are functions and the operation is function composition, which is always associative (although not usually commutative. ) This may take some “getting used to”, because in most of the groups we have seen so far, the elements are values and

Permutation Groups -- Discussion So in a Permutation Group, we need functions and their inverses; also we need an identity function. Recall from earlier work that a function has an inverse if and only if it is one to one and onto. Since functions are group elements, we expect that a function composed with its inverse will result in the identity function, as indeed it does. At this time we are mainly concerned with permutations on a finite set, so we can build closure into the function definitions.

Permutation Groups – Notations In other areas such as algebra and calculus, functions are defined on infinite sets and often written as algebraic formulas. However, in this context we usually define a function explicitly, by listing an element of the domain along side its corresponding function value. There are two ways this is commonly done: grid notation (due to Euler) and cycle notation (due to Cauchy). math cartoons from http: //www. math. kent. edu/~sather/ugcolloq. html

Permutation Groups – Notations Example, D 4, the symmetries of a Square Consider D 4, the symmetry group of a square. We can represent this group as a permutation group in grid notation as follows. Number the four corners of the square: 1, 2, 3, 4 as shown. Or, in cycle notation we can write: R 90 = (1 2 3 4) and Fh= (1 2)(3 4) 3 2 4 1 Then we can represent a 90 o counterclockwise rotation as: R 90 = 1 2 3 4 2341 and a reflection across the horizontal axis as: F h= 1 2 3 4 2143

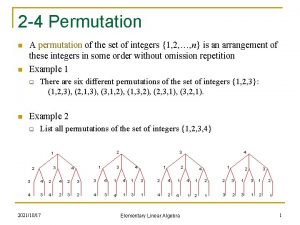
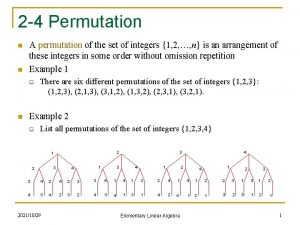
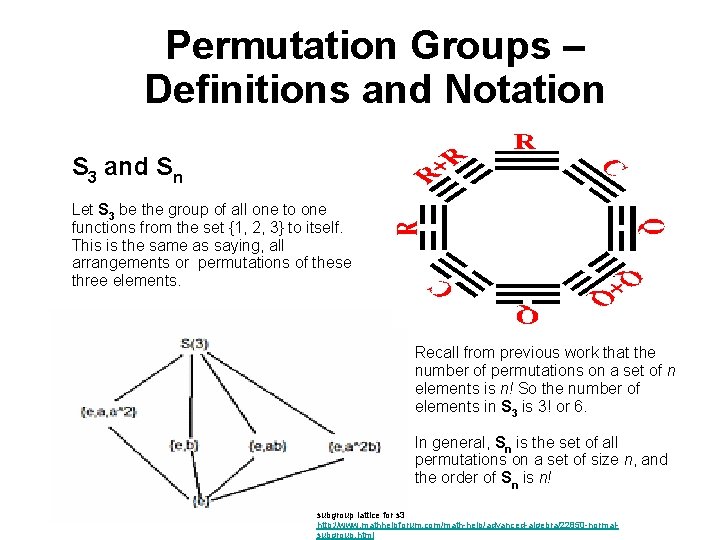
Permutation Groups – Definitions and Notation S 3 and Sn Let S 3 be the group of all one to one functions from the set {1, 2, 3} to itself. This is the same as saying, all arrangements or permutations of these three elements. Recall from previous work that the number of permutations on a set of n elements is n! So the number of elements in S 3 is 3! or 6. In general, Sn is the set of all permutations on a set of size n, and the order of Sn is n! subgroup lattice for s 3 http: //www. mathhelpforum. com/math-help/advanced-algebra/22850 -normalsubgroup. html

Cauchy Cycle Notation Disjoint Cycles Commute Order of a Permutation Cycle notation, introduced by Cauchy, has many advantages over grid notation. In general, the product of cycles does not commute. However, we can write any permutation as a cycle or a product of disjoint cycles, that is, each element of the set appears in at most one cycle. Written in this form, disjoint cycles commute. Also when we write a permutation in this form, the order of the permutation (that is, the smallest number of times we need to repeat that permutation to obtain the identity permutation) is the least common multiple of the lengths of the cycles.

Cycle Notation Decomposition into two-cycles Always even or always odd Identity is always even Any permutation may also be written or “decomposed” as a product of two-cycles. This product would usually not be disjoint, and it need not be unique. However, if a permutation can be written as an odd number of two-cycles, any other decomposition of that permutation is also an odd number of two cycles. Similarly, if a permutation can be written as an even number of two-cycles, any other decomposition of that permutation is also an even number of two cycles. The identity permutation is always an even number of two-cycles. “I’m odd and I’ll always be odd!-- Joni This oddfellow is still odd even though he’s decomposed! IOOF tombstone

Cycle Notation Definitions, Examples Even Permutation Odd Permutation If a permutation can be written as an odd number of two cycles, we say it is an odd permutation. Examples of decomposition into 2 cycles: If a permutation can be written as an even number of two cycles, we say it is an even permutation. Notice that (12345) is a cycle of length 5, and 5 is an odd number – yet (12345) can be written as an even number of two-cycles so it is an even permutation. “A cycle of odd length is always even – now that's odd! “ -- Rus (12345) = (15)(14)(13)(12) (1234) = (14)(13)(12) (1234)(247)=(14)(13)(12)(27)(24) However, (1234), a cycle of length 4 is an odd permutation because it can be written as an odd number of twocycles, even though 4 is an even number.

An The Alternating Groups of Degree n For any n, the set of even permutations in Sn forms a group, and a subgroup of Sn. This is because the inverse of an even permutation is always even, the composition of even cycles is always even, and the identity can always be written as an even cycle. This group is called An, the alternating group of degree n. When n ≠ 1, An is of order n!/2 Permutation group A 5 http: //www. math. metu. edu. tr/~berkman/466 object. html The Alternating groups are very important in historical, theoretical, and applications contexts. permutation group A 4 http: //faculty. smcm. edu/sgoldstine/origami/display text. html Note that the set of odd permutations do not form a group, because this set lacks the identity permutation and lacks closure under composition.

Suggested Activities Cycle Notation, more practice Cycle notation, introduced by Cauchy, has many advantages over Euler's grid notation, although some people may require more practice to perform calculations quickly and accurately in this notation. For practice, try verifying the Cauchy table for A 4 on page 105 of the text, by multiplying out each pair of elements and showing that the product is as stated in the table.

Suggested Activities Reinforcement of Knowledge Base Modern educational practices tend to de-emphasize knowledge base in favor of constructivist education theory, which is thought to better support higher order thinking. However, for most people*, an extensive knowledge base is necessary for mastery of this subject. Please see the textbook author Gallian’s comments this matter, on his website http: //www. d. umn. edu/~jgallian under the heading “Advice for students for One who has the facts memorized with understanding is comparable to learning abstract algebra” *Sylvester notwithstanding, text pg 89 Tools 3 www. istockphoto. com tools and rocks www. dkimages. com a highly skilled worker who has the proper tools on hand knows how to use them, rather than having to scrounge around and improvise with a stick or a rock!

Suggested Activities: Reinforcement of Knowledge Base according to individual learning style Often students complain that memorizing facts and definitions is excessively difficult, or that knowledge obtained this way does not seem to apply to testing or problem solving situations. Complaints like this often result from failure to adapt study habits to one's particular learning style. For example, a visual learner may get by with simply reading over text or notes, while an aural learner may need to say lessons out loud or even set them to music. A kinesthetic learner often needs to re-write the lessons, make models, demonstrate the information to others, etc. Although kinesthetic methods are more demanding in terms of time and energy, all learners benefit from kinesthetic learning methods, because these methods produce more robust memory traces in the brain.

Suggested Activities: Reinforcement of Knowledge Base according to individual learning style Please visit one or both of these sites to find out or confirm your learning style: http: //www. usd. edu/trio/tut/ts/stylestest. html for a brief quiz and classification into one of three styles, or http: //www. learning-styles-online. com for a more extensive questionnaire and classification into one of six styles. This site will generate a detailed description of your learning style and a graph showing your style according to six axes. Both sites have been checked for safety from malware, and contain recommendations and resources for the various learning styles. This is a sample Memletics Learning Styles graph produced by the online test at http: //www. learning-styles-online. com/inventory/ Picture credit http: //www. learning-styles-online. com/inventory/

Suggested Activities: Online Resources provided by Text Author J. A. Gallian http: //www. d. umn. edu/~jgallian Practice with the true-false questions and flashcards provided on this website may be particularly helpful for building and reinforcing knowledge base. The flashcards may be printed out or used in software form, from the website. This website also contains links to some useful software. In particular, the Group Explorer software, available on the above website by following the link Group Explorer, or one may go directly to: http: //groupexplorer. sourceforge. net/ quarternion group from http: //home. att. net/~numericana/ answer/groups. htm rock stack from loveringllc. com

Suggested Activities: Other Online Resources Here a few other good online resources. All of these have been checked for malware and are safe. http: //en. wikipedia. org/wiki/Group_theory (a good starting point) http: //www. math. miami. edu/~ec/book/ (a free online book on abstract algebra) http: //en. wikipedia. org/wiki/Dihedral_group (explains the dihedral groups) http: //members. tripod. com/~dogschool/cyclic. html I (explains Cauchy cycle notation) http: //en. wikipedia. org/wiki/Euler%27 s_totient_function (Totient function, in Gallian text referenced in connection with U-groups) http: //members. tripod. com/~dogschool/index. html (an index to another online text) http: //en. wikipedia. org/wiki/Symmetric_group (explanations and applications of symmetric groups) http: //www. t 209. com/article. php? art_id=26 (a vbasic program φ(n) for numbers up to 231) http: //eldar. mathstat. uoguelph. ca/dashlock/math 3130/pdf/Chapter 2 b. pdf (another explanation of Cayley cycle notation) http: //www. mathwire. com/seasonal/winter 07. html

Acknowledgments Dr. T. Englund, Professor of Mathematics, Central Washington University, professor for Mathematics 461 Dr. T. Willard, Professor of Mathematics, Central Washington University, graduate adviser I am grateful for the cooperation of the following fourth year undergraduate Mathematics students at Central Washington University, who included me in their study group for the final exam. Notes from this study group were then composed into this presentation: Amber Goodrich, Mike Prothman, Russel Hess, David Melik, Geoff La. Brandt, Brandon Belieu, Special thanks to: Two Bears, my brother St. Euler St. Cauchy All graphics in this presentation not created by J. Pinkney are reproduced from online sources according to the Fair Use Provisions of the U. S. Copyright Act, with the html sources cited in the frame on which they appear.