Periodic Signal Spectra Chapter 3 in Text Periodic

Periodic Signal Spectra (Chapter 3 in Text) Periodic Signal Spectra (Fourier Series) -- sum of harmonically related sinusoids Aperiodic Signals (Fourier Transform) --continuum of infinitesimal sinusoids Random (Non-Deterministic) Noise Signals --Requires a statistical interpretation We shall restrict our attention to the spectra of periodic, deterministic signals. 9/13/2021 ECE 342 (KEH) Lecture 10 1

The spectrum (frequency composition) of periodic signals is of great concern in EMC • The decomposition of the (periodic) clock signal in a digital product tells us what frequencies are generated by the product that might interfere with nearby radio receivers, etc. • For example, if the clock frequency of a product containing a microcontroller is 33. 33 MHz, its 3 rd harmonic might interfere with the operation of a nearby FM radio at a frequency of 3 x 33. 33 MHz = 100 MHz. • Therefore, we want to know the strength of the 3 rd harmonic of a specific clock waveform. We might want to change the clock frequency to 60 MHz (which has harmonics outside of the FM broadcast band), or if this is not an option, we might want to try to design the clock oscillator so that its 3 rd harmonic is suppressed. 9/13/2021 ECE 342 (KEH) Lecture 10 2

(Trigonometric) Fourier Series Analysis 9/13/2021 ECE 342 (KEH) Lecture 10 3

t, s 9/13/2021 ECE 342 (KEH) Lecture 10 4

9/13/2021 ECE 342 (KEH) Lecture 10 5

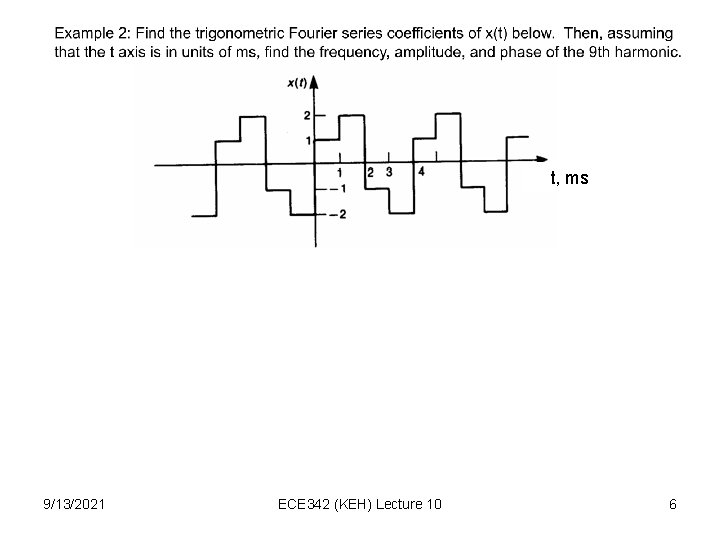
t, ms 9/13/2021 ECE 342 (KEH) Lecture 10 6

9/13/2021 ECE 342 (KEH) Lecture 10 7

9/13/2021 ECE 342 (KEH) Lecture 10 8

9/13/2021 ECE 342 (KEH) Lecture 10 9

Use of low-pass filter to reduce harmonics Consider a typical digital system clock waveform that may be approximated as a 50% duty cycle periodic square wave that takes on a value of 0 volts between 0 < t < T/2, and then changes to A volts between T/2 < t < T. (Ignoring rise and fall times. ) It is easily shown (See text equation 3. 27) that the trigonometric Fourier series for this waveform is: Thus the frequency make-up of a 50% duty cycle square wave consists of the sum of a dc (average value) term, a fundamentalfrequency sinusoid of frequency 1/T and amplitude 2 A/π, and an infinite number of odd harmonic sinusoids of frequency 3/T, 5/T, 7/T, etc. , whose amplitudes fall off as 1/n, where n is the harmonic number. 9/13/2021 ECE 342 (KEH) Lecture 10 10

9/13/2021 ECE 342 (KEH) Lecture 10 11

9/13/2021 ECE 342 (KEH) Lecture 10 12

9/13/2021 ECE 342 (KEH) Lecture 10 13