Periodic Motion Simple periodic motion is that motion





























- Slides: 37

Periodic Motion Simple periodic motion is that motion in which a body moves back and forth over a fixed path, returning to each position and velocity after a definite interval of time. Period, Period T, is the time for one complete oscillation. (seconds, s) Amplitude A Frequency, Frequency f, is the number of complete oscillations per second. Hertz (s-1)

Example 1: The suspended mass makes 30 complete oscillations in 15 s. What is the period and frequency of the motion? x F Period: T = 0. 500 s Frequency: f = 2. 00 Hz

Simple Harmonic Motion, SHM Simple harmonic motion is periodic motion in the absence of friction and produced by a restoring force that is directly proportional to the displacement and oppositely directed. x F A restoring force, F, acts in the direction opposite the displacement of the oscillating body. F = -kx

Hooke’s Law When a spring is stretched, there is a restoring force that is proportional to the displacement. F = -kx x m F The spring constant k is a property of the spring given by: k= DF Dx

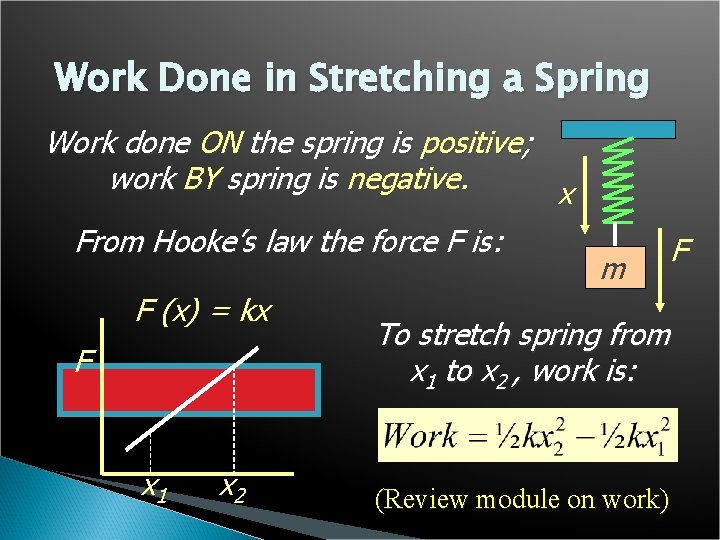
Work Done in Stretching a Spring Work done ON the spring is positive; work BY spring is negative. x From Hooke’s law the force F is: F (x) = kx F x 1 x 2 m F To stretch spring from x 1 to x 2 , work is: (Review module on work)

Example 2: A 4 -kg mass suspended from a spring produces a displacement of 20 cm. What is the spring constant? The stretching force is the weight (W = mg) of the 4 -kg mass: 20 cm F = (4 kg)(9. 8 m/s 2) = 39. 2 N F m Now, from Hooke’s law, the force constant k of the spring is: k= DF Dx = 39. 2 N 0. 2 m k = 196 N/m

Example 2(cont. : The mass m is now stretched a distance of 8 cm and held. What is the potential energy? (k = 196 N/m) The potential energy is equal to the work done in stretching the spring: 0 U = 0. 627 J 8 cm F m

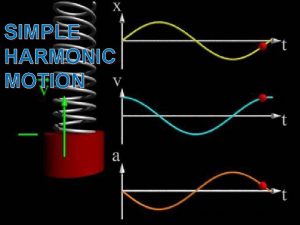
Displacement in SHM x m x = -A x=0 x = +A • Displacement is positive when the position is to the right of the equilibrium position (x = 0) and negative when located to the left. • The maximum displacement is called the amplitude A.

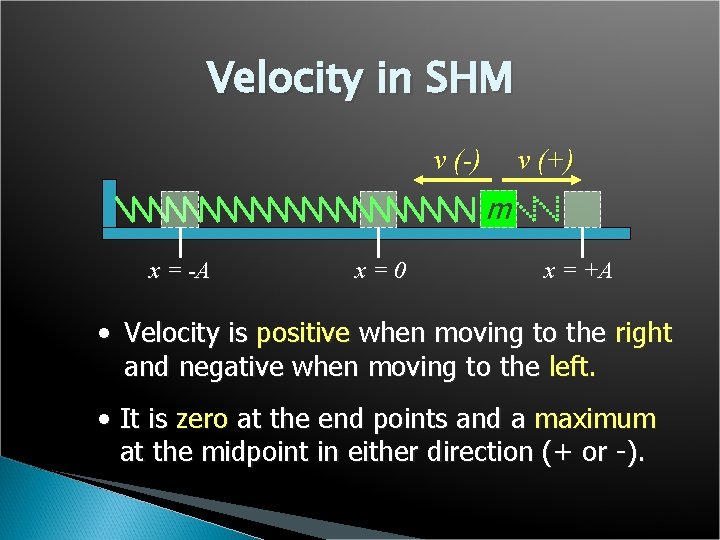
Velocity in SHM v (-) v (+) m x = -A x=0 x = +A • Velocity is positive when moving to the right and negative when moving to the left. • It is zero at the end points and a maximum at the midpoint in either direction (+ or -).

Acceleration in SHM +a -x +x -a m x = -A x=0 x = +A • Acceleration is in the direction of the restoring force. (a is positive when x is negative, and negative when x is positive. ) • Acceleration is a maximum at the end points and it is zero at the center of oscillation.

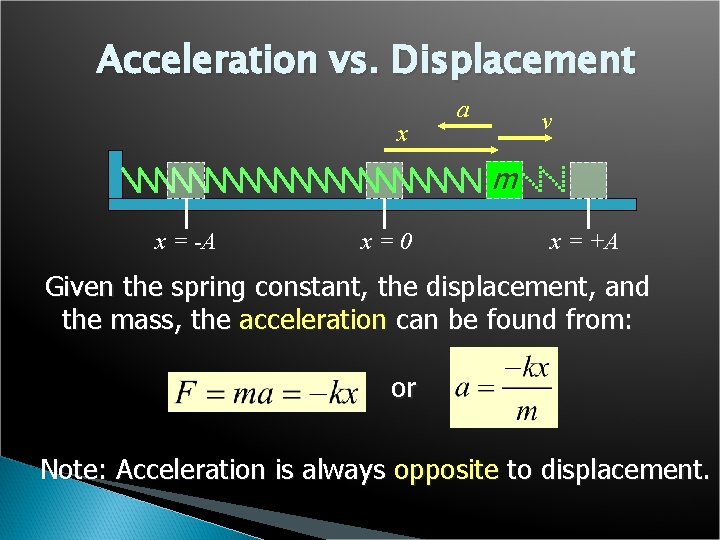
Acceleration vs. Displacement x a v m x = -A x=0 x = +A Given the spring constant, the displacement, and the mass, the acceleration can be found from: or Note: Acceleration is always opposite to displacement.

Example 3: A 2 -kg mass hangs at the end of a spring whose constant is k = 400 N/m. The mass is displaced a distance of 12 cm and released. What is the acceleration at the instant the displacement is x = +7 cm? a = -14. 0 m/s 2 a m Note: When the displacement is +7 cm (downward), the acceleration is -14. 0 m/s 2 (upward) independent of motion direction. +x

Example 4: What is the maximum acceleration for the 2 -kg mass in the previous problem? (A = 12 cm, k = 400 N/m) The maximum acceleration occurs when the restoring force is a maximum; i. e. , when the stretch or compression of the spring is largest. F = ma = -kx xmax = A m Maximum Acceleration: amax = ± 24. 0 m/s 2 +x

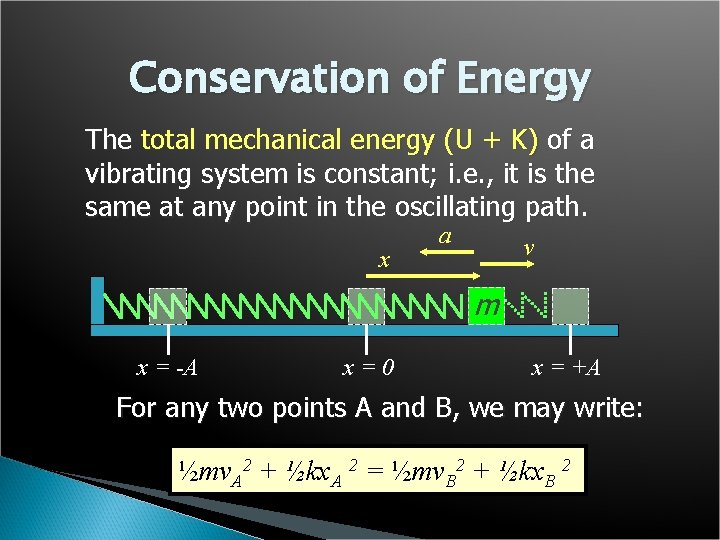
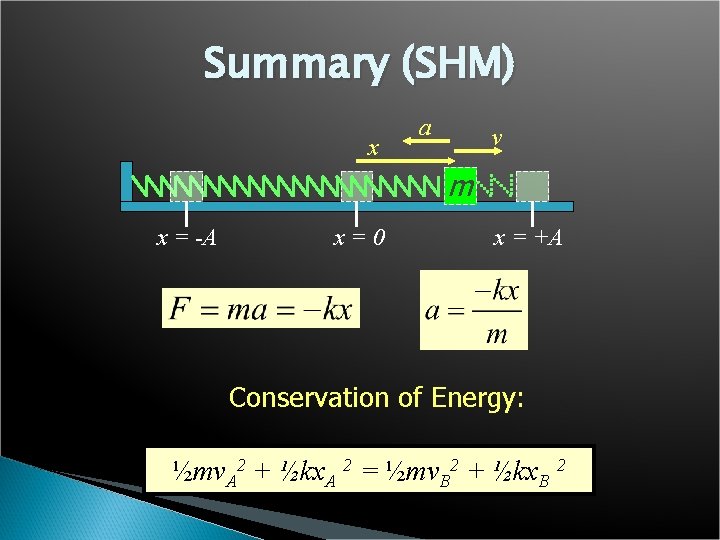
Conservation of Energy The total mechanical energy (U + K) of a vibrating system is constant; i. e. , it is the same at any point in the oscillating path. x a v m x = -A x=0 x = +A For any two points A and B, we may write: ½mv. A 2 + ½kx. A 2 = ½mv. B 2 + ½kx. B 2

Energy of a Vibrating System: A x a v m x = -A x=0 B x = +A • At points A and B, the velocity is zero and the acceleration is a maximum. The total energy is: U + K = ½k. A 2 x = A and v = 0. • At any other point: U + K = ½mv 2 + ½kx 2

Velocity as Function of Position. x a v m x = -A vmax when x = 0: x=0 x = +A

Example 5: A 2 -kg mass hangs at the end of a spring whose constant is k = 800 N/m. The mass is displaced a distance of 10 cm and released. What is the velocity at the instant the displacement is x = +6 cm? ½mv 2 + ½kx 2 = ½k. A 2 m v = ± 1. 60 m/s +x

Example 5 (Cont. ): What is the maximum velocity for the previous problem? (A = 10 cm, k = 800 N/m, m = 2 kg. ) The velocity is maximum when x = 0: 0 ½mv 2 + ½kx 2 = ½k. A 2 m v = ± 2. 00 m/s +x

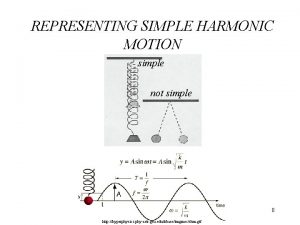
The Reference Circle The reference circle compares the circular motion of an object with its horizontal projection. x = Horizontal displacement. A = Amplitude (xmax). q = Reference angle. w = 2 f

Velocity in SHM The velocity (v) of an oscillating body at any instant is the horizontal component of its tangential velocity (v. T). v. T = w. R = w. A; w = 2 f v = -v. T sin ; = wt v = -w A sin w t v = -2 f A sin 2 f t

Acceleration Reference Circle The acceleration (a) of an oscillating body at any instant is the horizontal component of its centripetal acceleration (ac). a = -ac cos q = -ac cos(wt) R=A a = -w 2 A cos(wt)

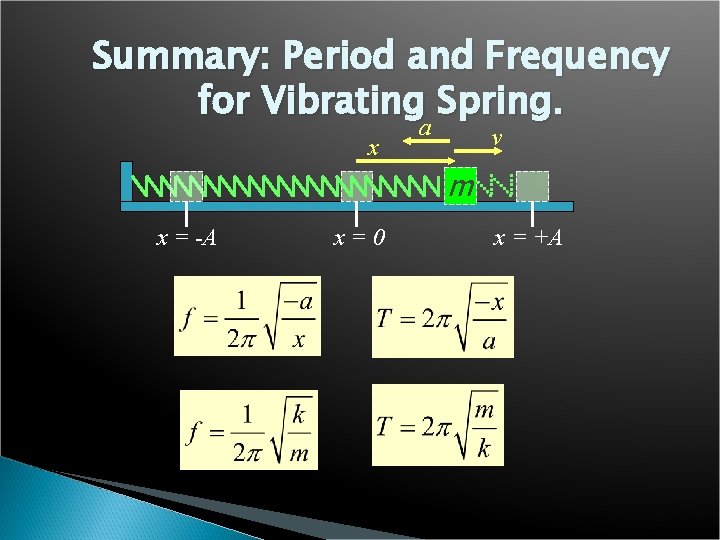
The Period and Frequency as a Function of a and x. For any body undergoing simple harmonic motion: Since a = -4 2 f 2 x and T = 1/f The frequency and the period can be found if the displacement and acceleration are known. Note that the signs of a and x will always be opposite.

Period and Frequency as a Function of Mass and Spring Constant. For a vibrating body with an elastic restoring force: Recall that F = ma = -kx: -kx The frequency f and the period T can be found if the spring constant k and mass m of the vibrating body are known. Use consistent SI units.

Example 6: The frictionless system shown below has a 2 -kg mass attached to a spring (k = 400 N/m). The mass is displaced a distance of 20 cm to the right and released. What is the frequency of the motion? x a v m x = -0. 2 m x=0 f = 2. 25 Hz x = +0. 2 m

Example 6 (Cont. ): Suppose the 2 -kg mass of the previous problem is displaced 20 cm and released (k = 400 N/m). What is the maximum acceleration? (f = 2. 25 Hz) a v x m x = -0. 2 m x=0 x = +0. 2 m Acceleration is a maximum when x = A a = 40 m/s 2

Example 6: The 2 -kg mass of the previous example is displaced initially at x = 20 cm and released. What is the velocity 2. 69 s after release? (Recall that f = 2. 25 Hz. ) a v x m v = -2 f A sin 2 f t x = -0. 2 m x = 0 x = +0. 2 m (Note: q in rads) v = -0. 916 m/s The minus sign means it is moving to the left.

Example 7: At what time will the 2 -kg mass be located 12 cm to the left of x = 0? (A = 20 cm, f = 2. 25 Hz) -0. 12 m a v x m x = -0. 2 m x = 0 t = 0. 157 s x = +0. 2 m

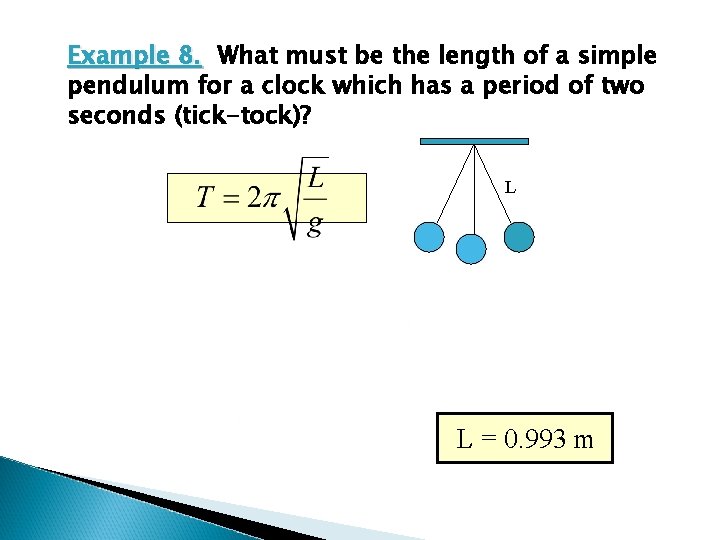
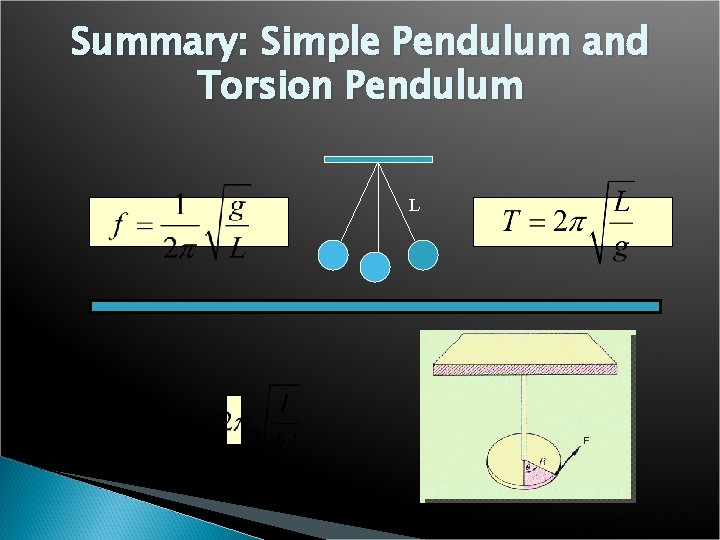
The Simple Pendulum The period of a simple pendulum is given by: L For small angles q. mg

Example 8. What must be the length of a simple pendulum for a clock which has a period of two seconds (tick-tock)? L L = 0. 993 m

The Torsion Pendulum The period T of a torsion pendulum is given by: Where k’ is a torsion constant that depends on the material from which the rod is made; I is the rotational inertia of the vibrating system.

Example 9: A 160 g solid disk is attached to the end of a wire, then twisted at 0. 8 rad and released. The torsion constant k’ is 0. 025 N m/rad. Find the period. (Neglect the torsion in the wire) For Disk: Disk I = ½m. R 2 I = ½(0. 16 kg)(0. 12 m)2 = 0. 00115 kg m 2 T = 1. 35 s Note: Period is independent of angular displacement.

Summary Simple harmonic motion (SHM) is that motion in which a body moves back and forth over a fixed path, returning to each position and velocity after a definite interval of time. The frequency (rev/s) is the reciprocal of the period (time for one revolution). x m F

Summary (Cont. ) Hooke’s Law: In a spring, there is a restoring force that is proportional to the displacement. x The spring constant k is defined by: m F

Summary (SHM) x a v m x = -A x=0 x = +A Conservation of Energy: ½mv. A 2 + ½kx. A 2 = ½mv. B 2 + ½kx. B 2

Summary (SHM)

Summary: Period and Frequency for Vibrating Spring. x a v m x = -A x=0 x = +A

Summary: Simple Pendulum and Torsion Pendulum L
 Phân độ lown
Phân độ lown Block xoang nhĩ là gì
Block xoang nhĩ là gì Thể thơ truyền thống
Thể thơ truyền thống Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Chiến lược kinh doanh quốc tế của walmart
Chiến lược kinh doanh quốc tế của walmart Tìm vết của đường thẳng
Tìm vết của đường thẳng Con hãy đưa tay khi thấy người vấp ngã
Con hãy đưa tay khi thấy người vấp ngã Tôn thất thuyết là ai
Tôn thất thuyết là ai Gây tê cơ vuông thắt lưng
Gây tê cơ vuông thắt lưng Sau thất bại ở hồ điển triệt
Sau thất bại ở hồ điển triệt Simple periodic motion
Simple periodic motion Simple harmonic motion
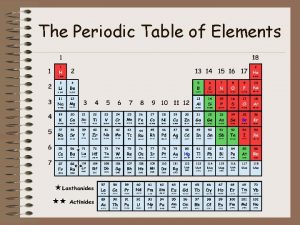
Simple harmonic motion Chapter 6 the periodic table
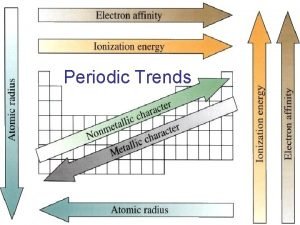
Chapter 6 the periodic table Periodic trend
Periodic trend Alien periodic table periodic trends answers
Alien periodic table periodic trends answers Chapter 6 periodic table
Chapter 6 periodic table Chapter 5 periodic law
Chapter 5 periodic law Present simple past simple future simple
Present simple past simple future simple Past simple future simple
Past simple future simple Past simple future
Past simple future Past simple present simple future simple
Past simple present simple future simple Future simple in the past
Future simple in the past Present continuous vs future simple exercises
Present continuous vs future simple exercises Swing past participle
Swing past participle Simple present forma negativa
Simple present forma negativa Future simple present simple
Future simple present simple Harmonics equations
Harmonics equations Motion periodic table
Motion periodic table Motion periodic table
Motion periodic table Motion periodic table
Motion periodic table Periodic motion
Periodic motion Periodic motion pictures
Periodic motion pictures Simple harmonic motion energy equation
Simple harmonic motion energy equation Two examples of periodic motion
Two examples of periodic motion Range of motion
Range of motion An object in motion stays in motion
An object in motion stays in motion Chapter 2 motion section 1 describing motion answer key
Chapter 2 motion section 1 describing motion answer key What is acceleration
What is acceleration