Periodic Functions These are curves based on sine

Periodic Functions

These are curves based on sine and cosine These curves fluctuate between a maximum and a minimum. • There are specific terms we must know here: 1) Crest: - top of wave - this also known as the maximum 2) Trough: - bottom of wave - this is also known as the minimum 3) Period: - from the beginning of a curve to the beginning of the next curve (one max and one min) 4) Amplitude: the height to the max/min from the axis of symmetry 5) Axis of Symmetry: a horizontal line that cuts the curve into mirror halves. Express this as y = ____. (max + min /2)

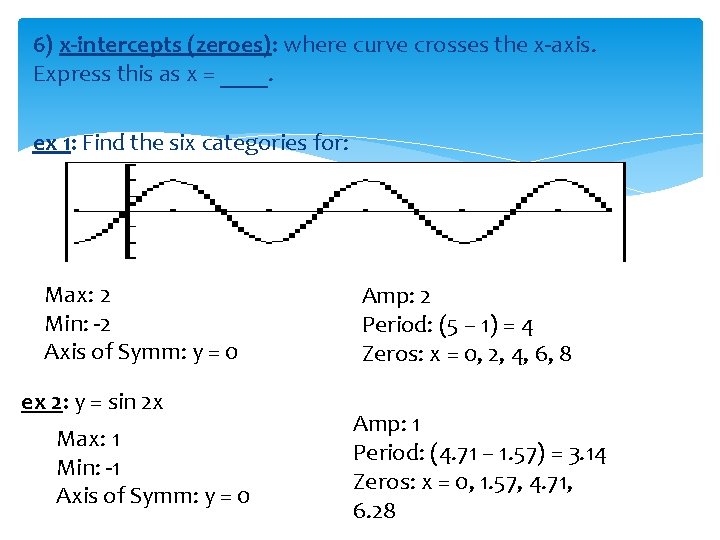
6) x-intercepts (zeroes): where curve crosses the x-axis. Express this as x = ____. ex 1: Find the six categories for: Max: 2 Min: -2 Axis of Symm: y = 0 ex 2: y = sin 2 x Max: 1 Min: -1 Axis of Symm: y = 0 Amp: 2 Period: (5 – 1) = 4 Zeros: x = 0, 2, 4, 6, 8 Amp: 1 Period: (4. 71 – 1. 57) = 3. 14 Zeros: x = 0, 1. 57, 4. 71, 6. 28

Finding Graphs from Data In order to find an equation from data, we must plug in our data into L 1 and L 2. From here we use “Sin Reg” STAT → CALC → C: Sin. Reg → Enter → L 1 → , → L 2 → , → VARS → Y-Vars → 1 → Enter This will generate a periodic equation of the form (in the y= screen): y = Asin(Bx + C) + D where A = amplitude B = period (= 2π/B) C = horizontal shift ( -ve is right, +ve is left) D = vertical shift (axis of symm/median)

From here we can graph, adjusting our window according to the question. ex: Month Temp a) b) c) d) e) J F -15 -10 M A M J J A S O N D -3 5 12 20 28 26 13 2 -10 -17 Plot a graph for 2 years Find period from equation and then in months Horizontal shift Vertical shift Write the equation

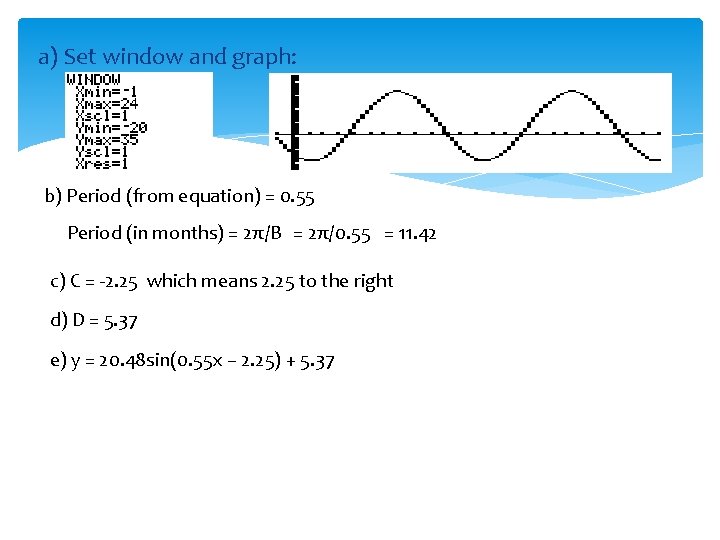
a) Set window and graph: b) Period (from equation) = 0. 55 Period (in months) = 2π/B = 2π/0. 55 = 11. 42 c) C = -2. 25 which means 2. 25 to the right d) D = 5. 37 e) y = 20. 48 sin(0. 55 x – 2. 25) + 5. 37

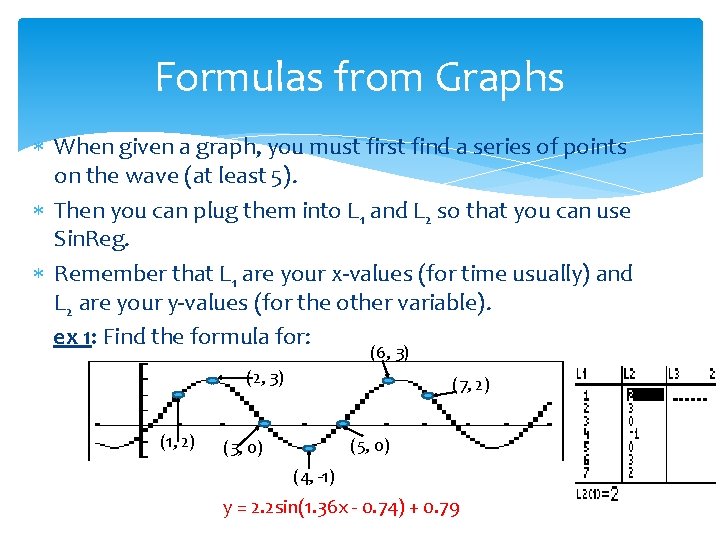
Formulas from Graphs When given a graph, you must first find a series of points on the wave (at least 5). Then you can plug them into L 1 and L 2 so that you can use Sin. Reg. Remember that L 1 are your x-values (for time usually) and L 2 are your y-values (for the other variable). ex 1: Find the formula for: (6, 3) (2, 3) (1, 2) (7, 2) (5, 0) (3, 0) (4, -1) y = 2. 2 sin(1. 36 x - 0. 74) + 0. 79

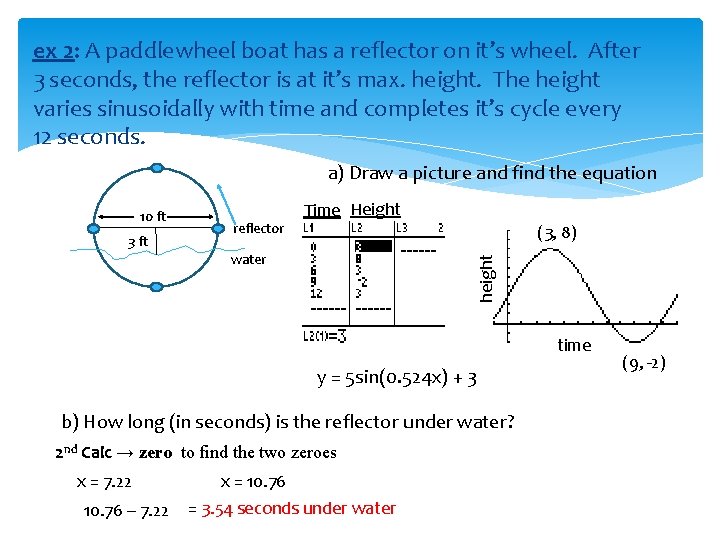
ex 2: A paddlewheel boat has a reflector on it’s wheel. After 3 seconds, the reflector is at it’s max. height. The height varies sinusoidally with time and completes it’s cycle every 12 seconds. a) Draw a picture and find the equation 10 ft 3 ft reflector Time Height (3, 8) height water time y = 5 sin(0. 524 x) + 3 b) How long (in seconds) is the reflector under water? 2 nd Calc → zero to find the two zeroes x = 7. 22 10. 76 – 7. 22 x = 10. 76 = 3. 54 seconds under water (9, -2)

When Asked… When given a formula and asked to find: 1) Something on the y-axis (gives you an x-value): - 2 nd trace → 1: value (enter the number from question) **give the y-value for the answer** 2) Something on the x-axis (gives you a y-value): - go into y= and plug that value into y 2 - graph - 2 nd trace → 5: intersect **give the x-value for the answer**

Window Settings for Formulas x-min: 0 x-max: read question x-scl: set this according to the x-max (usually 1 unless dealing with hundreds/thousands) y-min: D - A y-max: D + A