Perimeter Area 6 th Grade Geometry By Ms

Perimeter & Area 6 th Grade Geometry By: Ms. Candra Bryant

Aim of the Lesson: n n n This is a lesson in perimeter and area using a power point presentation. This lesson teaches how to cut “complex” shapes apart into “more simple” shapes to find the area. That is, it teaches that the area of a big shape is equal to the sum of the area of smaller shapes that make it up.

Reminders n What Does The Dictionary Say? What is the Perimeter of a polygon? n What is the Area of a polygon? n What about Circles? n A circle doesn’t have a perimeter, it has a Circumference. n Is the Area the same as in a polygon? n

Reminders Continued n We’ve already covered how to find the perimeters and areas of “simple shapes, ” but lets go over it one last time. n n n Squares & Rectangles Triangles Circles

Perimeters of More Complicated Shapes n n n To find the perimeter of any shape, all you do is add of the lengths of all of the sides of that shape. This works if the shape has three sides, or 1, 000 sides. As long as you remember how to add, you can find the perimeter of any shape.

Areas of More Complicated Shapes n n n Area is a little more tricky than perimeter. There are many formulas that you can memorize to find the areas of different shapes, but that’s not what this lesson is about. Here, we will learn how to find the areas of different shapes when we don’t have its formula memorized.

How Can We Find Areas? One way of finding the area of a shape is to cut it apart. n All we have to do is cut the shape into pieces that we already know how to find the areas of n n Squares, Rectangles, Triangles, and Circles.

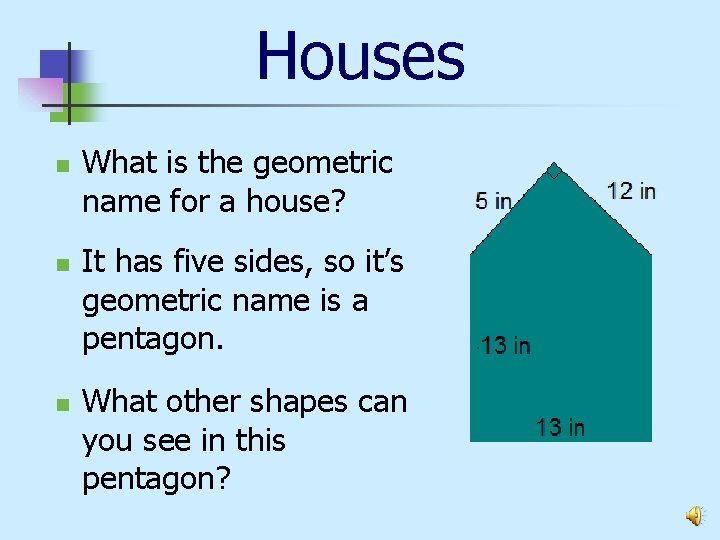
Houses n n n What is the geometric name for a house? It has five sides, so it’s geometric name is a pentagon. What other shapes can you see in this pentagon?

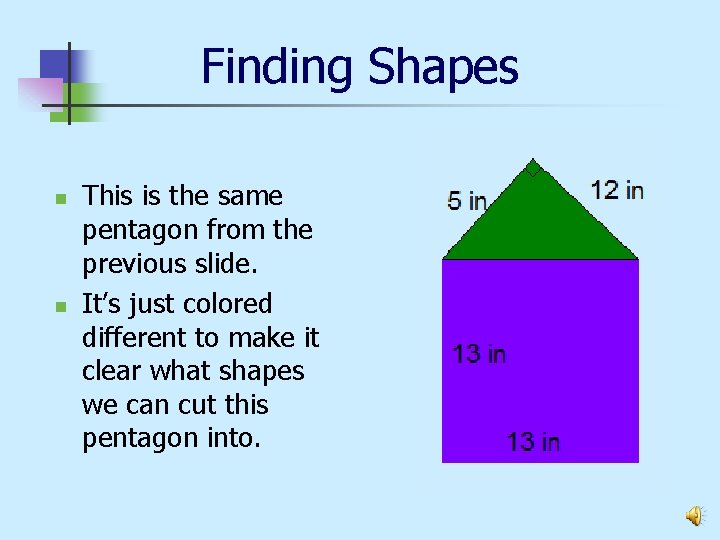
Finding Shapes n n This is the same pentagon from the previous slide. It’s just colored different to make it clear what shapes we can cut this pentagon into.

Cutting It Apart n n Now, instead of a pentagon, we have a right triangle and a square. We already know how to find the areas of these shapes.

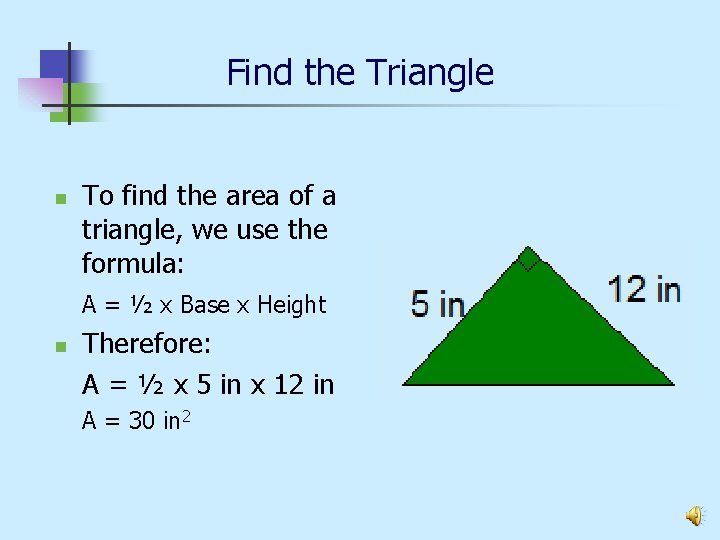
Find the Triangle n To find the area of a triangle, we use the formula: A = ½ x Base x Height n Therefore: A = ½ x 5 in x 12 in A = 30 in 2

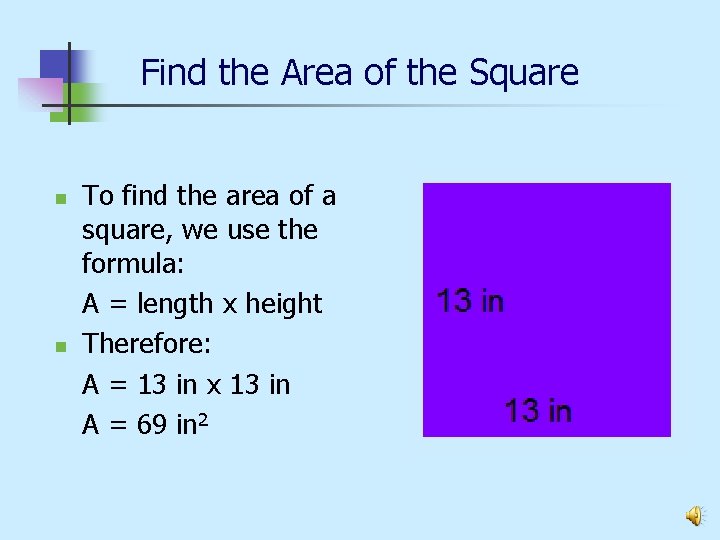
Find the Area of the Square n n To find the area of a square, we use the formula: A = length x height Therefore: A = 13 in x 13 in A = 69 in 2

Find the Area of the Pentagon n n Now, add the area of the triangle, to the area of the square, and you’ll have the area of the pentagon. 30 in 2 + 69 in 2 = 99 in 2

Practice What You’ve Learned n n That’s the end of this lesson, now it’s time to practice what you’ve learned. Here’s a worksheet to practice what you’ve learned. You may need to use the Pythagorean Theorem on this worksheet. If you don’t remember how that works, check out Worksheet with Answers