Performance Task Functions and Everyday Situations http map

Performance Task Functions and Everyday Situations http: //map. mathshell. org/materials/index. php

Comparing Traditional and Common Core Instruction Function Common Core Traditional Definition Table Mapping Vertical Line Test

x f(x) Sample Lesson on Function Traditional y

Function - Definition A function is a relation in which the members of the domain (xvalues) DO NOT repeat. So, for every x-value there is only one yvalue that corresponds to it. Y-values can be repeated. How do these lessons ensure students understand functions?

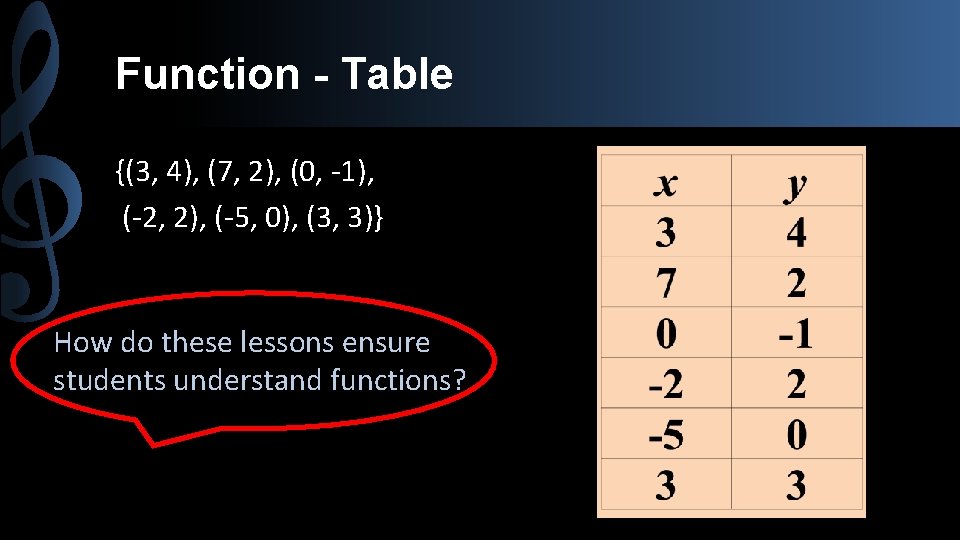
Function - Table {(3, 4), (7, 2), (0, -1), (-2, 2), (-5, 0), (3, 3)} How do these lessons ensure students understand functions?

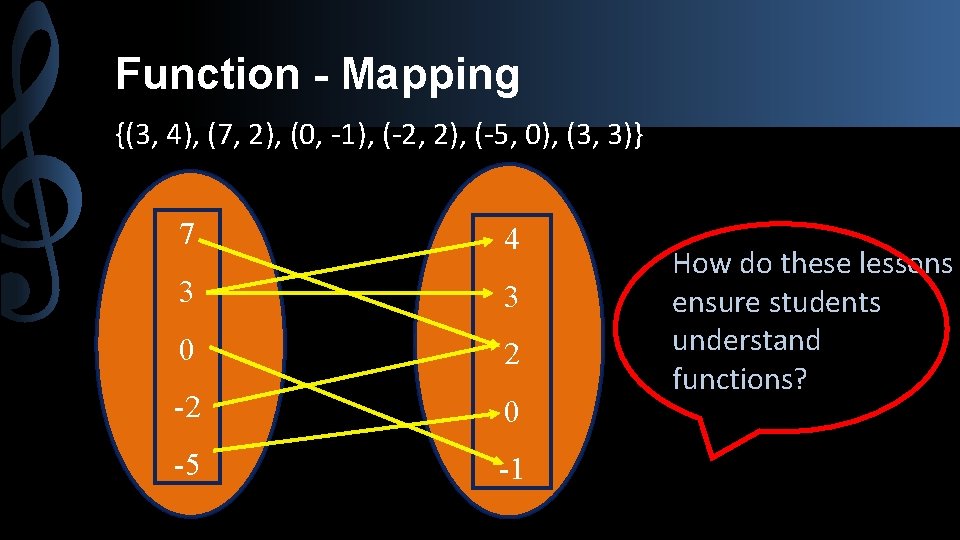
Function - Mapping {(3, 4), (7, 2), (0, -1), (-2, 2), (-5, 0), (3, 3)} 7 4 3 3 0 2 -2 0 -5 -1 How do these lessons ensure students understand functions?

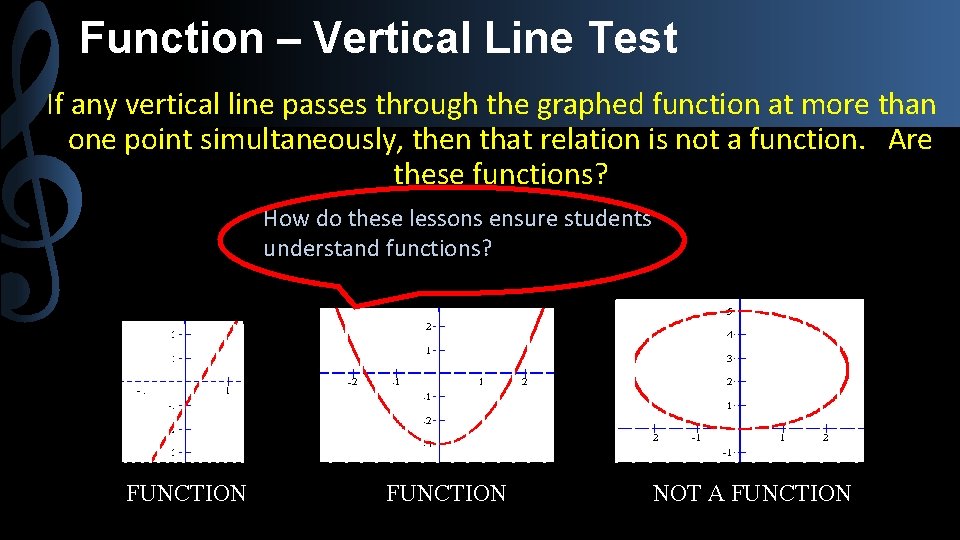
Function – Vertical Line Test If any vertical line passes through the graphed function at more than one point simultaneously, then that relation is not a function. Are these functions? How do these lessons ensure students understand functions? FUNCTION NOT A FUNCTION

x f(x) Sample Lesson on Function Common Core y

Common Core Math Standards Practice Standards Content Standards

Today’s Common Core Math Practices MP MP 1 1 M M 2 MP 4 MP 5 Make sense of problems and persevere in solving them. Reason abstractly and quantitatively Model with Mathematics Use appropriate tools strategically

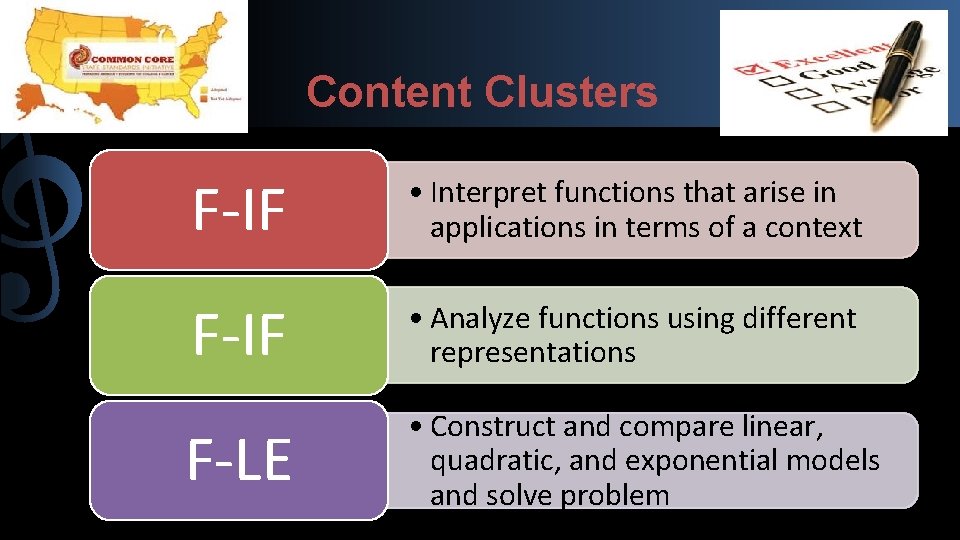
Content Clusters F-IF • Interpret functions that arise in applications in terms of a context F-IF • Analyze functions using different representations F-LE • Construct and compare linear, quadratic, and exponential models and solve problem

Unwrap the Standards F-IF. 4 • For a function that models a relationship between two quantities, interpret key features of graphs and tables in term of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity. (Understand, 2), (Apply, 2)

Creating a Pathway to our Bloom’s/DOK Identified Level Revised Bloom’s Taxonomy Webb’s DOK Level 1 Recall & Reproduction Remember Retrieve knowledge from long-term memory, recognize, recall, locate, identify o Understand Construct meaning, clarify, paraphrase, represent, translate, illustrate, give examples, classify, categorize, summarize, generalize, infer a logical conclusion (such as from examples given), predict, compare/contrast, match like ideas, explain, construct models o o o Webb’s DOK Level 2 Skills & Concepts Webb’s DOK Level 3 Strategic Thinking/ Reasoning Webb’s DOK Level 4 Extended Thinking Recall, observe, & recognize facts, principles, properties Recall/ identify conversions among representations or numbers (e. g. , customary and metric measures) Evaluate an expression Locate points on a grid or number on number line Solve a one-step problem Represent math relationships in words, pictures, or symbols Read, write, compare decimals in scientific notation o o o o Apply Carry out or use a procedure in a given situation; carry out (apply to a familiar task), or use (apply) to an unfamiliar task o o o Follow simple procedures (recipe-type directions) Calculate, measure, apply a rule (e. g. , rounding) Apply algorithm or formula (e. g. , area, perimeter) Solve linear equations Make conversions among representations or numbers, or within and between customary and metric measures o o o Analyze Break into constituent parts, determine how parts relate, differentiate between relevant-irrelevant, distinguish, focus, select, organize, outline, find coherence, deconstruct o o o Evaluate Make judgments based on criteria, check, detect inconsistencies or fallacies, judge, critique Create Reorganize elements into new patterns/structures, generate, hypothesize, design, plan, construct, produce o Retrieve information from a table or graph to answer a question Identify whether specific information is contained in graphic representations (e. g. , table, graph, T-chart, diagram) Identify a pattern/trend o o o Specify and explain relationships (e. g. , nonexamples/examples; cause-effect) Make and record observations Explain steps followed Summarize results or concepts Make basic inferences or logical predictions from data/observations Use models /diagrams to represent or explain mathematical concepts Make and explain estimates o o Select a procedure according to criteria and perform it Solve routine problem applying multiple concepts or decision points Retrieve information from a table, graph, or figure and use it solve a problem requiring multiple steps Translate between tables, graphs, words, and symbolic notations (e. g. , graph data from a table) Construct models given criteria o Categorize, classify materials, data, figures based on characteristics Organize or order data Compare/ contrast figures or data Select appropriate graph and organize & display data Interpret data from a simple graph Extend a pattern Use concepts to solve non-routine problems Explain, generalize, or connect ideas using supporting evidence Make and justify conjectures Explain thinking when more than one response is possible Explain phenomena in terms of concepts o Design investigation for a specific purpose or research question Conduct a designed investigation Use concepts to solve non-routine problems Use & show reasoning, planning, and evidence Translate between problem & symbolic notation when not a direct translation o o Select or devise approach among many alternatives to solve a problem Conduct a project that specifies a problem, identifies solution paths, solves the problem, and reports results o o o Compare information within or across data sets or texts Analyze and draw conclusions from data, citing evidence Generalize a pattern Interpret data from complex graph Analyze similarities/differences between procedures or solutions o o o Analyze multiple sources of evidence analyze complex/abstract themes Gather, analyze, and evaluate information o Cite evidence and develop a logical argument for concepts or solutions Describe, compare, and contrast solution methods Verify reasonableness of results o Gather, analyze, & evaluate information to draw conclusions Apply understanding in a novel way, provide argument or justification for the application Synthesize information within one data set, source, or text Formulate an original problem given a situation Develop a scientific/mathematical model for a complex situation o o o o o Brainstorm ideas, concepts, or perspectives related to a topic o Generate conjectures or hypotheses based on observations or prior knowledge and experience o o Relate mathematical or scientific concepts to other content areas, other domains, or other concepts Develop generalizations of the results obtained and the strategies used (from investigation or readings) and apply them to new problem situations Synthesize information across multiple sources or texts Design a mathematical model to inform and solve a practical or abstract situation 13

Before the Lesson HANDOUTS # 4 Students work individually on this task that is designed to reveal their current understanding and difficulties. Review the solutions and create questions for students to consider to improve their learning

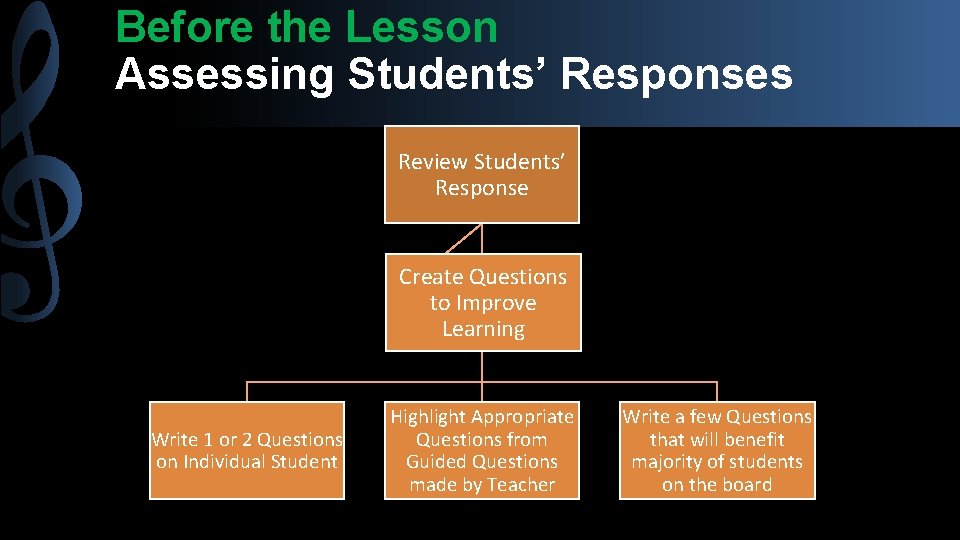
Before the Lesson Assessing Students’ Responses Review Students’ Response Create Questions to Improve Learning Write 1 or 2 Questions on Individual Student Highlight Appropriate Questions from Guided Questions made by Teacher Write a few Questions that will benefit majority of students on the board

Create Questions to Improve Learning Common Issues Guided Questions • Draws continuous lines for all the graphs • Cut the axes at inappropriate places • Draws a graph that consists of two straight lines of different slopes • Unable to interpret and use the formulas correctly • Is X a discrete or continuous variable? Why? • How many passengers would you need for Y=0? • Why does the steepness of your slope change? • What does each statement tell you about the value of X and value of Y?

Whole-Class Introduction Give each student a mini-whiteboard, a pen, and eraser. Ask students to sketch a graph that describes this situation. Can you sketch a graph to show y will depend on x?

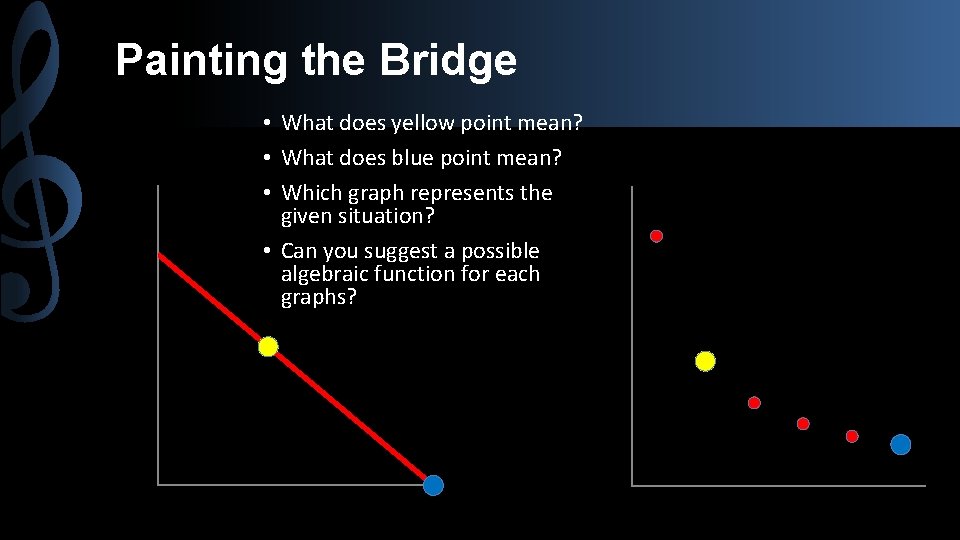
Painting the Bridge • What does yellow point mean? • What does blue point mean? • Which graph represents the given situation? • Can you suggest a possible algebraic function for each graphs? Time Number of Workers

Support Understanding Academic Language – Layered Book

Additional Instructional Strategies for Academic Language – Frayer’s Model Definition Characteristics A function is a relation in which each element of the domain is paired with exactly one element of the range. Another way of saying it is that there is one and only one output (y) with each input (x). Examples Function Non-Examples

Today’s Lesson

During the Lesson: Matching Situation to Graph 1 • Organize the class into Groups of two or three students. 2 • Students take turns to match situation card to the sketched graphs. Explain their thinking so everyone in the group will agree. Complete the two blank graphs! 3 • Arrange pairs side by side so the teacher could check the understanding. Question students to help any misconceptions.

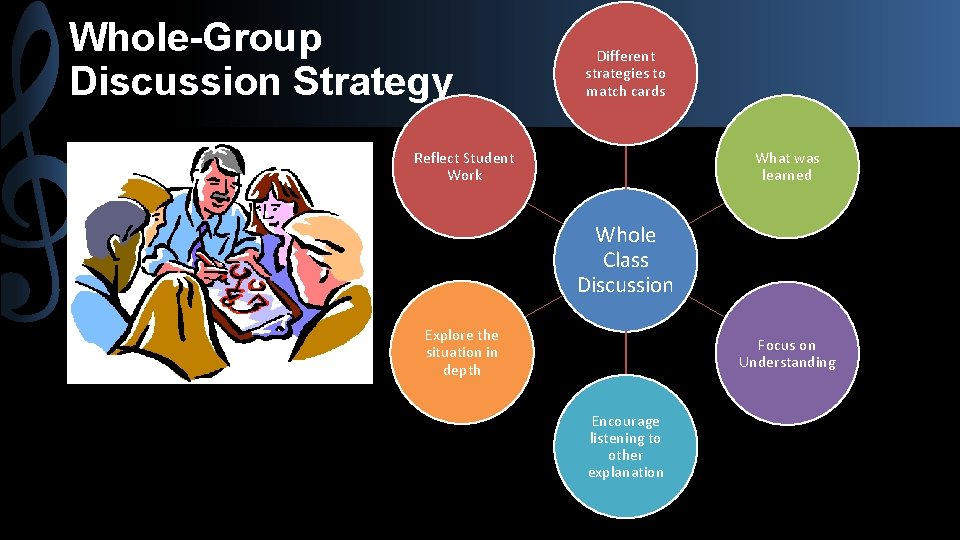
Whole-Group Discussion Strategy Different strategies to match cards Reflect Student Work What was learned Whole Class Discussion Explore the situation in depth Focus on Understanding Encourage listening to other explanation

During the Lesson: Matching Situation and Graphs to Formulas 4 5 6 7 • When students have had a chance to match the situations and graphs, give each group the cut up cards: Algebraic Functions, a large sheet of paper, and glue stick for making a poster • Match these cards to the pairs that already have on the table without calculator. • After matching the function, try to answer the question on the right hand side of the situation card. • Allow students to check their answers using calculators.

After the Lesson HANDOUT # 5 Student will do the “Another Four Situations” Check students’ understanding of functions and their types such as continuous or discrete functions

the Everyday Situation Write a Function Story Graph the Function Story and provide the rational. Use academic vocabulary that was learned during the lesson. Discuss the work with your elbow partner. In the Learning Log, describe the difference between graphs of functions and non-functions with examples.

What is Common Core Instruction? Before the Lesson Activity: Check Student Learning During the Lesson: Teaching the Concept with Math Practices After the Lesson: Check for Student Understanding

Let’s compare Traditional vs Common Core Practice Topic: Algebra 1 - Interpreting Functions Traditional • Skilled Based Learning • Drill and Rote Memory • Teacher as Lecturer • What else? CCSS • Concept Based Learning • Apply to Everyday Situation (which requires greater understanding) • Teacher as Facilitator • What else?

Reflect on the Lesson based on Using and Citing Evidence What went well with the lesson? Did the lesson go as envisioned? How did the students respond, in their attitudes and their discussion? What will you do differently next time? How might the structure and pedagogy of the common core lesson carry over to other lessons?

PD Evaluation