Performance Measures x x and x x Quantum

Performance Measures x. x, and x. x Quantum Monte Carlo studies of metals and materials with properties determined by weak dispersive interactions Randolph Q. Hood Physical Sciences Lawrence Livermore National Laboratory

Weak dispersive interaction ++ - ++-++ - - + ++ + +-+-+ -+- Quantum mechanically induced dipoles type of van der Waals interaction Important in life processes such as genetic replication and proteins, and for several types of proposed H 2 storage Physical Sciences 2

Weak dispersive interaction neglected in mean field DFT typically predicts accurate structures, but • van der Waals not included in mean field DFT • LDA & GGA qualitatively disagree on binding • Need “beyond DFT” approaches Quantum Monte Carlo gives correct description of van der Waals interactions Physical Sciences 3

Overview § Describe quantum Monte Carlo – DMC § Argon – dimers, trimers, and FCC solid phase § Applications for H 2 storage. H 2 on carbon absorbents benzene, coronene, and graphene § Applications in metals, FCC aluminum Physical Sciences 4

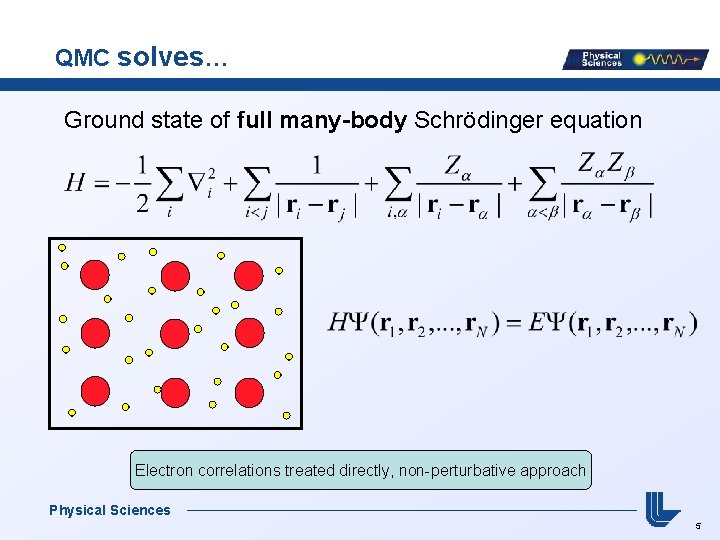
QMC solves… Ground state of full many-body Schrödinger equation Electron correlations treated directly, non-perturbative approach Physical Sciences 5

Variational Monte Carlo (VMC) Slater-Jastrow trial wavefunction Single particle orbitals from DFT and parameters in are determined using variance minimization Physical Sciences 6

DFT inputs for “production” runs • PWSCF • LDA & GGA exchange-correlation functionals • Plane wave basis sets (150 - 400 Rydberg cutoff) • Norm-conserving, Troullier-Martins pseudopotentials (Casula scheme to maintain variational principle) • Experimental structures (no optimization) Physical Sciences 7

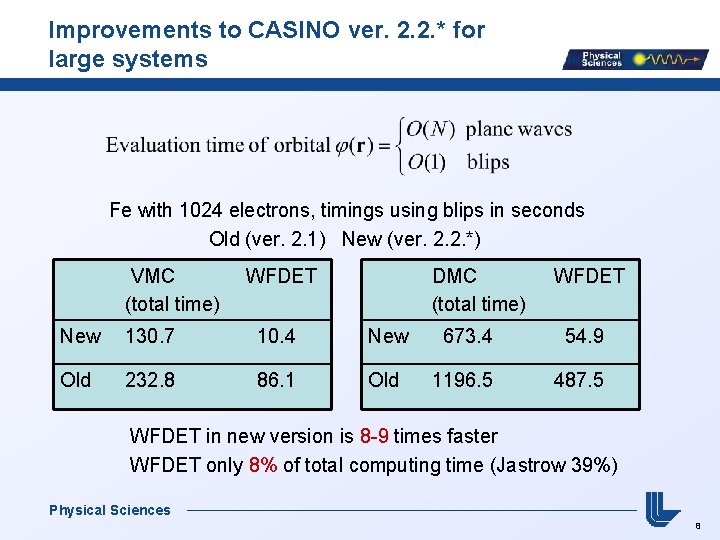
Improvements to CASINO ver. 2. 2. * for large systems Fe with 1024 electrons, timings using blips in seconds Old (ver. 2. 1) New (ver. 2. 2. *) VMC (total time) WFDET DMC (total time) WFDET New 130. 7 10. 4 New 673. 4 54. 9 Old 232. 8 86. 1 Old 1196. 5 487. 5 WFDET in new version is 8 -9 times faster WFDET only 8% of total computing time (Jastrow 39%) Physical Sciences 8

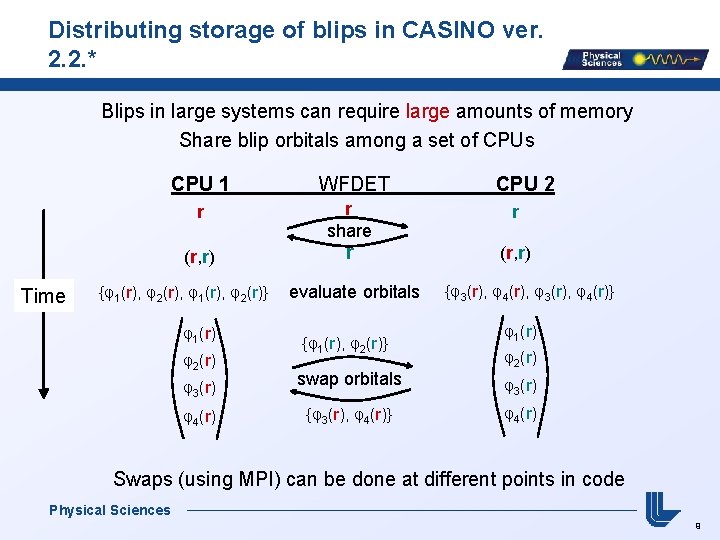
Distributing storage of blips in CASINO ver. 2. 2. * Blips in large systems can require large amounts of memory Share blip orbitals among a set of CPUs Time CPU 1 WFDET r r share r (r, r) {φ1(r), φ2(r), φ1(r), φ2(r)} φ1(r) φ2(r) φ3(r) φ4(r) evaluate orbitals {φ1(r), φ2(r)} swap orbitals {φ3(r), φ4(r)} CPU 2 {φ3(r), φ4(r), φ3(r), φ4(r)} φ1(r) φ2(r) φ3(r) φ4(r) Swaps (using MPI) can be done at different points in code Physical Sciences 9

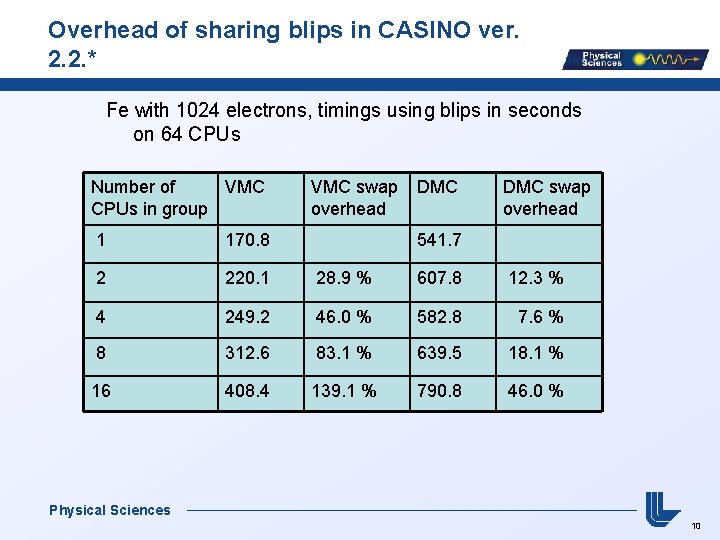
Overhead of sharing blips in CASINO ver. 2. 2. * Fe with 1024 electrons, timings using blips in seconds on 64 CPUs Number of VMC CPUs in group VMC swap overhead DMC swap overhead 1 170. 8 541. 7 2 220. 1 28. 9 % 607. 8 12. 3 % 4 249. 2 46. 0 % 582. 8 7. 6 % 8 312. 6 83. 1 % 639. 5 18. 1 % 16 408. 4 139. 1 % 790. 8 46. 0 % Physical Sciences 10

FCC argon bound by weak dispersion interactions • Argon (closed electronic shell) very inert • Noble atom solid, argon melts at 84 K • Well characterized experimentally FCC argon Physical Sciences 11

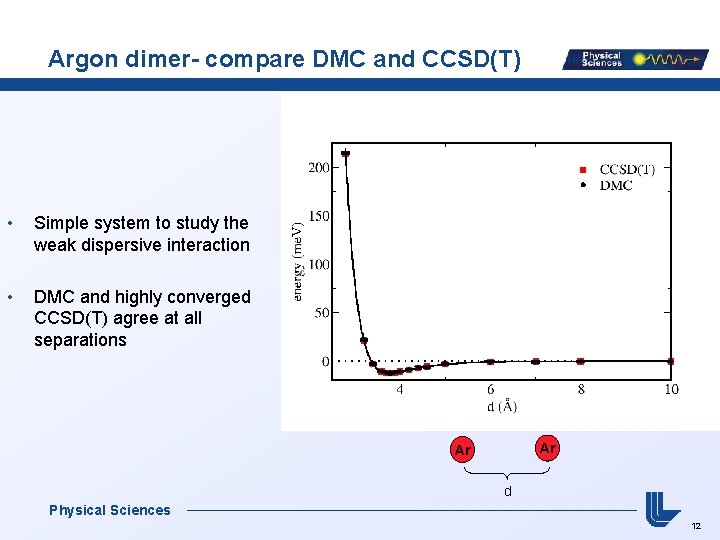
Argon dimer- compare DMC and CCSD(T) • Simple system to study the weak dispersive interaction • DMC and highly converged CCSD(T) agree at all separations Ar Ar d Physical Sciences 12

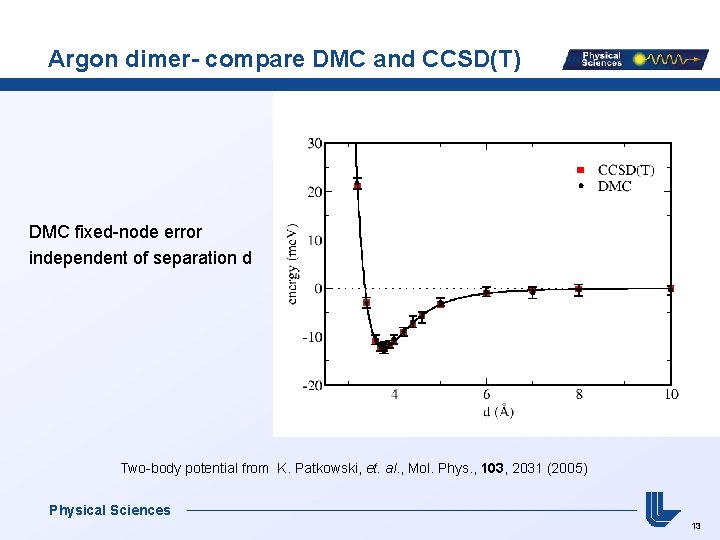
Argon dimer- compare DMC and CCSD(T) DMC fixed-node error independent of separation d Two-body potential from K. Patkowski, et. al. , Mol. Phys. , 103, 2031 (2005) Physical Sciences 13

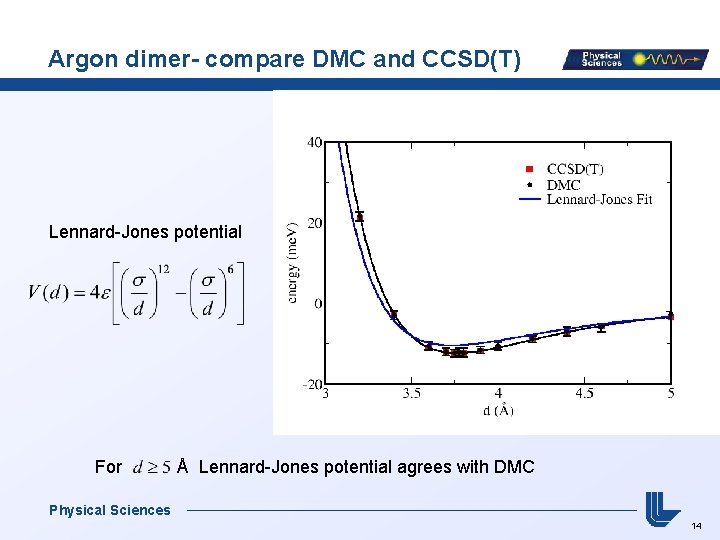
Argon dimer- compare DMC and CCSD(T) Lennard-Jones potential For Å Lennard-Jones potential agrees with DMC Physical Sciences 14

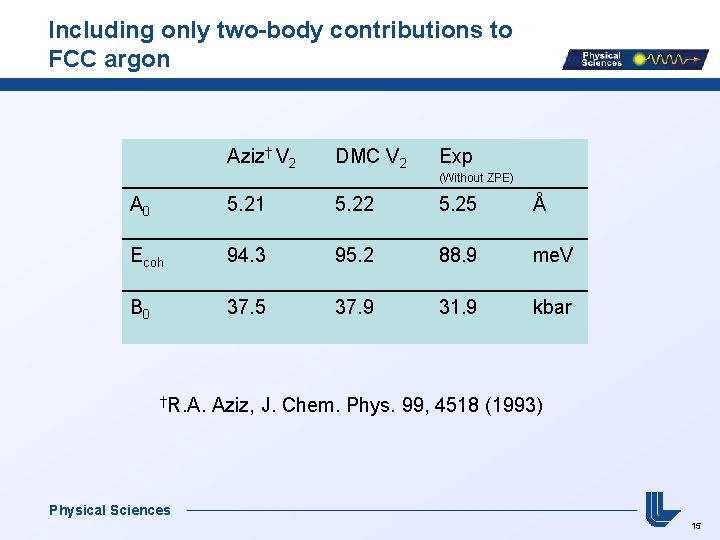
Including only two-body contributions to FCC argon Aziz† V 2 DMC V 2 Exp (Without ZPE) A 0 5. 21 5. 22 5. 25 Å Ecoh 94. 3 95. 2 88. 9 me. V B 0 37. 5 37. 9 31. 9 kbar †R. A. Aziz, J. Chem. Phys. 99, 4518 (1993) Physical Sciences 15

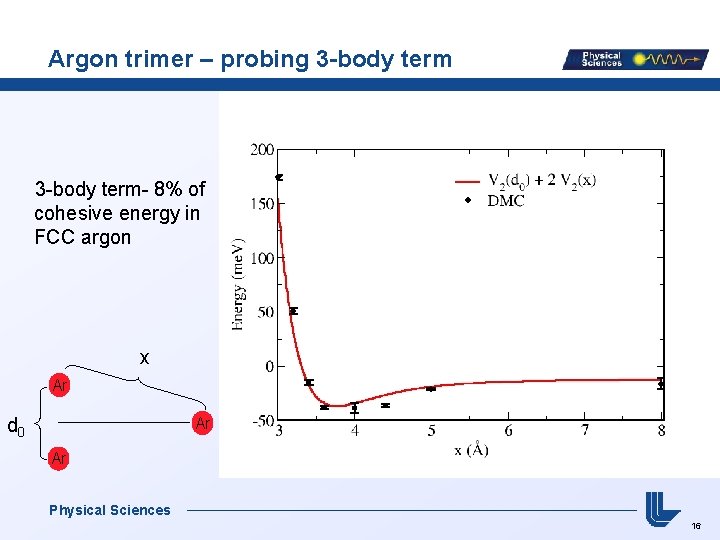
Argon trimer – probing 3 -body term- 8% of cohesive energy in FCC argon x Ar d 0 Ar Ar Physical Sciences 16

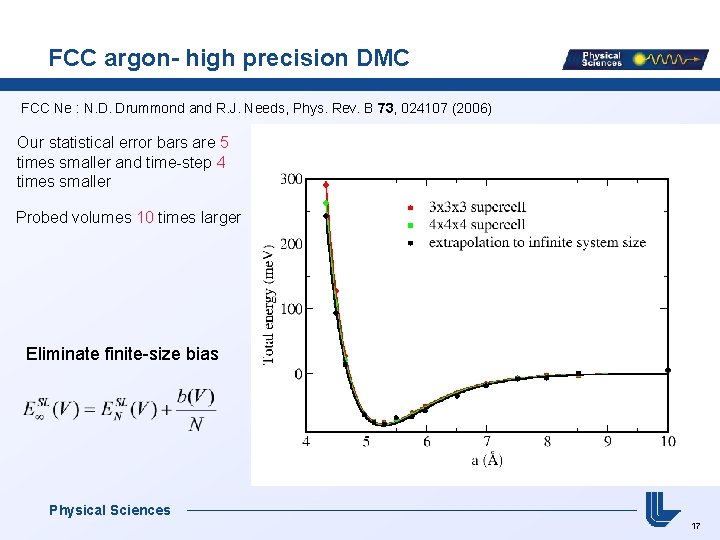
FCC argon- high precision DMC FCC Ne : N. D. Drummond and R. J. Needs, Phys. Rev. B 73, 024107 (2006) Our statistical error bars are 5 times smaller and time-step 4 times smaller Probed volumes 10 times larger Eliminate finite-size bias Physical Sciences 17

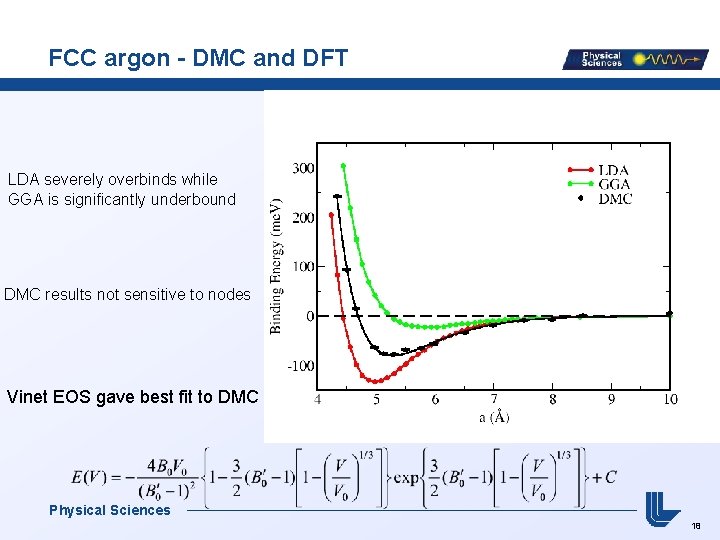
FCC argon - DMC and DFT LDA severely overbinds while GGA is significantly underbound DMC results not sensitive to nodes Vinet EOS gave best fit to DMC Physical Sciences 18

FCC argon – comparison with experiment LDA GGA DMC Exp (Without ZPE) A 0 5. 0 6. 0 5. 28(2) 5. 25 Å Ecoh 140 22 79(2) 88. 9 me. V/atom B 0 61 3. 7 31(1) 31. 9 kbar error of 10 me. V/atom = 0. 2 kcal/mole sub-chemical accuracy error 2. 0 kcal/mole Variational principle – get better cancellation of fixed-node error by computing EOS Physical Sciences 19

Fixed-node error in DMC Binding energies in semiconductors (e. V/atom) Si Ge C LDA 5. 28 4. 59 8. 61 DMC 4. 63(2) 3. 85(2) 7. 46(1) Exp. 4. 62(2) 3. 85 7. 37 Binding energies in molecules 55 molecules (G 1 basis set) DMC error =130 me. V/atom = 2. 9 kcal/mole J. C. Grossman, J. Chem. Phys. 117, 1434 (2002) Computing binding energies using EOS approach would likely give sub-chemical accuracy Physical Sciences 20

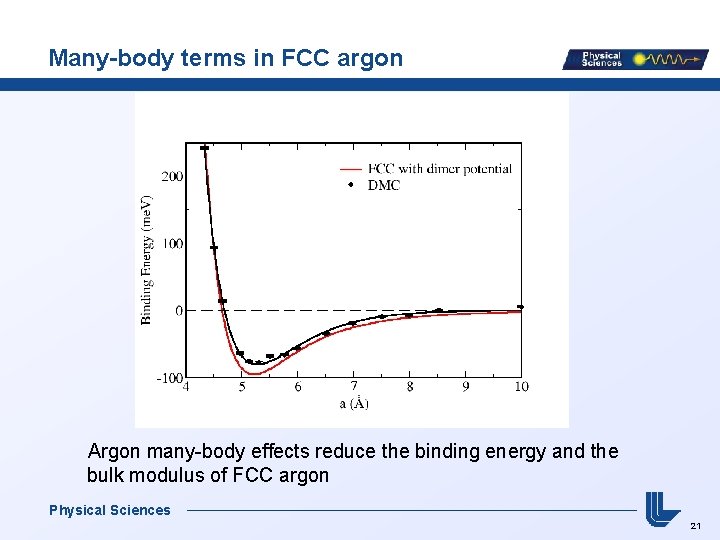
Many-body terms in FCC argon Argon many-body effects reduce the binding energy and the bulk modulus of FCC argon Physical Sciences 21

Hydrogen economy requires effective hydrogen storage • Ideal storage is at room temperature • High density requires non-hydrogen elements (1 liter gasoline has 64% more H than 1 liter of liquid H) • Range of H 2 binding energies suitable: 0. 1 - 0. 5 e. V/(H 2 molecule) BMW Hydrogen 7 Physical Sciences 22

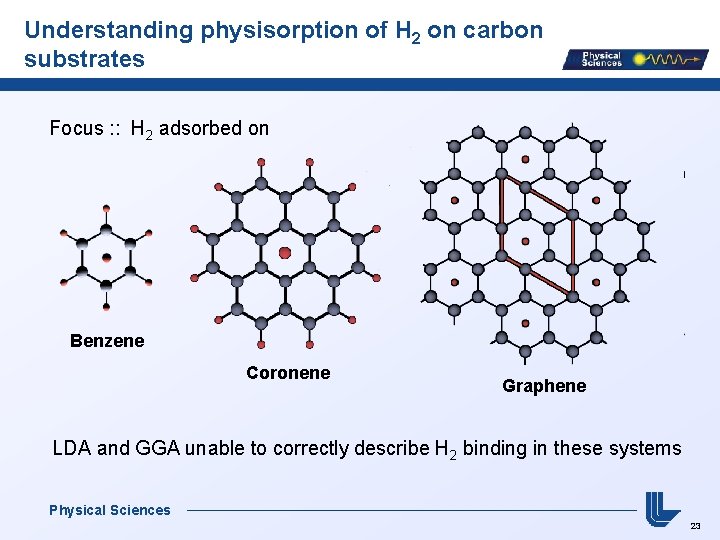
Understanding physisorption of H 2 on carbon substrates Focus : : H 2 adsorbed on Benzene Coronene Graphene LDA and GGA unable to correctly describe H 2 binding in these systems Physical Sciences 23

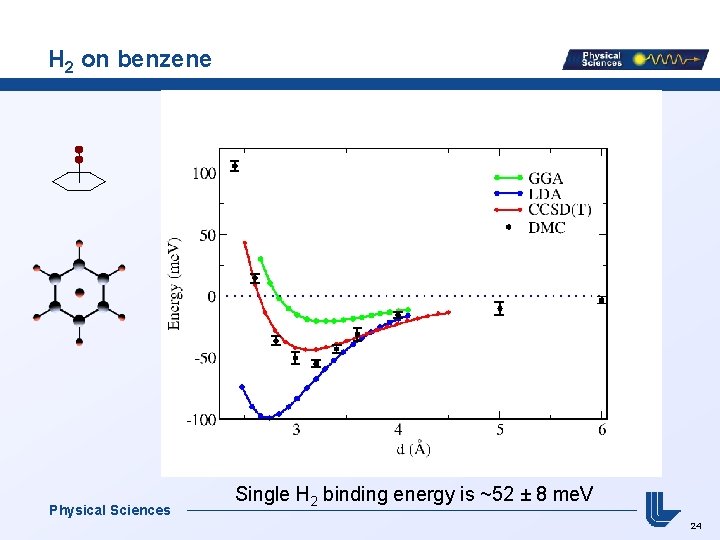
H 2 on benzene Physical Sciences Single H 2 binding energy is ~52 ± 8 me. V 24

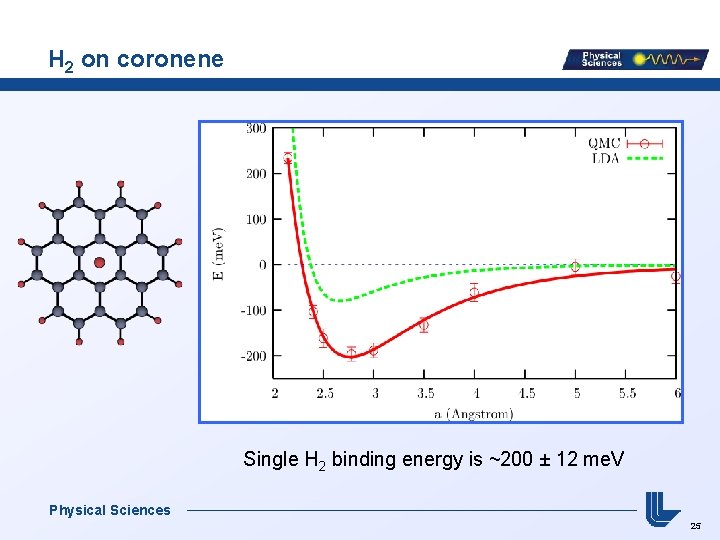
H 2 on coronene Single H 2 binding energy is ~200 ± 12 me. V Physical Sciences 25

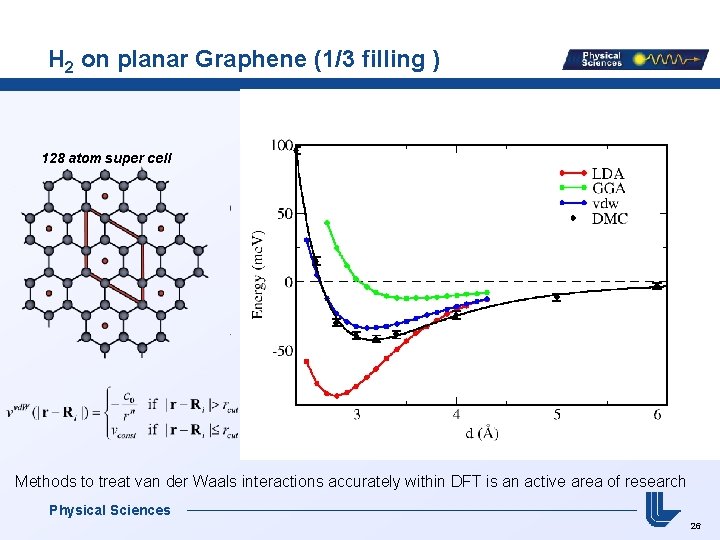
H 2 on planar Graphene (1/3 filling ) 128 atom super cell Methods to treat van der Waals interactions accurately within DFT is an active area of research Physical Sciences 26

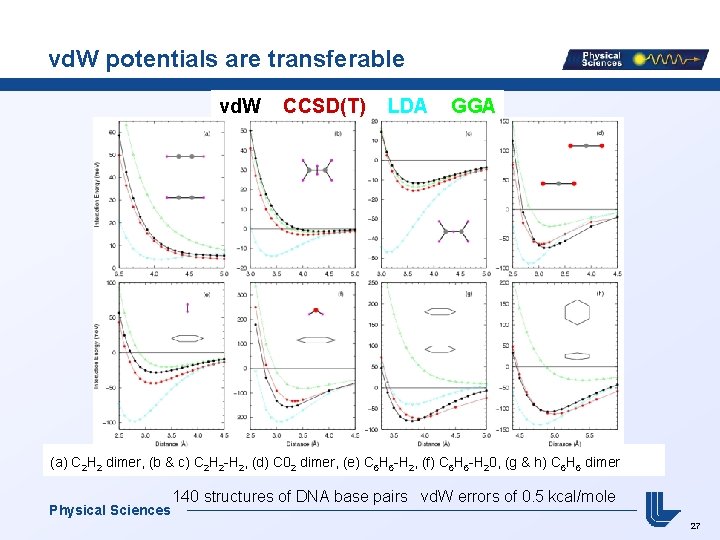
vd. W potentials are transferable vd. W CCSD(T) LDA GGA (a) C 2 H 2 dimer, (b & c) C 2 H 2 -H 2, (d) C 02 dimer, (e) C 6 H 6 -H 2, (f) C 6 H 6 -H 20, (g & h) C 6 H 6 dimer Physical Sciences 140 structures of DNA base pairs vd. W errors of 0. 5 kcal/mole 27

In progress / future directions • Carbon based materials offer many possibilities for tuning binding energetics of H 2 • curvature, damage, doping, decorating, charging • Metal-organic frameworks (MOFs) have shown promise for H 2 storage Physical Sciences 28

Applying DMC to metals First important application of DMC to electronic systems was homogeneous electron gas at LLNL (D. M Ceperley and B. J. Alder, Phys. Rev. Lett. 45, 566 (1980)) § Third most cited Physical Review Letters § Results form basis of LDA and GGA approaches There have been few calculations of the EOS of inhomogeneous metals § Li†, Al* – VMC †(G. Yao, et. al. , Phys. Rev. B 54, 8393 (1996)), * (R. Gaudoin, et. al. , J. Phys. : Condens. Matter 14, 8787 (2002)) § Mg – DMC (M. Pozzo and D. Alfé, Phys. Rev. B 77, 104103 (2008)) Physical Sciences 29

Challenges for DMC - inhomogeneous metals Numerous semiconductors and insulators have been studied using QMC over the past 20 years § Inhomogeneous metals have a Fermi surface requiring larger supercells containing more electrons § Partial occupation of orbitals at Fermi level cannot be directly translated into a real used in DMC. Have an “open shell” which breaks symmetries Physical Sciences 30

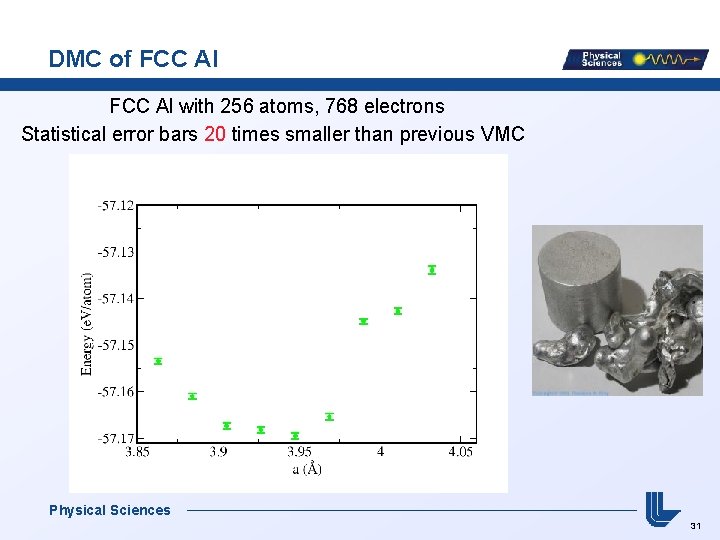
DMC of FCC Al with 256 atoms, 768 electrons Statistical error bars 20 times smaller than previous VMC Physical Sciences 31

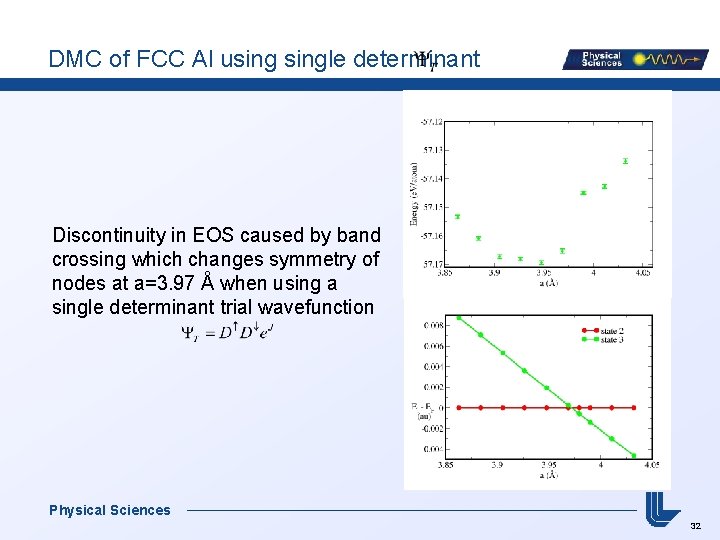
DMC of FCC Al usingle determinant Discontinuity in EOS caused by band crossing which changes symmetry of nodes at a=3. 97 Å when using a single determinant trial wavefunction Physical Sciences 32

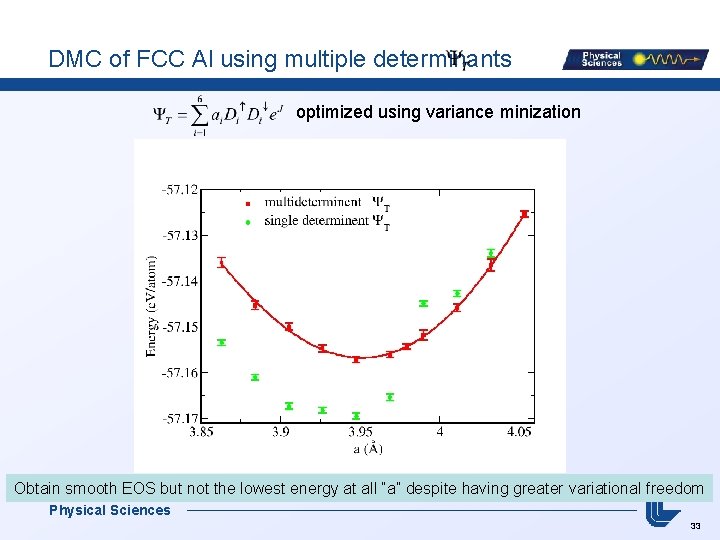
DMC of FCC Al using multiple determinants optimized using variance minization Obtain smooth EOS but not the lowest energy at all “a” despite having greater variational freedom Physical Sciences 33

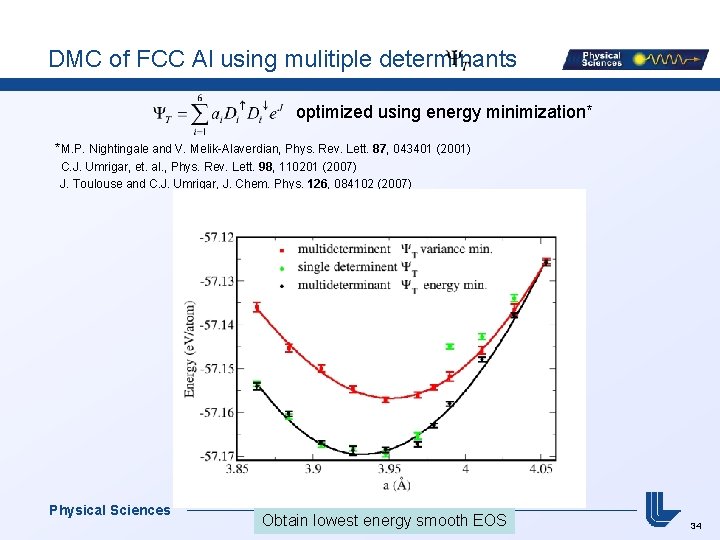
DMC of FCC Al using mulitiple determinants optimized using energy minimization* *M. P. Nightingale and V. Melik-Alaverdian, Phys. Rev. Lett. 87, 043401 (2001) C. J. Umrigar, et. al. , Phys. Rev. Lett. 98, 110201 (2007) J. Toulouse and C. J. Umrigar, J. Chem. Phys. 126, 084102 (2007) Physical Sciences Obtain lowest energy smooth EOS 34

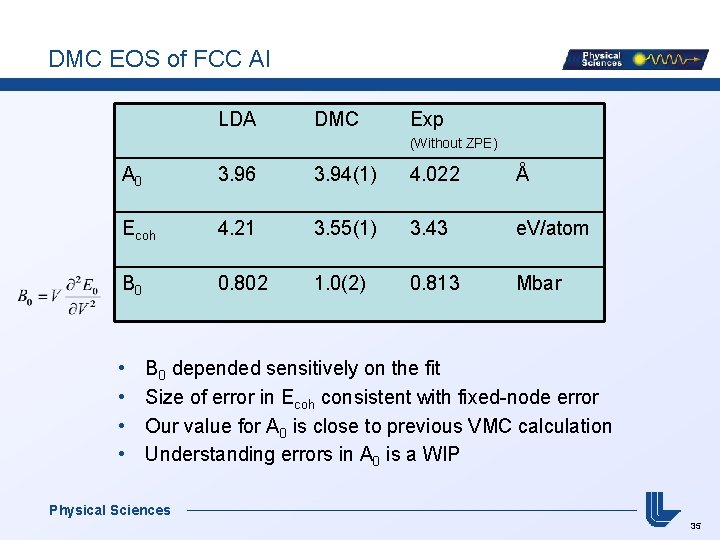
DMC EOS of FCC Al LDA DMC Exp (Without ZPE) A 0 3. 96 3. 94(1) 4. 022 Å Ecoh 4. 21 3. 55(1) 3. 43 e. V/atom B 0 0. 802 1. 0(2) 0. 813 Mbar • • B 0 depended sensitively on the fit Size of error in Ecoh consistent with fixed-node error Our value for A 0 is close to previous VMC calculation Understanding errors in A 0 is a WIP Physical Sciences 35

Conclusions • DMC is only feasible approach capable of directly treating the weak dispersive interaction for systems with more than a few atoms • DMC calculated EOS of FCC argon agrees closely with experiment, while DFT fails • Van der Waals interactions play a key role in H 2 absorption in planer hydrocarbon absorbents • Computed EOS of FCC aluminum Physical Sciences 36

Acknowledgments Jonathan Dubois Norm Tubman Sebastien Hamel Eric Schwegler (LLNL) (Northwestern) (LLNL) Shengbai Zhang Yiyang Sun Yong Hyun Kim (RPI) (NREL) Physical Sciences 37

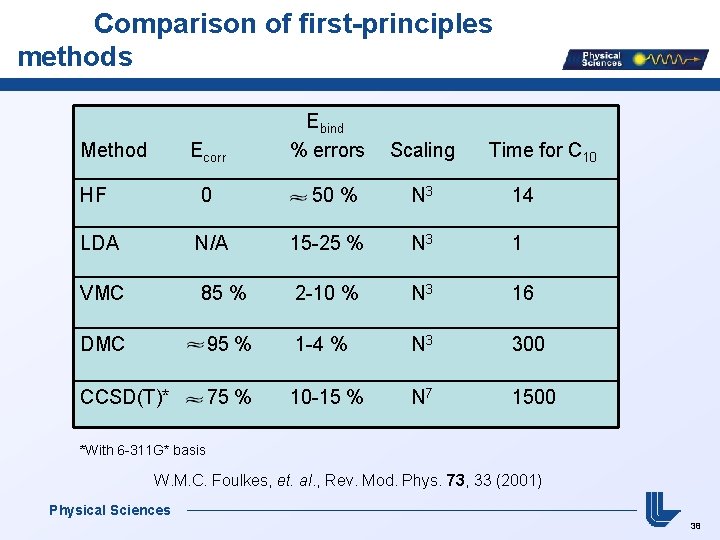
Comparison of first-principles methods Method Ecorr HF 0 LDA N/A VMC Ebind % errors 50 % Scaling Time for C 10 N 3 14 15 -25 % N 3 1 85 % 2 -10 % N 3 16 DMC 95 % 1 -4 % N 3 300 CCSD(T)* 75 % 10 -15 % N 7 1500 *With 6 -311 G* basis W. M. C. Foulkes, et. al. , Rev. Mod. Phys. 73, 33 (2001) Physical Sciences 38