Performance Evaluation of DPSK Optical Fiber Communication Systems

Performance Evaluation of DPSK Optical Fiber Communication Systems DPSK: Differential Phase-Shift Keying, a modulation technique that codes information by using the phase difference between two neighboring symbols. Jin Wang April 22, 2004

Outline 1. 2. 3. 4. 5. Introduction Bit Error Analysis in DPSK Systems Transmission Impairments in DPSK Systems Electrical Equalizer in DPSK Systems Nonlinear DPSK Systems 2

1. Introduction 3

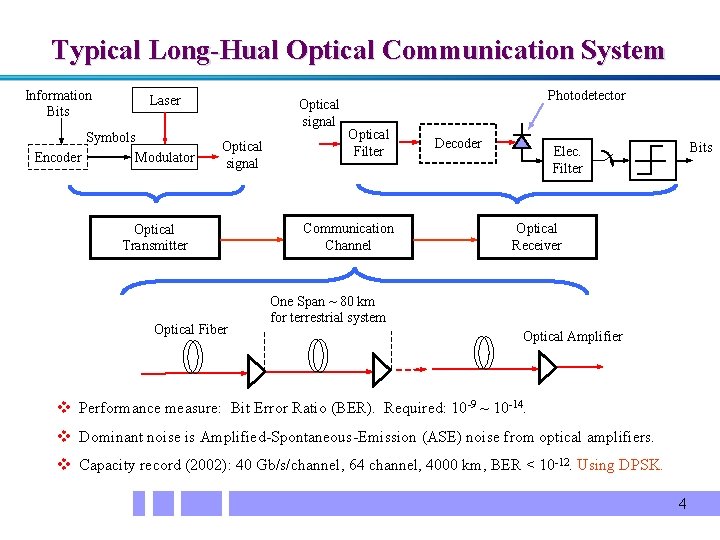
Typical Long-Hual Optical Communication System Information Bits Laser Symbols Encoder Modulator Optical signal Optical Transmitter Optical Fiber Photodetector Optical Filter Communication Channel Decoder Bits Elec. Filter Optical Receiver One Span ~ 80 km for terrestrial system Optical Amplifier v Performance measure: Bit Error Ratio (BER). Required: 10 -9 ~ 10 -14. v Dominant noise is Amplified-Spontaneous-Emission (ASE) noise from optical amplifiers. v Capacity record (2002): 40 Gb/s/channel, 64 channel, 4000 km, BER < 10 -12. Using DPSK. 4

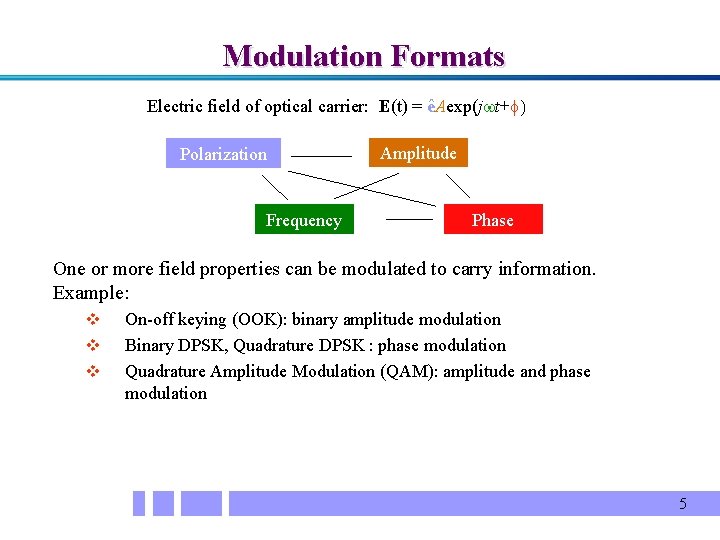
Modulation Formats Electric field of optical carrier: E(t) = êAexp(jwt+f) Polarization Frequency Amplitude Phase One or more field properties can be modulated to carry information. Example: v v v On-off keying (OOK): binary amplitude modulation Binary DPSK, Quadrature DPSK : phase modulation Quadrature Amplitude Modulation (QAM): amplitude and phase modulation 5

DPSK in Optical Systems 1. Early Experiments ( ~ 1990) v v 2. For the improvement of receiver sensitivity (At BER 10 -9, 1000 photons/bit for OOK v. s. < 100 photons/bit for DPSK) Low bit rate: ~ 1 Gb/s Cooling ( 90’s ) After the Advent of Optical Amplifiers v v v 3. High sensitivity OOK receiver (<100 photons/bit) can be realized with the aid of optical amplifier (Ex. Erbium-Doped Fiber Amplifier) Complicated DPSK transmitter and receiver Stringent requirements on laser linewidth (< 1% of data rate) Recent Revival ( ~ 2002) v v v For the improvement of receiver sensitivity (< 50 photons/bit), reduction of fiber nonlinearity and increase of spectrum efficiency Interferometric demodulation + direct detection Data rates of 10 Gb/s and 40 Gb/s relaxed linewidth requirements 6

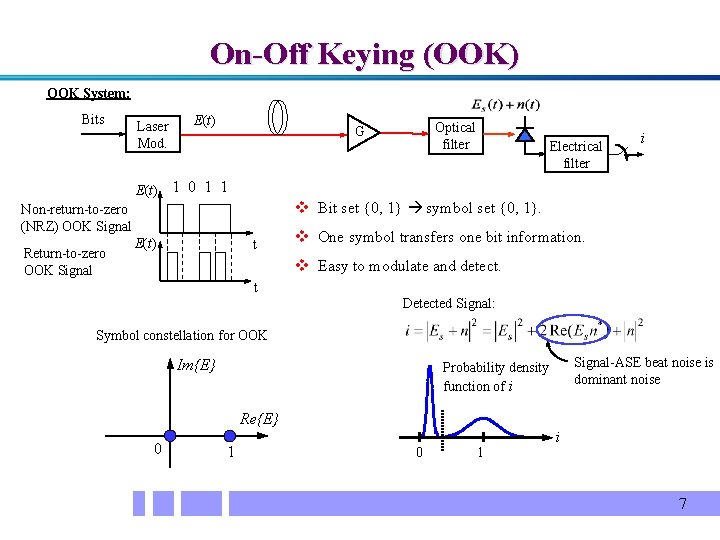
On-Off Keying (OOK) OOK System: Bits Laser Mod. E(t) Electrical filter i 1 0 1 1 v Bit set {0, 1} symbol set {0, 1}. Non-return-to-zero (NRZ) OOK Signal Return-to-zero OOK Signal Optical filter G E(t) t v One symbol transfers one bit information. v Easy to modulate and detect. t Detected Signal: Symbol constellation for OOK Im{E} Signal-ASE beat noise is dominant noise Probability density function of i Re{E} 0 1 i 7

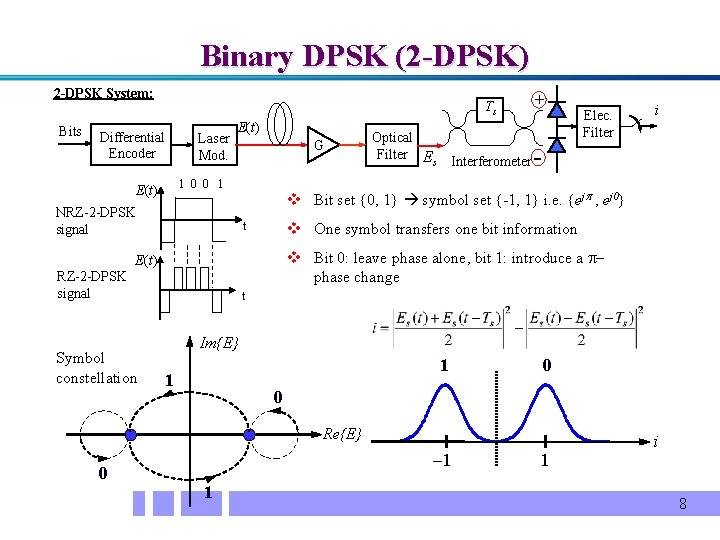
Binary DPSK (2 -DPSK) 2 -DPSK System: Bits Ts Differential Encoder Laser Mod. E(t) G 1 0 0 1 E(t) NRZ-2 -DPSK signal Optical Filter E Interferometer s i v One symbol transfers one bit information t v Bit 0: leave phase alone, bit 1: introduce a p phase change RZ-2 -DPSK signal t Im{E} 1 1 0 0 Re{E} 0 Elec. Filter v Bit set {0, 1} symbol set {-1, 1} i. e. {ej , ej 0} E(t) Symbol constellation + 1 1 1 i 8

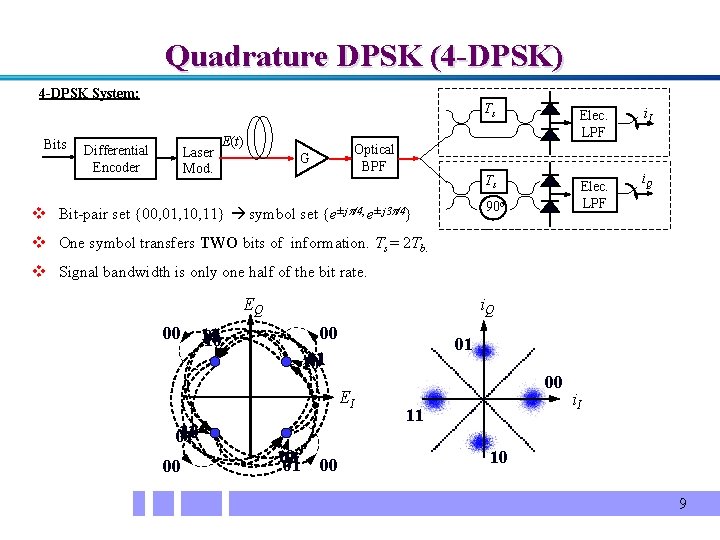
Quadrature DPSK (4 -DPSK) 4 -DPSK System: Bits Differential Encoder Laser Mod. E(t) Optical BPF G Ts Elec. LPF 90 o v Bit-pair set {00, 01, 10, 11} symbol set {e± j /4, e± j 3 /4} i. I i. Q v One symbol transfers TWO bits of information. Ts = 2 Tb. v Signal bandwidth is only one half of the bit rate. EQ 00 i. Q 00 11 01 10 01 EI 11 10 01 00 10 11 01 00 00 11 i. I 10 9

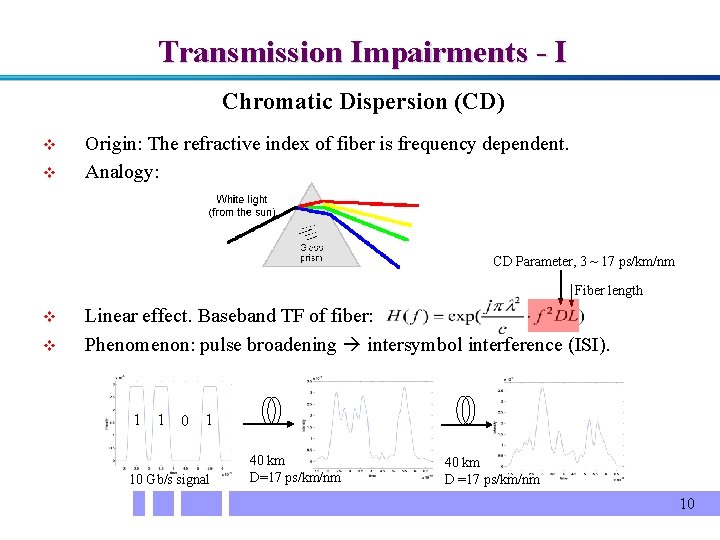
Transmission Impairments - I Chromatic Dispersion (CD) v v Origin: The refractive index of fiber is frequency dependent. Analogy: CD Parameter, 3 ~ 17 ps/km/nm Fiber length v v Linear effect. Baseband TF of fiber: Phenomenon: pulse broadening intersymbol interference (ISI). 1 1 0 1 10 Gb/s signal 40 km D=17 ps/km/nm 40 km D =17 ps/km/nm 10

Transmission Impairments - II Fiber Nonlinearity (FNL) v v Origin: The refractive index of fiber is power dependent. Nonlinear Schrödinger equation (wave equation in fiber): CD v FNL Effects: § § § v Fiber Loss No analytic solutions for general input, numerical approach necessary (split-step FFT) Self-phase modulation (SPM) spectrum broadening. Cross-phase modulation (XPM) spectrum broadening. Four-wave mixing (FWM) noise amplification. interchannel crosstalk. Spectrum broadening + CD intersymbol interference. 11

Transmission Impairments - III Polarization Mode Dispersion (PMD) v Origin: fast axis ideal fiber v real fiber slow axis Principal states model Input field E 0(t) : power splitting ratio. : differential group delay. v Linear effect in optical domain. Baseband TF of fiber with PMD: v PMD stochastic. PMD causes ISI. Impact . 12

Challenges for Optical Communication Systems Challenges Solutions Transmission at ultra high bit rate requires extremely low CD. Reduce signal bandwidth by transmitting multibits with one symbol. (4 -DPSK) Long transmission distance causes significant FNL. Reduce FNL by decreasing signal power and its variation. (2 -DPSK and 4 -DPSK) Ultra short bit period implies high sensitivity to PMD. Increase symbol period transmitting multi-bits with one symbol. (4 -DPSK) Fixed channel bandwidth, increasing bit rate. Improve spectrum efficiency by transmitting multi-bits with one symbol. (4 -DPSK) 13

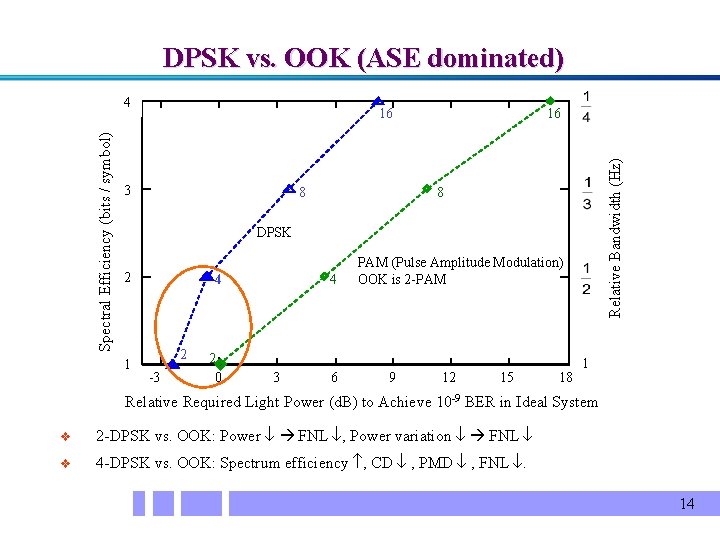
DPSK vs. OOK (ASE dominated) 16 3 8 16 Relative Bandwidth (Hz) Spectral Efficiency (bits / symbol) 4 8 DPSK 2 1 4 2 -3 2 0 4 3 6 PAM (Pulse Amplitude Modulation) OOK is 2 -PAM 9 12 15 18 1 Relative Required Light Power (d. B) to Achieve 10 -9 BER in Ideal System v 2 -DPSK vs. OOK: Power FNL , Power variation FNL v 4 -DPSK vs. OOK: Spectrum efficiency , CD , PMD , FNL . 14

How Robust is DPSK? CD PMD Impacts on DPSK not quantified before. FNL Reasons for the dearth of impact analysis: v The BER of DPSK systems has been difficult to calculate, because of the squaring effect of photodetector. v The interaction of CD and FNL in fiber increases the difficulty of modeling optical noise in fiber. 15

2. Bit Error Analysis in DPSK Systems 16

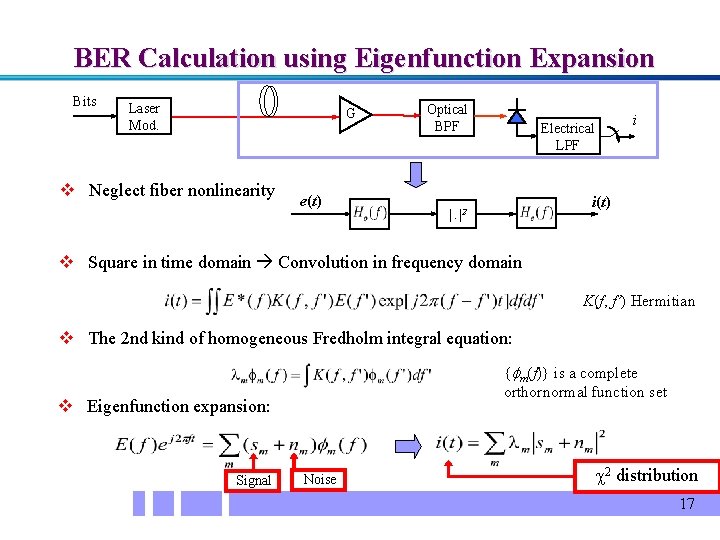
BER Calculation using Eigenfunction Expansion Bits Laser Mod. G v Neglect fiber nonlinearity e(t) Optical BPF i Electrical LPF i(t) |. |2 v Square in time domain Convolution in frequency domain K(f, f’) Hermitian v The 2 nd kind of homogeneous Fredholm integral equation: { m(f)} is a complete orthornormal function set v Eigenfunction expansion: Signal Noise 2 distribution 17

BER calculation in DPSK system – II One more step to obtain BER: Moment generating function (MGF) of i(t) is (s), i. e. , (s)= E[esi] = Laplace transform of PDF of i(t) L-1 PDF of i(t) di BER (CDF of i(t)) One Integral We use saddle point integration method to calculate the integral of MGF. 18

Saddle Point Integration v Also called stationary phase method, especially in physics. v Basic idea: For the calculation of line integral : If amplitude f(u) changes slowly compared to phase q(u), the main contribution to the integral comes from very near u 0 where the phase is stationary, i. e, q(u) u u 0 19

Accuracy of BER calculation method v 10 Gb/s system, with Gaussian optical filter and 5 th-order Bessel electrical filter. 4 -DPSK 2 -DPSK OSNR is optical signal-to-noise ratio 20

3. Transmission Impairments in DPSK Systems 21

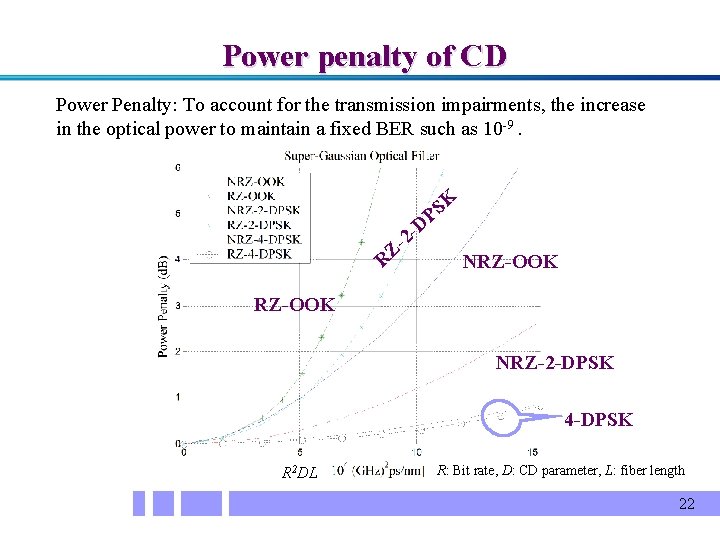
Power penalty of CD Power Penalty: To account for the transmission impairments, the increase in the optical power to maintain a fixed BER such as 10 -9. K S P D - -2 Z R NRZ-OOK NRZ-2 -DPSK 4 -DPSK R 2 DL CDrate, parameter, Bit rate, L: fiber length R: D: Bit D: CDR: parameter, L: fiber length 22

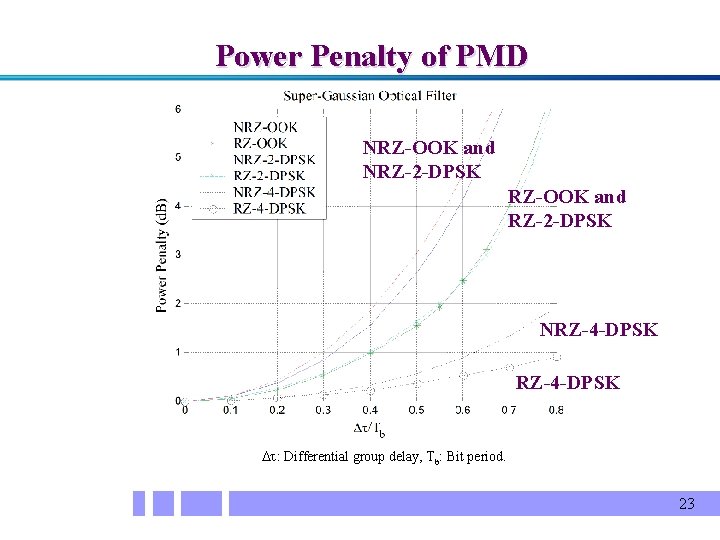
Power Penalty of PMD NRZ-OOK and NRZ-2 -DPSK RZ-OOK and RZ-2 -DPSK NRZ-4 -DPSK : Differential group delay, Tb: Bit period. 23

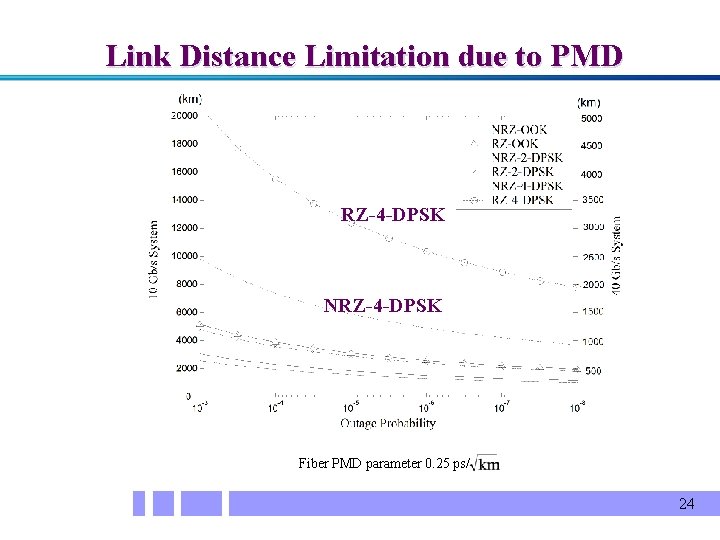
Link Distance Limitation due to PMD RZ-4 -DPSK NRZ-4 -DPSK Fiber PMD parameter 0. 25 ps/ 24

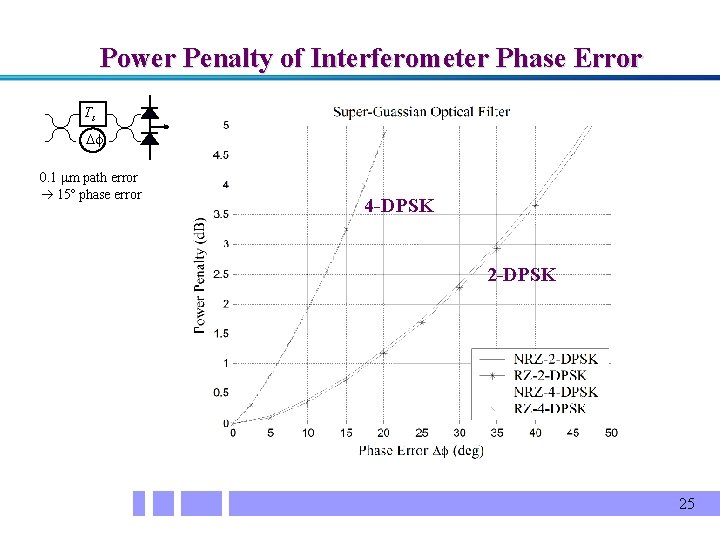
Power Penalty of Interferometer Phase Error Ts f 0. 1 mm path error 15º phase error 4 -DPSK 25

4. Electrical Equalizer in DPSK Systems 26

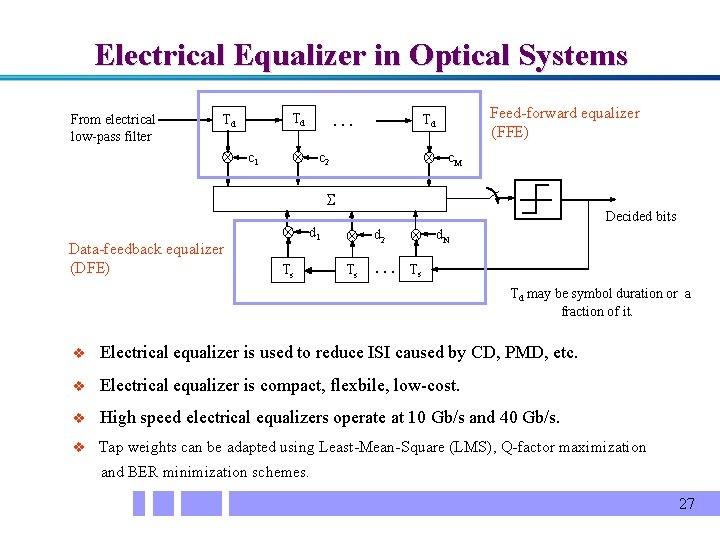
Electrical Equalizer in Optical Systems From electrical low-pass filter … Td Td c 1 Feed-forward equalizer (FFE) Td c 2 c. M Decided bits Data-feedback equalizer (DFE) d 1 Ts d 2 Ts … d. N Ts Td may be symbol duration or a fraction of it. v Electrical equalizer is used to reduce ISI caused by CD, PMD, etc. v Electrical equalizer is compact, flexbile, low-cost. v High speed electrical equalizers operate at 10 Gb/s and 40 Gb/s. v Tap weights can be adapted using Least-Mean-Square (LMS), Q-factor maximization and BER minimization schemes. 27

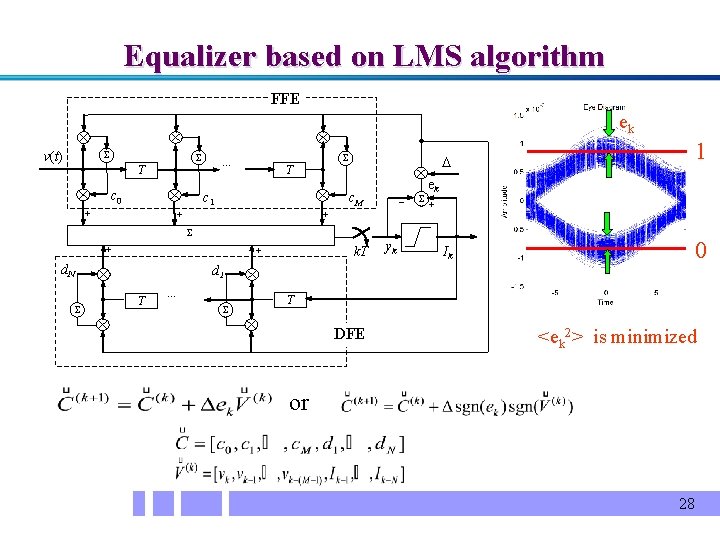
Equalizer based on LMS algorithm FFE ek v(t) … T c 0 T c 1 + c. M + _ + 1 Ik 0 ek + + k. T + d. N d 1 T … yk T DFE <ek 2> is minimized or 28

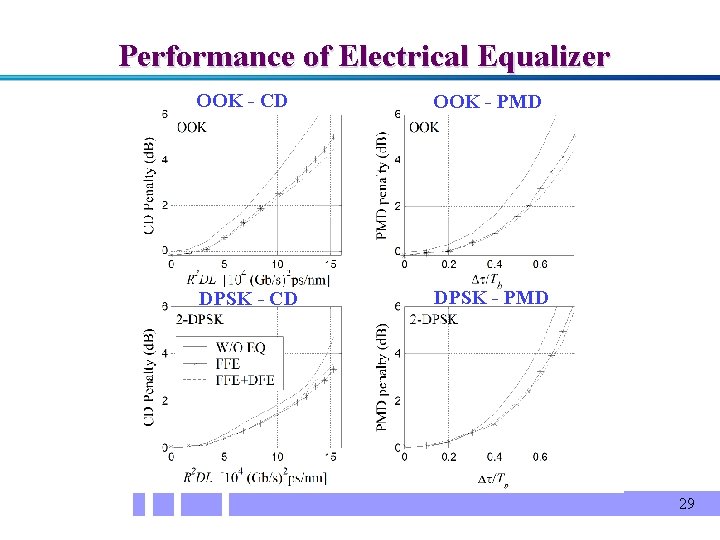
Performance of Electrical Equalizer OOK - CD OOK - PMD DPSK - CD DPSK - PMD 29

5. Nonlinear DPSK Systems 30

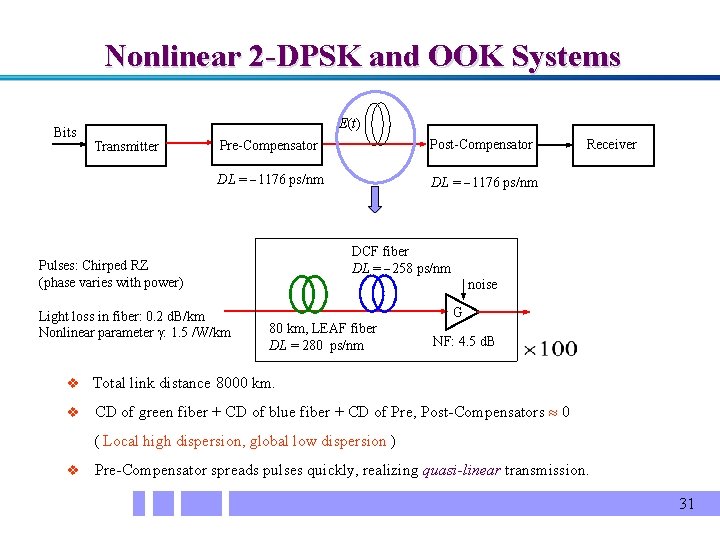
Nonlinear 2 -DPSK and OOK Systems Bits E(t) Transmitter Pre-Compensator Post-Compensator DL = 1176 ps/nm DCF fiber DL = 258 ps/nm Pulses: Chirped RZ (phase varies with power) Light loss in fiber: 0. 2 d. B/km Nonlinear parameter : 1. 5 /W/km Receiver noise G 80 km, LEAF fiber DL = 280 ps/nm NF: 4. 5 d. B v Total link distance 8000 km. v CD of green fiber + CD of blue fiber + CD of Pre, Post-Compensators 0 ( Local high dispersion, global low dispersion ) v Pre-Compensator spreads pulses quickly, realizing quasi-linear transmission. 31

BER Calculation in Nonlinear DPSK System v No noise model for general nonlinear DPSK or OOK system. v No BER calculation method for general nonlinear DPSK or OOK system. v Q-factor is not a reliable performance measure, especially for DPSK system (2~3 d. B OSNR error). v In CRZ-DPSK or CRZ-OOK system, noise can be modeled as additive non-white Gaussian noise because of low fiber nonlinearity. v Non-white Gaussian noise model + eigenfunction expansion method yields accurate BER. 32

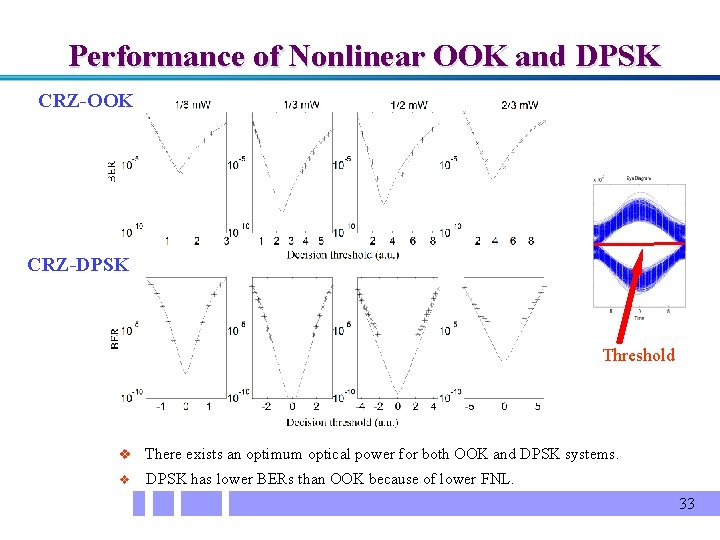
Performance of Nonlinear OOK and DPSK CRZ-OOK CRZ-DPSK Threshold v There exists an optimum optical power for both OOK and DPSK systems. v DPSK has lower BERs than OOK because of lower FNL. 33

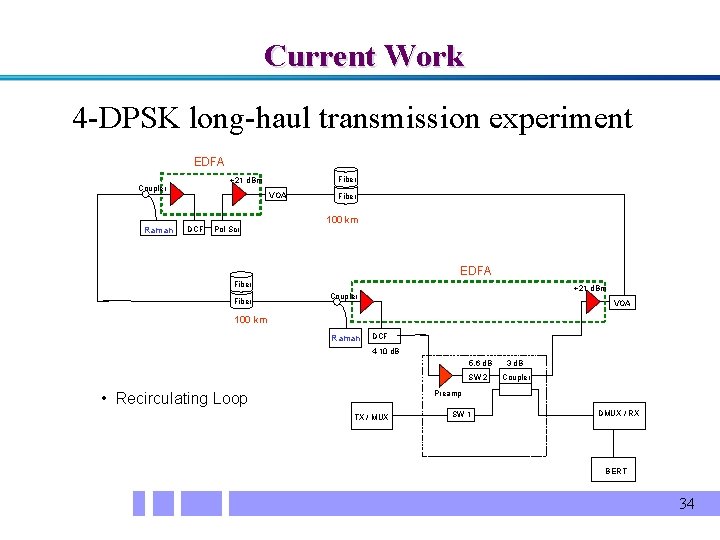
Current Work 4 -DPSK long-haul transmission experiment EDFA Raman Fiber +21 d. Bm Coupler VOA DCF Pol Scr Fiber 100 km EDFA Fiber +21 d. Bm Coupler VOA 100 km Raman DCF 4 -10 d. B 5. 6 d. B 3 d. B SW 2 Coupler Preamp • Recirculating Loop TX / MUX SW 1 DMUX / RX BERT 34