Performance Characterization of Vector and Array Processors 12292021

Performance Characterization of Vector and Array Processors 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 1

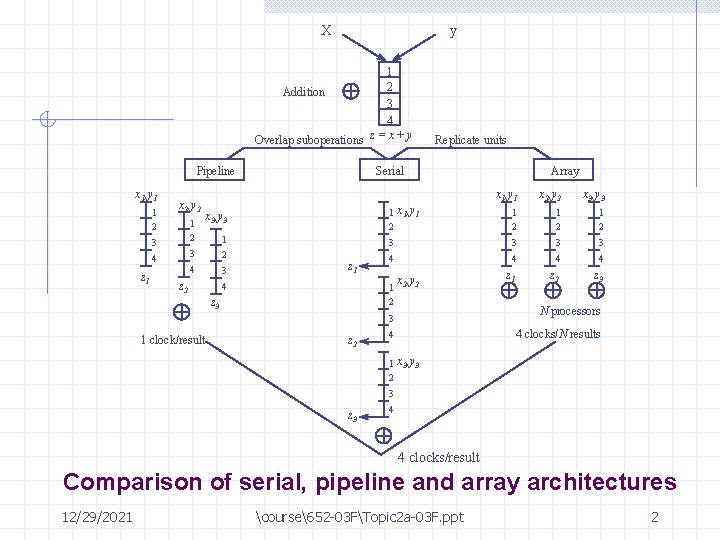
X y 1 2 Addition 3 4 z = x+ y Overlap suboperations Pipeline x 1, y 1 1 2 x 2, y 2 4 z 1 Serial x 1, y 1 Array x 1, y 1 x 2, y 2 x 3, y 3 1 2 1 2 x 3, y 3 1 2 3 3 4 4 4 3 z 1 z 2 z 3 1 2 3 Replicate units z 2 z 1 4 1 2 z 3 x 2, y 2 N processors 3 1 clock/result z 2 4 clocks/N results 4 1 2 x 3, y 3 3 z 3 4 4 clocks/result Comparison of serial, pipeline and array architectures 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 2

An Example Zi = Xi + Yi (i = 1. . . n) Assume l = # stages = time for each stage (usually is taken as the clock cycle) n = vector length 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 3

Generic Performance Formula (R. Hockney & C. Jesshope 81) t=r • r : -1( n+n 1/2 ) Maximum rate or asymptotic performance (infinite length vector) • n 1/2 : half-performance length, or the vector length required to achieve half of the maximum performance. 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 4

Example of Serial Computers generic t = r -1( n+n 1/2 ) t serial = l n r serial 12/29/2021 -1 serial n 1/2 =l =0 course652 -03 FTopic 2 a-03 F. ppt 5

Example of Pipelined Computers generic t pipe = [s + l + (n-1)] t pipe = r -1( n + n 1/2 ) = [n + (s + l - 1)] r -1 pipe n 1/2 = =s+l-1 pipe 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 6

So r -1 : a characteristic of the technology, a scale factor applied to the performance of a particular architecture implemented with a particular tech. when compare relative performance, it cancels out. n 1/2 : 12/29/2021 a measure of the amount of parallelism in the architecture course652 -03 FTopic 2 a-03 F. ppt 7

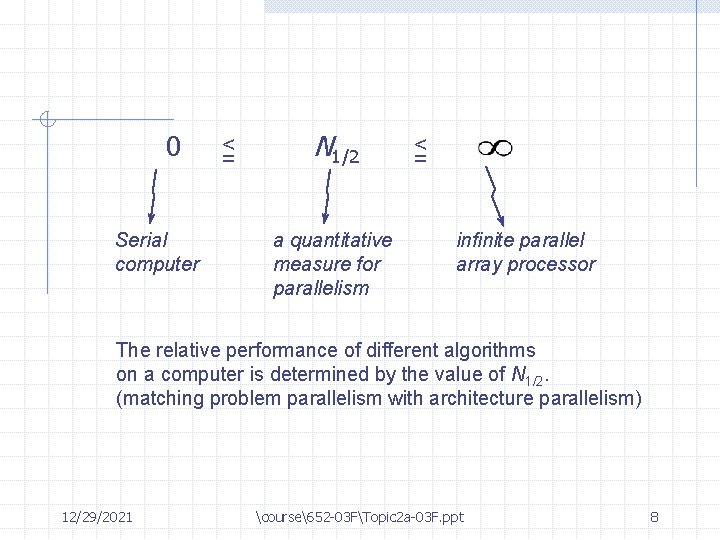
0 Serial computer < = N 1/2 a quantitative measure for parallelism < = infinite parallel array processor The relative performance of different algorithms on a computer is determined by the value of N 1/2. (matching problem parallelism with architecture parallelism) 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 8

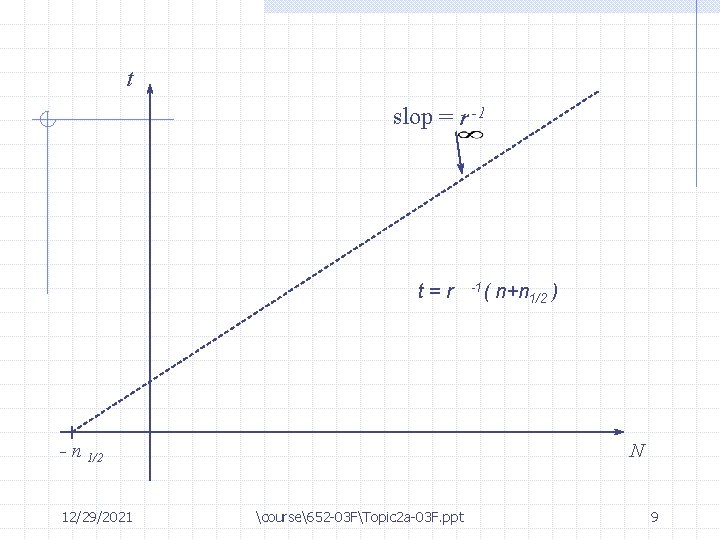
t slop = r -1 t=r - n 1/2 12/29/2021 -1( n+n 1/2 ) N course652 -03 FTopic 2 a-03 F. ppt 9

Measurement of n 1/2 and r Call Second (T 1 ) Call Second (T 2 ) T 0 = T 2 - T 1 Do 20 N = 1, NMAX Call Second (T 1 ) Do 10, I = 1, N 10 A(I) = B(I) * C(I) Call 20 12/29/2021 Second (T 2 ) T = T 2 - T 1 - T 0 course652 -03 FTopic 2 a-03 F. ppt 10

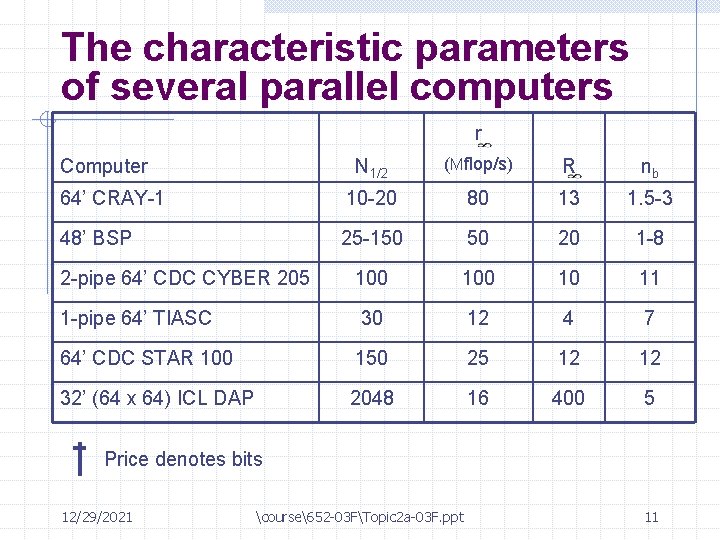
The characteristic parameters of several parallel computers r N 1/2 (Mflop/s) R nb 64’ CRAY-1 10 -20 80 13 1. 5 -3 48’ BSP 25 -150 50 20 1 -8 2 -pipe 64’ CDC CYBER 205 100 10 11 1 -pipe 64’ TIASC 30 12 4 7 64’ CDC STAR 100 150 25 12 12 32’ (64 x 64) ICL DAP 2048 16 400 5 Computer Price denotes bits 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 11

Examples of Performance Analysis 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 12

Chaining Effect Assume M vector operations • Unchained tm = = So So m i=1 m [si + li + (n-1)] [(si + li - 1) + n] i=1 t= 1 m tm m t= [ 1 (n 1/2)i + m i=1 n 1/2 = s + l - 1 1 mn] m (assume S 1 = S 2 =. . . r = 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt l 1 = l 2 =. . . ) 13

• for m chained vector ops tm = [ m (si + li ) + (n-1)] i=1 = [m since t = so so t = r -1 1 m m (s + l ) + (n-1)] tm [m (s + l ) + (n-1)] Can not move in [ ]. = m n 1/2 = m (s+l) - 1 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 14

Note: r chaining =m r (n 1/2)chaining = m n 1/2 This is understood if we compare “a chain of m pipe” with “an array of m PE” 12/29/2021 course652 -03 FTopic 2 a-03 F. ppt 15