Perfidious Polynomials and Elusive Roots Zhonggang Zeng Northeastern

Perfidious Polynomials and Elusive Roots Zhonggang Zeng Northeastern Illinois University Nov. 2, 2001 at Northern Illinois University

What are the “best” functions? 1. Linear functions 2. Polynomials 3. Exponential functions 4. Trigonometric functions. . . Weierstrass Theorem: Any continuous function can be approximated to any accuracy by a polynomial of sufficiently high degree. Why by a polynomial ?

Polynomial root-finding xn + a 1 xn-1 + a 2 xn-2 +. . . + an-1 x + a 0 = 0 has played a key role in the history of mathematics - Rational/irrational numbers, complex numbers - Fundamental Theorem of Algebra - Abel and Galois Theorem. . .

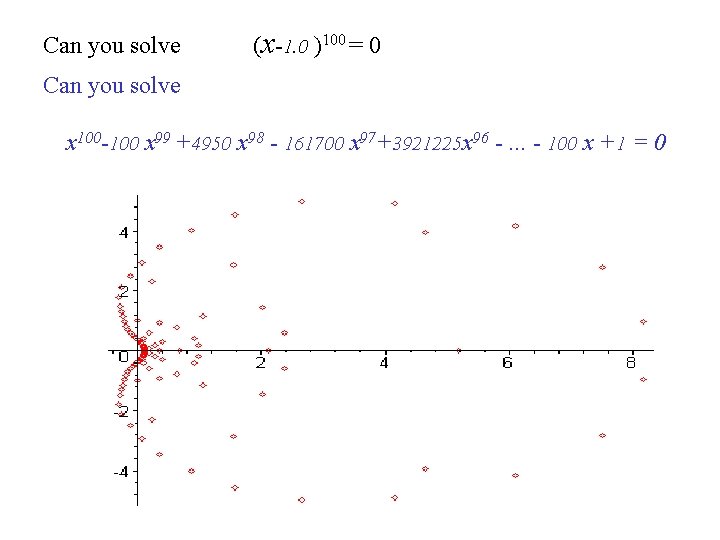
Can you solve (x-1. 0 )100 = 0 Can you solve x 100 -100 x 99 +4950 x 98 - 161700 x 97+3921225 x 96 -. . . - 100 x +1 = 0

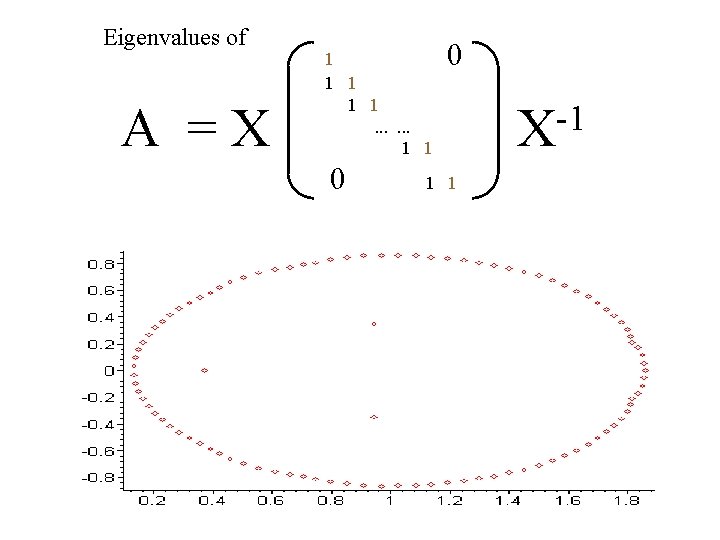
Eigenvalues of A =X 1 1 1. . . 1 1 0 0 1 1 -1 X

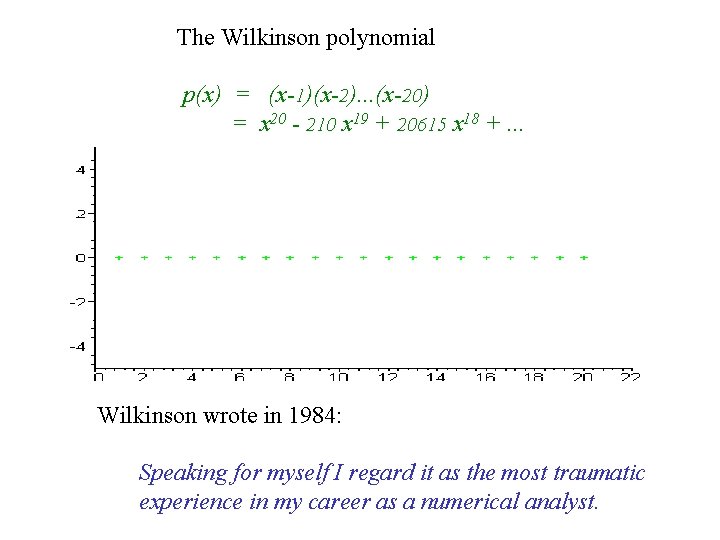
The Wilkinson polynomial p(x) = (x-1)(x-2). . . (x-20) = x 20 - 210 x 19 + 20615 x 18 +. . . Wilkinson wrote in 1984: Speaking for myself I regard it as the most traumatic experience in my career as a numerical analyst.

Classical textook methods for multiple roots Newton’s iteration xj+1 = xj - f(xj)/f’(xj), j=0, 1, 2, . . . converges locally to a multiple root of f(x) with a linear rate. The modified Newton’s iteration xj+1 = xj - mf(xj)/f’(xj), j=0, 1, 2, . . . converges locally to a m-fold root of f(x) with a quadratic rate. Newton’s iteration applied to g(x) = f(x)/f’(x) converges locally and quadratically to a root of f(x) regardliss of its multiplicity. None of them work!

Example: f(x) = (x-2)7(x-3)(x-4) in expanded form. Modified Newton’s iteration with m = 7 intended for root x = 2: x 1 = 1. 9981 x 2 = 1. 7481 x 3 = 1. 9892 x 4 = 0. 4726 x 5 = 1. 8029 x 6 = 1. 9931 x 7 = 4. 2681 x 8 = 3. 3476. . .

Myths on polynomial roots: - multiple roots are ill-conditioned, or even intractable - extension of machine precision is necessary to calculate multiple roots - there is an “attainable precision” for multiple roots: machine precision attainable precision = --------------multiplicity Example: for 100 -fold root, to get 5 digits right 500 digits in machine precision 5 digits precision = --------------------100 in multiplicity

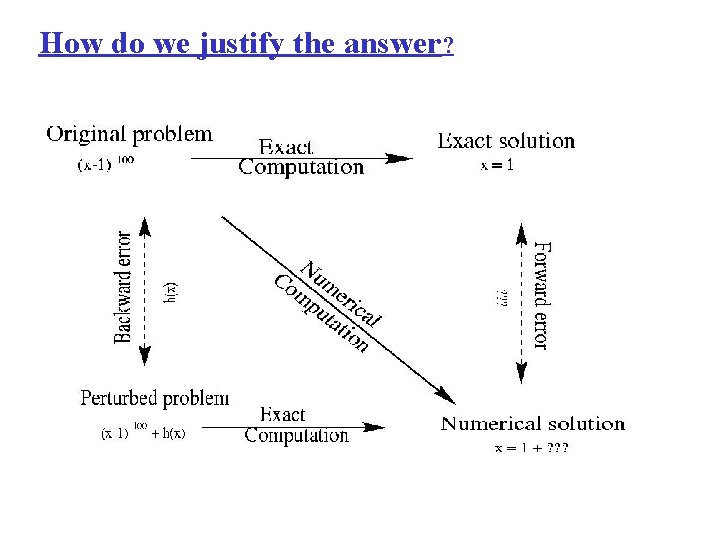
How do we justify the answer?

The condition number [Forward error] ~ [Condition number] [Backward error] From problem From computational method A large condition number <=> The problem is sensitive or, ill-conditioned

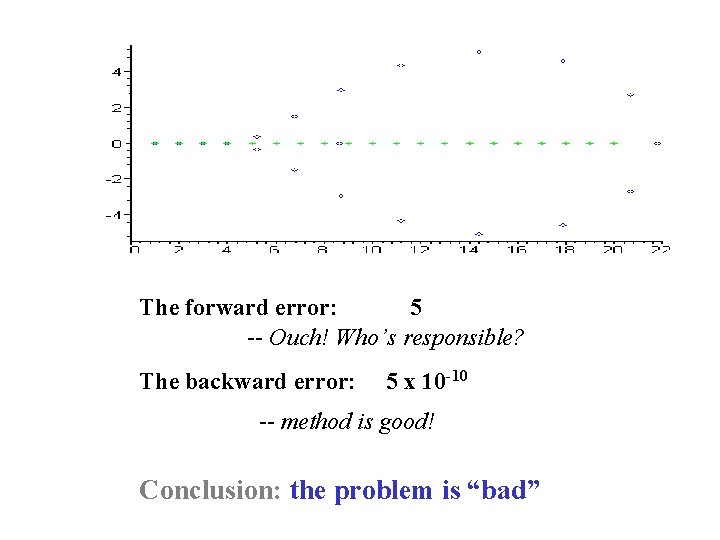
The forward error: 5 -- Ouch! Who’s responsible? The backward error: 5 x 10 -10 -- method is good! Conclusion: the problem is “bad”

If the answer is highly sensitive to perturbations, you have probably asked the wrong question. Maxims about numerical mathematics, computers, science and life, L. N. Trefethen. SIAM News Who is asking a wrong question? A: “Customer” B: Numerical analyst What is the wrong question? A: The polynomial B: The computing objective

The question we used to ask: ask (Fundamental Theorem of Algebra) Given a polynomial p(x) = xn + a 1 xn-1+. . . +an-1 x + an find z = ( z 1, . . . , zn ) such that p(x) = ( x - z 1 )( x - z 2 ). . . ( x - zn ) Right - or - Wrong ?

Kahan’s pejorative manifolds All n-polynomials having certain multiplicity structure form a pejorative manifold xn + a 1 xn-1+. . . +an-1 x + an <=> (a 1 , . . . , an-1 , an ) Example: ( x-t )2 = x 2 + (-2 t) x + t 2 Pejorative manifold: a 1= -2 t a 2= t 2

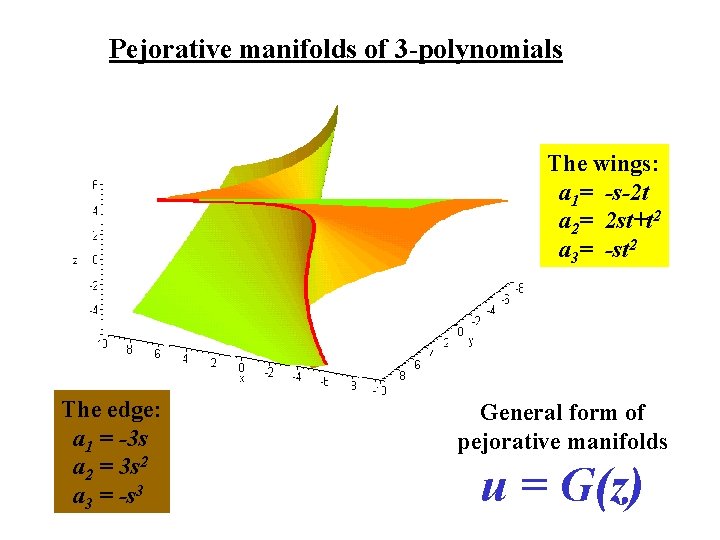
Pejorative manifolds of 3 -polynomials ( x - s )( x - t )2 = x 3 + (-s-2 t) x 2 + (2 st+t 2) x + (-st 2) Pejorative manifold of multiplicity structure [1, 2] a 1= -s-2 t a 2= 2 st+t 2 a 3= -st 2 ( x - s )3 = x 3 + (-3 s) x 2 + (3 s 2) x + (-s 3) Pejorative manifold of multiplicity structure [ 3 ] a 1 = -3 s a 2 = 3 s 2 a 3 = -s 3

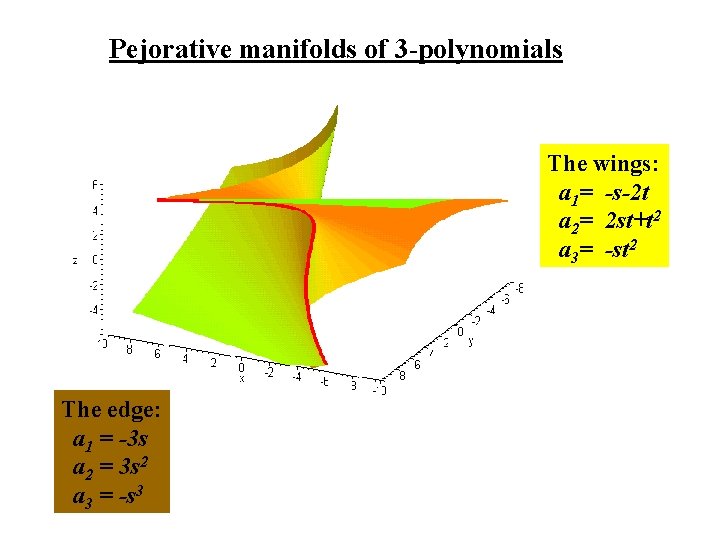
Pejorative manifolds of 3 -polynomials The wings: a 1= -s-2 t a 2= 2 st+t 2 a 3= -st 2 The edge: a 1 = -3 s a 2 = 3 s 2 a 3 = -s 3 General form of pejorative manifolds u = G(z)

W. Kahan, Conserving confluence curbs ill-condition, 1972 1. Ill-condition occurs when a polynomial is near a pejorative manifold. 2. A small “drift” by a polynomial on that pejorative manifold does not cause large forward error to the multiple roots, except 3. If a multiple root is sensitive to small perturbation on the pejorative manifold, then the polynomial is near a pejorative submanifold of higher multiplicity. Ill-condition is caused by solving polynomial equations on a wrong manifold

Pejorative manifolds of 3 -polynomials The wings: a 1= -s-2 t a 2= 2 st+t 2 a 3= -st 2 The edge: a 1 = -3 s a 2 = 3 s 2 a 3 = -s 3

Given a polynomial p(x) = xn + a 1 xn-1+. . . +an-1 x + an The wrong question: /Find / / / (/ z/1, /. . . , / z/n )/ such / / / that / / /p(x) / / =/ (/ x/ - /z 1/)(/ x/ - /z 2/) /. . . /( /x -/ z/n )/ because you are asking for simple roots! The right question: Find distinct z 1, . . . , zm such that p(x) = ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm s 1+. . . + sm = n, m < n do it on the pejorative manifold!

For ill-conditioned polynomial p(x)= xn + a 1 xn-1+. . . +an-1 x + an ~ a = (a 1 , . . . , an-1 , an ) The objective: find u*=G(z*) that is nearest to p(x)~a

( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm = Let xn + g 1 ( z 1, . . . , zm ) xn-1+. . . +gn-1 ( z 1, . . . , zm ) x + gn ( z 1, . . . , zm ) Then, p(x) = ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm n g 1 ( z 1, . . . , zm ) =a 1 g 2( z 1, . . . , zm ) =a 2. . gn ( z 1, . . . , zm ) =an (m<n) m I. e. An over determined polynomial system G(z) = a <==>

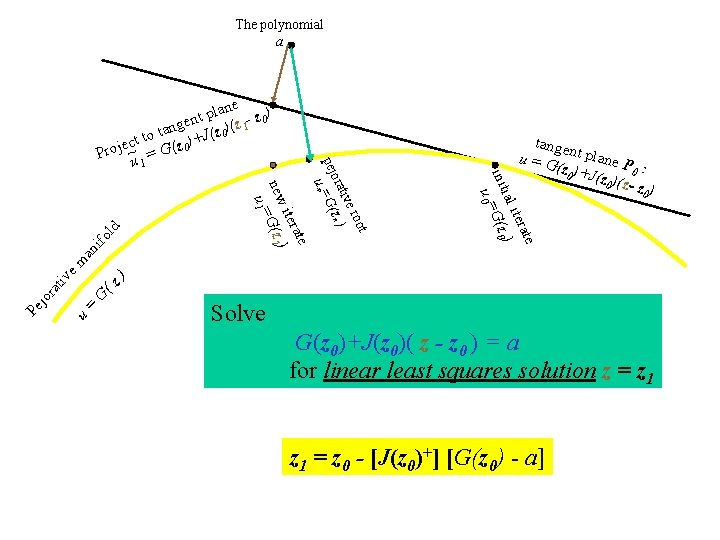
The polynomial a ld 0 (z ) ifo em an tiv u = G ra jo Pe t roo tive ora G(z * ) u *= ate iter ) new G(z 1 u 1= tange u = G nt plane P (z 0 )+J : (z 0 )(z 0 -z ) ate iter ) ial init G(z 0 u 0= pej lane z 0) p t ngen (z 0)(z 1 a t ct to (z 0)+J e j o Pr ~u = G 1 Solve G(z 0)+J(z G( z 0)() = z -az 0 ) = a for nonlinear for linearleastsquaressolutionz=z z =*z 1 G(z - z 0 0)))=-- aa] a] J(z -[J(z z 0 ) 00=))(+-]z[G(z z 1 = 0)( z 0 z 0 -)+J(z [G(z 0

zi+1=zi - J(zi )+[ G(zi )-a ], i=0, 1, 2. . . Theorem: If z=(z 1, . . . , zm) with z 1, . . . , zm distinct, then the Jacobian J(z) of G(z) is of full rank. Theorem: Let u*=G(z*) be nearest to p(x)~a, if 1. z*=(z*1, . . . , z*m) with z*1, . . . , z*m distinct; 2. z 0 is sufficiently close to z*; 3. a is sufficiently close to u* then the iteration converges with a linear rate. Further assume that a = u* , then the convergence is quadratic.

Calculation of G(z) and J(z) ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm = xn + g 1 ( z 1, . . . , zm ) xn-1+. . . +gn-1 ( z 1, . . . , zm ) x + gn ( z 1, . . . , zm ) Explicit polynomail formula gj ( z 1, . . . , zm ) is neither necessary nor desirable. G(z) and every column of J(z) are calculated via simple numerical procedures, as key components of the algorithm.

The conventional condition number Let f(x*) = 0 f(x(e)) + e g(x(e)) =0, x(0) = x* ----f’(x----(e)) x’(e) + g(x (e)) +/ e/ g’(x / / / (e)) / /x’/ (e) / / =0 x* x* x’(0) = - g(x*)/ f’(x*) x(e) = x* - e g(x*)/ f’(x*) + h. o. t. | x(e) - x | < | 1 / f’(x ) |. | e g(x ) | + h. o. t. * Condition number * * | 1 / f’(x ) | = infinity * at multiple a root

The “pejorative” condition number u= v= G( y) G( z) || u - v ||2 = backward error || y - z ||2 = forward error u - v = G(y) - G(z) = J(z) (y - z) + h. o. t. || u - v ||2 = || J(z) (y - z) ||2 > s || y - z ||2 < (1/s) || u - v ||2 1/s is the pejorative condition number where s is the smallest singular value of J(z).

Example 1 (x-1. 0 )100 = 0 To make the problem interesting: round the coefficients to 5 digits Step. . . 43 44 45 46 47 iterates. . 1. 007 1. 001 1. 0000003. 99998 conventional condition: pejorative condition: infinity 0. 0017 Is it ill-conditioned?

Example 2 (x-0. 9)18(x-1. 0)10(x-1. 1)16 = 0 Step z 1 z 2 z 3 ----------------------------------0. 92. 95 1. 12 1. 87 1. 05 1. 10 2. 95 1. 11 3. 88 1. 01 1. 10 4. 90. 97 1. 12 5. 901. 992 1. 101 6. 89993. 9998 1. 1002 7. 9000003. 999998 1. 1000007 8. 8999997. 9999991 1. 1000009 9. 900000006. 99999997 1. 10000001 forward error: backward error: 6 x 10 -15 8 x 10 -16 Pejorative condition: 58 Even clustered multiple roots are pejoratively well conditioned

If you are on a wrong manifold. . . Multiplicity pejorative roots backward error pejorative condition structure ------------------------------------------------------[1, 1, . . . 1] erratic. 000000006 1390704851032436. [18, 10, 16] (. 9000, 1. 0000, 1. 1000). 000000008 58. 2 [17, 11, 16] (. 8980, . 9934, 1. 1006). 0000005 51. 9 [14, 16, 14] (. 8890, . 9892, 1. 1090). 000006 29. 0 [10, 24, 10] (. 8711, . 9906, 1. 1316). 00001 25. 8 [ 2, 40, 2] (. 7393, . 9917, 1. 3282). 0001 23. 6 [ 1, 43] (. 6559, 1. 0053 ). 004 12. 9 [44] (. 9925 ). 04. 0058

Example 3 (x-. 3 -. 6 i)100 (x-. 1 -. 7 i) 200 (x -. 7 -. 5 i) 300 (x-. 3 -. 4 i) 400 =0 Scary enough? Z 1 . 289 +. 601 i. 309 +. 602 i. 293 +. 596 i. 300005 +. 600006 i. 3000002+. 60000005 i Round coefficients to 6 digits. z 2 . 100 +. 702 i. 097 +. 698 i. 101 +. 7003 i. 099998 +. 6999992 i. 09999995+. 69999998 i z 3 . 702 +. 498 i. 698 +. 499 i. 7002 +. 5005 i. 69999992+. 4999993 i. 69999997+. 49999998 i . 301 +. 399 i. 299 +. 401 i. 3007 +. 4003 i. 2999992 +. 3999992 i. 29999997+. 400000002 i Roots are correct up to 7 digits! Pejorative condition: 0. 58 z 4

Example 4: The Wilkinson polynomial p(x) = (x-1)(x-2). . . (x-20) = x 20 - 210 x 19 + 20615 x 18 +. . . There are 605 manifolds in total. It is near some manifolds, but which ones? Multiplicity backward error condition Estimated structure number error ------------------------------------[1, 1, 1. . . , 1]. 00000003 550195997640164 1. 6 [1, 1, 2, 2, 2, 4, 2, 2, 2]. 00003 29269411. 09 [1, 1, 1, 2, 3, 4, 5, 3]. 0000001 33563. 003 [1, 1, 2, 3, 4, 6, 3]. 000001 6546. 007 [1, 1, 2, 5, 7, 4]. 000005 812. 004 [1, 2, 5, 7, 5]. 00004 198. 008 [1, 3, 8, 8]. 0002 25. 005 [2, 8, 10]. 003 6. 02 [5, 15]. 04 1. 04 [20]. 9. 2. 2 What are the roots of the Wilkinson polynomial? Choose your poison!

If the estimated error is the sole criterion. . . Roots multiplicity --------------. 9999012 * 2. 0012667 * 2. 9758883 * 4. 3848008 ** 6. 9548807 *** 10. 3585762 **** 15. 0276741 ***** 19. 2719863 *** The polynomial with these roots matches W. Polynomial for 6 digits The condition 33563 is manageable.

Summary of the simultaneous method: - Given a polynomial p(x) ~ a, decide the structure ( x - z 1 ) s 1( x - z 2 )s 2. . . ( x - zm )sm implicitly define the coefficient operator G(z) and its Jacobian J(z) - Have an initial guess z 0 to the “pejorative root” - Start the nonlinear least squares iteration zi+1=zi - J(zi )+[ G(zi )-a ], i=0, 1, 2. . . - If it converges verify (i) the backward error || G(z* )-a || (ii) the pejorative condition 1/s - Accept the pejorative root if both are tiny

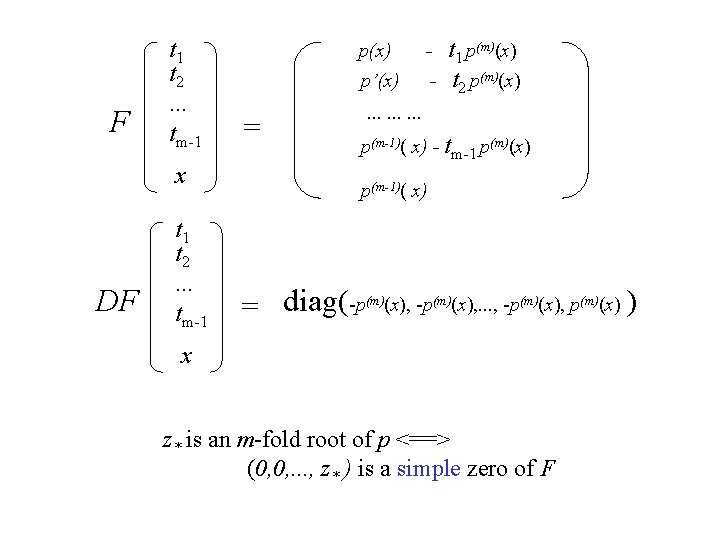
Isolated multiple roots: The polynomial p(x) has an m-fold root p(x) = ( x-z* )m. q(x-z*) The clue: p(z*) = p’(z*) = p”(z*) =. . . = p(m-1)(z*) = 0 p(m)(z*) =/= 0 F t 1 t 2. . . tm-1 x p(x) p’(x) = - t 1 p(m)(x) t 2 p(m)(x) . . p(m-1)( x) - tm-1 p(m)(x) p(m-1)( x)

F t 1 t 2. . . tm-1 x DF t 1 t 2. . . tm-1 p(x) p’(x) = - t 1 p(m)(x) t 2 p(m)(x) . . p(m-1)( x) - tm-1 p(m)(x) p(m-1)( x) = diag(-p(m)(x), . . . , -p(m)(x), p(m)(x) ) x z* is an m-fold root of p <==> (0, 0, . . . , z* ) is a simple zero of F

Theorem: Let p(x) = [( x-z* )m. q(x-z*)] + [em-1(x-z* )m-1 +. . . + e 1(x-z* ) + e 0] Then F has a simple zero t 1 t 2. . . tm-1 z = 0 0. . . 0 + [1/q(0)] z* z = z* + [1/(mq(0))] [em-1] e 0 e 1. . . em-2 em-1/m

Conclusion 1. Ill-condition is cause by a wrong “identity” 2. Multiple roots are pejoratively well conditioned, thereby tractable. 3. Extension of machine precision is not needed, a change in computing concept is. 4. To calculate multiple roots, one has to figure out the multiplicity structure (how? ) Question: Can Jordan Canonical form be computed?