Perfect Matching for Biconnected Cubic Graphs in Onlog

Perfect Matching for Biconnected Cubic Graphs in O(nlog 2 n) Time Krzysztof Diks & Piotr Stańczyk

Petersen theorem (1891) n n Cubic graph without perfect matching contains at least three bridges Conclusion: every biconnected cubic graph has a perfect matching

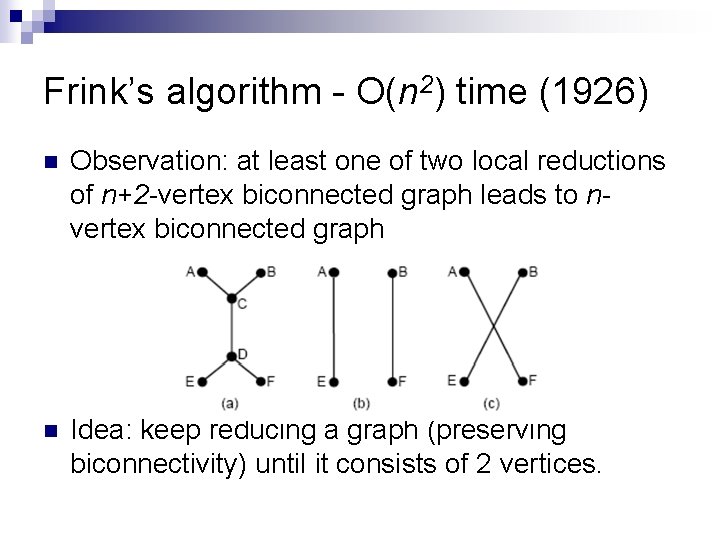
Frink’s algorithm - O(n 2) time (1926) n Observation: at least one of two local reductions of n+2 -vertex biconnected graph leads to nvertex biconnected graph n Idea: keep reducing a graph (preserving biconnectivity) until it consists of 2 vertices.

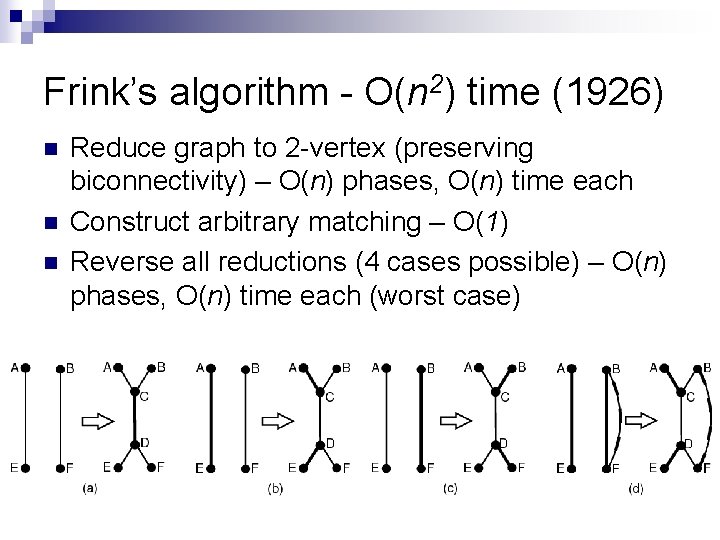
Frink’s algorithm - O(n 2) time (1926) n n n Reduce graph to 2 -vertex (preserving biconnectivity) – O(n) phases, O(n) time each Construct arbitrary matching – O(1) Reverse all reductions (4 cases possible) – O(n) phases, O(n) time each (worst case)

Biedl’s et al. algorithm – O(nlog 4 n) time (SODA, 1999) n Valid reduction selection ¨ n Instead of computing biconnected components from scratch use dynamic graph biconnectivity algorithm – O(log 4 n) per edge removal/addition/query Elimination of case (d) from the revertion process 1) Select an edge e which is excluded from the matching ¨ 2) Perform reductions against edges incident to e (edge e „travels” along the graph) ¨ 3) Construct initial matching excluding edge e ¨ 4) Reverse all reductions – case d) does not occur, as e is never matched ¨ n Complexity: O(nlog 4 n)

New algorithm – O(nlog 2 n) time n Replace dynamic graph biconnectivity algorithm with: Dynamic graph connectivity algorithm – O(log 2 n) deterministic / O(lognloglog 3 n) randomized time ¨ Tarjan’s dynamic trees – O(logn) (addition, removal of edges, change of tree’s root, LCA computation) ¨ n How to perform reduction phase with a new approach?

New algorithm – O(nlog 2 n) time n Remove reduction edge along with all incident vertices / edges. Two cases are possible: ¨ Resulting graph is not connected n n n If so, graph has a structure presented in figure (a) One reduction leads to not connected graph (can be verified with dynamic connectivity algorithm) The other reduction leads to biconnected graph (Frink’s theorem)

New algorithm – O(nlog 2 n) time ¨ Resulting graph is connected n n n Analyze changes in spanning tree maintained by dynamic connectivity data-structure, update Tarjan’s dynamic trees Analyze edges of a spanning tree T spanned by vertices A, B, E and F. Select reduction which covers all spanned edges with cycles (use LCA operation from Tarjan’s trees) Selected reduction maintains biconnectivity…

New algorithm – O(nlog 2 n) time n Selected reduction maintains biconnectivity: ¨ Added edges and edges spanned by A, B, C and D are covered by a cycle ¨ Any other edge e → before reduction there was a cycle c covering e. n n If c is a cycle in reduced graph → OK Otherwise, c contains some removed edges E. Let f be a cycle in T+E containing all edges of E. Symmetric difference of f and c is a cycle in reduced graph ¨ Each edge belongs to some cycle → graph is biconnected n Overall complexity: O(nlog 2 n) deterministic, O(nloglog 3 n) randomized

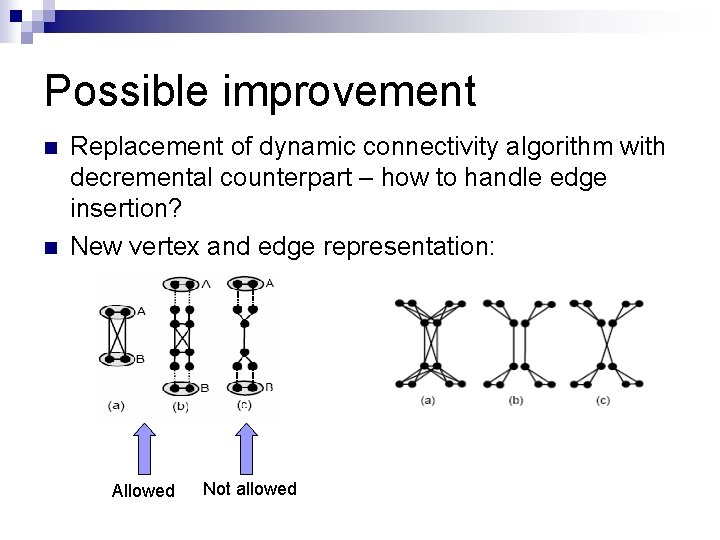
Possible improvement n n Replacement of dynamic connectivity algorithm with decremental counterpart – how to handle edge insertion? New vertex and edge representation: Allowed Not allowed

Possible improvement n It is not allowed to perform reductions against not allowed edges – how to bypass it… Introduce support for reverse points in decremental connectivity data-structure ¨ In case of performing reduction against not allowed edge, it is required to execute reverse point first, three cases are possible… ¨

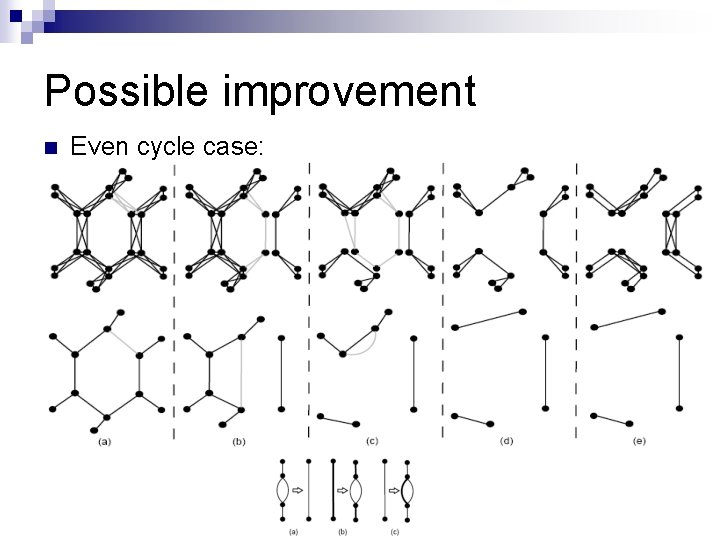
Possible improvement n Even cycle case:

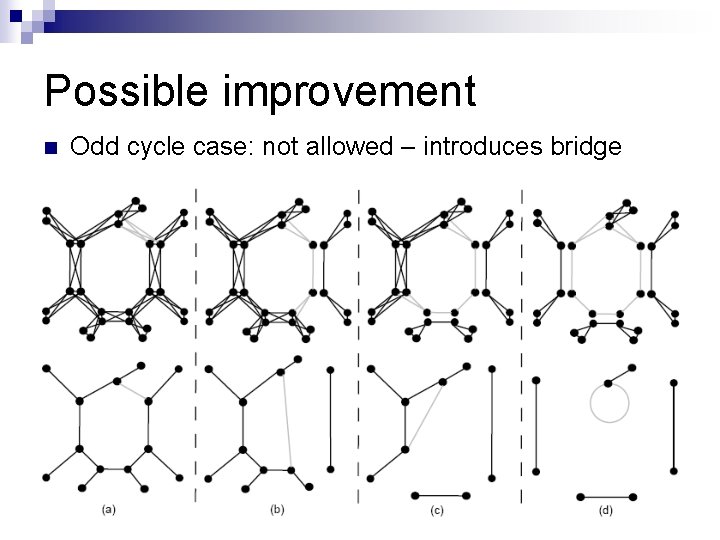
Possible improvement n Odd cycle case: not allowed – introduces bridge

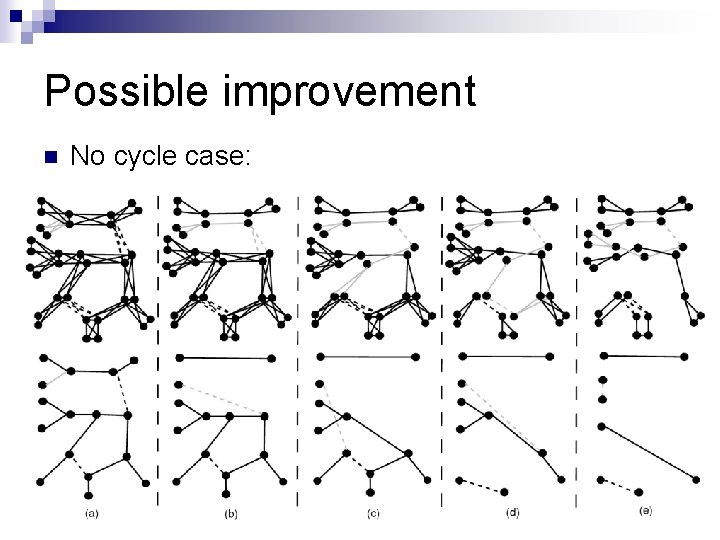
Possible improvement n No cycle case:

Thank you n Any questions?