Perceptually Based Methods for Robust Image Hashing Vishal

Perceptually Based Methods for Robust Image Hashing Vishal Monga Committee Members: Prof. Ross Baldick Prof. Brian L. Evans (Advisor) Prof. Wilson S. Geisler Prof. Joydeep Ghosh Prof. John E. Gilbert Prof. Sriram Vishwanath Ph. D. Qualifying Exam Communications, Networks, and Systems Area Dept. of Electrical and Computer Engineering The University of Texas at Austin April 14 th , 2004 1

Outline • Introduction • Related work – – – Digital signature techniques for image authentication Robust feature extraction from images Open research issues • Expected contributions – – – Framework for robust image hashing using feature points Clustering algorithms for feature vector compression Image authentication under geometric attacks via structure matching • Conclusion 2

Introduction Hash Example • Hash function: Projects value from set with large (possibly infinite) number of members to set with fixed number of (fewer) members in irreversible manner – Provides short, simple representation of large digital message Database name search example – Name Hash Value Ghosh Monga Baldick Vishwanath Evans Geisler Gilbert 1 2 3 3 5 5 6 Hash Scheme – Sum of ASCII codes of characters in a name computed modulo N (= 7) a prime number 3

Introduction Image Hashing: Motivation • Hash functions – Fixed length binary string extracted from a message – Used in compilers, database searching, cryptography – Cryptographic hash: security applications e. g. message authentication, ensuring data integrity • Traditional cryptographic hash – Not suited for multimedia very sensitive to input, i. e. change in one input bit changes output dramatically • Need for robust perceptual image hashing – Perceptual: based on human visual system response – Robust: hash values for “perceptually identical” images must be the same (with a high probability) 4

Introduction Image Hashing: Motivation • Applications – Image database search and indexing – Content dependent key generation for watermarking – Robust image authentication: hash must tolerate incidental modifications yet be sensitive to content changes JPEG Compressed Original Image Same hash value h 1 Tampered Different hash values h 2 5

Introduction Perceptual Hash: Desirable Properties • Perceptual robustness • Fragility to distinct inputs • Randomization Symbol H(I) Isim Idiff – Necessary in security applications to minimize vulnerability against malicious attacks m Meaning Hash value extracted from image I Image identical in appearance to I Image clearly distinct in appearance w. r. t I Length of hash (in bits) 6

Outline • Introduction • Related work – – – Digital signature techniques for image authentication Robust feature extraction from images Open research issues • Expected contributions – – – Framework for robust image hashing using feature points Clustering algorithms for feature vector compression Image authentication under geometric attacks via structure matching • Conclusion 7

Related Work Content Based Digital Signatures • Goal – Authenticate image based on extracted signature • Image statistics based on – Intensity histograms of image blocks [Schneider et al. , 1996] – mean, variance and kurtosis of intensity values extracted from image blocks and compare then to statistics of reference image [Kailasanathan et al. , 2001] • Drawbacks – Easy to modify the image without altering its intensity histogram scheme is less secure – Intensity statistics can be altered easily without significantly changing the image appearance 8

Related Work Content Based Digital Signatures… • Feature point based methods – Wavelet based corner detection [Bhatacherjee et al. , 1998] – Canny edge detection [Dittman et al. , 1999] – Apply public key encryption on the features to arrive at the digital signature • Relation based methods [Lin & Chang 2001] – Invariant relationship between discrete cosine transform (DCT) coefficients of two different blocks • Common characteristic of above methods – work well for some attacks viz. JPEG compression – still sensitive to several incidental modifications that do not alter the image appearance 9

Related Work Robust Image Hashing: Method # 1 • Image statistics vector from wavelet decomposition of image [Venkatesan et al. , 2000] – Averages of wavelet coefficients in coarse sub-bands and variances in other sub-bands Vertical freqs. Horizontal freqs. Diagonal freqs. Coarse Details Extract Statistics Vector and Quantize [00100101 | 01110100|1…………… 00111001 | 001010] Error Correction Decoding [00100101…… 011] Hash Value 10

Related Work Robust Image Hashing: Method # 2 • Preserve magnitude of low frequency DCT coefficients [Fridrich et al. , 2001] – Survives JPEG compression, linear filtering attacks – Very sensitive to geometric distortions (local & global) • Randomize using a secret key K – Generate N random smooth patterns P(i), i = 1, …, N – Take vectorized dot product of low frequency DCT coefficients (in block B) with random patterns and use threshold Th to obtain N bits bi Back 11

Related Work Robust Image Hashing: Method # 3 • Invariance of coarse wavelet coefficients [Mihcak et al. , 2001] DC sub-band • Key observation – Main geometric features of image stay invariant under small perturbations to image • Hash algorithm 3 - level Haar wavelet decomposition – Threshold wavelet coefficients of DC sub-band (coarse robust features) to obtain a binary matrix – Perform filtering and re-thresholding to iteratively arrive at binary map which is then used as the hash – Iterative procedure is designed so as to preserve significant image geometry Back 12

Related Work Robust Digital Signature: Method # 4 • Interscale relationship of wavelet coefficients [Lu & Liao, 2003] – Magnitude difference between a parent node and its four child nodes is difficult to destroy (alter) under content-preserving manipulations – wavelet scale, o – orientation, 0 ≤ i, j ≤ 1 w 0, 0(x, y) w 1, 0(2 x, 2 y) w 1, 1(2 x+1, 2 y) w 1, 2(2 x, 2 y+ 1) w 1, 3(2 x+1, 2 y+1) 2 -D wavelet decomposition tree 13

Related Work Open Issues Contribution 1 • A robust feature point scheme for hashing – – – Inherent sensitivity to content-changing manipulations e. g. could be useful in authentication Representation of image content robust to both global and local geometric distortions Contribution 3 Preferably use properties of the human visual system Contribution 1 • Trade-offs in image hashing – – Contribution 2 Robustness vs. Fragility, Randomness Question: Minimum length of the final hash value (binary string) needed to meet the above goals ? • Randomized algorithms for secure image hashing Contribution 2 14

Outline • Introduction • Related Work – – – Digital signature techniques for Image Authentication Robust feature extraction from Images Open research issues • Expected contributions – – – Framework for robust image hashing using feature points Clustering algorithms for feature vector compression Image authentication under geometric attacks via structure matching • Conclusion 15

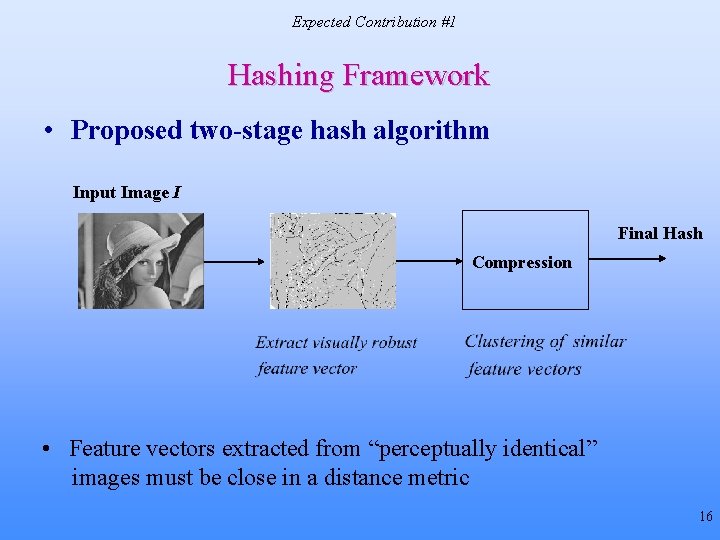
Expected Contribution #1 Hashing Framework • Proposed two-stage hash algorithm Input Image I Final Hash Compression • Feature vectors extracted from “perceptually identical” images must be close in a distance metric 16

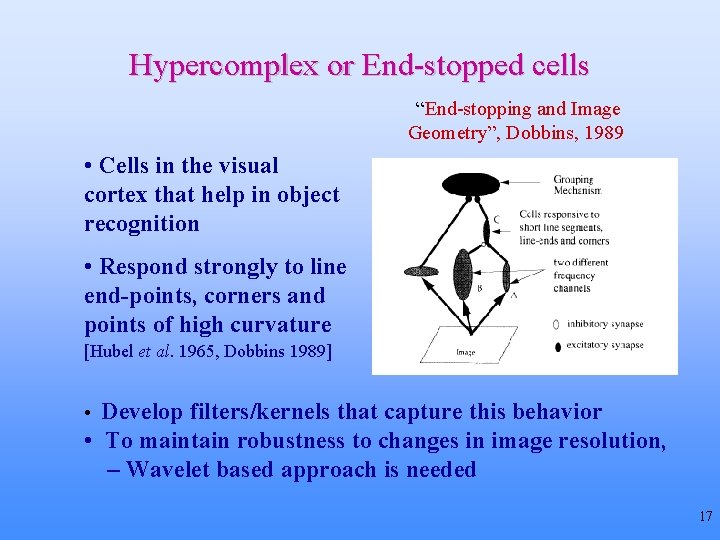
Hypercomplex or End-stopped cells “End-stopping and Image Geometry”, Dobbins, 1989 • Cells in the visual cortex that help in object recognition • Respond strongly to line end-points, corners and points of high curvature [Hubel et al. 1965, Dobbins 1989] • Develop filters/kernels that capture this behavior • To maintain robustness to changes in image resolution, – Wavelet based approach is needed 17

End-Stopped Wavelet Basis • Morlet wavelets [Antoine et al. , 1996] – To detect linear (or curvilinear) structures having a specific orientation x – (x, y) 2 -D spatial co-ordinates ko – (k 0, k 1) wave-vector of the mother wavelet Orientation control - • End-stopped wavelet [Vandergheynst et al. , 2000] – Apply First Derivative of Gaussian (FDo. G) operator to detect end-points of structures identified by Morlet wavelet 18

End-Stopped Wavelets…Example • Morlet Wavelet along the u-axis – Detects vertically oriented linear structures • FDo. G operator along frequency axis v – Applied on the Morlet wavelet to detect end-points and corners Synthetic L-shaped image Response of Morlet wavelet, orientation = 0 degrees Response of the end-stopped wavelet 19

Expected Contribution #1 Computing Wavelet Transform • Generalize end-stopped wavelet • Employ the wavelet family – – – Scale parameter = 2, i – scale of the wavelet Discretize orientation range [0, π ] into M intervals i. e. θk = (k π/M ), k = 0, 1, … M - 1 • Finally, the wavelet transform is given by 20

Expected Contribution #1 Proposed Feature Detection Method [Monga & Evans, 2004] 1. Compute wavelet transform at suitably chosen scale i for several different orientations 2. Significant feature selection: Locations (x, y) in the image that are identified as candidate feature points satisfy 3. Avoid trivial (and fragile) features: Qualify a location as a final feature point if • Randomization: Partition the image into N random regions using a secret key K, extract features from each random region • Probabilistic Quantization: Quantize feature vector based on distribution (histogram) of image feature points to enhance robustness 21

Expected Contribution #1 Iterative Feature Extraction Algorithm [Monga & Evans, 2004] 1. Extract feature vector f of length P from image I, quantize f probabilistically to obtain a binary string bf 1 (increase count*) 2. Remove “weak” image geometry: Compute 2 -D order statistics (OS) filtering of I to produce Ios = OS(I; p, q, r) 3. Preserve “strong” image geometry: Perform low-pass linear shift invariant (LSI) filtering on Ios to obtain Ilp 4. Repeat step 1 with Ilp to obtain bf 2 5. IF (count = Max. Iter) go to step 6. Max. Iter, ρ and P are algorithm parameters. * count = 0 to begin with ELSE IF D(bf 1, bf 2) < ρ go to step 6. fv(I) denotes quantized feature ELSE set I = Ilp and go to step 1. 6. Set fv(I) = bf 2 vector D(. , . ) – normalized Hamming distance between its arguments 22

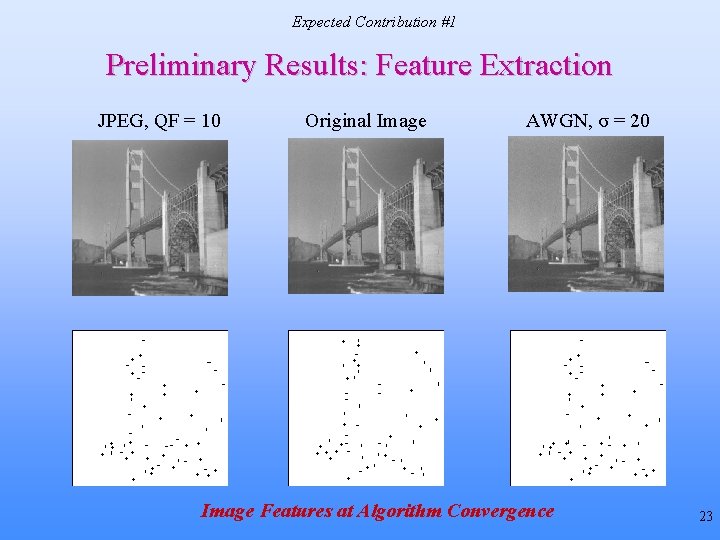
Expected Contribution #1 Preliminary Results: Feature Extraction JPEG, QF = 10 Original Image AWGN, σ = 20 Image Features at Algorithm Convergence 23

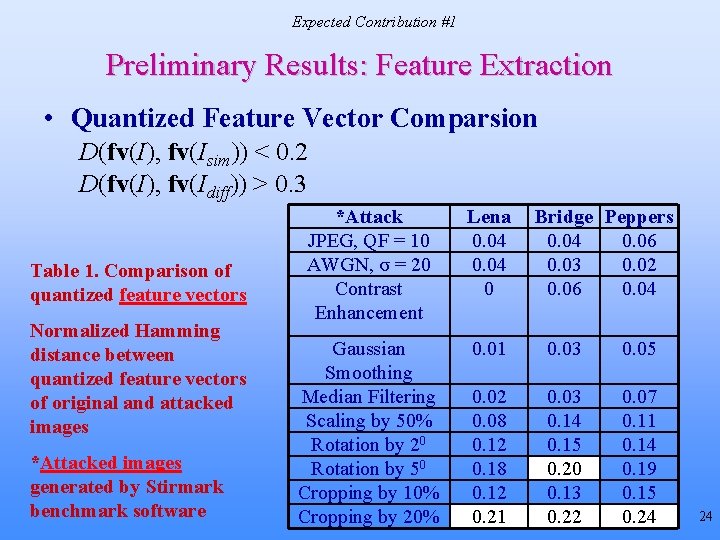
Expected Contribution #1 Preliminary Results: Feature Extraction • Quantized Feature Vector Comparsion D(fv(I), fv(Isim)) < 0. 2 D(fv(I), fv(Idiff)) > 0. 3 Table 1. Comparison of quantized feature vectors Normalized Hamming distance between quantized feature vectors of original and attacked images *Attacked images generated by Stirmark benchmark software *Attack JPEG, QF = 10 AWGN, σ = 20 Contrast Enhancement Lena 0. 04 0 Bridge Peppers 0. 04 0. 06 0. 03 0. 02 0. 06 0. 04 Gaussian Smoothing Median Filtering Scaling by 50% Rotation by 20 Rotation by 50 Cropping by 10% Cropping by 20% 0. 01 0. 03 0. 05 0. 02 0. 08 0. 12 0. 18 0. 12 0. 21 0. 03 0. 14 0. 15 0. 20 0. 13 0. 22 0. 07 0. 11 0. 14 0. 19 0. 15 0. 24 24

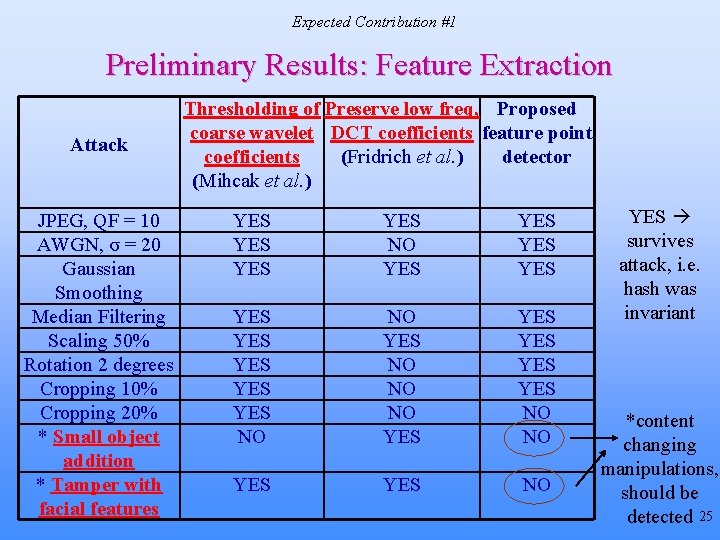
Expected Contribution #1 Preliminary Results: Feature Extraction Attack JPEG, QF = 10 AWGN, σ = 20 Gaussian Smoothing Median Filtering Scaling 50% Rotation 2 degrees Cropping 10% Cropping 20% * Small object addition * Tamper with facial features Thresholding of Preserve low freq, Proposed coarse wavelet DCT coefficients feature point coefficients (Fridrich et al. ) detector (Mihcak et al. ) YES YES NO YES YES YES NO NO NO YES YES YES NO NO YES survives attack, i. e. hash was invariant *content changing manipulations, should be detected 25

Expected Contribution # 1 Highlights • Framework for image hashing using feature points – – Two stage hash algorithm Any visually robust feature point detector is a good candidate to be used with the iterative algorithm • Trade-offs facilitated – – Robustness vs. Fragility: select feature points such that T 1, T 2 large enough ensures that features are retained in several attacked versions of the image, else removed easily Robustness vs. Randomization: number of random regions Until N < Nmax, robustness largely preserved else random regions shrink to the extent that they do not contain significant chunks of image geometry 26

Expected Contribution # 2 Feature Vector Compression • Goals in compressing to a final hash value – – – Cancel small perturbations between feature vectors of “perceptually identical” images Maintain fragility to distinct inputs Retain and/or enhance randomness properties for secure hashing • Problem statement: Retain perceptual significance – Let (li, lj) denote vectors in the metric space of feature vectors V and 0 < ε < δ, then it is desired 27

Expected Contribution # 2 Possible Solutions • Error correction decoding [Venkatesan et al. , 2000] – – Applicable to binary feature vectors Break the vector down to segments close to the length of codewords in a suitably chosen error-correcting code • More generally vector quantization/clustering – Minimize an “average distance” to achieve compression close to the rate distortion limit – P(l) – probability of occurrence of vector l, D(. , . ) distance metric defined on the feature vectors ck – codewords/cluster centers, Sk – kth cluster – 28

Expected Contribution # 2 Is Average Distance the Appropriate Cost for the Hashing Application? • Problems with average distance VQ – – – No guarantee that “perceptually distinct” feature vectors indeed map to different clusters – no straightforward way to trade-off between the two goals Must decide number of codebook vectors in advance Must penalized some errors harshly e. g. if vectors really close are not clustered together, or vectors very far apart are compressed to the same final hash value • Define alternate cost function for hashing – Develop clustering algorithm that tries to minimize that cost 29

Expected Contribution # 2 Cost Function for Feature Vector Compression • Define joint cost matrices C 1 and C 2 (n x n) α > 0, Г > 1 are algorithm parameters – n – total number of vectors be clustered, C(li), C(lj) denote the clusters that these vectors are mapped to • Exponential cost – Ensures that severe penalty is associated if feature vectors far apart and hence “perceptually distinct” are clustered together 30

Expected Contribution # 2 Cost Function for Feature Vector Compression • Further define S 1 as • Normalize to get *S 2 is defined similarly , • Then, minimize the “expected” cost – p(i) = p(li), p(j) = p(lj) 31

Expected Contribution # 3 Image Authentication Under Geometric Attacks • Basic premise – – Feature points of a reference image and a geometrically attacked image are related by a suitable transformation Affine transformation models the geometric distortion x = (x 1, x 2) , y = (y 1, y 2) R – 2 x 2 matrix, t – 2 x 1 vector • Hausdorff distance to compare feature points from two images [Atallah, 1983; Rote 1991] – – Used in computer vision for locating objects in an image Relatively insensitive to perturbations in feature points, can tolerate errors due to occlusion or feature detector failure 32

Expected Contribution # 3 Image Authentication Under Geometric Attacks • Hausdorff distance between point sets A and B – A = {a 1, …, ap} and B = {b 1, …, bq} where – Measures degree of mismatch between two sets • Employ structure matching algorithms [Huttenlocher et al. 1993, Rucklidge 1995] – To determine G such that – Here, fr and fc denote feature point sets from reference and candidate image to be authenticated 33

Conclusion & Future Work • Feature point based hashing framework ü Iterative feature detector that preserves significant image geometry, features invariant under several attacks ü Trade-offs facilitated between hash algorithm goals • Algorithms for feature vector compression ü Novel cost function for the hashing application – Heuristic clustering algorithm(s) to minimize this cost – Randomized clustering for secure hashing • Image authentication under geometric attacks ü Affine transformation to model geometric distortions – Hausdorff distance and structure matching algorithms to determine affine transformation and authenticate 34

Conclusion Proposed Schedule Semester Work Plan Summer 2004 Perform extensive tests on the feature extraction algorithm, implement the solution to stage 1 Fall 2004 Develop and finalize the clustering algorithm for feature vector compression. Compare with other approaches viz. error correction decoding Spring 2005 Finalize the design and implement the scheme for image authentication under geometric attacks Summer 2005 Implement the two-step hash algorithm Fall 2005 Write and defend dissertation 35

Backup Slides 36

Introduction Hash: Illustrative Example • Parsing in compiling a program • Variable names kept in a data structure – Array of pointers, each pointer points to a linked list – Index into the array is a hash value • Example: variable name “university” Hashing Scheme – Sum of ASCII codes of characters in a variable name computed modulo N a prime number – Check linked list at array index, add string to linked list if it had not been previously parsed – 37

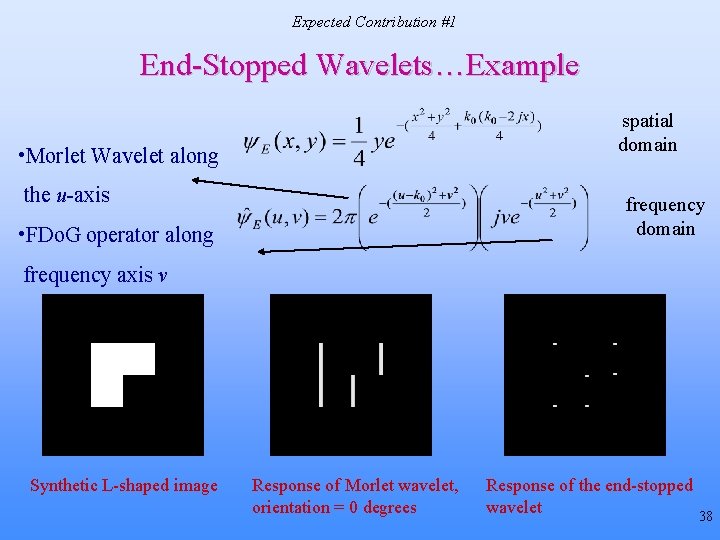
Expected Contribution #1 End-Stopped Wavelets…Example spatial domain • Morlet Wavelet along the u-axis frequency domain • FDo. G operator along frequency axis v Synthetic L-shaped image Response of Morlet wavelet, orientation = 0 degrees Response of the end-stopped wavelet 38

Feature Detection Back Content Changing Manipulations Original image Maliciously manipulated image 39

Results Algorithm Parameters • Image Conditioning – – All images resized to 512 x 512 via triangular interpolation prior to feature extraction Intensity planes of color images were used • Pixel neighborhood – – Circular to detect isotropic features Radius of 5 pixels • Iterative Feature Extraction – – wavelet scale, i = 3 Max. Iter = 20, ρ = 0. 001, P = 128 LSI filter: zero-phase low pass filter (11 x 11) designed Back using Mc. Cllelan transformations Order statistics filtering: median with 5 x 5 window 40

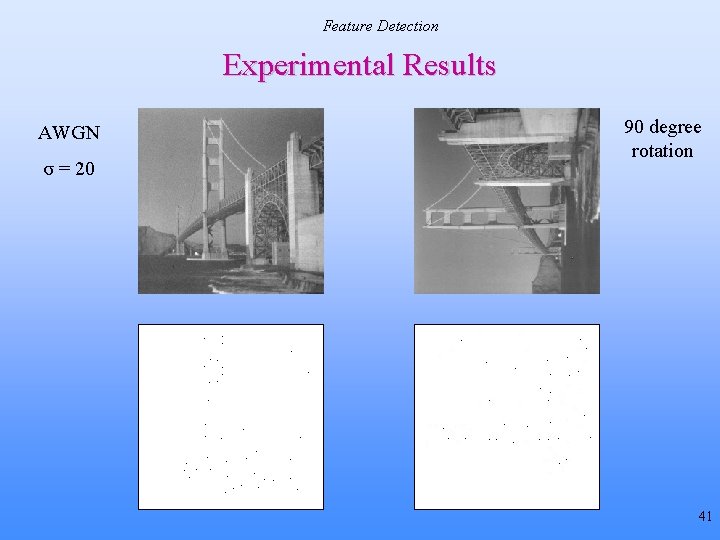
Feature Detection Experimental Results AWGN σ = 20 90 degree rotation 41

Expected Contribution # 1 Trade-offs • Perceptual robustness vs. fragility – – – Size of the search neighborhood: large feature points are more robust Select feature points such that T 1, T 2 large enough implies features retained in several attacked versions of the image else removed easily • Robustness vs. Randomization – Uptil N < Nmax, robustness largely retained else random regions shrink to the extent that they do not contain significant chunks of image geometry Back 42

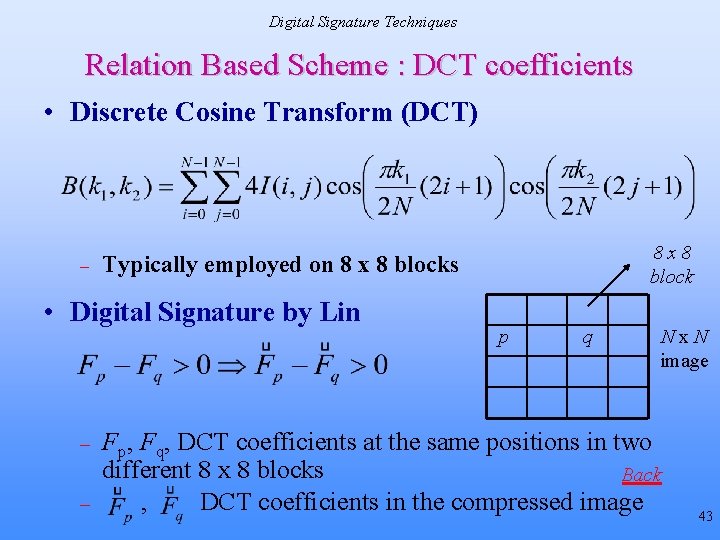
Digital Signature Techniques Relation Based Scheme : DCT coefficients • Discrete Cosine Transform (DCT) – • Digital Signature by Lin – – 8 x 8 block Typically employed on 8 x 8 blocks p q Nx. N image Fp, Fq, DCT coefficients at the same positions in two different 8 x 8 blocks Back , DCT coefficients in the compressed image 43

Wavelet Decomposition Multi-Resolution Approximations 44

Back 45

Wavelet Decomposition Back Examples of Perceptually Identical Images Original Image JPEG, QF = 10 Contrast Enhanced 10% cropping 2 degree rotation 3 degree rotation 46

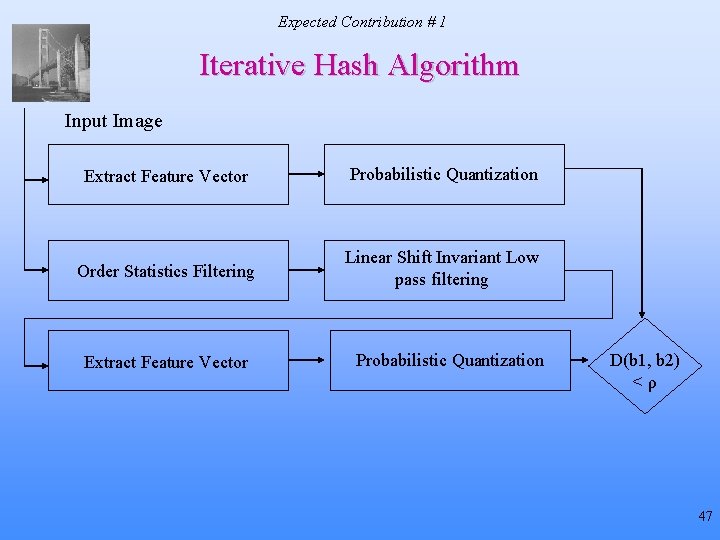
Expected Contribution # 1 Iterative Hash Algorithm Input Image Extract Feature Vector Probabilistic Quantization Order Statistics Filtering Linear Shift Invariant Low pass filtering Extract Feature Vector Probabilistic Quantization D(b 1, b 2) <ρ 47

Quantization Probabilistic Quantization • Feature Vector – fmn = m + H*n • Quantization Scheme – L quantization levels Design quantization bins [li, li-1) such that – Quantization Rule – Back 48

Feature Detection Feature Vector Extraction • Randomization – Partition the image into N regions using k-means segmentation – extract feature points from each region – Secret key K is used to generate initial guesses for the clusters (centroids of random regions) Avoid very small regions since they would not yield robust image features – Back 49

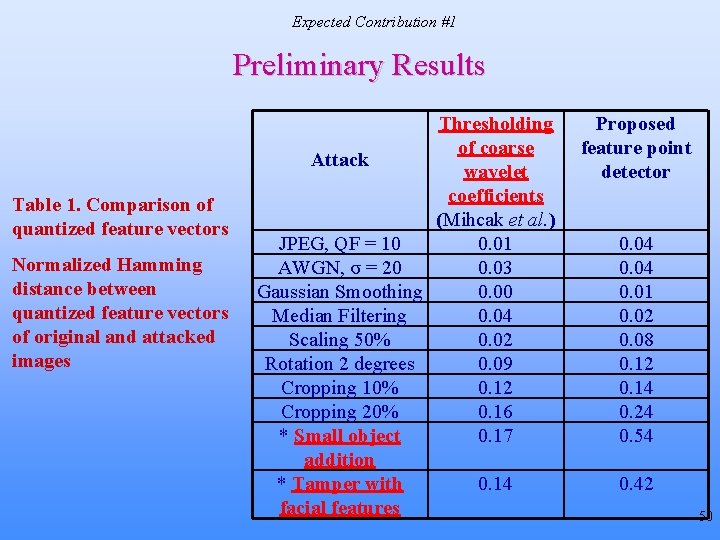
Expected Contribution #1 Preliminary Results Table 1. Comparison of quantized feature vectors Normalized Hamming distance between quantized feature vectors of original and attacked images Thresholding of coarse Attack wavelet coefficients (Mihcak et al. ) JPEG, QF = 10 0. 01 AWGN, σ = 20 0. 03 Gaussian Smoothing 0. 00 Median Filtering 0. 04 Scaling 50% 0. 02 Rotation 2 degrees 0. 09 Cropping 10% 0. 12 Cropping 20% 0. 16 * Small object 0. 17 addition * Tamper with 0. 14 facial features Proposed feature point detector 0. 04 0. 01 0. 02 0. 08 0. 12 0. 14 0. 24 0. 54 0. 42 50

Clustering Algorithms Minimizing the Cost • Decision Version of the Clustering Problem – – For a fixed number of clusters k, is there a clustering with cost less than a constant? Shown to be NP-complete via a reduction from the k-way graph cut problem [Monga et. al, 2004] • Polynomial time greedy heuristic to solve the problem – – – Select cluster centers based on probability mass of vectors in V – minimize error probabilities in a rigorous sense Trade-offs: Exclusive minimization of would compromise and vice-versa Basic algorithm with variations to facilitate trade-offs 51

Clustering Algorithms Basic Clustering Algorithm 1. Obtain ε, δ, set k = 1. Select the data point associated with the highest probability mass, label it l 1 2. Make the first cluster by including all unclustered points lj such that D(l 1, lj) < ε/2 3. k = k + 1. Select the highest probability data point lk amongst the unclustered points such that where S is any cluster, C – set of clusters formed till this step and 4. Form the kth cluster Sk by including all unclustered points lj such that D(lk, lj) < ε/2 5. Repeat steps 3 -4 till no more clusters can be formed 52

Clustering Algorithms Visualization of the Clustering Algorithm 53

Clustering Algorithms Observations • For any (li, lj) in cluster Sk • No errors till this stage of the algorithm – – – Each cluster is atleast ε away from any other cluster and hence there are no errors by violating (1) Within each cluster the maximum distance between any two points is at most ε, and because 0 < ε < δ there are no errors by violation of (2) The data points that are left unclustered are atleast 3 ε /2 away from each of the existing clusters • Next – Two different approaches to handle the unclustered points 54

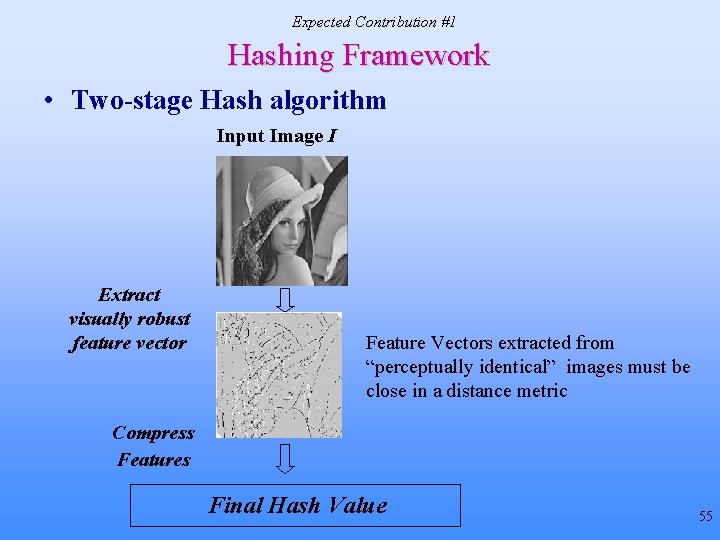
Expected Contribution #1 Hashing Framework • Two-stage Hash algorithm Input Image I Extract visually robust feature vector Feature Vectors extracted from “perceptually identical” images must be close in a distance metric Compress Features Final Hash Value 55

Clustering Algorithms Approach 1 1. Select the data point l* amongst the unclustered data points that has the highest probability mass 2. For each existing cluster Si, i = 1, 2, …, k compute Let S(δ) = {Si such that di ≤ δ} 3. IF S(δ) = {Φ} THEN k = k + 1. Sk = l* is a cluster of its own ELSE for each Si in S(δ) define where denotes the complement of Si i. e. all clusters in S(δ) except Si. Then, l* is assigned to the cluster S* = arg min F(Si) 4. Repeat steps 1 through 3 till all data points are exhausted 56

Clustering Algorithms Approach 2 1. Select the data point l* amongst the unclustered data points that has the highest probability mass 2. For each existing cluster Si, i = 1, 2, …, k define and β lies in [1/2, 1] where denotes the complement of Si i. e. all existing clusters except Si. Then, l* is assigned to the cluster S* = arg min F(Si) 3. Repeat steps 1 and 2 till all data points are exhausted 57

Clustering Algorithms Summary • Approach 1 – Tries to minimize conditioned on =0 Smoothly trades off the minimization of via the parameter β β = ½ joint minimization β = 1 exclusive minimization of vs. • Approach 2 – – – • Final Hash length determined automatically! – – Given by bits, where k is the total number of clusters formed Proposed clustering can be used to compress feature vectors in any metric space e. g. euclidean, hamming 58

Clustering Algorithms Randomized Clustering for Secure Hashing • Heuristic for the deterministic map – Select the highest probability data point amongst the unclustered data points • Randomization Scheme – Normalize the probabilities of the existing unclustered data points to define a new probability mass such that where i runs over unclustered points, – Employ a uniformly distributed random variable in [0, 1] (generated via a secret key) to select the data point i as a cluster center with probability 59

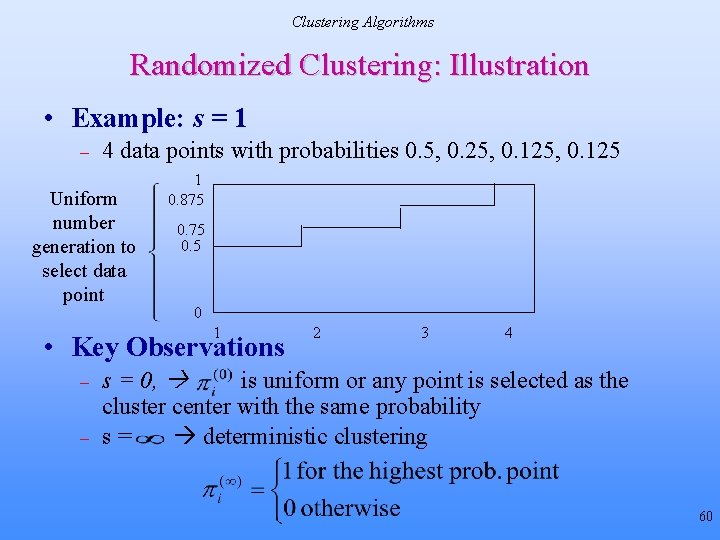
Clustering Algorithms Randomized Clustering: Illustration • Example: s = 1 – 4 data points with probabilities 0. 5, 0. 25, 0. 125 Uniform number generation to select data point 1 0. 875 0. 5 0 1 • Key Observations – – 2 3 4 s = 0, is uniform or any point is selected as the cluster center with the same probability s= deterministic clustering 60

Clustering Algorithms Clustering: Results • Compress binary feature vector of L = 240 bits – Final hash length = 46 bits, with Approach 2, β = 1/2 Clustering Algorithm Approach 1 7. 64 * 10 -8 0 Approach 2, β = ½ 7. 43 * 10 -9 7. 464 * 10 -10 Approach 2, β = 1 7. 17 * 10 -9 4. 87 * 10 -9 *Average distance VQ 5. 96 * 10 -4 3. 65 * 10 -5 • *Average distortion VQ at the same rate – Value of cost function is orders of magnitude lower for the proposed clustering 61

Clustering Algorithms Conclusion & Future Work • Perceptual Image Hashing via Feature Points – – – Extract Feature Points that preserve significant image geomtery Based on properties of the Human Visual System (HVS) Robust to local and global geometric distortions • Clustering Algorithms for compression – – Randomized to minimize vulnerability against malicious attacks generated by an adversary Trade-offs facilitated between robustness and randomness, fragility • Future Work – – Authentication under geometric attacks Information theoretically secure hashing 62

Image Hashing Via Feature Points Perceptual Image Hashing Via Feature Points • Feature Points are required to be invariant across “perceptually identical” images – – – Primary geometric features of the image are largely preserved under small perturbations [Mihcak et. al, 2001] i. e. extract significant image geometry preserving feature points Identify what the human eye perceives as “robust” or “invariant” geometric features • Edge based detection is not suited – – Has problems with high compression ratios, quantization and scaling [Zheng and Chellapa, 1993] Human recognition performance does not impede even when much edge information is lost [Beiderman, 1987] 63

End-stopping and image features ES 2 Wavelet • Example Wavelets – SDo. G operator on the morlet wavelet • Wavelet behavior – produces a strong response at the center of any oriented linear stimuli of a particular length determined by σ 64

Clustering Algorithms Clustering: Dependence on source distribution • Source distributions may be very “skewed” – – Trivial clusters may be formed i. e. with very low probability points included For efficient compression, the number of clusters formed should accurately represent the statistics of the source • Solution – – – Consider the algorithm when m clusters are formed m < k and i < n points already clustered Assign remaining points i. e. {i + 1, …, n} to the remaining clusters in a fashion similar to the basic algorithm Compare the expected cost of this clustering vs. the one with k clusters as formed by the algorithm described before, if the increase is not significant terminate with the current number of clusters 65