Perceptrony o duym marginesie bdu Wykad 10 Wodzisaw

Perceptrony o dużym marginesie błędu Wykład 10 Włodzisław Duch Katedra Informatyki Stosowanej UMK Google: W. Duch

Co było • Perceptron jednowarstwowy. • Uczenie się perceptronów • Demo w Neuro. Solutions

Co będzie • Nieliniowa reguła delta • Adatron • Perceptron wielowarstwowy

Perceptron dla M klas Reguła uczenia perceptronu: • skończona liczba kroków • sensowna generalizacja Granice decyzji perceptronu: dla klasy Ci wyjście gi(X) Decyzja: maxi gi(X), więc na granicy gi(X)=gj(X) Dla M klas jest M(M – 1)/2 granic; część jest redundantna. Obszary decyzyjne – zawsze wypukłe. Klasa Ci, wymagane gi(X)= 1, gj(X)= 0 Niektóre obszary – niesklasyfikowane bo wszystkie gi(X)= 0 lub kilka gi(X)=1 Przykład: granice decyzji perceptronu dla 3 klas.

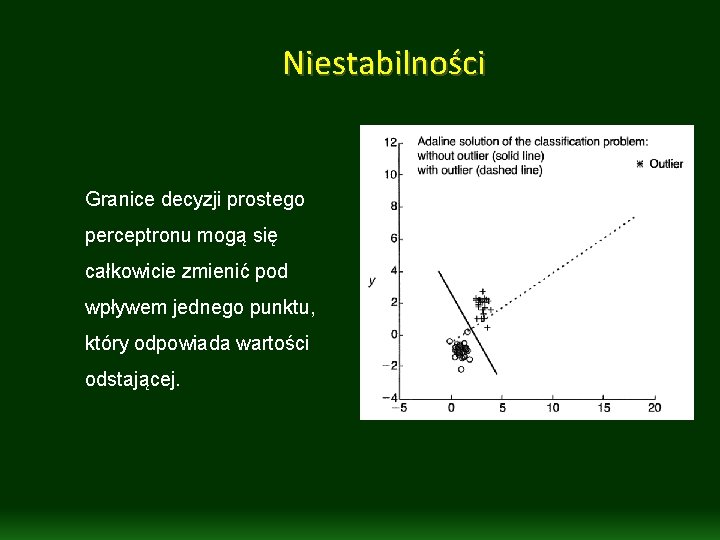
Niestabilności Granice decyzji prostego perceptronu mogą się całkowicie zmienić pod wpływem jednego punktu, który odpowiada wartości odstającej.

Reguła delta - nieliniowa Uczenie zgodne z regułą perceptronu: skoki, niestabilne granice. Błąd przy prezentacji pary (Xp, Yp) dla jednego perceptronu: Funkcja błędu: Szukamy minimum błędu ze względu na Wi

Reguła delta cd. Poprawki do wag: Dla funkcji logistycznej Dla tangh Przykłady działania takiej reguły w Neurosolutions: trening 10 perceptronów do rozpoznawania cyfr (każdy cyfra-reszta); efekty dodawania szumu do znaków – granice się poprawiają!

Adatron i maksymalizacja marginesu Cel: maksymalizacja odległości granicy decyzji od danych. Trening z szumem regularyzacji – prosty, ale kosztowny. Dla 2 klas i funkcji liniowej WX+b marginesy powinny być jak największe by zapewnić generalizację. Znajdź wektor najbliższy granicy i wagi zwiększające margines. Rozwiązanie: • • liniowe - Adatron nieliniowe - SVM (Support Vector Machines)

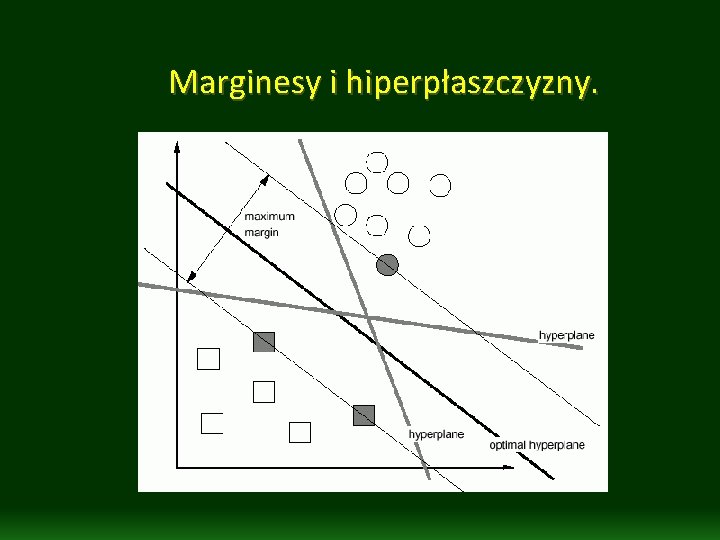
Marginesy i hiperpłaszczyzny.

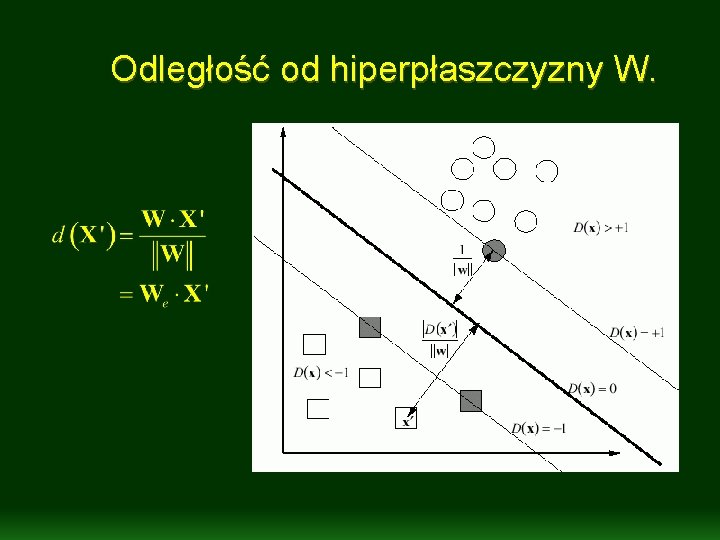
Odległość od hiperpłaszczyzny W.

Adatron: algorytm Przyjmijmy (Xi, Yi), i=1. . N, oraz Yi = ± 1 Progowe neurony, f(X)=sgn(g(X; W, b)) = sgn(W·X+b) Margines rośnie dla min ||W|| pod warunkiem poprawnej klasyfikacji. Problem można sformułować jako minimalizację bez ograniczeń; ai = mnożniki Lagrange’a; f. dyskryminująca jest liniową kombinacją iloczynów

Adatron: algorytm cd. Wstawiając za W i b poprzednie wartości Adatron minimalizuje: dodatkowe warunki Zdefiniujmy pomocnicze funkcje (najpierw policzmy il. skalarne): Algorytm iteracyjny: start a = 0. 1, h, t = 0. 01 mały próg czyli Xi jest odsunięte od granicy Jeśli ai + Dai 0 to zmień lub jeśli < 0 nic nie zmieniaj.

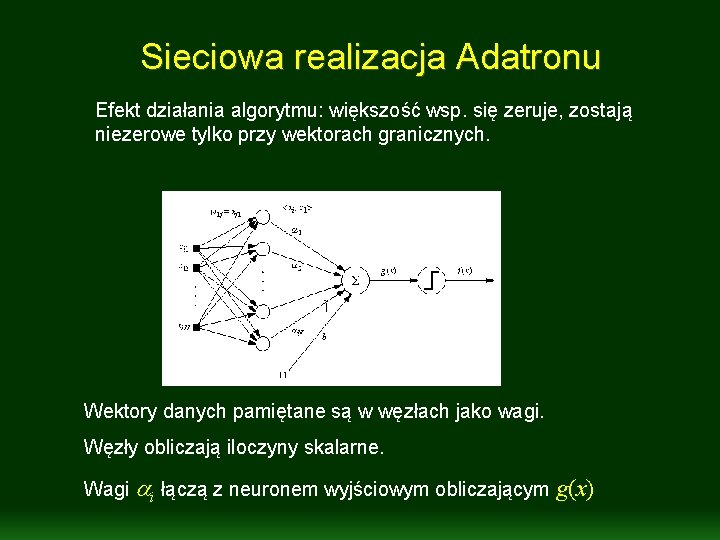
Sieciowa realizacja Adatronu Efekt działania algorytmu: większość wsp. się zeruje, zostają niezerowe tylko przy wektorach granicznych. Wektory danych pamiętane są w węzłach jako wagi. Węzły obliczają iloczyny skalarne. Wagi ai łączą z neuronem wyjściowym obliczającym g(x)

Adatron – efekty • • Tyko pary klas są rozróżniane; potrzeba m(m-1)/2 klasyfikatorów dla m klas, lub dla rozróżnienia 1 reszta tylko m. • Wektory, dla których ai >0 to wektory brzegowe (Support Vectors). • Uczenie – na końcu procesu głównie w pobliżu granic decyzji. • Złożoność O(n 2) redukuje się do O(nsv 2) • Złożoność minimalizacji – eksponencjalna w N (wymiar wektora). • Rezultaty podobne jak z perceptronem z gładką funkcja zamiast skokowej (znaku).

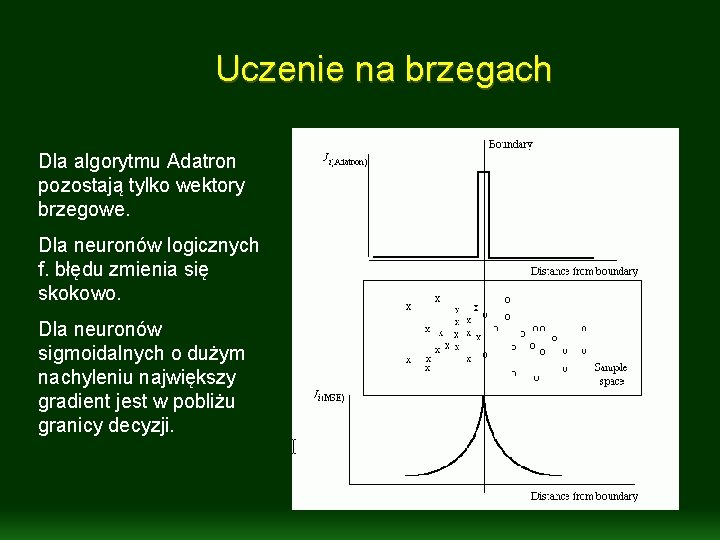
Uczenie na brzegach Dla algorytmu Adatron pozostają tylko wektory brzegowe. Dla neuronów logicznych f. błędu zmienia się skokowo. Dla neuronów sigmoidalnych o dużym nachyleniu największy gradient jest w pobliżu granicy decyzji.

Co dalej? • Perceptrony wielowarstwowe • Samoorganizacja • Sieci Hopfielda • Perceptrony wielowarstwowe • Sieci Hebbowskie i modele mózgu

Koniec wykładu 10