Perceptrons Slides adapted from Yaser AbuMostafa and Mohamed

Perceptrons Slides adapted from Yaser Abu-Mostafa and Mohamed Batouche

Roadmap • Covered two models – K-NN Classification • All features matter – Decision Tree Classification • Some features matter • Today… – Features matter to varying degrees • Linear methods (lines, planes, and hyperplanes) – Benefits • Simple algorithms • (Human) interpretable model parameters – Drawbacks • Most real-world problems are not linear 2

Creditworthiness • Banks would like to decide whether or not to extend credit to new customers – Good customers pay back loans – Bad customers default • Problem: Predict creditworthiness based on: – Salary, Years in residence, Current debt, Age, etc. 3

Perceptron • For a customer, – Approve credit if – Deny credit if • This linear formula can be written as: 4

Perceptron (cont’d) • Introduce an artificial coordinate x 0 = 1 – Called the bias term • So, perceptron implements: 5

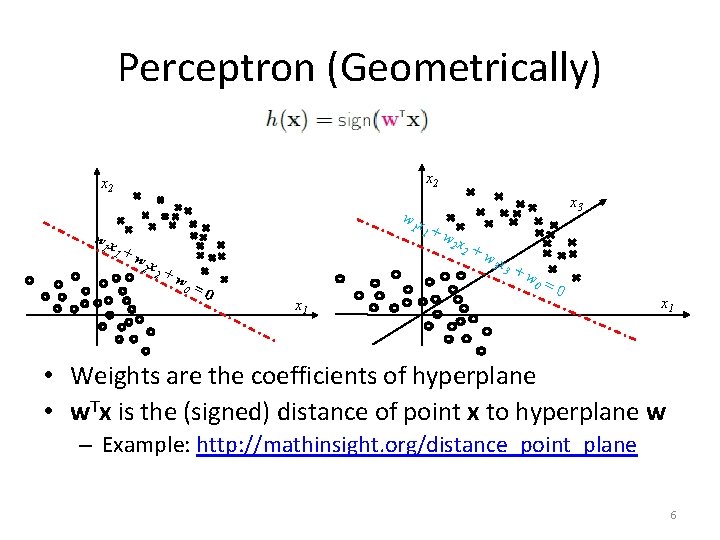
Perceptron (Geometrically) x 2 wx 1 1 wx 1 +w 2 x 2 +w 0 =0 1 x 3 +w 2 x 2 +w 3 x 3 +w 0 x 1 =0 x 1 • Weights are the coefficients of hyperplane • w. Tx is the (signed) distance of point x to hyperplane w – Example: http: //mathinsight. org/distance_point_plane 6

Perceptron Learning Algorithm (PLA) Example: https: //www. youtube. com/watch? v=v. Gwem. Zh. Pls. A This +1/-1 label trick is useful. We’ll see it again. 7

PLA Summary • One iteration of PLA updates the weights, w, for a misclassified point • Done when there are no misclassified points • Guaranteed to converge if data is linearly separable – What if the data is not linearly separable? 8

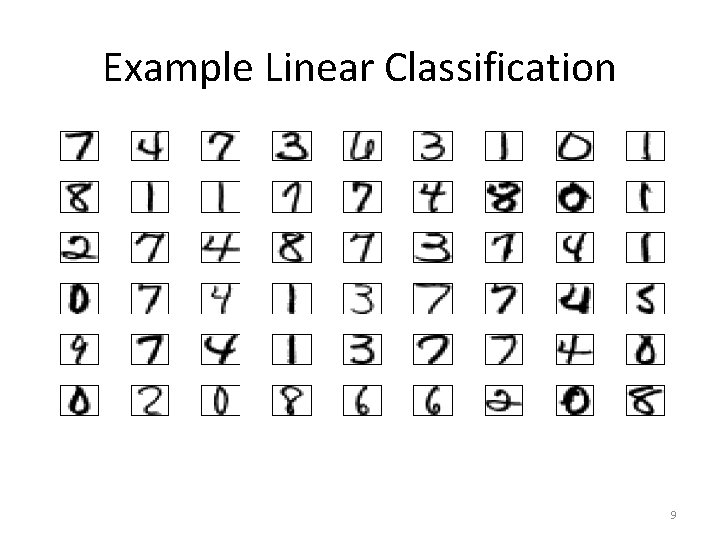
Example Linear Classification 9

Input Representation • Raw input: 16*16 image = 256 pixels x = (x 0, x 1, x 2, …, x 256) • Linear model: w = (w 0, w 1, w 2, …, w 256) • Features: Extract useful information from raw data – Intensity and symmetry x = (x 0, x 1, x 2) – Linear model w = (w 0, w 1, w 2) 10

Feature Space • Consider a binary classification task – “Is x a ‘ 1’ (positive) or a ‘ 5’ (negative)? ” Not linearly separable 11

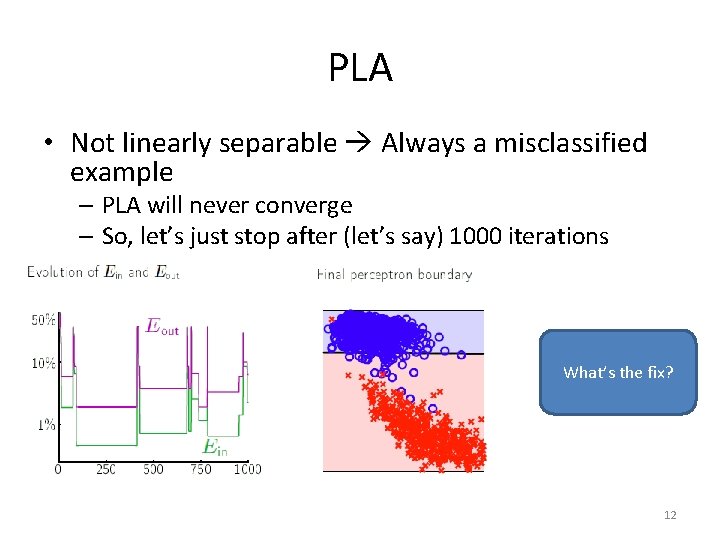
PLA • Not linearly separable Always a misclassified example – PLA will never converge – So, let’s just stop after (let’s say) 1000 iterations What’s the fix? 12

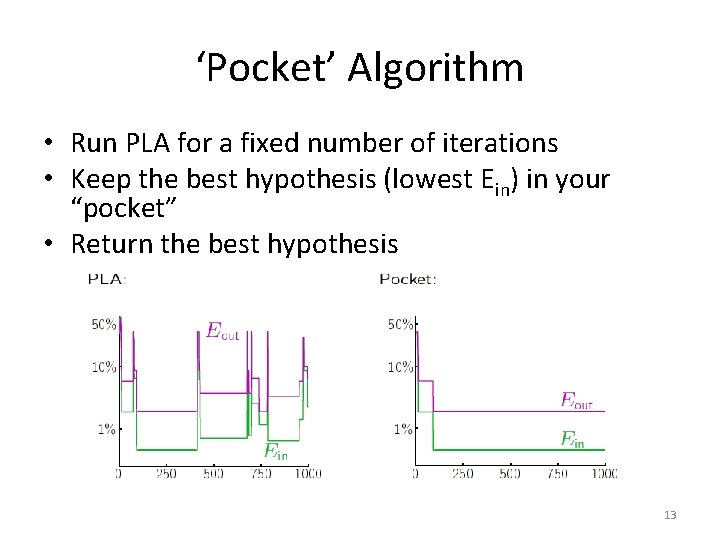
‘Pocket’ Algorithm • Run PLA for a fixed number of iterations • Keep the best hypothesis (lowest Ein) in your “pocket” • Return the best hypothesis 13

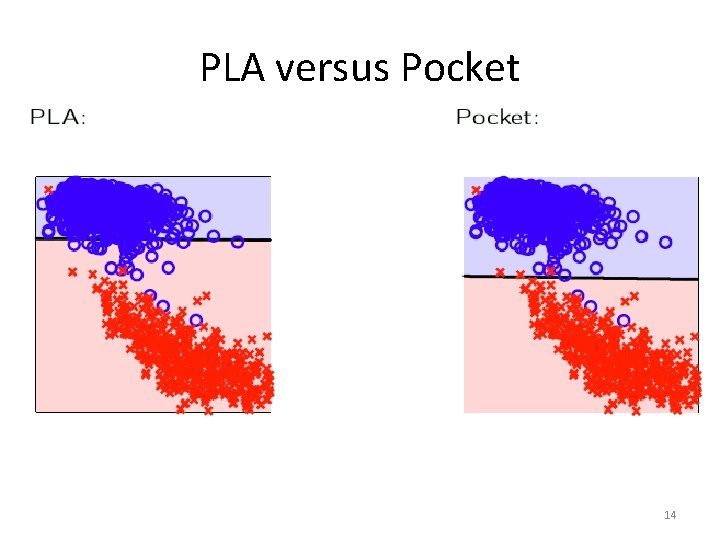
PLA versus Pocket 14

Linear Regression • Classification: Credit approval (yes / no) • Regression: Credit line (dollar amount) • Same input, x = • Linear regression output: 15

Training Data • Credit officers decide on credit lines: Credit line for the corresponding customer • Linear regression attempts to replicate this 16

Error Measure • Classification error (right or wrong) won’t work here – With regression, you can be “close” or “far” • How well does h(x) = w. Tx approximate f(x)? • We use squared error: (h(x) – f(x))2 17

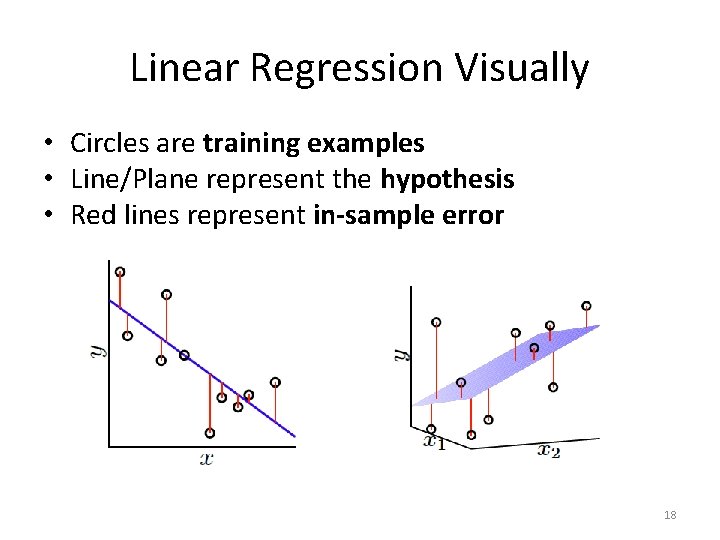
Linear Regression Visually • Circles are training examples • Line/Plane represent the hypothesis • Red lines represent in-sample error 18

Training (In-Sample) Error, Ein 19

Minimizing Ein 20

Linear Regression Algorithm 21

Linear Regression for Classification • Linear regression learns a real-valued function y = f(x) • Binary-valued functions are also real-valued: {+1, -1} • Use linear regression to get w where • sign(w. TXn) is likely to agree with • These are good initial weights for PLA / Pocket 22

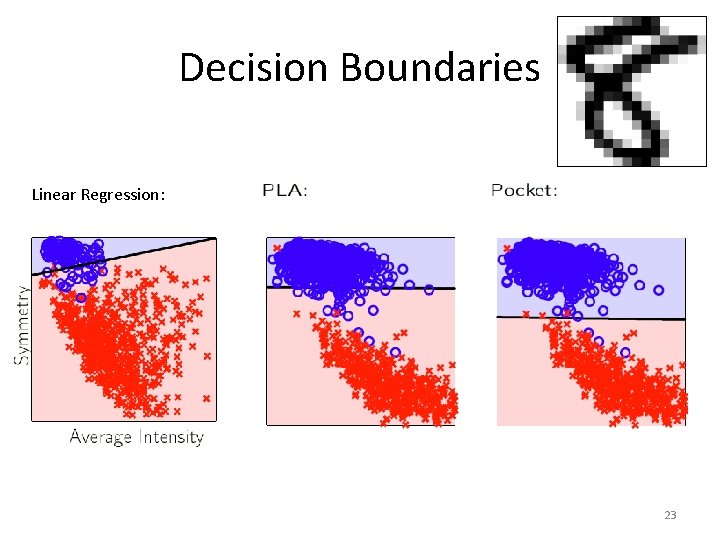
Decision Boundaries Linear Regression: 23

Recap • Linear methods – Lines, planes, hyperplanes – classification (PLA, Pocket Algorithm) – regression (pseudo-inverse) • Benefits of linear approaches – Simple algorithms – (Human) interpretable model parameters • Drawbacks – Most real-world problems are not linear 24

Back to Credit Example • Credit line is affected by ‘years in residence’ – But perhaps not linearly • Perhaps credit officers use a different model – Is ‘years in residence’ less than 1? – Is ‘years in residence’ greater than 5? • Can we do that with linear models? 25

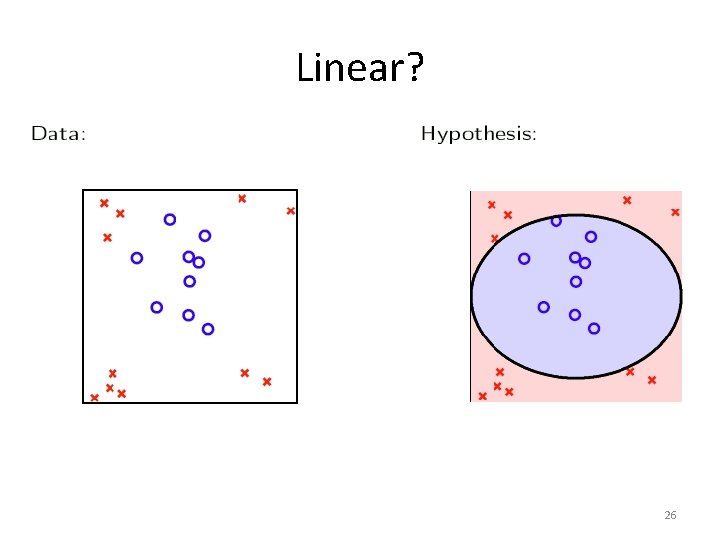
Linear? 26

Linear in what? • Linear regression implements: • Linear classification implements: • What are the unknowns? • Algorithms work because of linearity in the weights 27

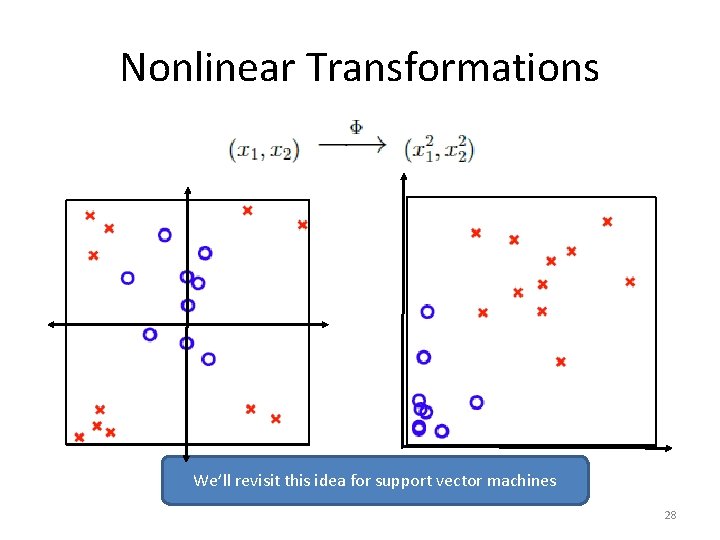
Nonlinear Transformations We’ll revisit this idea for support vector machines 28

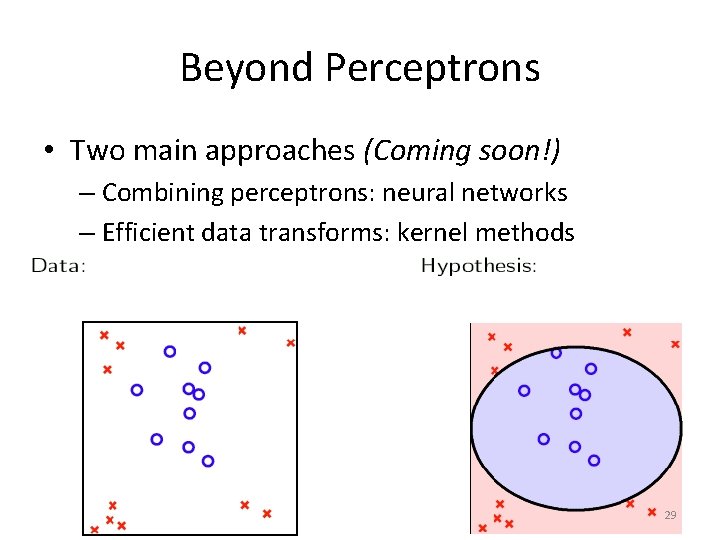
Beyond Perceptrons • Two main approaches (Coming soon!) – Combining perceptrons: neural networks – Efficient data transforms: kernel methods 29

Summary Credit Analysis • Benefits of linear approaches – Simple algorithms – (Human) interpretable model parameters • Drawbacks – Most real-world problems are not linear • Nonlinear transformations can help 30