Percents Understanding Percents A percent shows a part




























- Slides: 28

Percents

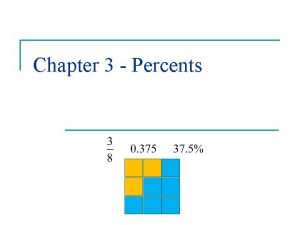
Understanding Percents A percent shows a part of a whole. v Remember • Fractions: the denominator tells how many parts a whole is divided into. (Any whole number except for zero can be a denominator. ) • Decimals: a whole is divided into tenths, hundredths, thousandths, & so on. v Percent: the whole is always divided into 100 parts. The word percent means “by the hundred or per one hundred. ” • Percent is shown with the sign %.

Example v Answer each question 1. The Rodriguez family has paid off 75% of their mortgage. What percent of the mortgage do they still have to pay? 2. Serena makes four times what she made when she first got out of school. Her income now is what percent of her income when she first left school?

Group Work v Answer 1. 2. each question. One evening during a flu epidemic, 30% of Marla’s students were absent from her exercise class. What percent of the students came to class? The current population of Eastport is three times what it was in 1960. The population now is what percent of the 1960 population?

Decimals to Percents v To change a decimal to a percent, move the decimal point two places to the right and write the percent sign (%). • If the decimal point moves to the end of the number, it is not necessary to write it. • You may have to add zeros.

Example v Write each decimal as a percent 1. 0. 32 2. 0. 005 3. 0. 125

Group Work v Write each decimal as a percent 1. 0. 09 2. 0. 0375 3. 0. 2

Percents to Decimals v To change a percent to a decimal, drop the percent sign (%) and move the decimal point two places to the left. v You may have to add zeros.

Example v Write each percent as a decimal. 1. 62 ½% 2. 7% 3. 200%

Group Work v Write each percent as a decimal. 1. 6 2/ 3% 2. 1. 5% 3. 8%

Fractions to Percents v There are two ways to change a fraction to a percent: • Method 1: Multiply fraction by 100% • Method 2: Divide the denominator of the fraction into the numerator and move the point two places to the right.

Example v Write 1 2 3 4 25 1 6 3 7 each fraction as a percent.

Group Work v Write 1 2 3 3 10 4 5 1 8 each fraction as a percent.

Percents to Fractions v To change a percent to a fraction, write the percent as a fraction with 100 as the denominator and reduce.

Example v Write each percent as a common fraction. 1. 8 1/ 3% 2. 4% 3. 80%

Group Work v Write each percent as a common fraction. 1. 66 2/3% 2. 12% 3. 90%

Identifying the Percent, the Whole, and the Part & Finding the Part v In a percent problem the percent is easy to identify. It has the % sign. v The word of suggests multiplication. The word that follows of is usually the whole. v The verb is suggests the = sign. The product of multiplying the percent times the whole is the part. • v percent x whole = part To multiply by a percent, first change the percent to a decimal or a fraction.

Example v Identify the percent, part, and whole for each of the following: 1. 8% of 753 is 13. 554 2. 50% of 88 is 44 v Solve. 1. 75% of 48 = 2. 1. 2% of 800 =

Group Work Identify the percent, part, and whole for each of the following: 1. 12 is 25% of 48 2. On a test with 20 problems, Maxim got 75% right. He got 15 problems right. v Solve. 1. 12. 5% of 56 = 2. Mr. and Mrs. Caruso make $32, 500 a year. They put 12% of their income into a retirement plan. How much do they put in their retirement plan in a year? v

Using Proportion to Find the Part v There is not single way to solve percent problems. When using this method you do not need to change the percent to a decimal. The proportions method: Part Whole = % 100

Example v Solve. 1. 6% of 250 = 2. 75% of 84 = 3. 12 is what percent of 48? 4. What percent of 32 is 16? 5. 60% of what number is 27?

Group Work v Solve. 1. 60% of 380 = 2. 15% of 7, 000 = 3. 14 is what percent of 21? 4. What percent of 45 is 36? 5. 12 ½% of what number is 8?

Multi-Step Problems v In some percent problems, you have to use two operations to find an answer. v First v Then find a percent of a number. add or subtract this new amount with the original amount in the problem.

Example v Read each problem carefully to decide if you need to add or subtract. 1. Selma makes $560 a week. Her employer takes out 15% of her pay for taxes and Social Security. How much does Selma take home each week? 2. Frank took a math test with 40 problems. He got 85% of the problems right. How many problems did he get wrong?

Group Work v Read each problem carefully to decide if you need to add or subtract. 1. Don bought tapes for $15. 60. The sales tax in his state is 5%. How much did the tapes cost including sales tax? 2. In June Petra’s phone bill was $24. 50. In July her bill was 30% more because of long distance calls. How much was her July phone bill?

Interest v Interest is money someone pays for using someone else’s money. A bank pays you interest for using your money in a savings account. You pay a bank interest for using the bank’s money on a loan. v To find interest, multiply the principal by the rate by the time. • The principal is the money you borrow or save. • The rate is the percent of the interest • The time is the number of years

Example v Find the interest for each of the following. 1. $800 at 6% annual interest for one year. 2. $360 at 3. 5% annual interest for 1 year 4 months

Group Work v Find the interest for each of the following. 1. $600 at 3. 5% annual interest for one year. 2. $450 at 4. 8% annual interest for one year. 3. $2, 400 at 10% annual interest for 1 year 8 months. 4. $3, 600 at 9% annual interest for 1 year 9 months
 How to calculate valid percent
How to calculate valid percent When god shows up he shows off
When god shows up he shows off Element of percent part of the whole
Element of percent part of the whole Waitress gets $4 000 tip
Waitress gets $4 000 tip The diagram shows part of a regular polygon
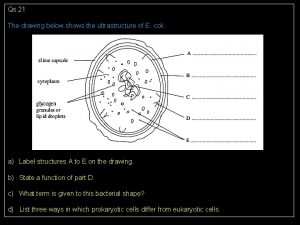
The diagram shows part of a regular polygon The diagram shows part of a prokaryotic cell
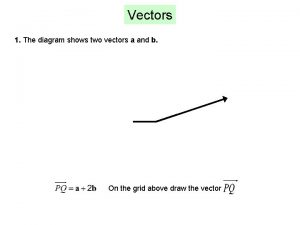
The diagram shows part of a prokaryotic cell The diagram below shows vector v
The diagram below shows vector v Examples of analogies
Examples of analogies Converting between percents decimals and fractions
Converting between percents decimals and fractions Converting between percents decimals and fractions
Converting between percents decimals and fractions Lesson 3 percents and decimals
Lesson 3 percents and decimals Percents to decimals
Percents to decimals Estimating percents
Estimating percents What
What Percents greater than 100 and less than 1
Percents greater than 100 and less than 1 Two sevenths as a percentage
Two sevenths as a percentage Percents to decimals
Percents to decimals Fractions decimals and percents calculator
Fractions decimals and percents calculator 6-2 relate fractions decimals and percents
6-2 relate fractions decimals and percents Reteaching 9-1 review percents and probability
Reteaching 9-1 review percents and probability Lesson 6-2 fractions, decimals, and percents answers
Lesson 6-2 fractions, decimals, and percents answers Estimating with percents
Estimating with percents Perbandingan desimal
Perbandingan desimal Hard order of operations problems
Hard order of operations problems Percent means
Percent means Part part whole addition
Part part whole addition Different parts of bar
Different parts of bar Unit ratio definition
Unit ratio definition Brainpop ratios
Brainpop ratios