Percents Definition A percent is another way of




















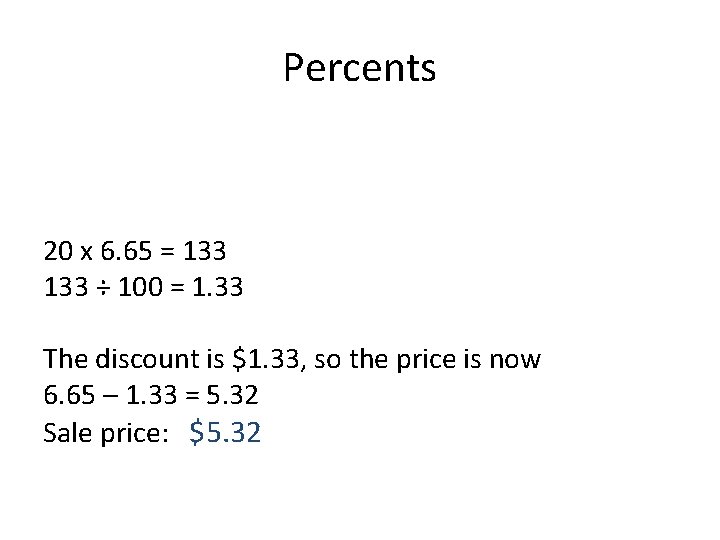







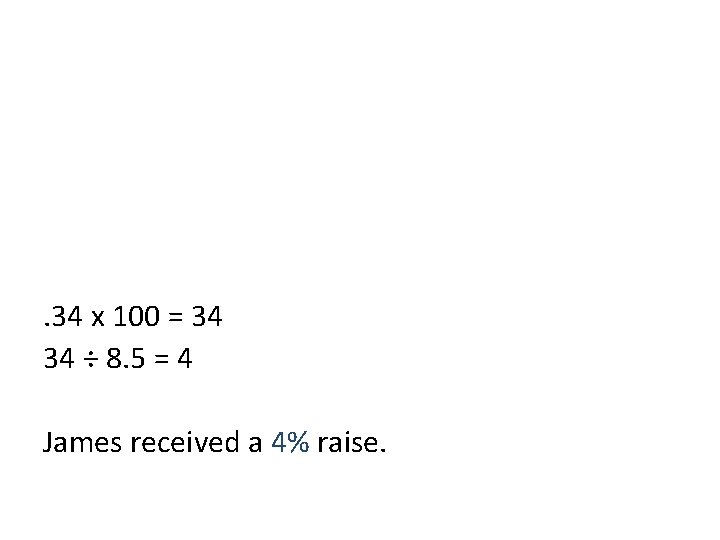



- Slides: 33

Percents Definition: A percent is another way of showing a fraction whose denominator is 100. Percent means parts per hundred. The word percent comes from the Latin phrase per centum, which means each | hundred. In mathematics, we use the symbol % for percent.

Percents Population of China: 1, 321, 851, 888 (July 2007 est. ) ------ out of -----Population of the world: 6, 602, 224, 175 It’s hard to grasp the relationship when China’s population is written as a fraction of world population. But turn it into a percent…. Almost exactly 20% Just about 20 out of every one hundred people in the world lives in China.

Percents • This proportion is the key to solving percent problems. You should memorize it.

Percents
• Let’s say that 4 out of 16 people in this class absolutely love math. We could represent that as a ratio 4 to 16 or . If we want to know what percentage of people surveyed love math, we look for an equivalent fraction with a denominator of 100.

• To solve any basic percent problem we use the same steps: 1. Write two fractions bars with = between, and write 100 as the second fraction’s denominator 2. Fill in the information we have according to the model.

3. Multiply along the diagonal whatever direction we have two numbers (not the ? ) In this case – 4 x 100 = 400 4. Divide the answer from step 4 by the remaining number (in this case 16) 400/16 = 25

Percents • GED percent problems will give you two out of the 3 necessary pieces of information. (Note that the 100 on the bottom right doesn’t change)

Example 1 – Finding the part • What is 20% of 300? • Step 1 – • Step 2 – we know the percent and the total. We’re trying to find the part, so

Example 1 – Finding the part • Step 4 – – Cross multiply 20 x 300 = 6000 • Step 5 – – divide by the remaining number 6000/100 = 60 20% of 300 is 60

Example 2 – Finding the total • 18 is 15% of what number? • Step 1 – • Step 2 – we know the part and the percent. We’re trying to find the total, so

Example 2 – Finding the total • Step 4 – – Cross multiply 18 x 100 = 1800 • Step 5 – – divide by the remaining number 1800/15= 120 15% of 120 is 18

Example 3 – Finding the percent • 70 is what percent of 800? • Step 1 – • Step 2 – we know the part and the total. We’re trying to find the percent, so

Example 3 – Finding the percent • Step 3– – Cross multiply 70 x 100 = 7000 • Step 4 – – divide by the remaining number 7000/800 = 8. 75 70 is 8. 75% of 800

You try: • 50 is what percent of 250? • What is 30% of 500? • 18 is 6% of what number? (press pause)

You try: • 50 is what percent of 250? (50 x 100)/250 = 20 • What is 30% of 500? (30 x 500)/100 = 150 • 18 is 6% of what number? (18 x 100)/6 = 300

Percents • Some problems using percents are a little more complicated. – Markup – Discount – Tax – Percent Change

Percents Mark-up Fred Meyer buys potted palms from a local grower for $3. 50 each. They sell them to the public at a 90% markup What is 90% markup? 90 x 3. 50 = 315 ÷ 100 = 3. 15

Percents • Mark-up Fred Meyer buys potted palms from a local grower for $3. 50 each. They sell them to the public at a 90% markup • Markup is $3. 15 – this is added to the original cost of the plant to reach the sale price. • $3. 50 + $3. 15 = $6. 65

Percents • Discount – Fred Meyer is having a 20% off sale on potted palms. How much are the plants now? • They are selling for $6. 65 • We need to find 20% of $6. 65

Percents • Discount – Fred Meyer is having a 20% off sale on potted palms. How much are the plants now? • They are selling for $6. 65 • We need to find 20% of $6. 65
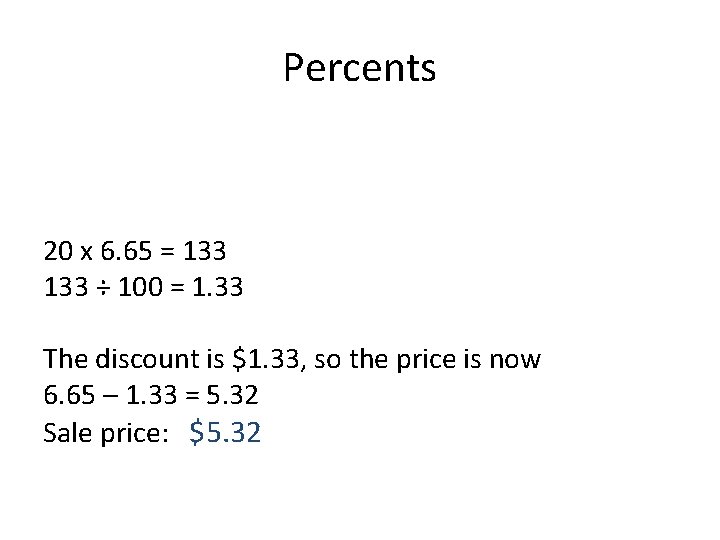
Percents 20 x 6. 65 = 133 ÷ 100 = 1. 33 The discount is $1. 33, so the price is now 6. 65 – 1. 33 = 5. 32 Sale price: $5. 32

Percents • Tax – If Washington State sales tax is 7% and you buy a potted palm at the sale price, how much will you pay at the register?

Percents • Tax – If Washington State sales tax is 7% and you buy a potted palm at the sale price, how much will you pay at the register? • We need to find 7% of 5. 32

Percents 7 x 5. 32 = 37. 24 ÷ 100 =. 3724 (since we’re talking about money we round to the nearest cent -. 37)

Percents • The price of the plant was $5. 32 and the tax is 37¢, so we need to add the tax to the price to get the final total: • 5. 32 +. 37 = 5. 69 • The total price at the register is $5. 69

Percents • Percent Change Problems – amount of change becomes part, original becomes total.

Percents • % Increase • James used to make $8. 50/hr. His boss gave him a raise, and now he makes $8. 84/hr. What percent raise did James get?

Percents • Percent Increase • James used to make $8. 50/hr. His boss gave him a raise, and now he makes $8. 84/hr. What percent raise did James get? • The original was 8. 50, and the amount it changed by is 8. 84 – 8. 50 =. 34
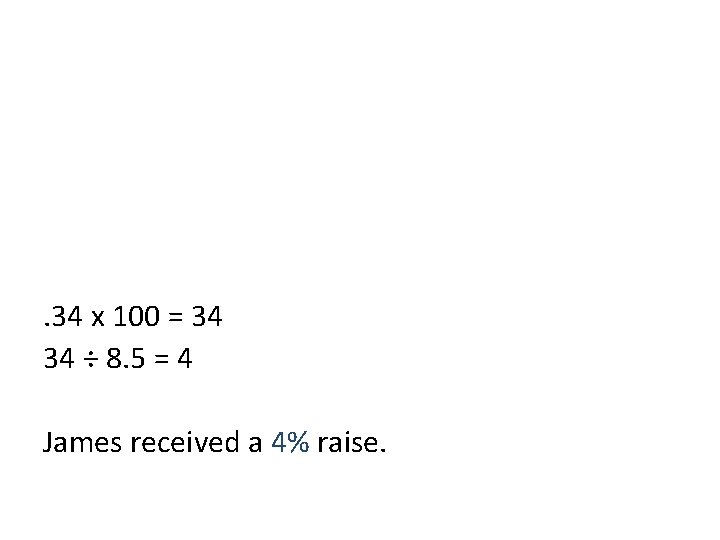
. 34 x 100 = 34 34 ÷ 8. 5 = 4 James received a 4% raise.

Percents • Percent Decrease • A cookbook was reduced from $20 to $15. What percent off was the book?

Percents 5 x 100 = 500 ÷ 20 = 25 The book was 25% off – The price had been decreased by 25%

Percents • Try the practice on pages 130 – 133 of the book. • Do GED Practice pages 15 – 17 and submit your answers using the answer sheet on BB.