Percentiles and BoxandWhisker Plots Percentiles Percentiles are numbers

Percentiles and Box-and-Whisker Plots

Percentiles • Percentiles are numbers based on 100 0 50 Median 100 • Median is a percentile – 50 th Percentile • SAT scores and class rank are measured in percentile

Why Percentiles and Box-and-Whisker Plots? • Data distributions are heavily skewed • Relative Position rather than exact values • Percentiles – Indicates the relative position of the scores • Visual summary of the data

Percentiles • The percentile of a distribution is a value such that P% of the data fall below. – i. e. . : When a score is in the 80 th percentile, this means that 80% of the scores fall below this number. – This does not mean that being in the 80 th percentile is the same as scoring an 80%!!

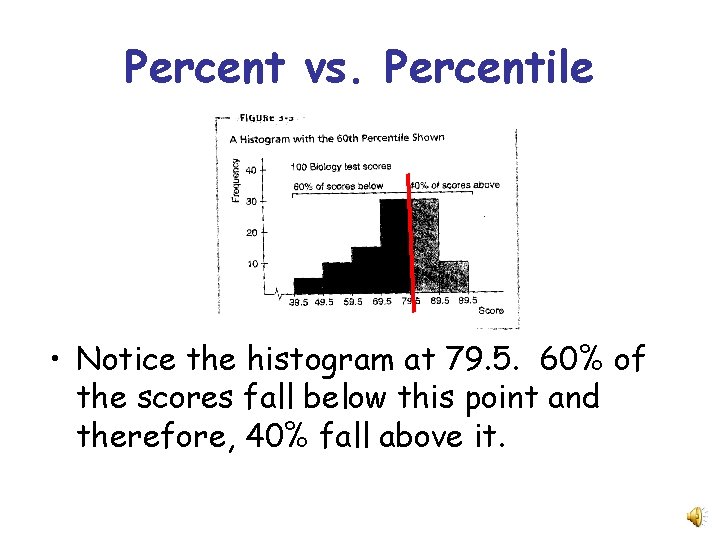
Percent vs. Percentile • Notice the histogram at 79. 5. 60% of the scores fall below this point and therefore, 40% fall above it.

Percent vs. Percentile • If scores range from 1 to 100 and your raw score is 95, does this necessarily mean that your score is in the 95 th percentile? – No—Percentile indicates the relative position of the scores. How many scores are below yours at 95? – If the test was easy, then there will be fewer scores below yours.

Determining Percentiles • Rank data from smallest to largest. • Divide the data into Quartiles. – Quartiles are percentiles that divide the data into fourths. – Q 1 = 25 th percentile – Q 2 = 50 th percentile (median) – Q 3 = 75 th percentile 0 25 Q 1 50 Q 2 75 Q 3 100

Interquartile Range (IQR) • Measures the spread of the data. • Describes the middle half of the data • IQR = Q 3 – Q 1 0 25 Q 1 50 75 Q 3 100

Five-Number Summary • • • Summarizes the data and its spread Lowest Value Q 1 Q 2 Median Q 3 Highest Value

Box-and-Whisker Plot • Visual image of the data spread • Based on the Five-Number Summary • Vertical scale to include the lowest and highest values • Draw a box from Q 1 to Q 3 • Draw a line for the median • Connect Q 1 to lowest value and Q 3 to highest

Box-and-Whisker Plot • Be Aware of: – Position of the median • Closer to the lower portion—lower values are more concentrated • Closer to the higher portion—higher values are more concentrated – Length of the whiskers • Longer lengths indicate skewness in that direction

Outliers • Exceptionally high or low values • Causes – Data collection errors – Data entry errors – Valid but unusual data • Identify outliers and determine if the values are in error • Detection – Lower Limit: Q 1 – 1. 5 X (IQR) – Upper Limit: Q 3 + 1. 5 X (IQR)

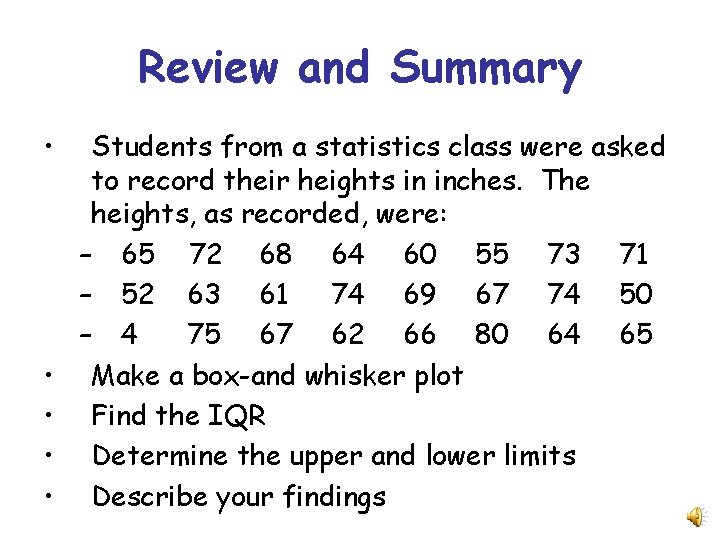
Review and Summary • • • Students from a statistics class were asked to record their heights in inches. The heights, as recorded, were: – 65 72 68 64 60 55 73 71 – 52 63 61 74 69 67 74 50 – 4 75 67 62 66 80 64 65 Make a box-and whisker plot Find the IQR Determine the upper and lower limits Describe your findings