PENYIMPANGAN BENTUK STANDAR METODE SIMPLEKS Juwairiah S Si

PENYIMPANGAN BENTUK STANDAR METODE SIMPLEKS Juwairiah, S. Si. , M. T Sistem Informasi UPN VEteran Yogyakarta

Penyimpangan Bentuk Standar Simplex Penyimpangan bentuk standar dapat terjadi karena : 1. Fungsi tujuan (Z) bukan Maximalisasi, tetapi Minimalisasi 2. Fungsi batasan bertanda (=) atau (≥) 3. Syarat X 1 atau X 2 tidak terpenuhi, misalkan X 1 ≥ - 10 (negatif)

Beberapa ketentuan dalam metode simpleks : • Nilai kanan (NK ) fungsi tujuan harus nol (0). • Nilai kanan (NK) fungsi kendala harus positif. Apabila negatif, nilai tersebut harus dikalikan – 1. • Untuk fungsi tujuan MIN agar menjadi MAX dikalikan dengan (-1) • Fungsi kendala dengan tanda “ ” harus diubah ke bentuk “=” dengan menambahkan variabel slack/surplus. Variabel slack/surplus disebut juga variabel dasar. • Fungsi kendala dengan tanda “=” harus ditambah artificial variable

• Jika kendala bertanda “>”, kurangkan ruas kiri dgn variabel surplus dan tambahkan juga ruas kiri dgn artificial variabel. • Masukkan / tambahkan pula variabel-variabel slack/surplus dan artificial ke dalam fungsi tujuan, dimana koefisien untuk var slack/surplus = 0 dan koefisien var artificial = M ( M adalah konstanta yang nilainya sangat besar sekali, tapi berhingga, misalnya ribuan, puluhan ribu, dst) • Sebelum masuk ke tabel simplex, koefisien artificial variable harus diubah menjadi nol (0) dengan cara mengurangi dengan baris kendala yang memuat variabel tersebut

CONTOH PENYIMPANGAN BENTUK STANDAR 1. Fungsi batasan dengan tanda sama dengan (=) Contoh : Fungsi tujuan: Maximumkan Z = 3 X 1 + 5 X 2 Fungsi kendala: 1) 2 X 1 8 2) 3 X 2 15 3) 6 X 1 + 5 X 2 = 30

Bentuk standar Simpleks : Fungsi kendala: 1) 2 X 1 8 => 2 X 1 +X 3 = 8 2) 3 X 2 15 => 3 X 2 +X 4 = 15 3) 6 X 1 + 5 X 2= 30=> 6 X 1 + 5 X 2+ X 5 = 30 X 3, X 4 = slack variable X 5 = artificial variable Fungsi tujuan: => Z – 3 X 1 – 5 X 2 + 0. X 3 +0. X 4 + MX 5 = 0

• Nilai setiap variabel dasar (X 5) harus sebesar 0, sehingga fungsi tujuan harus dikurangi dengan M dikalikan dengan baris fungsi kendala yang bersangkutan (3). Nilai baris Z sebagai berikut: [ -3 -5 0 M[6 5 0 (-6 M-3) (-5 M-5) 0 0 M , 0] 1 , 30] 0 -30 M

Tabel Simplex (awal) Var. D Z X 1 X 2 X 3 X 4 X 5 NK index Z 1 -6 M-3 -5 M-5 0 0 0 -30 M X 3 0 2 0 1 0 0 8 4 X 4 0 0 3 0 15 ~ X 5 0 6 5 0 0 1 30 5 sr
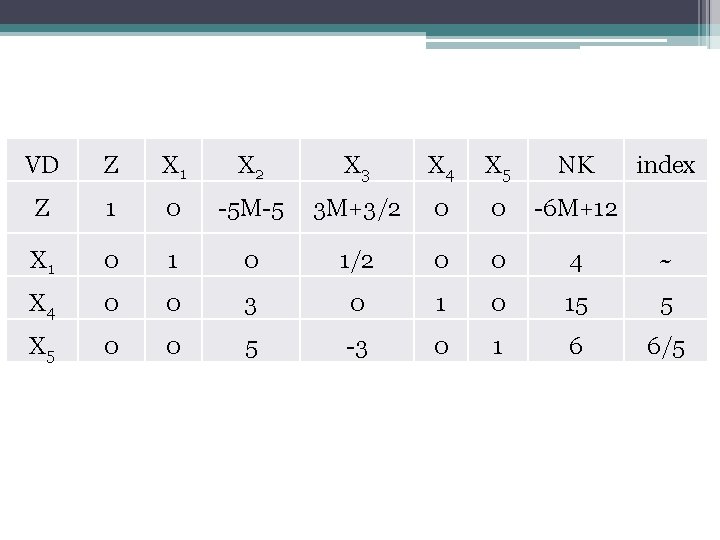
VD Z X 1 X 2 X 3 X 4 X 5 NK index Z 1 0 -5 M-5 3 M+3/2 0 0 -6 M+12 X 1 0 1/2 0 0 4 ~ X 4 0 0 3 0 15 5 X 5 0 0 5 -3 0 1 6 6/5
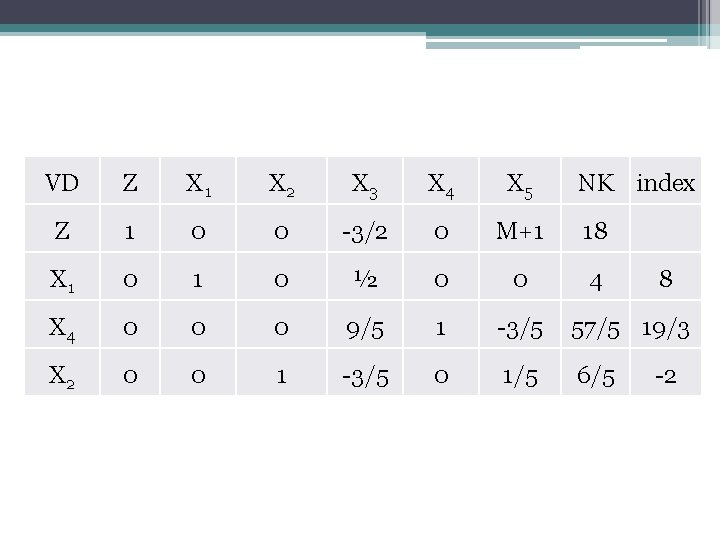
VD Z X 1 X 2 X 3 X 4 X 5 NK index Z 1 0 0 -3/2 0 M+1 18 X 1 0 ½ 0 0 4 X 4 0 0 0 9/5 1 -3/5 57/5 19/3 X 2 0 0 1 -3/5 0 1/5 6/5 8 -2
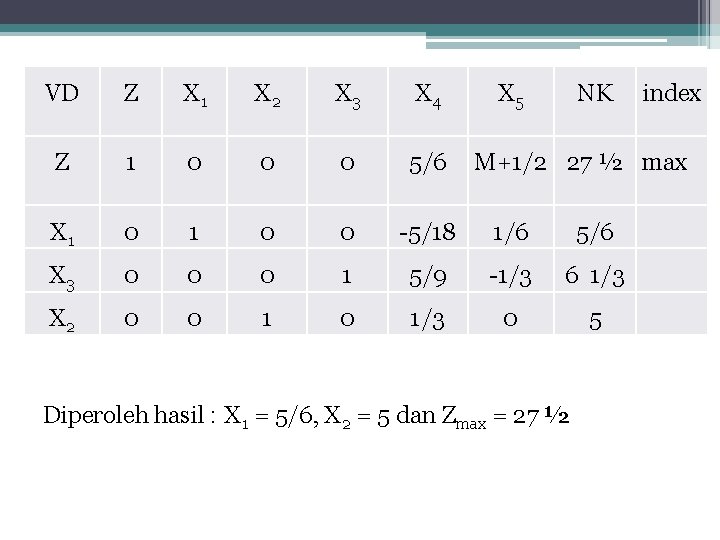
VD Z X 1 X 2 X 3 X 4 X 5 NK Z 1 0 0 0 5/6 X 1 0 0 -5/18 1/6 5/6 X 3 0 0 0 1 5/9 -1/3 6 1/3 X 2 0 0 1/3 0 5 index M+1/2 27 ½ max Diperoleh hasil : X 1 = 5/6, X 2 = 5 dan Zmax = 27 ½

2. Fungsi tujuan : Minimisasi • Soal minimisasi harus diubah menjadi maksimisasi dengan cara mengganti tanda positif dan negatif pada fungsi tujuan. Contoh: Fungsi Tujuan : Minimalkan Z = 3 X 1 + 5 X 2 Dengan batasan : Mesin A 2 X 1 =8 Mesin B 3 X 2 ≤ 15 Mesin C 6 X 1 + 5 X 2 ≥ 30 , dimana X 1 dan X 2 ≥ 0

Bentuk Standar Simpleks Fungsi Tujuan: Minimalkan Z = 3 X 1 + 5 X 2 menjadi Maksimalkan (-Z) = -3 X 1 – 5 X 2 Fungsi batasan/kendala: 2 X 1 = 8 2 X 1 + X 3 = 8 3 X 2 ≤ 15 3 X 2 + X 4 = 15 6 X 1 + 5 X 2 ≥ 30 6 X 1 + 5 X 2 -X 5 + X 6 = 30 X 4, X 5 = slack/surplus variable X 3, X 6 = artificial variable Sehingga fungsi tujuan menjadi : Maksimalkan : –Z + 3 X 1 + 5 X 2 + MX 3 +0. X 4+0. X 5+ MX 6 = 0

Masalah berikutnya yang muncul adalah setiap variabel dasar (slack atau artificial variabel), harus bernilai nol, sehingga MX 3 dan MX 6 di atas harus di-nol-kan terlebih dahulu, sebelum dipindah ke tabel simplex. Cara yang digunakan adalah dengan mengurangi bilangan M tersebut dengan bilangan M itu sendiri, yang sebelumnya dikalikan dengan setiap nilai batasan yang menyebabkan munculnya bilangan M tersebut.

Nilai fungsi tujuan terakhir adalah : 3 5 M 0 0 M 0 • Hilangkan M yang pertama terlebih dahulu. X 1 X 2 3 5 M( 2 0 X 3 M 1 X 4 0 0 X 5 0 0 X 6 M 0 3 -2 M 0 0 0 M 5 NK 0 fungsi tujuan 8 ) kendala (1) – -8 M

Selanjutnya kita hilangkan M yang kedua. • 3 -2 M 5 0 0 0 M -8 M ( 6 5 0 0 -1 1 30 ) x M _____________________3 -8 M 5 -5 M 0 0 M 0 -38 M, Atau -8 M+3 -5 M+5 0 0 M 0 -38 M Yang merupakan nilai dari fungsi tujuan yang baru selanjutnya akan dimasukkan ke tabel simplex, sehingga tabel simlex awalnya adalah sebagai berikut :
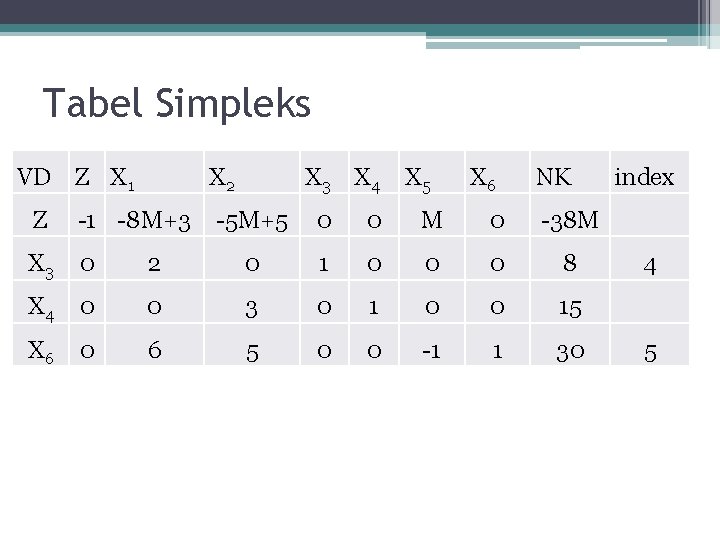
Tabel Simpleks VD Z X 1 X 2 Z -1 -8 M+3 X 3 0 X 4 X 6 X 3 X 4 X 5 X 6 NK -5 M+5 0 0 M 0 -38 M 2 0 1 0 0 0 8 0 0 3 0 1 0 0 15 0 6 5 0 0 -1 1 30 index 4 5
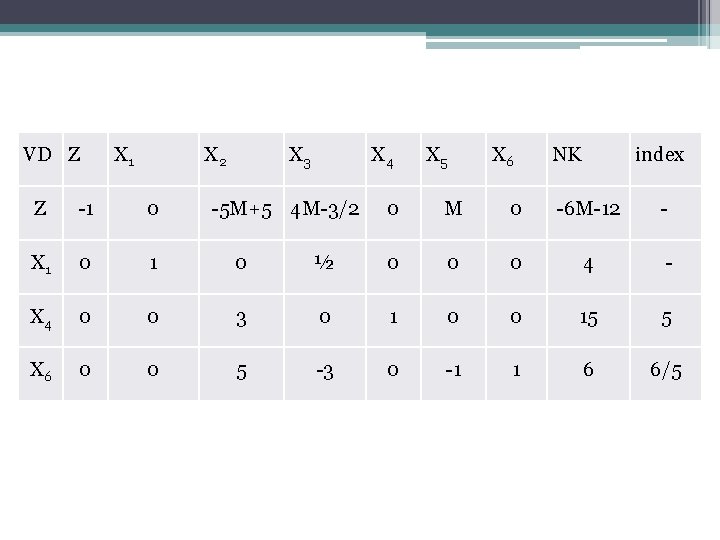
VD Z X 1 X 2 X 3 Z -1 0 X 4 0 0 X 6 0 0 X 4 -5 M+5 4 M-3/2 X 5 X 6 NK index 0 M 0 -6 M-12 - ½ 0 0 0 4 - 3 0 1 0 0 15 5 5 -3 0 -1 1 6 6/5
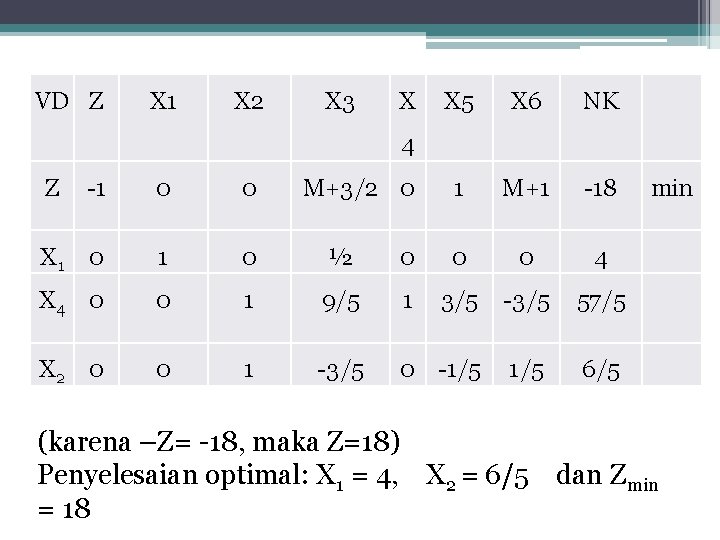
VD Z X 1 X 2 X 3 X X 5 X 6 NK 1 M+1 -18 4 Z -1 0 0 M+3/2 0 X 1 0 ½ 0 0 0 4 X 4 0 0 1 9/5 1 3/5 -3/5 57/5 X 2 0 0 1 -3/5 0 -1/5 6/5 min (karena –Z= -18, maka Z=18) Penyelesaian optimal: X 1 = 4, X 2 = 6/5 dan Zmin = 18
- Slides: 19