PENYAJIAN DATA 1 Tujuan Penyajian Data Memberi gambaran

PENYAJIAN DATA 1

Tujuan Penyajian Data • Memberi gambaran yang sistematis tentang peristiwa-peristiwa yang merupakan hasil penelitian atau observasi, • Data lebih cepat ditangkap dan dimengerti, • Memudahkan dalam membuat analisis data, dan 2

Cara Penyajian Data • Tabel • Gambar/Grafik 3

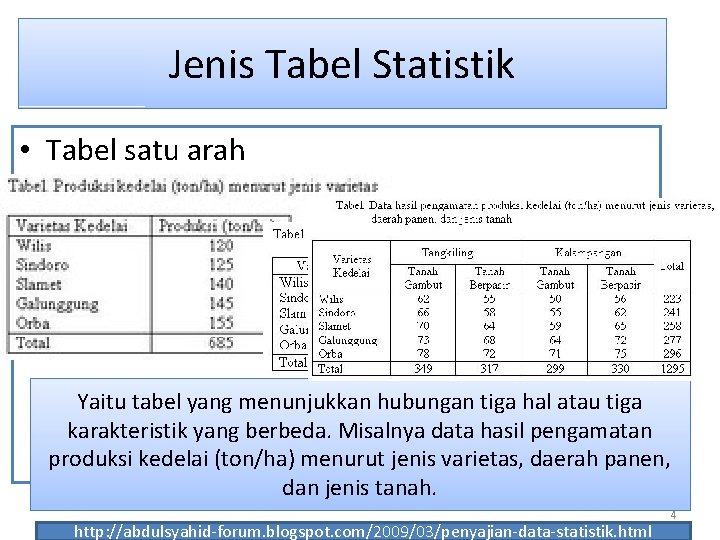
Jenis Tabel Statistik • Tabel satu arah • Tabel arah majemuk - Tabel dua arah - Tabel tiga arah Yaitu tabel yang menunjukkan hubungan tiga hal atau tiga Yaitu tabel yang menunjukkan hubungan duasatu hal atau dua Yaitu tabel yang memuat keterangan mengenai karakteristik yang berbeda. Misalnya data hasil pengamatan karakteristik yang Misalnya data Produksi kedelai satu karakteristik saja. berbeda. Misalnya datajenis Produksi kedelai menurut produksi kedelai (ton/ha) menurut varietas, daerah panen, jenis varietas dan daerah panen jenis varietasmenurut yang ditanam. dan jenis tanah. http: //abdulsyahid-forum. blogspot. com/2009/03/penyajian-data-statistik. html 4

Jenis Grafik/Gambar • • • Grafik garis (line chart), Grafik Batangan (bar chart), Grafik lingkaran (pie chart), Grafik gambar (Pictogram chart) Diagram Pencar (Scatter diagram) 5

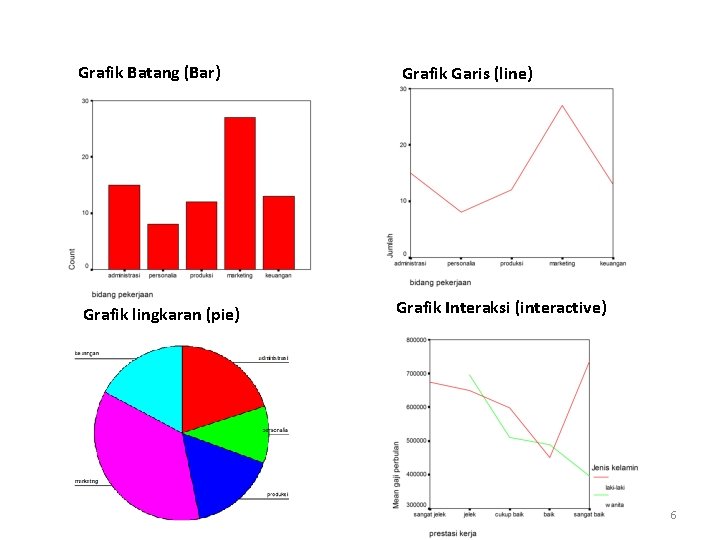
Grafik Batang (Bar) Grafik lingkaran (pie) Grafik Garis (line) Grafik Interaksi (interactive) 6

Grafik gambar 1: 10 7

DISTRIBUSI FREKUENSI 8

Distribusi Frekuensi • Bentuk pengelompokan data untuk menggambarkan distribusi data • Dapat dinyatakan dalam S bentuk tabel distribusi frekuensi S histogram atau poligon frekuensi 9

Prosedur Umum Penyusunan Tabel Dist Frekuensi • Tentukan banyaknya kelas • Tentukan lebar kelas • Hitung frekuensi untuk setiap kelas 10

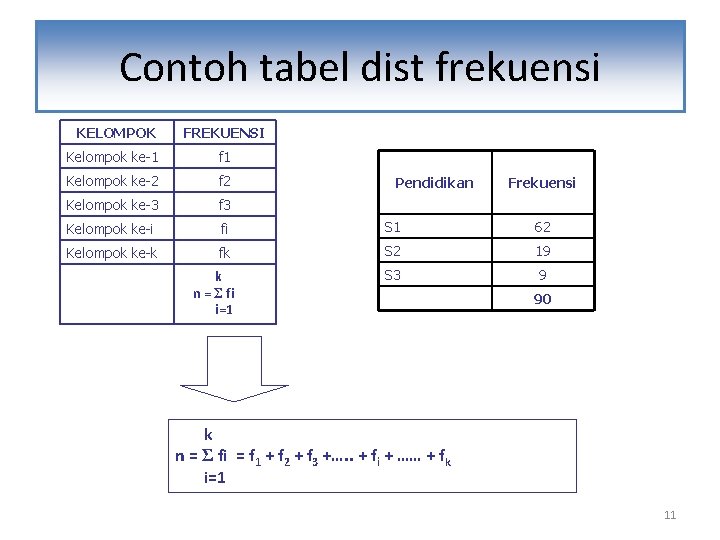
Contoh tabel dist frekuensi KELOMPOK FREKUENSI Kelompok ke-1 f 1 Kelompok ke-2 f 2 Kelompok ke-3 f 3 Kelompok ke-i fi S 1 62 Kelompok ke-k fk S 2 19 k n = Σ fi i=1 S 3 9 Pendidikan Frekuensi 90 k n = Σ fi = f 1 + f 2 + f 3 +…. . + fi + …… + fk i=1 11

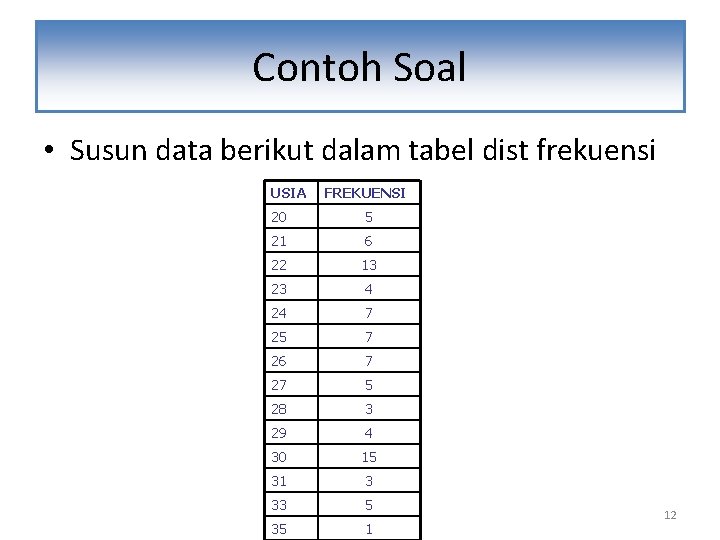
Contoh Soal • Susun data berikut dalam tabel dist frekuensi USIA FREKUENSI 20 5 21 6 22 13 23 4 24 7 25 7 26 7 27 5 28 3 29 4 30 15 31 3 33 5 35 1 12

Langkah-langkah • Tentukan rentang RENTANG: NILAI DATA TERBESAR – NILAI DATA TERKECIL • Tentukan banyak kelas (k) ATURAN STURGES: k = 1 + (3, 322)(log n) • Tentukan panjang kelas (p) p = RENTANG/k 13

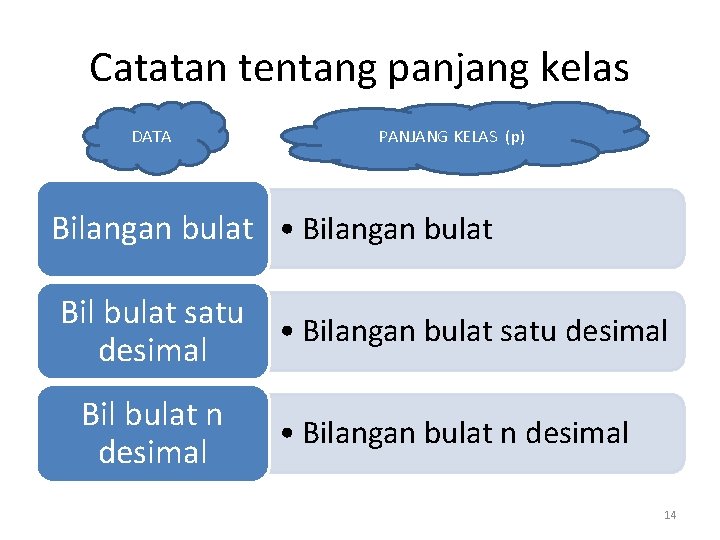
Catatan tentang panjang kelas DATA PANJANG KELAS (p) Bilangan bulat • Bilangan bulat Bil bulat satu • Bilangan bulat satu desimal Bil bulat n desimal • Bilangan bulat n desimal 14

Lanjutan langkah-langkah • Tentukan nilai ujung bawah kelas interval pertama Boleh mengambil nilai data terkecil atau nilai data yang lebih kecil dari nilai data terkecil • Masukkan semua data ke dalam interval kelas 15

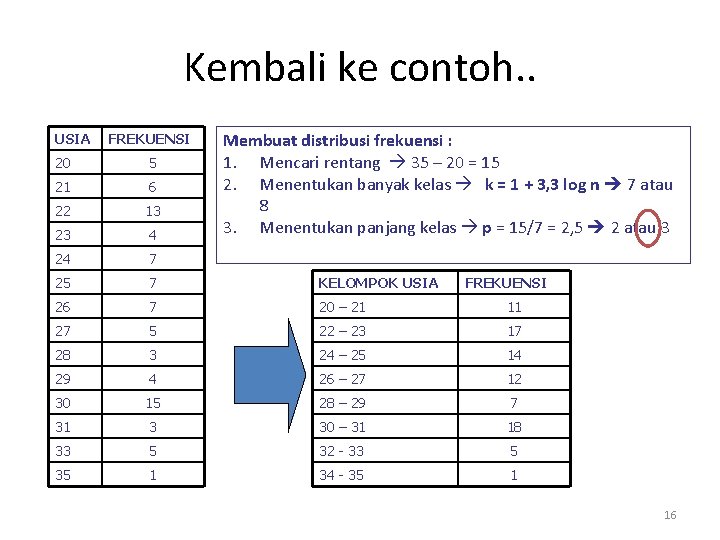
Kembali ke contoh. . USIA FREKUENSI Membuat distribusi frekuensi : 1. Mencari rentang 35 – 20 = 15 2. Menentukan banyak kelas k = 1 + 3, 3 log n 7 atau 8 3. Menentukan panjang kelas p = 15/7 = 2, 5 2 atau 3 20 5 21 6 22 13 23 4 24 7 25 7 KELOMPOK USIA 26 7 20 – 21 11 27 5 22 – 23 17 28 3 24 – 25 14 29 4 26 – 27 12 30 15 28 – 29 7 31 3 30 – 31 18 33 5 32 - 33 5 35 1 34 - 35 1 FREKUENSI 16

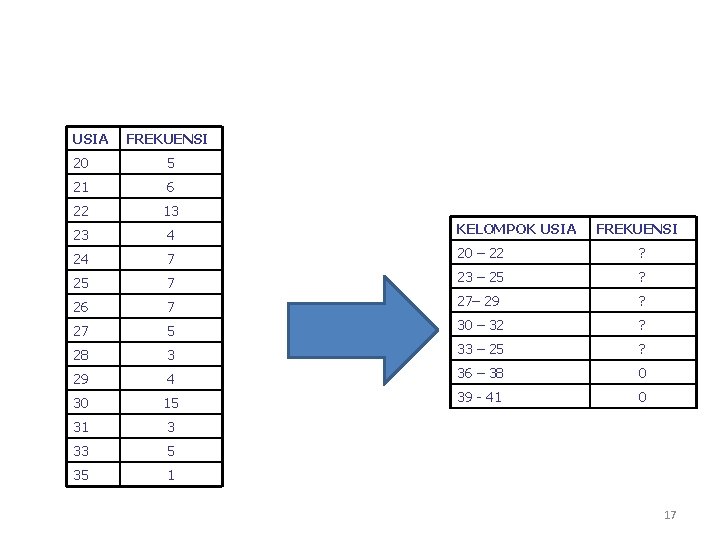
USIA FREKUENSI 20 5 21 6 22 13 23 4 KELOMPOK USIA 24 7 20 – 22 ? 25 7 23 – 25 ? 26 7 27– 29 ? 27 5 30 – 32 ? 28 3 33 – 25 ? 29 4 36 – 38 0 30 15 39 - 41 0 31 3 33 5 35 1 FREKUENSI 17

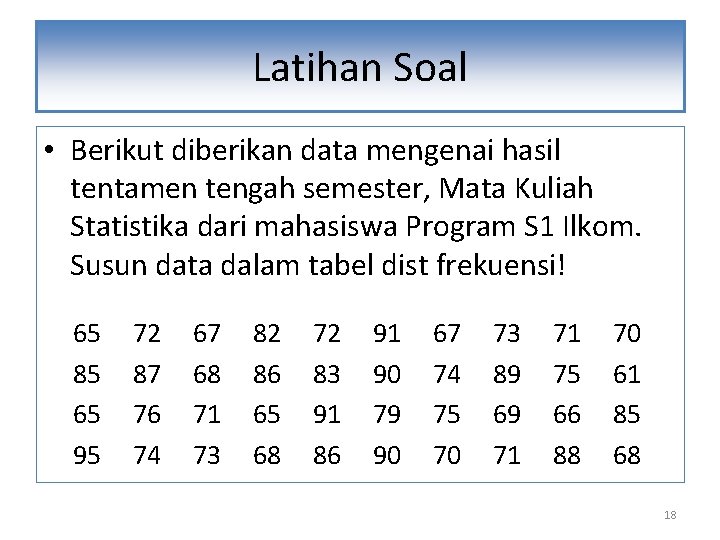
Latihan Soal • Berikut diberikan data mengenai hasil tentamen tengah semester, Mata Kuliah Statistika dari mahasiswa Program S 1 Ilkom. Susun data dalam tabel dist frekuensi! 65 85 65 95 72 87 76 74 67 68 71 73 82 86 65 68 72 83 91 86 91 90 79 90 67 74 75 70 73 89 69 71 71 75 66 88 70 61 85 68 18

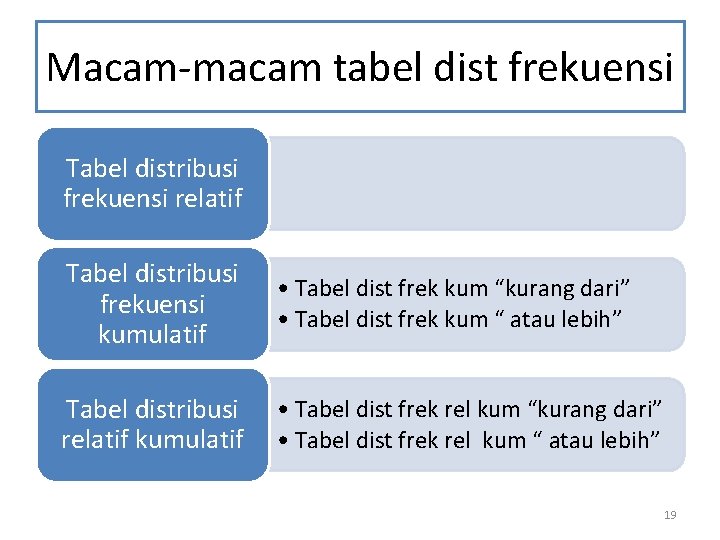
Macam-macam tabel dist frekuensi Tabel distribusi frekuensi relatif Tabel distribusi frekuensi kumulatif • Tabel dist frek kum “kurang dari” • Tabel dist frek kum “ atau lebih” Tabel distribusi relatif kumulatif • Tabel dist frek rel kum “kurang dari” • Tabel dist frek rel kum “ atau lebih” 19

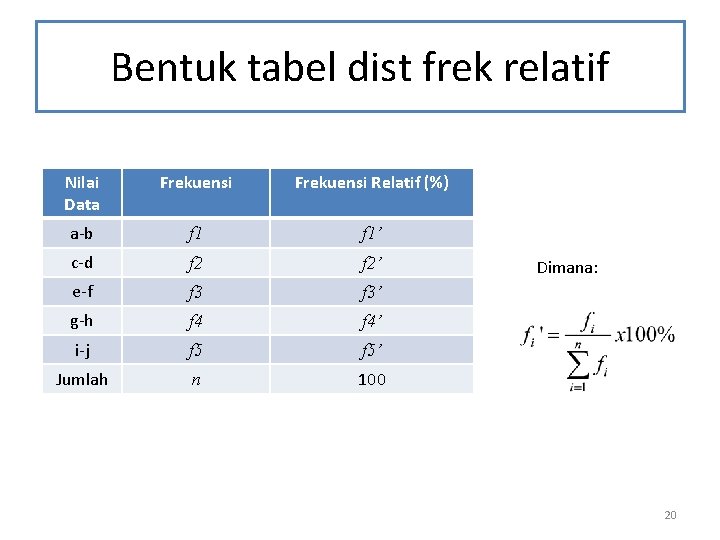
Bentuk tabel dist frek relatif Nilai Data Frekuensi Relatif (%) a-b f 1’ c-d f 2’ e-f f 3’ g-h f 4’ i-j f 5’ Jumlah n 100 Dimana: 20

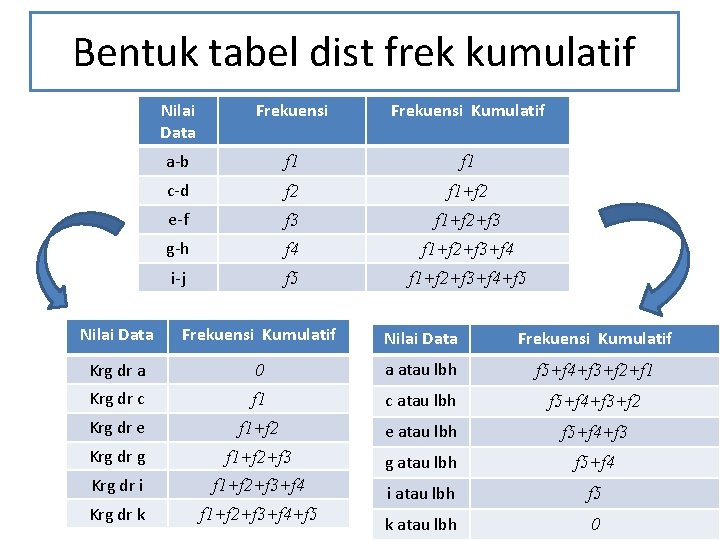
Bentuk tabel dist frek kumulatif Nilai Data Frekuensi Kumulatif a-b f 1 c-d f 2 f 1+f 2 e-f f 3 f 1+f 2+f 3 g-h f 4 f 1+f 2+f 3+f 4 i-j f 5 f 1+f 2+f 3+f 4+f 5 Nilai Data Frekuensi Kumulatif Krg dr a 0 a atau lbh f 5+f 4+f 3+f 2+f 1 Krg dr c f 1 c atau lbh f 5+f 4+f 3+f 2 Krg dr e f 1+f 2 e atau lbh f 5+f 4+f 3 Krg dr g f 1+f 2+f 3 g atau lbh f 5+f 4 Krg dr i f 1+f 2+f 3+f 4 Krg dr k i atau lbh f 5 f 1+f 2+f 3+f 4+f 5 k atau lbh 0 21

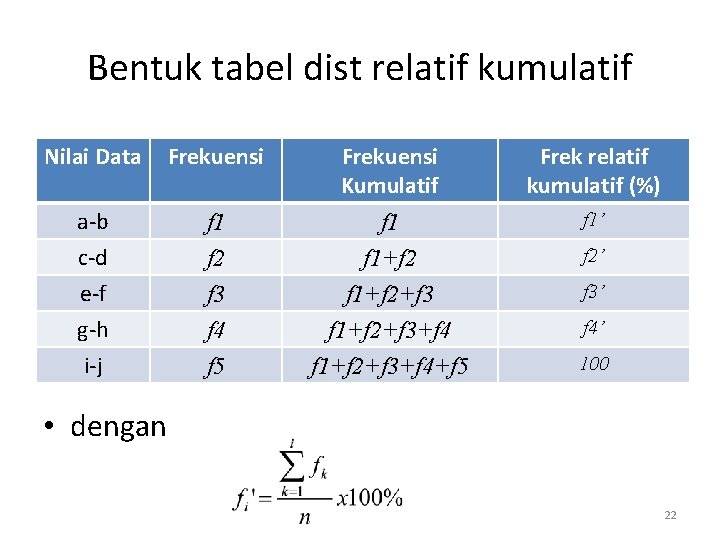
Bentuk tabel dist relatif kumulatif Nilai Data Frekuensi Kumulatif Frek relatif kumulatif (%) a-b c-d e-f g-h i-j f 1 f 2 f 3 f 4 f 5 f 1+f 2+f 3+f 4 f 1+f 2+f 3+f 4+f 5 f 1’ f 2’ f 3’ f 4’ 100 • dengan 22

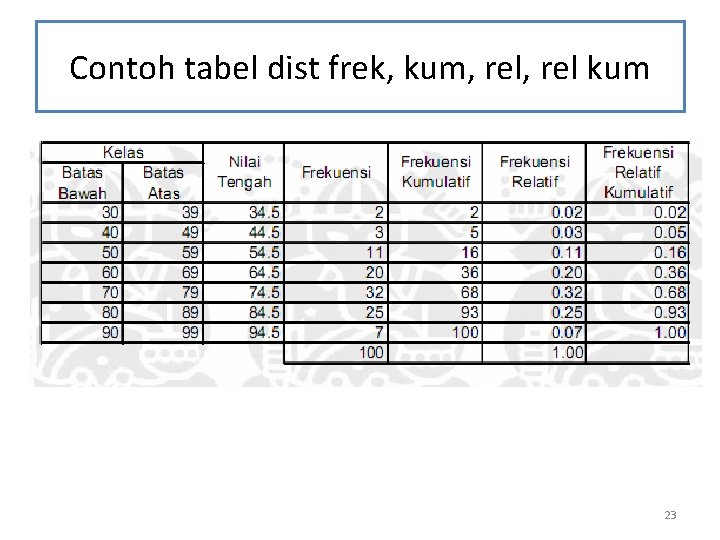
Contoh tabel dist frek, kum, rel kum 23

Macam-macam bentuk diagram • Data tidak terkelompok : diagram batang, diagram lingkaran, garis, gambar (simbol) • Data terkelompok : histogram dan poligon frekuensi, ogive 24

Histogram dan poligon frekuensi • Histogram mrpk bentuk diagram batng yg digunakan untuk menggambarkan dist frekuensi • Poligon (kurva) frekuensi mrpk bentuk diagram garis yg digunakan utk menggambarkan dist frekuensi 25

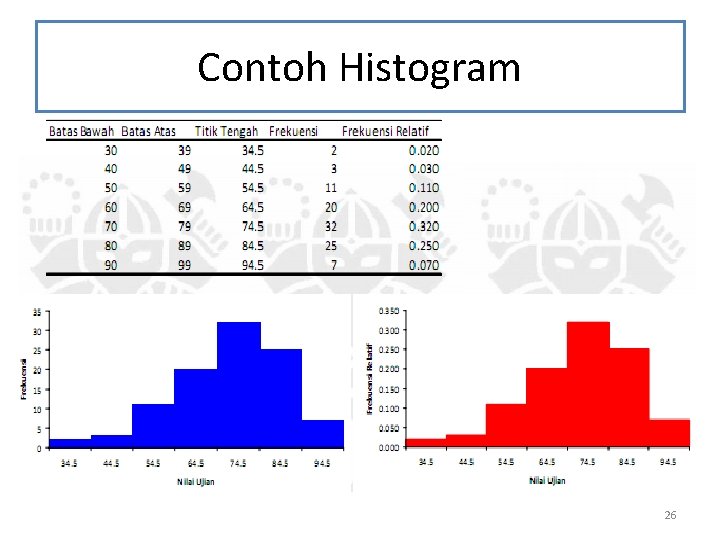
Contoh Histogram 26

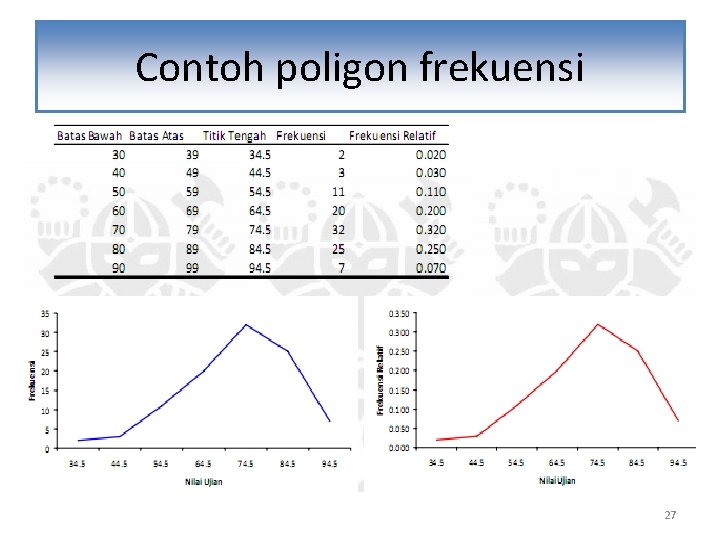
Contoh poligon frekuensi 27

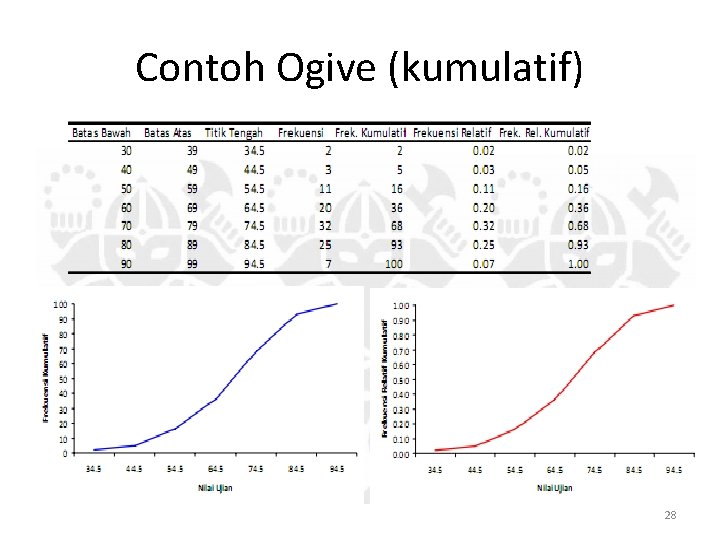
Contoh Ogive (kumulatif) 28

Catatan tentang batas dan bawah • Batas bawah (bb) = ujung bwh – ketelitian data yang digunakan • Batas (ba) = ujung atas + ketelitian data yg digunakan Data Ketelitian yang digunakan Bil bulat Bil satu desimal Bil dua desimal 0, 5 0, 005 dst 29

Catatan tentang titik tengah (tanda kelas) Titik tengah = ½ (ujung bawah + ujung atas) 30

UKURAN PEMUSATAN 31

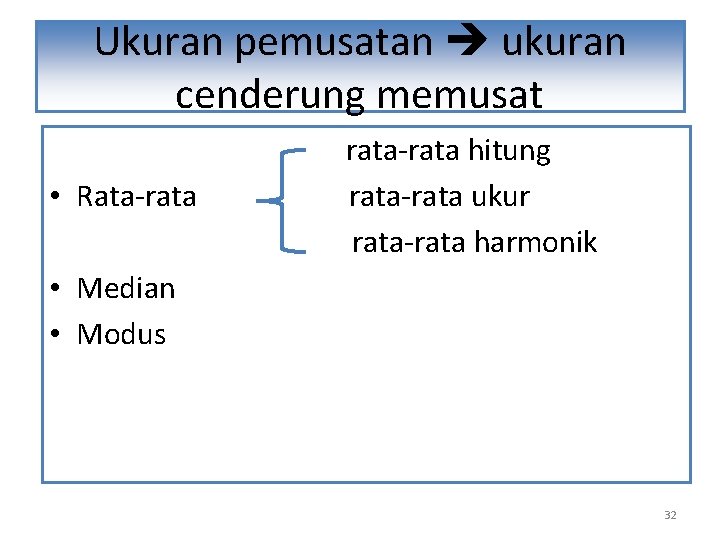
Ukuran pemusatan ukuran cenderung memusat • Rata-rata-rata hitung rata-rata ukur rata-rata harmonik • Median • Modus 32

Rata-rata hitung data tersebar • Data tersebar (tdk berkelompok) 33

Contoh menghitung rata-rata Dari hasil tes 10 siswa kelas XI diperoleh data: 3, 7, 6, 5, 3, 6, 9, 8, 7, dan 6. Tentukan rataan dari data tersebut. Jawab 34

Rata-rata hitung data terkelompok xi : titik tengah kelas interval ke-i fi : frekuensi kelas interval ke-i n : banyaknya data 35

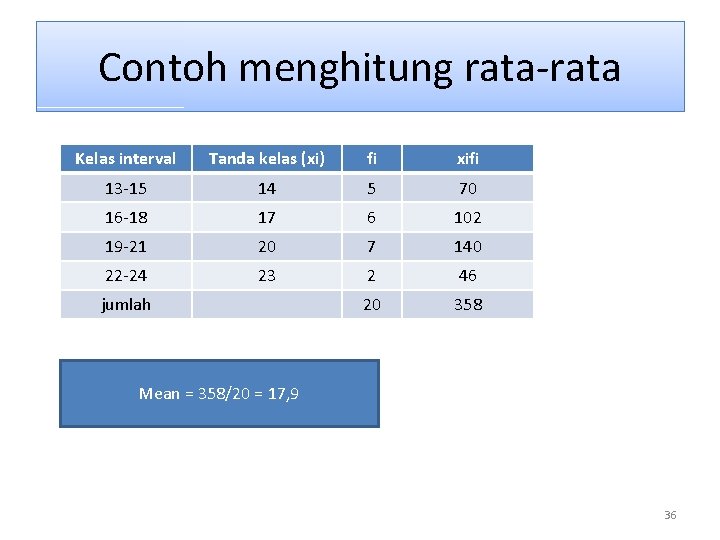
Contoh menghitung rata-rata Kelas interval Tanda kelas (xi) fi xifi 13 -15 14 5 70 16 -18 17 6 102 19 -21 20 7 140 22 -24 23 2 46 20 358 jumlah Mean = 358/20 = 17, 9 36

Modus • Data kualitatif gejala yang sering terjadi • Data kuantitatif angka yang sering muncul 37

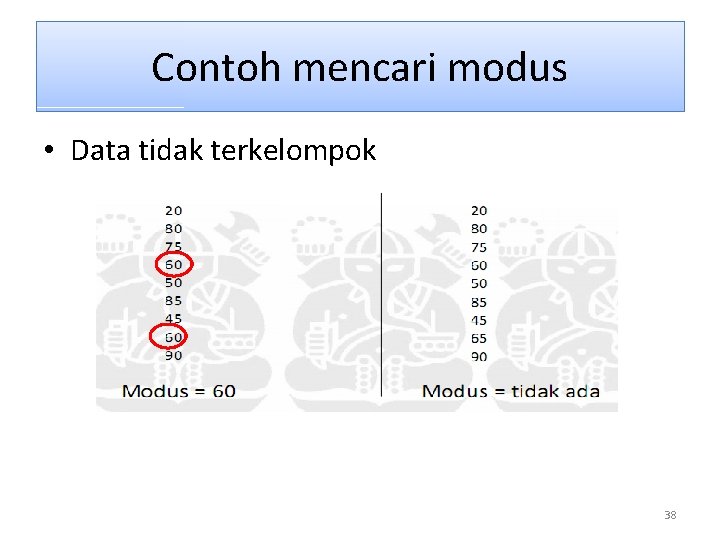
Contoh mencari modus • Data tidak terkelompok 38

Modus pada data terkelompok Mo = Bb + p dengan Bb = batas bawah kelas interval yang mempunyai frekuensi tertinggi b 1 = selisih frekuensi tertinggi dengan frekuensi dari kelas interval yang lebih rendah. b 2 = selisih frekuensi tertinggi dengan frekuensi dari kelas interval yang lebih tinggi. p = panjang kelas. 39

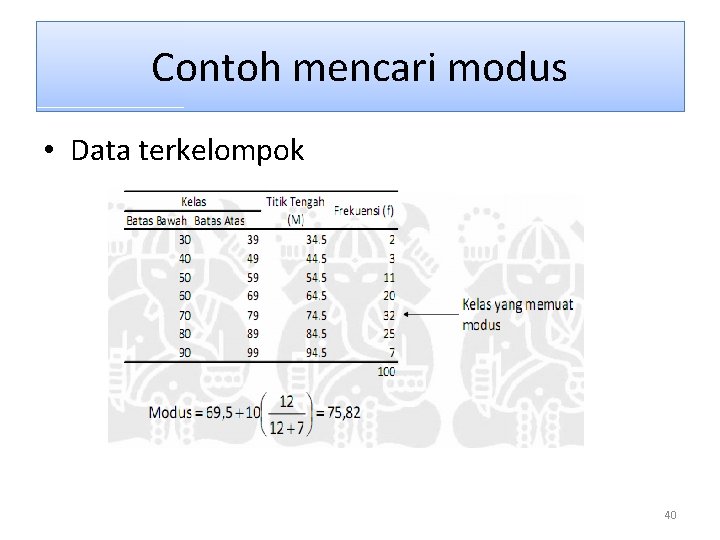
Contoh mencari modus • Data terkelompok 40

Median untuk data tidak terkelompok • Jika banyak data genap Me = • Jika banyak data ganjil Me = Data harus diurutkan dulu dari terkecil ke terbesar 41

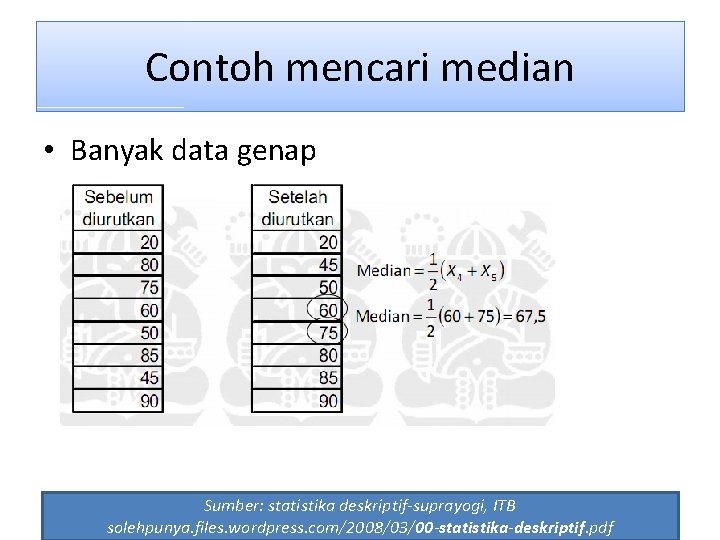
Contoh mencari median • Banyak data genap Sumber: statistika deskriptif-suprayogi, ITB solehpunya. files. wordpress. com/2008/03/00 -statistika-deskriptif. pdf 42

Contoh mencari median • Banyak data ganjil Sumber: statistika deskriptif-suprayogi, ITB solehpunya. files. wordpress. com/2008/03/00 -statistika-deskriptif. pdf 43

Median data terkelompok Me = Bb + p dengan Bb : batas bawah kelas interval yang mengandung Me fm : frekuensi kelas interval yang mengandung Me F : frekuensi kumulatif sebelum kelas interval yang mengandung Me p : panjang kelas interval Letak Me harus paling sedikit mencapai frekuensi setengah dari jumlah data seluruhnya 44

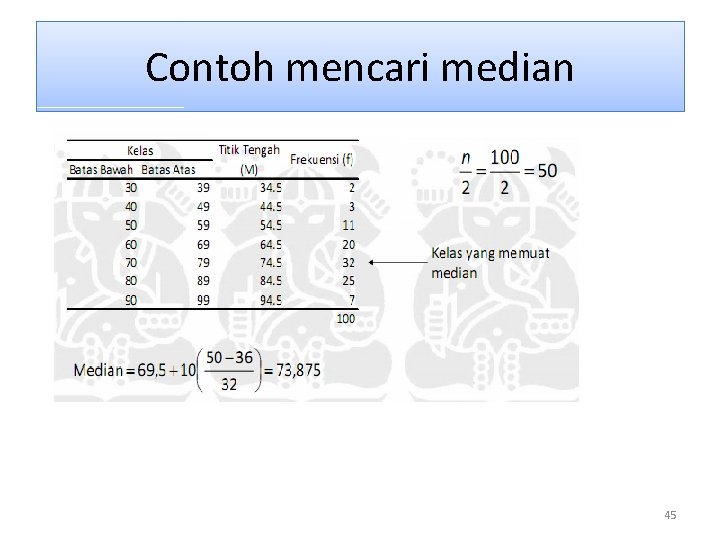
Contoh mencari median 45

Hubungan Mean, Modus dan Median Hubungan empiris antara ketiganya: Mo +2 M = 3 Me 46