Penser la musique dans la logique fonctorielle des











- Slides: 27

Penser la musique dans la logique fonctorielle des topoi Guerino Mazzola U & ETH Zürich Internet Institute for Music Science guerino@mazzola. ch www. encyclospace. org

programme • Topographie musicale • Stratification sémiotique • Models mathématiques • Espaces de concepts • Fiction et facticité • Vérité et beauté

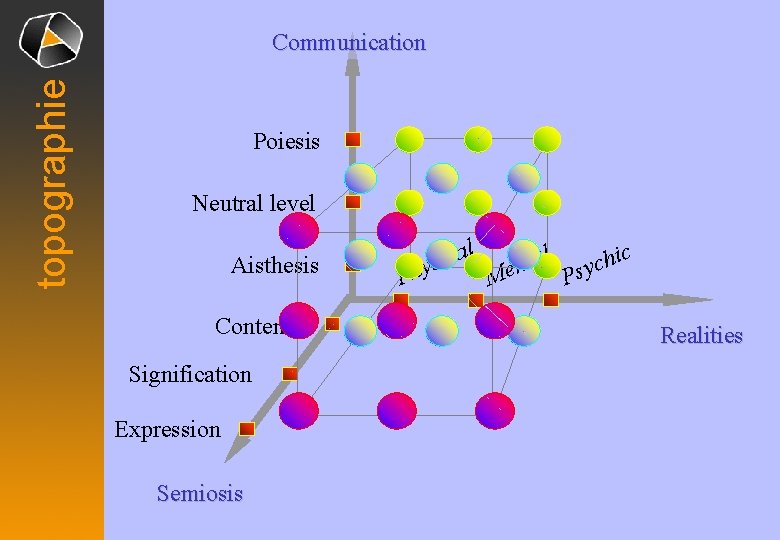
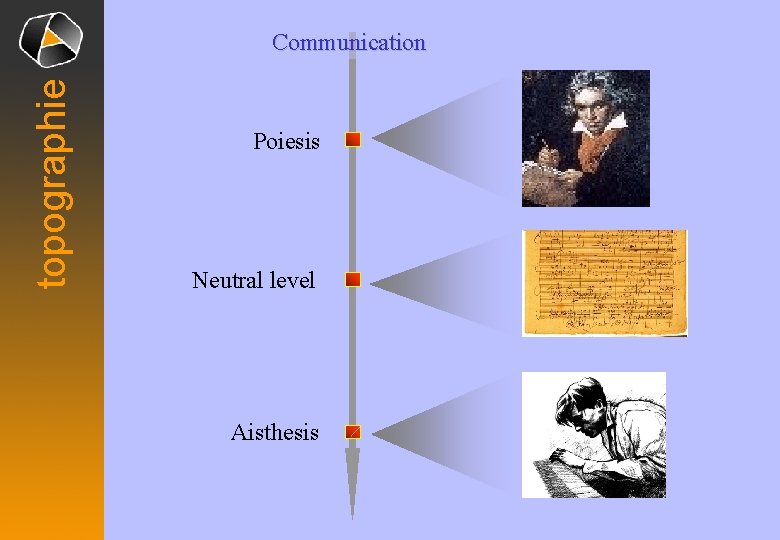
topographie Communication Poiesis Neutral level Aisthesis Content Signification Expression Semiosis l P ica s y h l a t n Me ic h c sy P Realities

topographie Communication Poiesis Neutral level Aisthesis

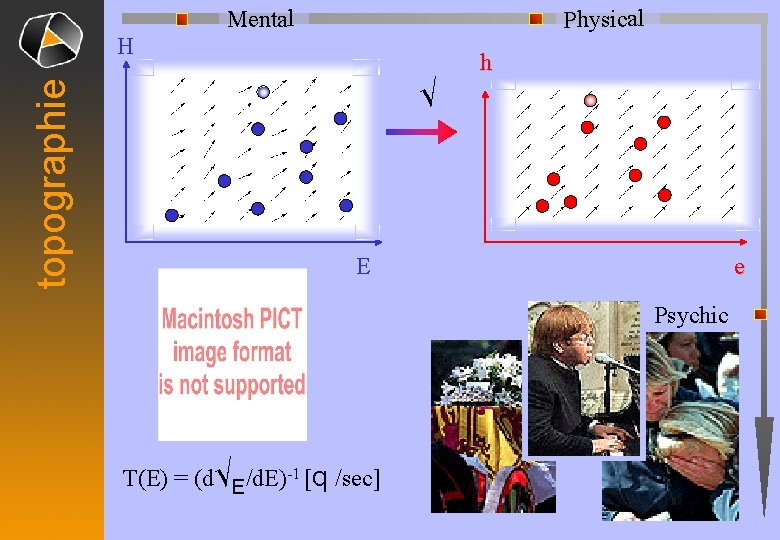
topographie H Physical Mental h √ e E Psychic T(E) = (d√E/d. E)-1 [q /sec]

topographie Expression Score „surface“ Signification Harmonic analysis Content Semiosis Tonal modulation G major ® E b major

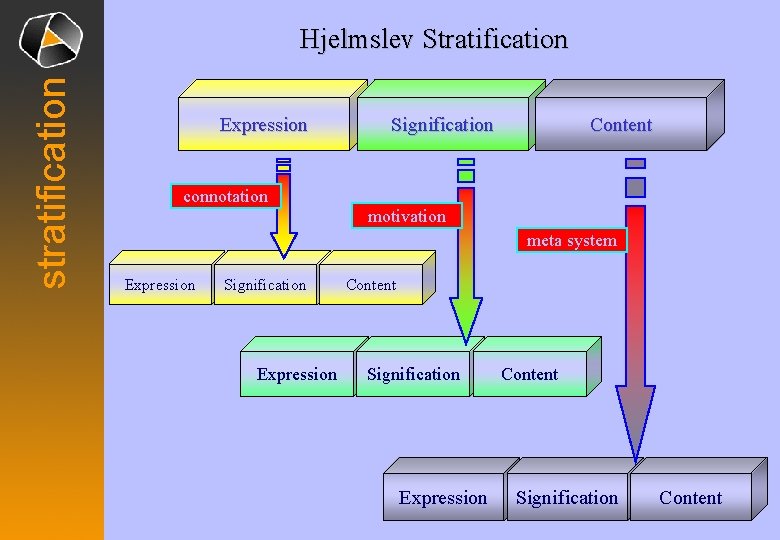
stratification Hjelmslev Stratification Expression Signification Content connotation motivation meta system Expression Signification Expression Content Signification Content

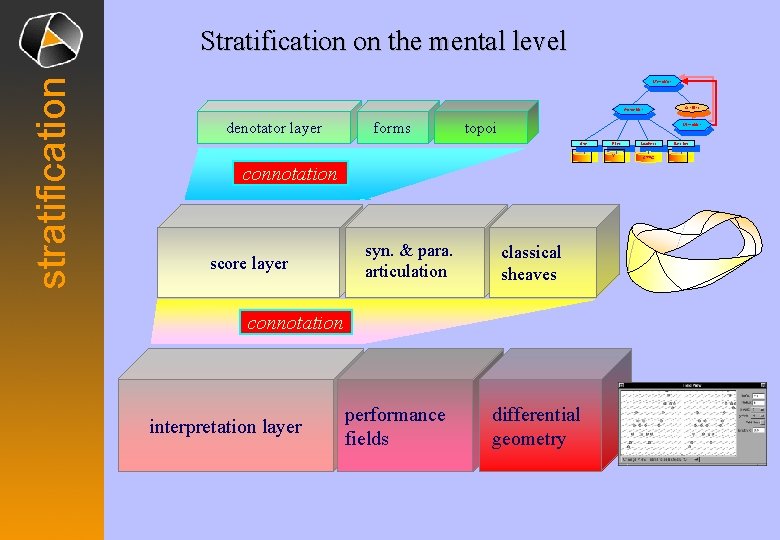
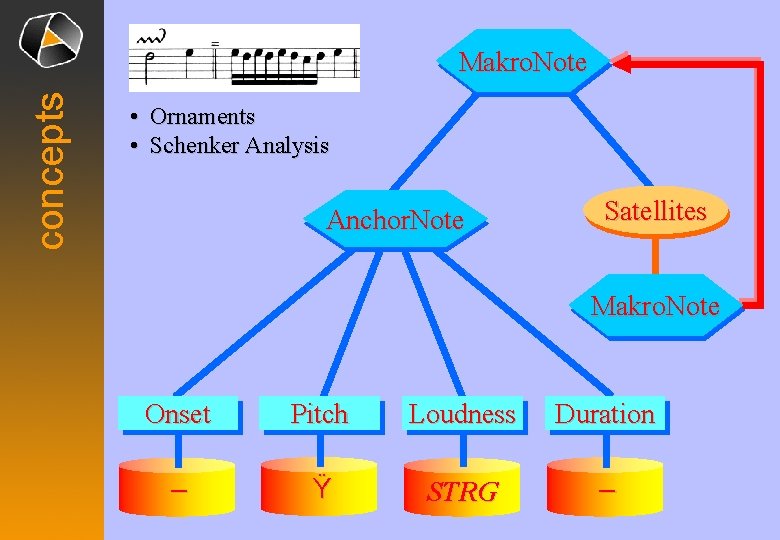
stratification Stratification on the mental level Makro. Note Satellites Anchor. Note denotator layer forms topoi Makro. Note Onset Pitch – Ÿ connotation score layer syn. & para. articulation classical sheaves connotation interpretation layer performance fields differential geometry Loudness STRG Duration –

models What is a mathematical model of a musical phenomenon? Music Mathematics Field of Concepts Precise Concept Framework Material Selection Instance specification Process Type Formal process restatement Grown rules for process • construction and • analysis Proof of structure theorems Deduction of rules from structure theorems Why this material, these rules, relations? Anthropic Principle! Generalization!

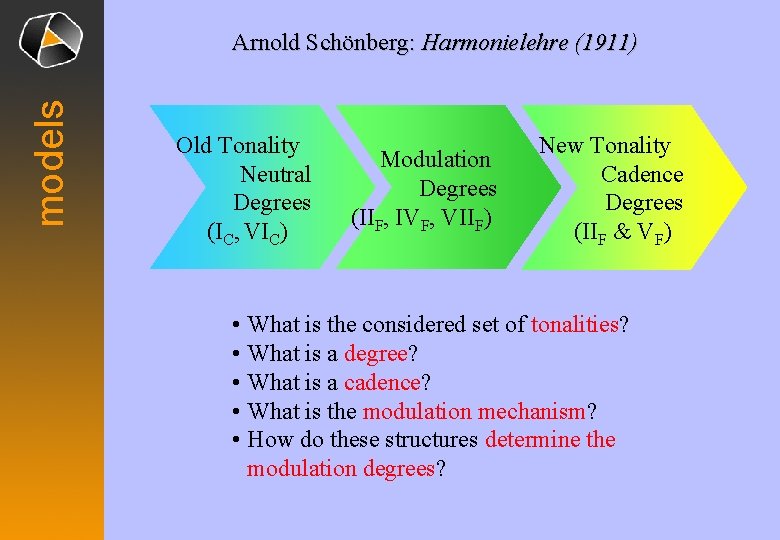
models Arnold Schönberg: Harmonielehre (1911) Old Tonality Neutral Degrees (IC, VIC) Modulation Degrees (IIF, IVF, VIIF) New Tonality Cadence Degrees (IIF & VF) • What is the considered set of tonalities? • What is a degree? • What is a cadence? • What is the modulation mechanism? • How do these structures determine the modulation degrees?

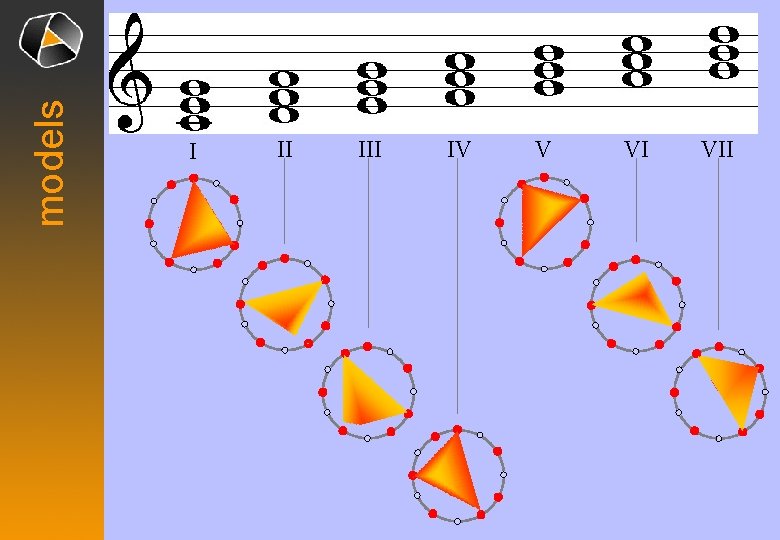
models I II IV V VI VII

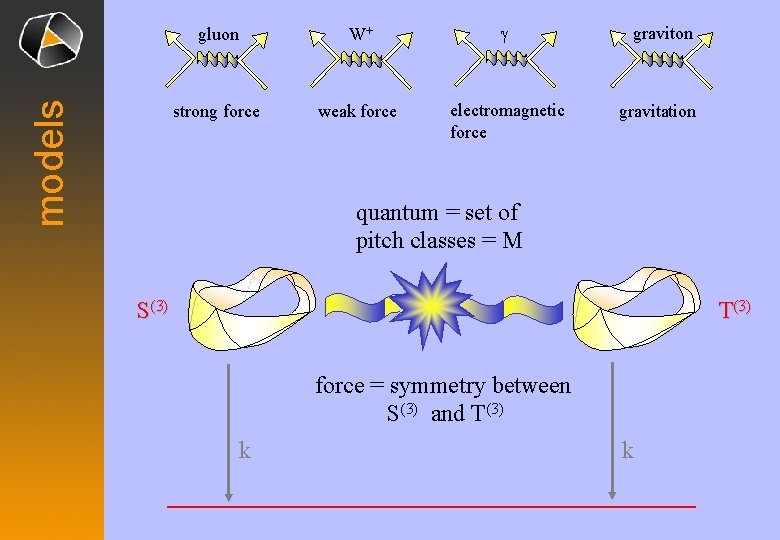
models gluon W+ g strong force weak force electromagnetic force graviton gravitation quantum = set of pitch classes = M S(3) T(3) force = symmetry between S(3) and T(3) k k

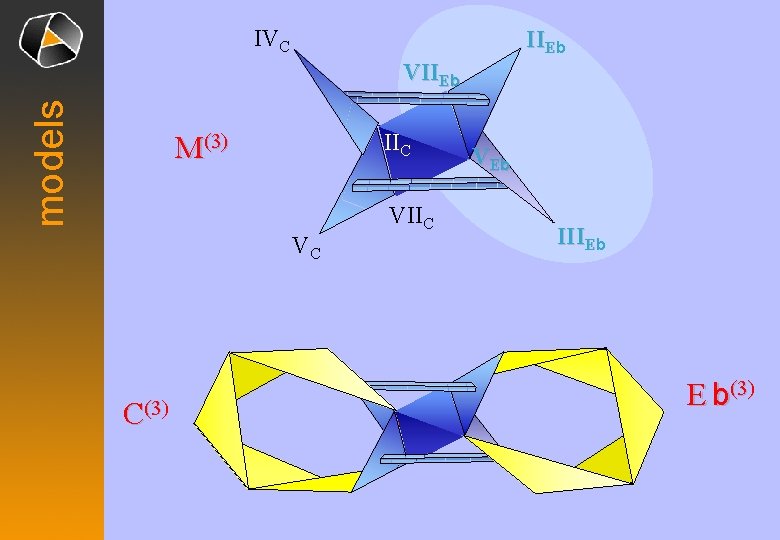
IVC IIEb models VIIEb IIC M(3) VC C(3) VIIC VE b IIIEb E b(3)

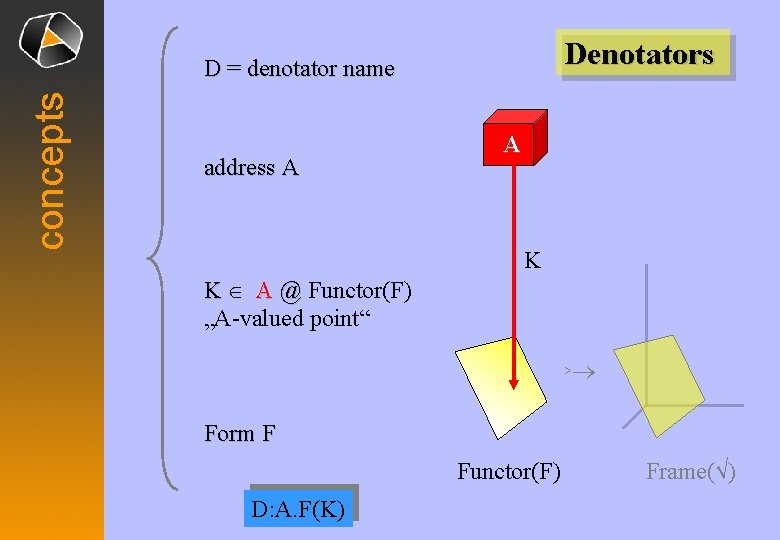
Denotators concepts D = denotator name address A A K K Î A @ Functor(F) „A-valued point“ ® > Form F Functor(F) D: A. F(K) Frame(√)

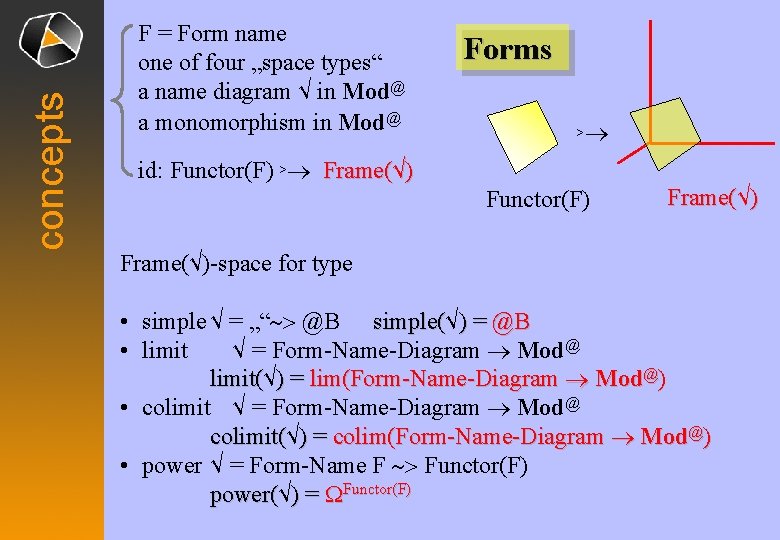
concepts F = Form name one of four „space types“ a name diagram √ in Mod@ a monomorphism in Mod@ Forms ® > id: Functor(F) >® Frame(√) Functor(F) Frame(√)-space for type • simple √ = „“~> @B simple(√ simple( ) = @B • limit √ = Form-Name-Diagram ® Mod@ limit(√ limit( ) = lim(Form-Name-Diagram ® Mod@) • colimit √ = Form-Name-Diagram ® Mod@ colimit(√ colimit( ) = colim(Form-Name-Diagram ® Mod@) • power √ = Form-Name F ~> Functor(F) power(√ power( ) = WFunctor(F)

concepts Makro. Note • Ornaments • Schenker Analysis Anchor. Note Satellites Makro. Note Onset Pitch Loudness Duration – Ÿ STRG –

concepts Galois Theory Form Theory Defining equation Defining diagram f. S(X) = 0 x 1 x 2 x 3 Field S xn id √(F) F 2 F 1 Fr Form System

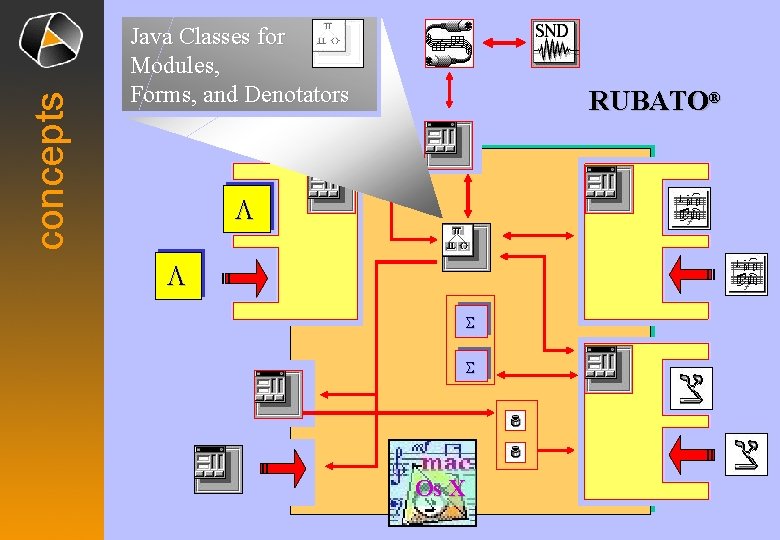
concepts Java Classes for Modules, Forms, and Denotators RUBATO® L L S S Os X

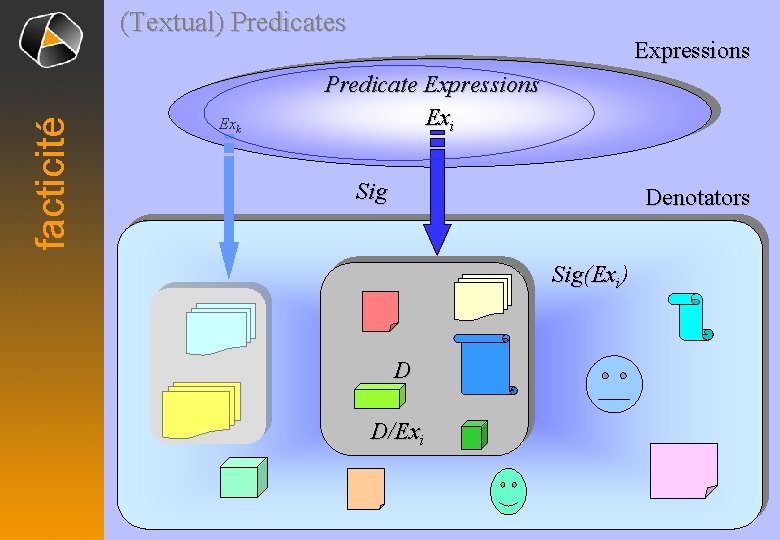
facticité (Textual) Predicates Exk Expressions Predicate Expressions Exi Sig Denotators Sig(Exi) D D/Exi

What is facticity of predicate Ex at denotator D? facticité D/Ex : A. TRUTH(F)(d) TRUTH(F) = space of “subsets” of space F of ‘truth values’ d Î W F(A) d Í @A x F A d F The coordinate d of a truth denotator D/Ex is a ‚sieve‘ in A x F.

facticité Special case 1: I = 0 -module Then F = @0 = final object = 1 in Mod@ d Î W 1(A) = W (A) A = 0: W (0) = Hom(1, W) = set of topos-theoretic truth values = Sub(@0) Special values: d = ˆ = F = ˘ T, d = @0 = T

facticité Special case 2: I = —/Ÿ = S = circle group, F = @S. d Î W F(A) means this: Take again special address A = 0, i. e. , d Í @S e S In particular, if d = d@, d = [0, e[ Í S an interval, we have fuzzy logic defined by the truth quantity e in the closed unit interval.

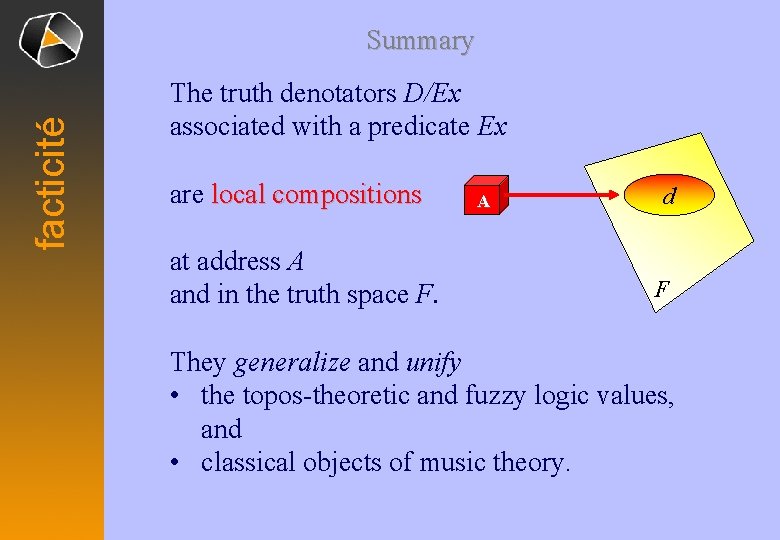
facticité Summary The truth denotators D/Ex associated with a predicate Ex are local compositions at address A and in the truth space F. A d F They generalize and unify • the topos-theoretic and fuzzy logic values, and • classical objects of music theory.

facticité Classification of Predicate Constructions 1. Arbitrary/Atomic Predicates: • Mathematical • Musical (Primavista) • Deictic (Shifters) 2. Motivated/Compound Predicates: • Logical • Geometric D/Ex

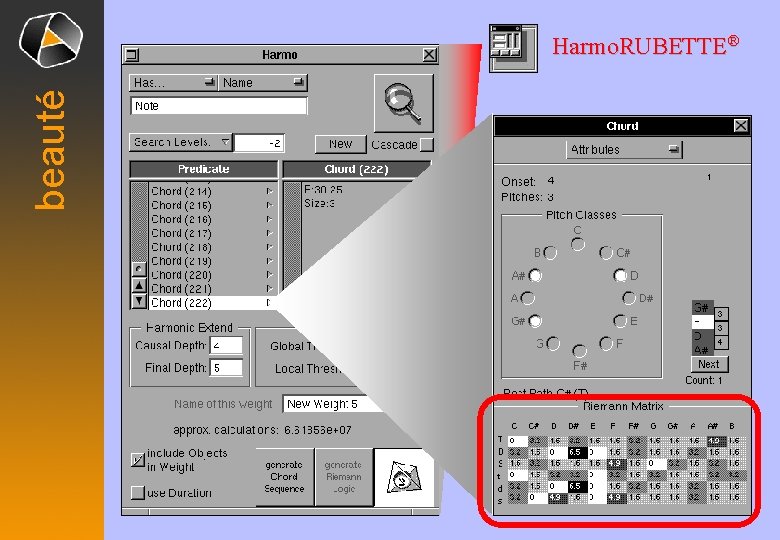
beauté Harmo. RUBETTE®

beauté TON = {C, F, A# , D# , G# , C# , F#, B, E, A, D, G} val= {T, S, D, t, s, d} S = —/Ÿ F= @S, A = 0 T, v = D# , d Rie. MD#, d(Chord(222)) = d@, d = [0, e[ Í S

beauté TON = {C, F, A# , D# , G# , C# , F#, B, E, A, D, G} Val= {T, S, D, t, s, d, T*, S*, D*, t*, s*, d*} F = Chords(Ÿ 12) TRUTH(F) = sets of chords in F Rie. NT, v(Chord) = d. Chord. Ext 0(MT, v) MT, v = monoid of all endomorphisms of prototypical triadic chords Ext 0(MT, v) = {chords invariant under MT, v} = basic open set in the extension topology
 6 chapeaux pour penser
6 chapeaux pour penser Couché avec mes soeurs j'ai la tete rouge
Couché avec mes soeurs j'ai la tete rouge Des des des
Des des des La musique est la langue des émotions
La musique est la langue des émotions Qui veut gagner des millions 50/50
Qui veut gagner des millions 50/50 Il y a des moments dans la vie
Il y a des moments dans la vie Remerciements de rapport de stage
Remerciements de rapport de stage La famille des cochons ramenée dans l'étable analyse
La famille des cochons ramenée dans l'étable analyse Il est des moments dans la vie
Il est des moments dans la vie Schéma du passage des nutriments dans le sang
Schéma du passage des nutriments dans le sang Il est des moments dans la vie
Il est des moments dans la vie Il y a des moments dans la vie
Il y a des moments dans la vie Nous sommes les étoiles dans le ciel d'abraham
Nous sommes les étoiles dans le ciel d'abraham La situation initiale d'un conte
La situation initiale d'un conte Trajet des aliments dans le corps
Trajet des aliments dans le corps Logique floue
Logique floue Exemple de cadre logique d'un projet agricole
Exemple de cadre logique d'un projet agricole Fonction logique
Fonction logique Logique booléenne
Logique booléenne Fonction oui
Fonction oui Logique de hoare
Logique de hoare Logique interne tennis de table
Logique interne tennis de table Subordonnant exemple
Subordonnant exemple Devinette logique
Devinette logique Adverbes de relation logique
Adverbes de relation logique Logique interne danse
Logique interne danse Excel test logique
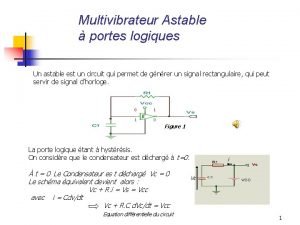
Excel test logique Astable à porte logique
Astable à porte logique