PENGUKURAN RISIKO TEORI PROBABILITAS DERAJAT RISIKO VALUE AT

PENGUKURAN RISIKO TEORI PROBABILITAS DERAJAT RISIKO VALUE AT RISK Resista Vikaliana 4/12/2013 1

TEORI PROBABILITAS Resista Vikaliana 4/12/2013 2

Pengukuran Risiko � Tujuan pengukuran risiko: � Nilai rata-rata dari kerugian selama suatu periode anggaran � Variasi nilai kerugian dari satu periode anggaran ke periode anggaran yang lain � Dampak keseluruhan dari kerugian-kerugian tersebut, terutama kerugian yang ditanggung sendiri Resista Vikaliana 4/12/2013 3

� Dimensi yang diukur: � Besarnya kemungkinan kejadian � Besarnya kerugian bila suatu risiko terjadi Resista Vikaliana 4/12/2013 4

Konsep Probabilitas dalam Pengukuran Kerugian Potensial � Sample Space dan Event � Sample Space (Set S): � Suatu rangkaian dari kejadian tertentu yang diamati, misalnya jumlah kecelakaan mobil di wilayah tertentu selama periode tertentu. � Bisa terdiri dari beberapa segmen (sub-set) atau event (Set E) � Setiap Set E diberi bobot. Bobot berdasarkan bukti empiris masa lalu. Resista Vikaliana 4/12/2013 5

� Misal pada kecelakaan mobil, mobil pribadi diberi bobot 2, sedangkan mobil penumpang umum diberi bobot 1, sehingga bobotnya � Bila tanpa bobot P (E) = E/S � Bila dengan bobot P (E) = W (E)/W (S) � P(E) �E �S �W : : probabilitas terjadinya event sub set atau event sample space atau set bobot dari masing-masing event Resista Vikaliana 4/12/2013 6

� Contoh : � Seorang kontraktor diminta untuk membangun sebuah gedung. Apabila segala sesuatu berjalan dengan baik, maka ia akan mendapatkan keuntungan sebesar Rp 10. 000. � Karena menyadari selalu adanya hal-hal yang tidak terduga, maka probabilitas untuk mendapatkan keuntungan tersebut diperkirakan hanya 80%, dimana yang 20% adalah pengeluaran tak terduga. Resista Vikaliana 4/12/2013 7

� Dari data itu, pihak kontraktor dapat mempertimbangkan kesempatan-kesempatan atau kemungkinan-kemungkinan lain sehubungan dengan perputaran, misalnya. � Bisa juga dengan mengalihkan ke pihak lain, misal perusahaan asuransi Resista Vikaliana 4/12/2013 8

� COMPOUND EVENTS � Terjadinya dua atau lebih peristiwa terpisah dalam jangka waktu yang sama � Compound Event yang Bebas � Jika terjadinya satu peristiwa tidak ada hubungannya dengan peristiwa lain � Compound Event Bersyarat � Jika terjadinya peristiwa yang satu mempengaruhi terjadinya peristiwa yang lain Resista Vikaliana 4/12/2013 9

� CONTOH Compound Event yang Bebas � Probabilitas terbakarnya gudang A tidak dipengaruhi oleh terbakarnya gedung B. Bila probabilitas terbakarnya gudang A adalah 1/10 dan gudang B adalah 1/30, maka probabilitas terbakarnya gudang A dan gudang B adalah � 1/10 x 1/30 = 1/300 � Jadi, P (A dan B) = P (A) x P (B) Resista Vikaliana 4/12/2013 10

Probabilitas dari semua kemungkinan kejadian adalah � Kemungkinan I: � Gudang A terbakar dan gudang B tidak terbakar adalah (1/10) x(1 -1/30) = 29/300 � Kemungkinan II: � Gudang A tidak terbakar, tetapi gudang B terbakar adalah (1 -1/10) x (1/30) = 9/300 � Kemungkinan III: � Gudang A dan gudang B tidak terbakar adalah � (1 -1/10) x (1 -1/30) = 261/300 � Kemungkinan IV: � Gudang A dan gudang B terbakar adalah (1/10) x (1/30) =1/300 � � Jumlah probabilitas keempat kemungkinan kejadian tersebut adalah 300/300 = 1 Resista Vikaliana 4/12/2013 11

� CONTOH compound event bersyarat � Perusahaan Y mempunyai dua gudang yang berdekatan, yaitu A dan B. Kebakaran pada gudang A akan mempengaruhi gudang B. � Bila probabilitas terbakarnya gudang A adalah 1/40 dan probabilitas terbakarnya gudang B juga 1/40, serta probabilitas terbakarnya gudang B setelah gudang A terbakar atau P(B/A) adalah 1/3, maka probabilitasnya Resista Vikaliana 4/12/2013 12

Latihan (1) � Bila probabilitas terbakarnya gudang A adalah 1/35 dan probabilitas terbakarnya gudang B juga 1/55, serta probabilitas terbakarnya gudang B setelah gudang A terbakar atau P(B/A) adalah 1/4, maka probabilitasnya Resista Vikaliana 4/12/2013 13

Probabilitas � Kemungkinan I: � Gudang A terbakar dan gudang B terbakar adalah (1/40) x(1/3) = 1/120 � Kemungkinan II: � Gudang A terbakar, tetapi gudang B tidak terbakar adalah 1/40 x (1 -1/3) = 2/120 � Kemungkinan III: � Gudang A tidak terbakar dan gudang B terbakar adalah � (1 -1/40) x 1/3 = 39/120 � Kemungkinan IV: � Gudang A tidak terbakar dan gudang B tidak terbakar adalah (1 -1/40) x (1 -1/3) = 78/120 � � Jumlah probabilitas keempat kemungkinan kejadian tersebut adalah 120/120=1 Resista Vikaliana 4/12/2013 14

� Event yang independen dan acak � Prinsip keacakan (setiap event mempunyai kesempatan dan probabilitas yang sama) dan independensi/ berdiri sendiri mempunyai peran yang penting, khususnya pada bidang asuransi, karena: � Underwriter/ perusahaan asuransi akan berusaha untuk mengklasifikasikan unit-unit esposures ke dalam kelompok-kelompok, di mana kejadian atau kerugian dapat dianggap sebagai event yang independen. Resista Vikaliana 4/12/2013 15

� PENGUKURAN BESARNYA KERUGIAN � pengukuran sebaiknya dilakukan dengan menggunakan satuan uang � Dalam hal tertentu kadang-kadang juga digunakan skala, misal skala 1 -5 � 1 : kerugian yang sangat kecil � 2 : kerugian yang kecil � 3 : kerugian menengah � 4 : kerugian besar � 5 : kerugian sangat besar Resista Vikaliana 4/12/2013 16

� KEMUNGKINAN (LIKELIHOOD) TERJADI KECELAKAAN ◦ Likelihood: Kesempatan akan terjadinya sesuatu benar-benar terjadi � Kategori ◦ ◦ likelihood: Very likely : mungkin terjadi berkali-kali Likely : mungkin terjadi kadang-kadang Unlikely : mungkin terjadi, tetapi jarang Highly unlikely: mungkin terjadi tetapi sangat tidak mungkin pernah terjadi Resista Vikaliana 4/12/2013 17

� Untuk mengevaluasi likelihood kecelakaan, faktor yang memodifikasi kategori tersebut adalah ancaman: ◦ ◦ ◦ Very rare: sekali dalam setahun atau kurang Rare : beberapa kali dalam setahun Unusual : sekali dalam setahun Occasional : sekali seminggu Frequent : setiap hari Continuous: terus menerus Resista Vikaliana 4/12/2013 18

� Contoh : mesin pencetak lubang besi � Operatornya menghadapi risiko cedera/ kecelakaan satu kali dalam 34, 75 minggu. Ancaman risikonya “very rare” tetapi “likely” terjadi kecelakaan (cedera) hampir pasti terjadi kesalahan pengendalian Resista Vikaliana 4/12/2013 19

� Konsekuensi/ Akibat kejadian: � Fatal : kematian � Major injuries : kerugian luka-luka yang tidak dapat diubah atau gangguan kesehatan yang membutuhkan waktu lama dalam perbaikan � Minor injuries : luka-luka bisa diubah, atau gangguan kesehatan hanya dalam hitungan hari � Negligible injuries : cukup dengan pertolongan pertama dapat kembali berfungsi seperti biasa Resista Vikaliana 4/12/2013 20

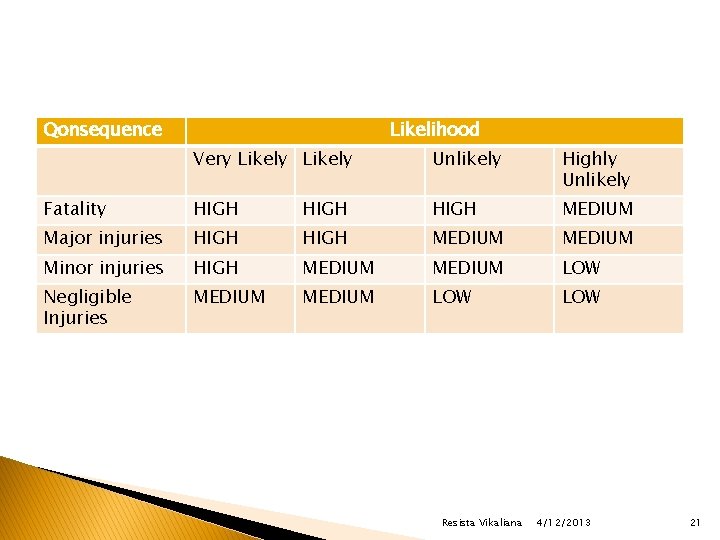
Qonsequence Likelihood Very Likely Unlikely Highly Unlikely Fatality HIGH MEDIUM Major injuries HIGH MEDIUM Minor injuries HIGH MEDIUM LOW Negligible Injuries MEDIUM LOW Resista Vikaliana 4/12/2013 21

� Setiap kejadian merugikan, terdapat dampak langsung dan tidak langsung � Untuk kerugian langsung, terdapat beberapa konsep yang dapat digunakan: nilai perolehan, nilai buku, nilai pasar dan nilai ganti � Untuk kerugian tidak lansung, antara lain berupa biaya sewa dan berkurangnya pendapatan (sebagian kerugian langsung sangat sulit ditentukan) Resista Vikaliana 4/12/2013 22

Derajat Risiko Resista Vikaliana 4/12/2013 23

� Besarnya risiko objektif yang timbul dalam satu situasi � Objective � Probable variation of actual from expected losses � Expected losses � � Simpangan kemungkinan kerugian aktual dengan kerugian yang diharapkan Risk= ------------� Kerugian yang diharapkan Resista Vikaliana 4/12/2013 24

� � � Misal : Kemungkinan kerugian karena kebakaran bangunan di Kota ABC dan XYZ dengan jumlah bangunan setiap kota 100. 000. Rata-rata bangunan terbakar setiap tahun pada tiap kota adalah 100 bangunan. Ahli statistik mengestimasi jumlah kebakaran pada Kota ABC tahun depan adalah 95105 bangunan. Kisaran pada Kota XYZ 80 -120 Maka, derajat bangunan terbakar pada masing –masing kota adalah Risiko ABC (105 -95)/100 = 10 % Risiko XYZ (120 -80)/100 = 40 % Resista Vikaliana 4/12/2013 25

� JIKA PROBABILITAS TIDAK DAPAT DIPERKIRAKAN � Meminimumkan kerugian potensial yang maksimum selama periode yang bersangkutan (minimax) ◦ Memilih keputusan yang memberi kerugian paling kecil � Meminimumkan kerugian potensial yang minimum dalam periode yang bersangkutan (minimin) ◦ Memilih kerugian yang paling kecil (tidak melihat outcome) Resista Vikaliana 4/12/2013 26

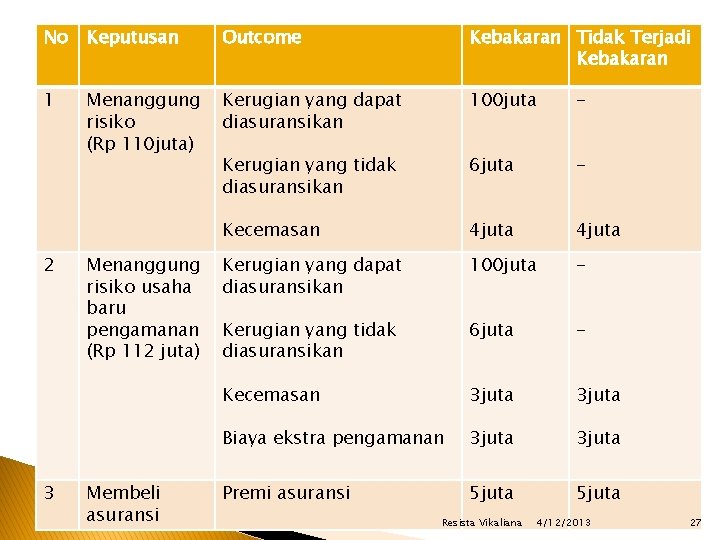
No Keputusan Outcome Kebakaran Tidak Terjadi Kebakaran 1 Menanggung risiko (Rp 110 juta) Kerugian yang dapat diasuransikan 100 juta - Kerugian yang tidak diasuransikan 6 juta - Kecemasan 4 juta Kerugian yang dapat diasuransikan 100 juta - Kerugian yang tidak diasuransikan 6 juta - Kecemasan 3 juta Biaya ekstra pengamanan 3 juta Premi asuransi 5 juta 2 3 Menanggung risiko usaha baru pengamanan (Rp 112 juta) Membeli asuransi Resista Vikaliana 4/12/2013 27

VALUE AT RISK Resista Vikaliana 4/12/2013 28

VALUE AT RISK � Ada tiga metode perhitungan Value at Risk yaitu: � Metode historis � Metode variance-covariance � Metode dengan simulasi Monte Carlo. Resista Vikaliana 4/12/2013 29

� Sekarang istilah statistik kita nyatakan dalam persentase dan rupiah : � Dengan tingkat kepercayaan 95%, kita berharap kerugian harian terburuk tidak akan melebihi 4%. � Jika kita investasi sebesar Rp. 100 juta, kita percaya 95% bahwa kerugian harian terburuk tidak akan melebihi Rp. 4 juta (Rp. 100 juta x -4%). Jika kita ingin menaikkan tingkat kepercayaan, kita perlu memindahkan ke kiri pada grafik histogram yang sama. Pada return -8% dan -7% merupakan 1% return terburuk harian atau dinyatakan dalam kalimat : Dengan tingkat kepercayaan 99%, kita berharap bahwa kerugian ahrian terburuk tidak akan melebihi 7%. Atau jika kita investasi Rp. 100 juta, kita percaya 99% bahwa kerugian harian terburuk tidak akan melebihi Rp. 7 Resista juta. Vikaliana 4/12/2013 30

Metode Variance – Covariance � Metode ini mengansumsikan bahwa return saham QQQ memiliki distribusi normal dengan demikian kita hanya memerlukan estimasi dua faktor yaitu expected return (rata-rata return) dan standar deviasi return. � Ide dibalik variance – covariance adalah sama dengan metode historis, kecuali kita menggunakan kurva normal bukan data actual. � Keunggulan kurva normal, kita secara otomatis mengetahui di mana letak 5% atau 1% return terburuk dalam kurva. Berikut ini hasil distribusi return harian saham QQQ Resista Vikaliana 4/12/2013 31

� 5% dan 1% return terburuk merupakan fungsi dari tingkat kepercayaan dan standar deviasi (σ) � Nilai kepercayaan 95% memberikan nilai faktor (confidence factor) 1. 65 dengan asumsi distribusi normal, begitu juga tingkat kepercayaan 99% memberikan nilai faktor 2. 33. � Jika diketahui bahwa standar deviasi dari distribusi return harian saham QQQ adalah 2. 645, maka besarnya Value at Risk dapat dihitung seperti tabel di bawah ini: Resista Vikaliana 4/12/2013 32

Confidence #of standard Deviations (σ) 95% (high) -1. 65 x σ 99% (really high) -2. 33 x σ Nilai kepercayaan 95% memberikan nilai faktor (confidence factor) 1. 65 dengan asumsi distribusi normal, begitu juga tingkat kepercayaan 99% memberikan nilai faktor 2. 33. Resista Vikaliana 4/12/2013 33

� Jika diketahui bahwa standar deviasi dari distribusi return harian saham QQQ adalah 2. 645, maka besarnya Value at Risk dapat dihitung seperti tabel dibawah ini: Confidence 95% (high) 99% (really high) # of σ -1. 65 x σ -2. 33 x σ Calculation Equals: -1. 65 x (2. 64%) -4. 36 -2. 33 x (2. 64%) -6. 16 Dengan tingkat kepercayaan 95%, kita berharap bahwa kerugian harian terburuk tidak melebihi 4. 36% � Dengan tingkat kepercayaan 99%, kita berharap bahwa kerugian harian terburuk tidak melebihi 6. 16% � Resista Vikaliana 4/12/2013 34

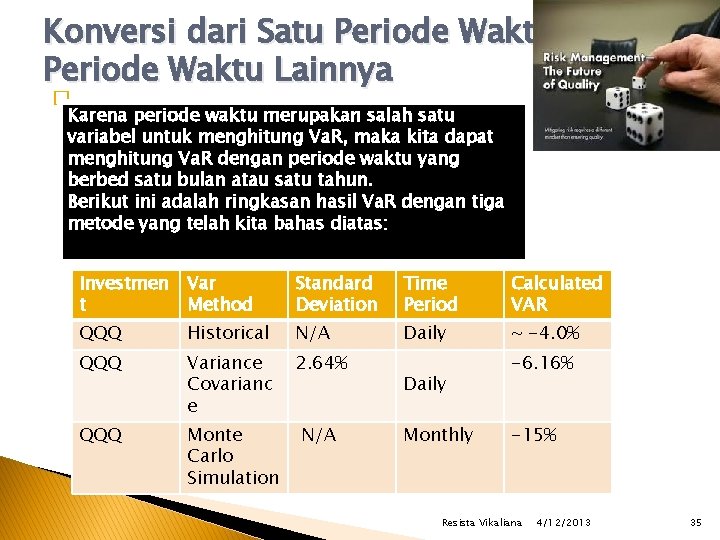
Konversi dari Satu Periode Waktu ke Periode Waktu Lainnya � Karena periode waktu merupakan salah satu variabel untuk menghitung Va. R, maka kita dapat menghitung Va. R dengan periode waktu yang berbed satu bulan atau satu tahun. Berikut ini adalah ringkasan hasil Va. R dengan tiga metode yang telah kita bahas diatas: Investmen t Var Method Standard Deviation Time Period Calculated VAR QQQ Historical N/A Daily ~ -4. 0% QQQ Variance Covarianc e 2. 64% QQQ Monte Carlo Simulation N/A Daily Monthly -6. 16% -15% Resista Vikaliana 4/12/2013 35

Latihan (2) � Jika diketahui bahwa standar deviasi dari distribusi return harian saham YYY adalah 3. 125, hitung Value at Risk (Va. R) saham tersebut pada tingkat kepercayaan 95% dan 99%! � Ubah ke standar deviasi bulanan/ monthly Resista Vikaliana 4/12/2013 36

� Pengguna Va. R dapat mengkonversikan satu periode waktu ke periode waktu lainnya dengan mendasarkan pada ide klasik di ilmu manajemen keuangan yang menyatakan bahwa standar deviasi return suatu saham cenderung meningkat sebesar akar kuadrat dari waktu. Jika standar deviasi return harian adalah 2. 64% dan ada 20 hari perdagangan dalam satu bulan (T = 20), maka standar deviasi bulanan dapat dihitung sebagai berikut: σMonthly = σDaily x T = 2. 64% x 20 Resista Vikaliana 4/12/2013 37

� Untuk mengubah standar deviasi harian menjadi standar deviasi bulanan kita tidak mengalikan dengan angka 20, tetapi dengan akar 20. � Dengan cara yang sama jika kita ingin merubah standar deviasi harian menjadi tahunan (asumsi ada 250 hari perdagangan dalam setahun), maka standar deviasi harian dikalikan dengan akar 250. � Sedangkan merubah standar deviasi bulanan menjadi tahunan dikalikan dengan akar 12. Resista Vikaliana 4/12/2013 38

Referensi Manajemen Risiko pada Perusahaan dan Birokrasi. Hinsa Siahaan. 2009. Elex Media Komputindo, Jakarta. � Manajemen Risiko Bisnis. Tony Pramana. 2011. Sinar Ilmu Publishing, Jakarta � Manajmen Risiko. Herman Darmawi. 2013. Bumi Aksara, Jakarta � Risk management: Pendekatan Kualitatif untuk Bank Komersial. Robert Tampubolon. 2004. Elex Media Komputindo, Jakarta. � Manajemen Risiko(Teori, Kasus dan Solusi). 2011. Alfabeta, Bandung � Manajemen Risiko Perbankan (Bank Jateng). Imam Ghozali (Direktur Program Doktor Ilmu Ekonomi Universitas Diponegoro). 2007. Badan Penerbit Universitas Diponegoro, Semarang. � Manajemen Risiko Finansial. T. Sunaryo. 2007. Penerbit Salemba Empat, Jakarta. � Resista Vikaliana 4/12/2013 39