Pengukuran Poligon KEGUNAAN POLIGON 1 Sebagai kerangka Horizontal

Pengukuran Poligon

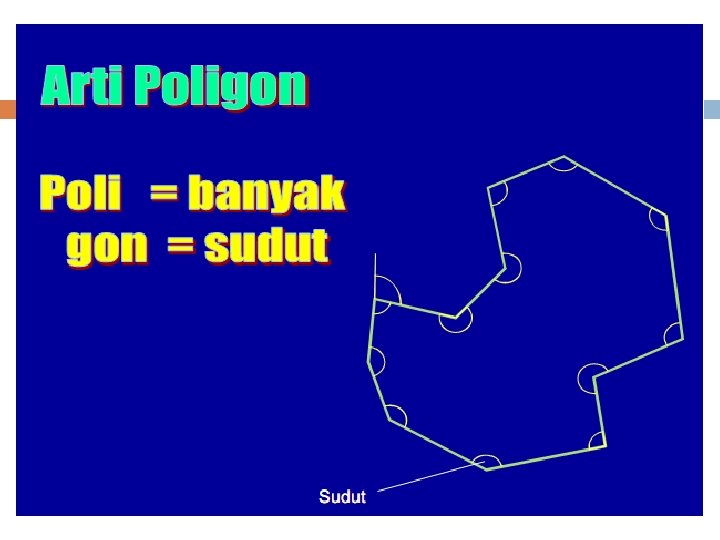
KEGUNAAN POLIGON 1. Sebagai kerangka Horizontal pada daerah pengukuran 2. Kontrol Jarak dan Sudut 3. Basik titik untuk pengukuran selanjutnya 4. Memudahkan dalam perhitungan dan ploting peta SYARAT POLIGON 1. Jurusan Awal 2. Koordinat Awal 3. Semua sudut diukur 4. Semua jarak diukur

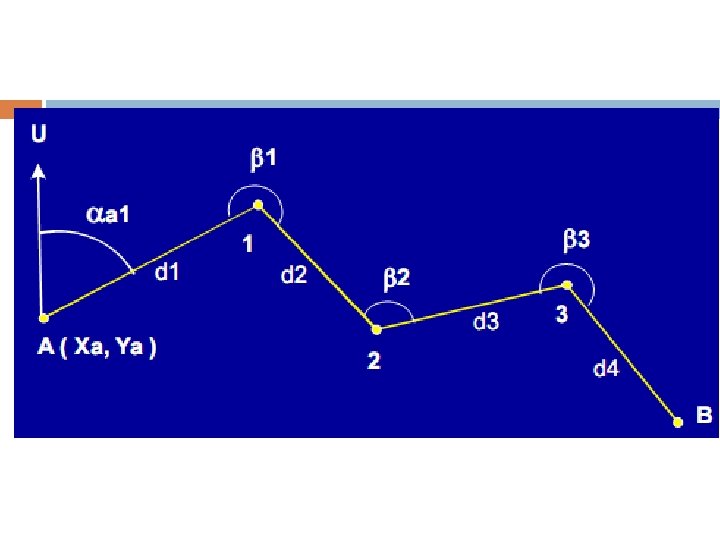
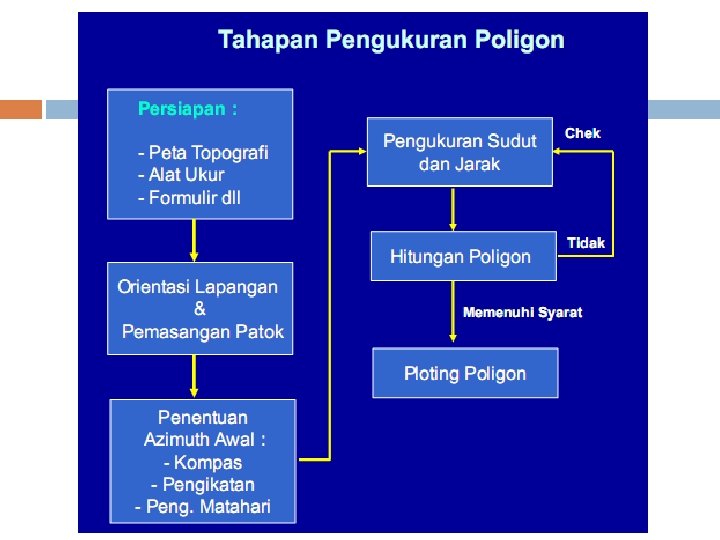
Pada masa kini pengukuran poligon banyak mempergunakan TS ( Total Station ) dimana sudut dan jarak diukur bersamaan kemudian datanya direkam dalam peranti khusus ( disket, Chip ) dan dapat langsung di proses oleh komputer Contoh Alat TS :

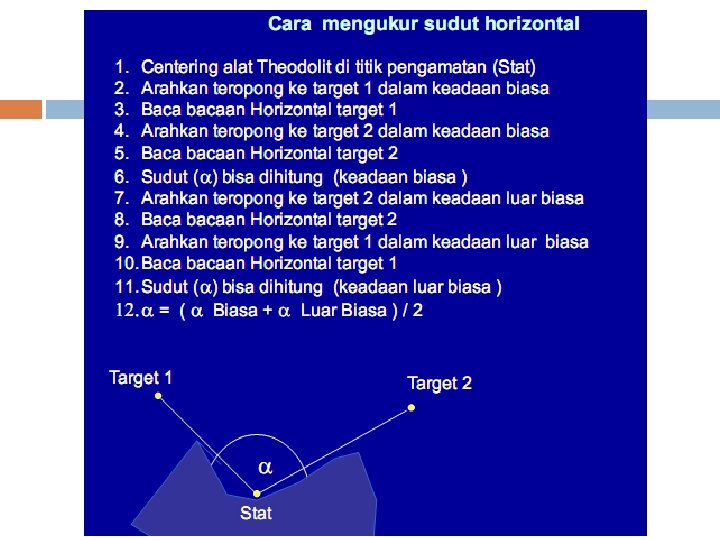
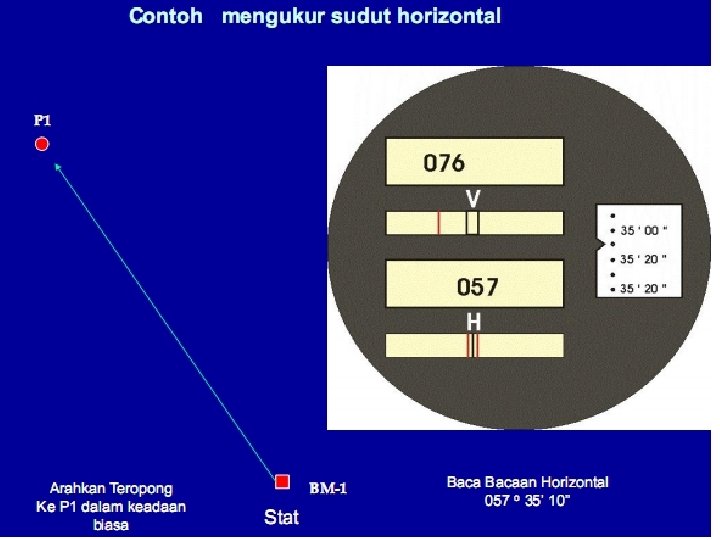
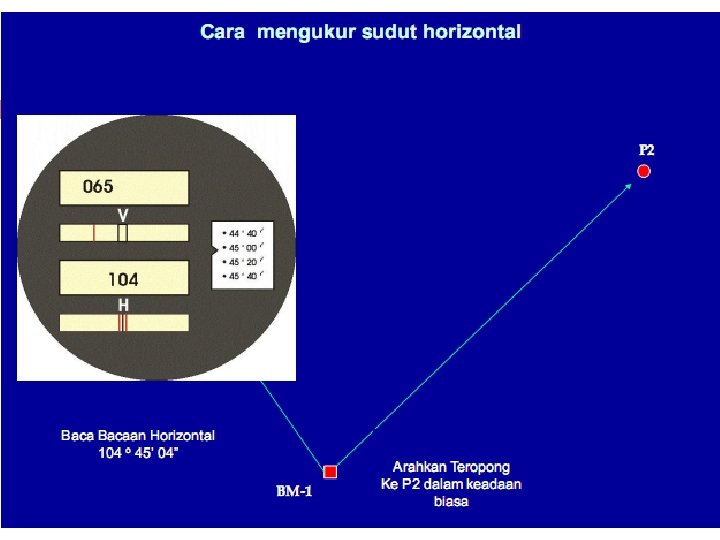
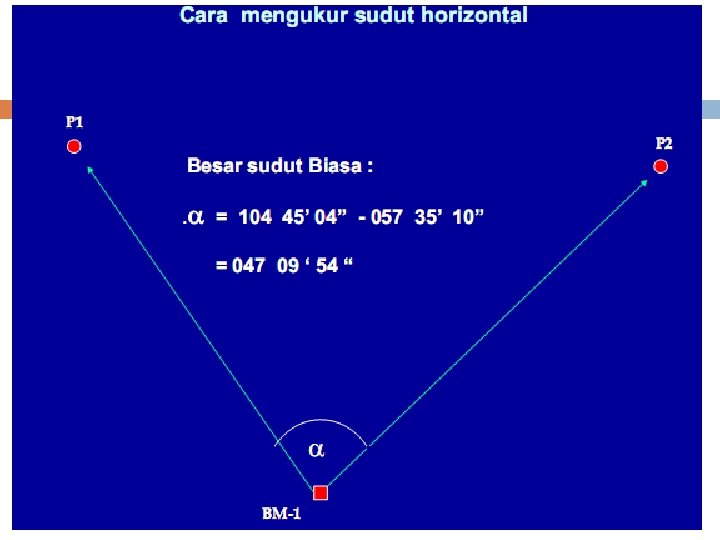
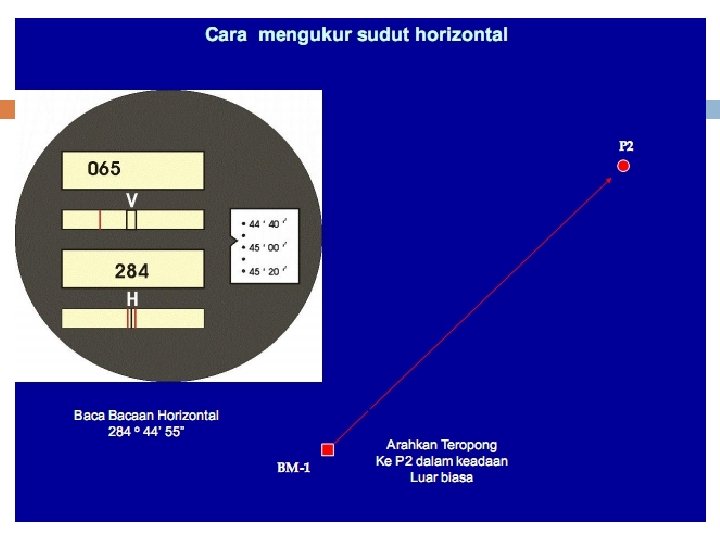
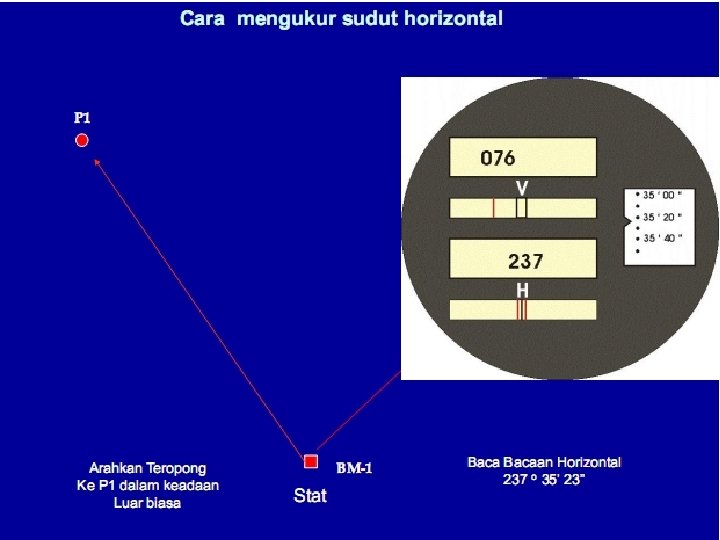
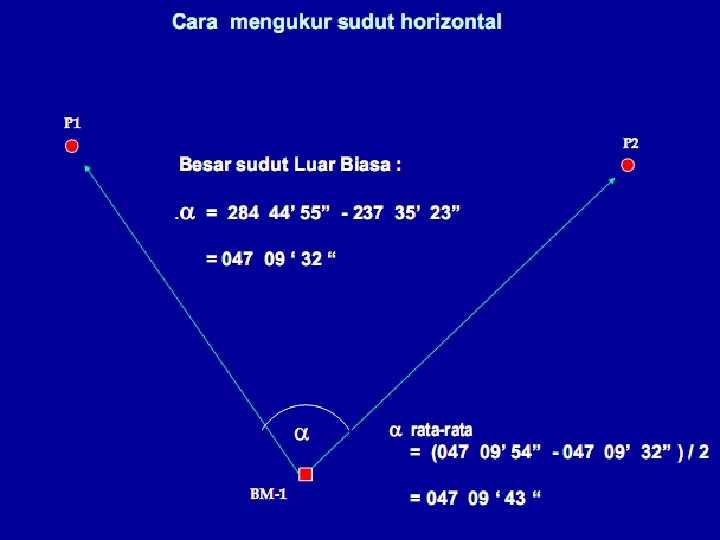
Bentuk Pengukuran Polygon tertutup/keliling Polygon terbuka v Polygon tertutup/keliling Titik awal dan titik akhir merupakan titik yang sama. Untuk pengukuran sudut yang dilaksanakan sudut luar, maka kesalahan dapat dikontrol dari pengukuran karena jumlah sudut luar dari segi n harus sama dengan (2 n + 4) 90 0 atau (n + 2) 1800. Sedangkan untuk pengukuran sudut yang dilaksanakan sudut dalam, maka kesalahan pengukuran dapat dikontrol, dimana jumlah sudut dalam harus sama dengan (2 n – 4) 90 0 atau (n - 2) 1800. Dimana n adalah banyaknya sudut.

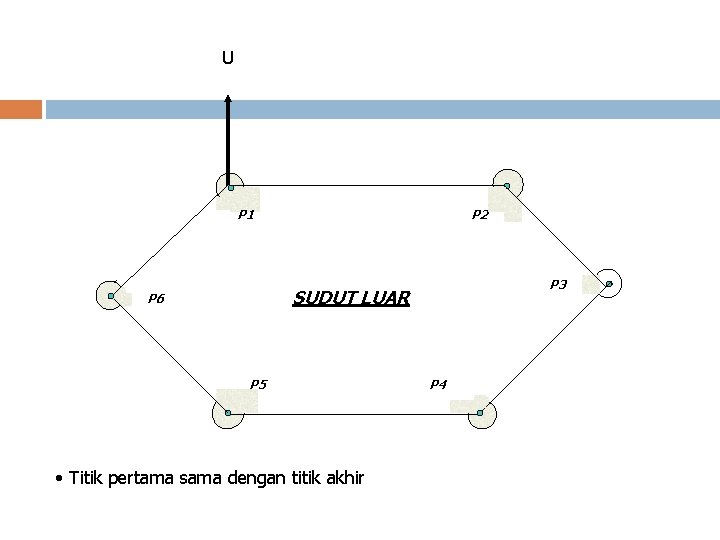
U P 1 P 2 P 3 SUDUT LUAR P 6 P 5 • Titik pertama sama dengan titik akhir P 4

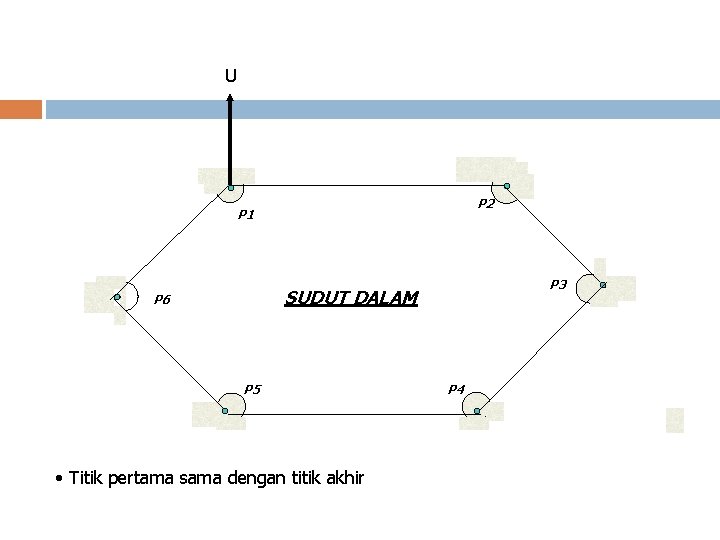
U P 2 P 1 P 3 SUDUT DALAM P 6 P 5 • Titik pertama sama dengan titik akhir P 4

Polygon Terbuka Titik pertama tidak sama dengan titik akhir v Polygon terbuka Bebas Ø Pada polygon ini dalam pengukuran sudut dan jarak tidak dapat dikontrol. Ø Dalam pengukuran ini tidak memerlukan ketentuan tentang letaknya dalam peta maka, tidak dapat memerlukan hitungan. Hitungan dalam pemetaannya, jadi cukup diukur panjang sisi dan besar sudutnya.

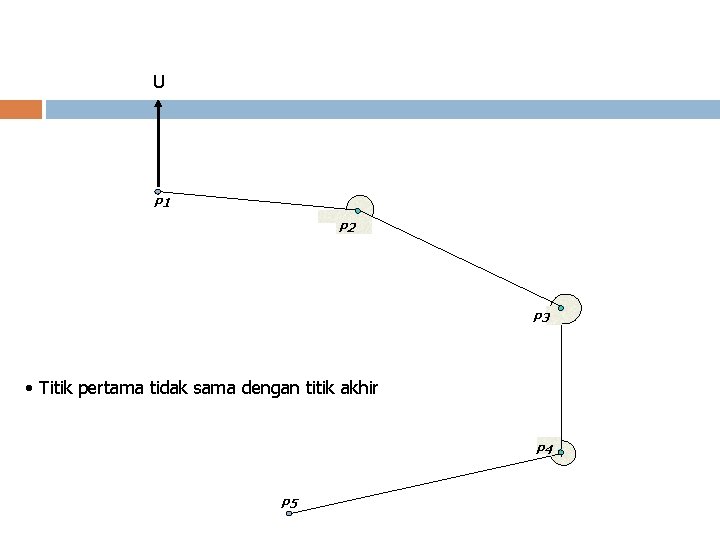
U P 1 P 2 P 3 • Titik pertama tidak sama dengan titik akhir P 4 P 5

Polygon Terbuka terikat sebagian Dalam pengukuran polygon terbuka terikat sebagian harus memenuhi syarat sebagai berikut : Satu titik harus diketahui koordinat. Satu sisi harus diketahui sudut jurusannya. Dua buah titik harus diketahui koordinatnya.

Maka untuk memenuhi syarat pertama harus memilih sebuah titik tetap (becnh mark) sebagai salah satu titik polygon yang sudah ada koordinatnya, dengan tujuan memudahkan perhitungan titik berikutnya. Sedangkan untuk memenuhi syarat kedua sebelum memulai pengukuran hendaknya theodolite diarahkan dahulu ke titik tetap lainnya agar dapat dihitung sudut jurusannya dari 2 buah titik yang berkoordinat. Untuk polygon jenis ini besar sudut dan jarak yang berukur tidak dapat dikoreksi secara analitis.

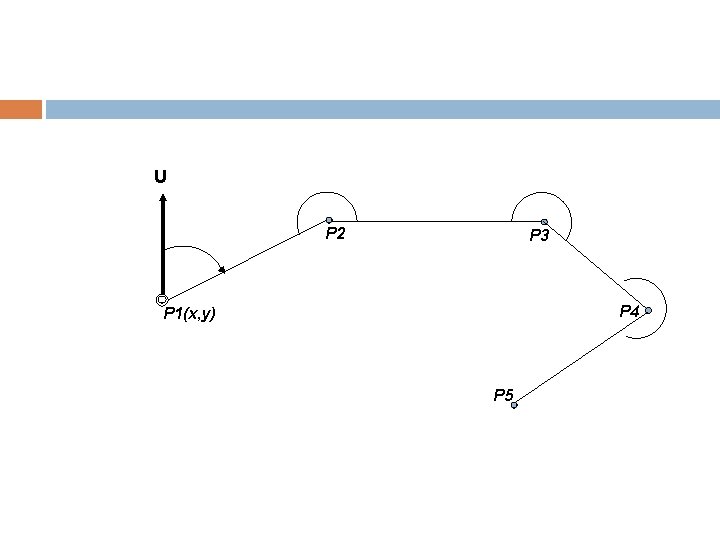
U P 2 P 3 P 4 P 1(x, y) P 5

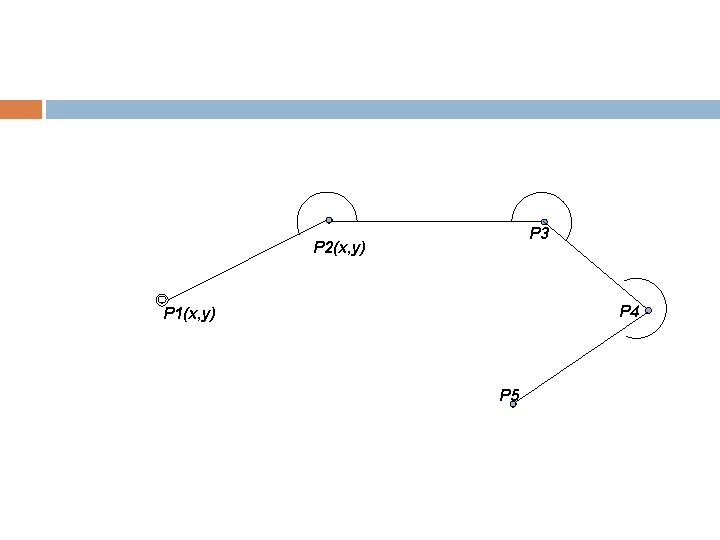
P 3 P 2(x, y) P 4 P 1(x, y) P 5

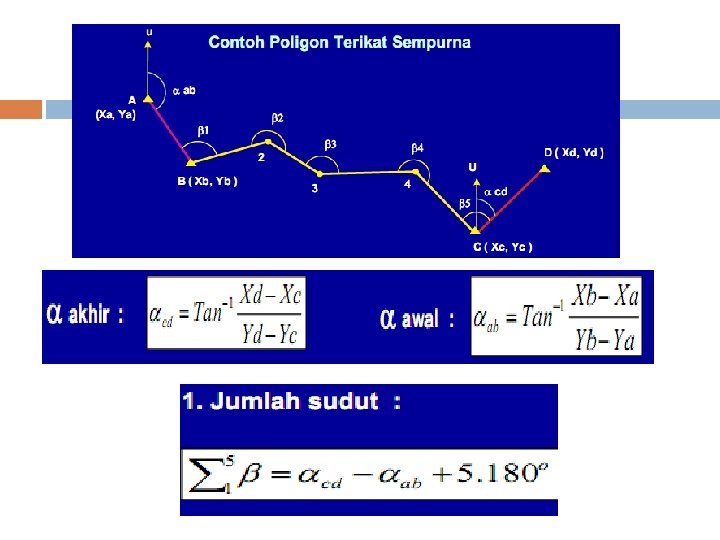
Polygon Terbuka Terikat Sempurna Mengukur polygon terbuka terikat sempurna, titik tetap awal dan titik tetap akhir harus sudah diketahui koordinat dan sudut jurusannya. Dari titik tetap itulah pengukuran diarahkan ketitik lain kemudian diukur sudut-sudut pada titik tersebut, sehingga mendapatkan sisi sudut jurusan yang berhubungan. Untuk jenis polygon ini sudut maupun jarak dapat dikoreksi secara analitis.

Koreksi sudut pada polygon macam ini adalah sebagai berikut : Pada pelaksanaan pengukuran yang didapat β sebelah kanan maka sudut dapat dikoreksi : β = α awal – α akhir + n. 180 Sedangkan bila pengukuran didapat β sebelah kiri maka sudut dapat dikoreksi : β = α akhir – α awal + n. 180 β = jumlah sudut terukur

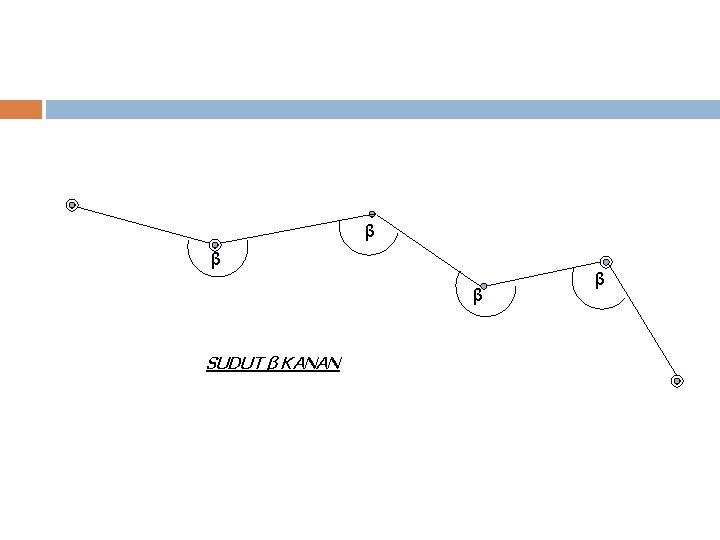
β β β SUDUT β KANAN β

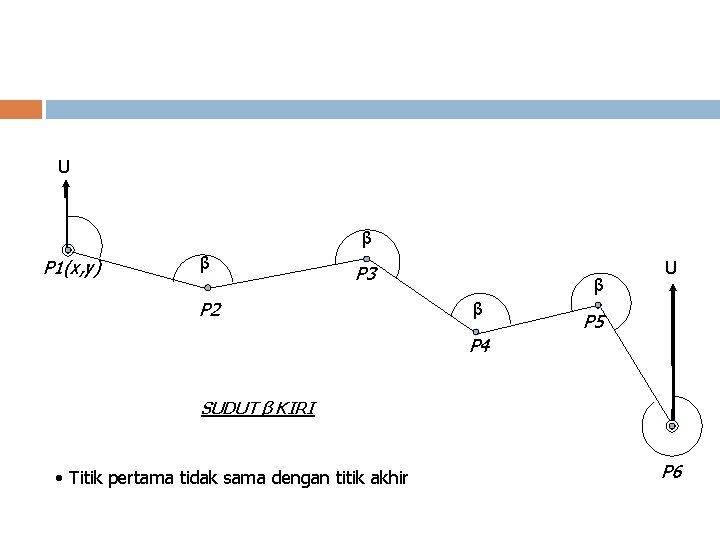
U β P 1(x, y) β P 3 P 2 β β U P 5 P 4 SUDUT β KIRI • Titik pertama tidak sama dengan titik akhir P 6

Syarat Pembuatan Titik Polygon a) Dalam menentukan jumlah titik berdasarkan pada fungsi polygon, harus b) Bentuk polygon diusahakan tidak terlalu banyak sudut. c) Jarak dari setiap titik – titik polygon diusahakan mendekati sama dan tidak terlalu pendek. d) Diusahakan tidak membentuk sudut lancip.

Syarat Penempatan Titik Polygon : Memudahkan untuk pelaksanaan pengukuran. Titik polygon harus dipilih pada daerah yang mudah dibidik secara langsung. Untuk memudahkan mencari titik polygon, usahakanlah titik polygon tersebut terletak dekat dengan obyek – obyek yang mudah dikenal, misalnya : pohon, tiang listrik dan lain – lain.

Pengukuran Sudut : Untuk mendapatkan pengukuran sudut yang teliti pengukuran dilaksanakan minimum 2 kali, yaitu : Pengukuran sudut datar posisi biasa ( posisi I ). Pengukuran sudut datar posisi luar biasa ( posisi II ) semakin banyak bacaan sudut yang diambil, maka kita dapat membandingkan bacaan sudut yang paling teliti ( lihat contoh tabel bacaan sudut datar dibawah ).

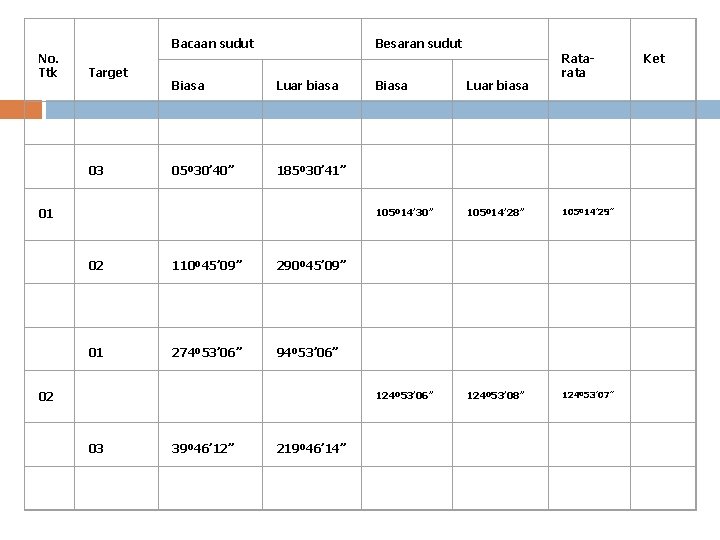
No. Ttk Bacaan sudut Target 03 Besaran sudut Biasa Luar biasa 05º 30’ 40” 185º 30’ 41” 01 02 110º 45’ 09” 290º 45’ 09” 01 274º 53’ 06” 94º 53’ 06” 02 03 39º 46’ 12” 219º 46’ 14” Ratarata Biasa Luar biasa 105º 14’ 30” 105º 14’ 28” 105º 14’ 29” 124º 53’ 06” 124º 53’ 08” 124º 53’ 07” Ket

Perhitungan Polygon Untuk perhitungan koordinat titik, dibutuhkan beberapa hal sebagai berikut : U d α A-P A Misalnya harus ditentukan letak titik P dari titik A yang telah diketahui koordinatnya, maka yang perlu ditentukan lebih dahulu adalah ARAH dari titik A ke titik P Untuk menentukan dimana letaknya titik P pada arah itu, diperlukan JARAK antara titik P ke titik A untuk diketahui, dimisalkan jarak sama dengan d Maka diarah AP dibuat jarak sebesar d sehingga letak titik P dan titik A dapat diketahui

Jadi untuk menentukan letak titik lainnya, diperlukan unsur -unsur : Arah/sudut jurusan/Azimuth Jarak. Suatu arah ditentukan dengan sudut yang : Dimulai dari arah utara geografis. Diputar searah dengan jalannya jarum jam. Diakhiri pada arah yang bersangkutan.

Dasar Perhitungan Poligon ü Contoh Perhitungan Poligon Terbuka Diketahui azimuth detail 1 ke detail 2 dan koordinat di detail 1, yaitu : X 1 = 1000 Y 1 = 1000 A 12 = 30˚ 01’ 30” ü Ditanyakan koordinat detail 2, 3, 4 dan 5

Dasar Perhitungan Poligon ü a. Penyelesaian : Hitung koordinat detail 2, jika d 12 = 30 m X 2 = X 1 + d 12 sin A 12 X 2 = 1000 + 30 sin 30˚ 01’ 30” X 2 = 1015. 0113 Y 2 = Y 1 + d 12 cos A 12 Y 2 = 1000 + 30 cos 30˚ 01’ 30” Y 2 = 1025. 9742

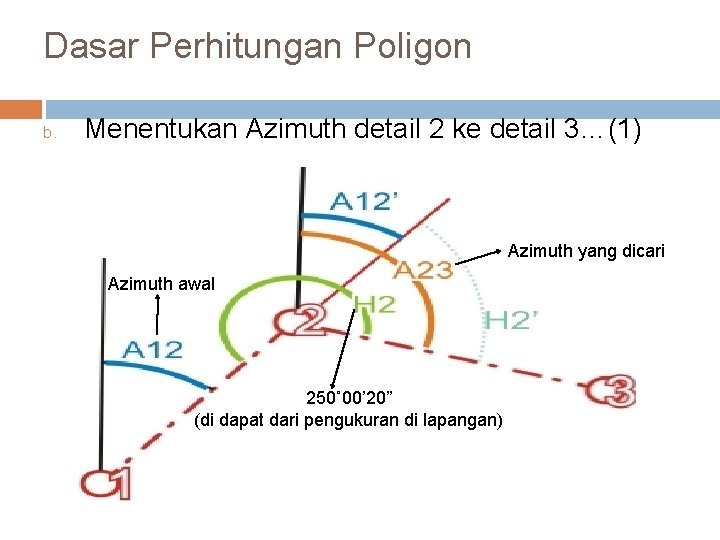
Dasar Perhitungan Poligon b. Menentukan Azimuth detail 2 ke detail 3…(1) Azimuth yang dicari Azimuth awal 250˚ 00’ 20” (di dapat dari pengukuran di lapangan)

Dasar Perhitungan Poligon b. Menentukan Azimuth detail 2 ke detail 3…(2) H 2’ = H 2 - 180˚, maka : A 23 = H 2’ + A 12’ [A = (H-180)+A’] A 23 = (H 2 - 180) + A 12 A 23 = (250˚ 00’ 20” - 180˚) + 30˚ 01’ 30” A 23 = 70˚ 00’ 20” + 30˚ 01’ 30” A 23 = 100˚ 01’ 50”

Dasar Perhitungan Poligon c. Hitung Koordinat detail 3, jika d 23 = 40 m X 3 = X 2 + d 23 sin A 23 X 3 = 1015. 0113 + 40 sin 100˚ 01’ 50” X 3 = 1054. 3999 Y 3 = Y 2 + d 23 sin A 23 Y 3 = 1025. 9742 + 40 cos 100˚ 01’ 50” Y 3 = 1019. 0073

Tugas Mandiri 4 Dari perhitungan poligon terbuka diatas, selesaikan untuk perhitungan koordinat detail 4 dan 5 dengan data lapangan sebagai berikut : ü H 3 = 175˚ 00’ 00” ü d 34 = 38, AB m ü H 4 = 170˚ 00’ 00” ü d 45 = 20, AB m Perhitungan dilampirkan dan hasil akhir perhitungan dibuat dalam Formulir Perhitungan Koordinat Poligon, utk koordinat detail 1 s/d 5.

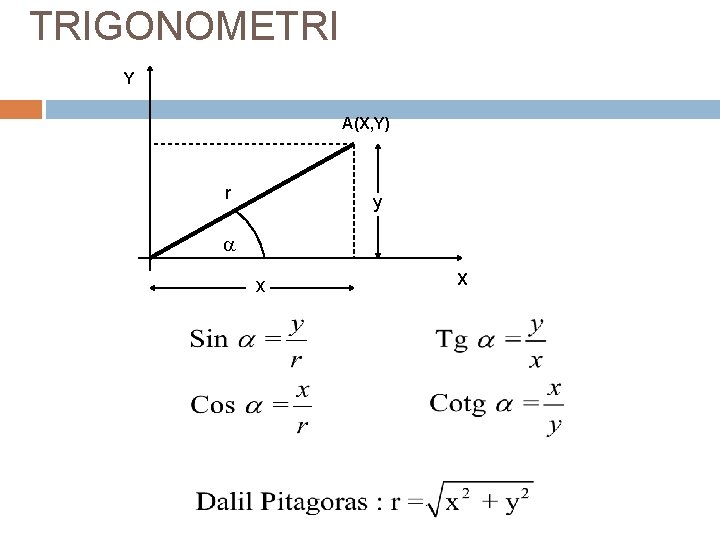
TRIGONOMETRI Y A(X, Y) r y a x X 42