PENGUKURAN DISPERSI KEMIRINGAN DAN KERUNCINGAN DISTRIBUSI DATA HOMOGEN

PENGUKURAN DISPERSI, KEMIRINGAN, DAN KERUNCINGAN DISTRIBUSI DATA

HOMOGEN DAN HETEROGEN DATA I. III. 50, 50, 50 30, 40, 50, 60, 70 20, 30, 50, 70, 80 Ketiga kelompok data mempunyai rata -rata hitung yang sama, yaitu :

DISPERSI DATA Ukuran penyebaran suatu kelompok data terhadap pusat data. Jenisnya : 1) Dispersi mutlak - Jangkauan (Range) - Simpangan Rata-rata (Mean Deviation) - Variansi (Variance) - Standar Deviasi (Standart Deviation) - Simpangan Kuartil (Quartile Deviation) 2) Dispersi relatif Koefisien Variasi (Coeficient of Variation)

1. JANGKAUAN r = nilai maksimum – nilai minimum Semakin kecil nilai r maka kualitas data akan semakin baik, sebaliknya semakin besar nilai r, maka kualitasnya semakin tidak baik.

2. SIMPANGAN RATA-RATA Jumlah nilai mutlak dari selisih semua nilai dengan nilai rata-rata dibagi dengan banyaknya data. Data tidak berkelompok : Data berkelompok :

SIMPANGAN RATA-RATA (lanjutan) Contoh : Interval Kelas X f 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Σf = 60 50, 92 37, 92 24, 92 11, 92 1, 08 14, 08 27, 08 152, 76 151, 68 99, 68 95, 36 12, 96 323, 84 162, 48 998, 76

3. VARIANSI Rata-rata kuadrat selisih dari semua nilai data terhadap nilai rata-rata hitung. Data tidak berkelompok : Data berkelompok :

4. STANDAR DEVIASI Akar pangkat dua dari Variansi. Disebut juga Simpangan Baku. Data tidak berkelompok : Data berkelompok :

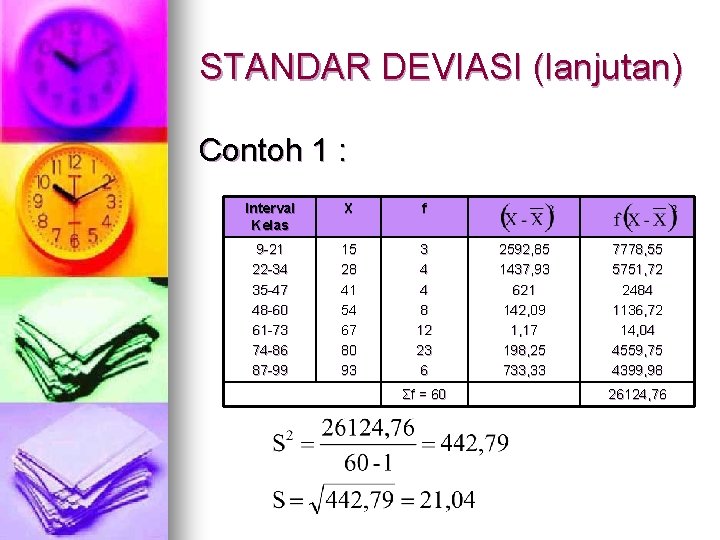
STANDAR DEVIASI (lanjutan) Contoh 1 : Interval Kelas X f 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Σf = 60 2592, 85 1437, 93 621 142, 09 1, 17 198, 25 733, 33 7778, 55 5751, 72 2484 1136, 72 14, 04 4559, 75 4399, 98 26124, 76

STANDAR DEVIASI (lanjutan) Menghitung Variansi dan Standar Deviasi juga dapat menggunakan Kode (U).

STANDAR DEVIASI (lanjutan) Contoh 2 : Interval Kelas X U f f. U 2 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 -3 -2 -1 0 1 2 3 3 4 4 8 12 23 6 -9 -8 -4 0 12 46 18 27 16 4 0 12 92 54 Σf = 60 Σf. U = 55 205

KEMIRINGAN DISTRIBUSI DATA Derajat atau ukuran dari ketidak simetrian suatu distribusi data. Ada 3 rumus : 1. Pearson 2. Momen 3. Bowley

1. RUMUS PEARSON

2. RUMUS MOMEN Data tidak berkelompok Data berkelompok

RUMUS MOMEN (lanjutan)

3. RUMUS BOWLEY 1. Jika Q 3 - Q 2 = Q 2 - Q 1 atau Q 3 + Q 1 - 2 Q 2 = 0 maka α = 0 dan distribusi datanya simetri 2. Jika Q 1 = Q 2 maka α = 1 dan distribusi datanya miring ke kanan 3. Jika Q 2 = Q 3 maka α = -1 dan distribusi datanya miring ke kiri

KERUNCINGAN DISTRIBUSI DATA Derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Disebut juga Kurtosis. Ada 3 jenis : 1. Leptokurtis, puncak relatif tinggi 2. Mesokurtis, puncaknya normal 3. Platikurtis, puncak rendah

KERUNCINGAN DISTRIBUSI DATA (lanjutan) Data tidak berkelompok Data berkelompok