Pengujian Hipotesis Sampel Besar Kelompok 13 AFIFAH NURUL

Pengujian Hipotesis Sampel Besar Kelompok 13 AFIFAH NURUL FITRI ANIAH FAUZIAH DINDA MALFIRA 201366174 201366161 201366083

Pengertian hipotesis Hipotesis pada dasarnya merupakan suatu jawaban sementara (proposisi) atau anggapan yang mungkin benar dan sering digunakan sebagai dasar pembuatan keputusan atau pemecahan persoalan untuk dasar penelitian lebih lanjut. Hipotesis adalah suatu pernyataan mengenai nilai suatu parameter populasi yang dimaksudkan untuk pengujian dan berguna untuk pengambilan keputusan

Hipotesis yang baik a. Menyatakan hubungan b. Sesuai dengan fakta c. Sederhana dan dapat di uji d. Dapat menerangkan fakta dengan baik

Pengujian hipotesis Prosedur yang didasarkan pada bukti sampel yang dipakai untuk menentukan apakah hipotesis merupakan suatu pernyataan yang wajar dan oleh karenanya tidak ditolak, atau hipotesis itu tidak wajar dan oleh karena itu harus ditolak

Prosedur pengujian hipotesis Langkah 1 Merumuskan Hipotesis (H 0 dan H 1) Langkah 2 Menentukan Taraf Nyata (Probabilitas menolak hipotesis) Langkah 3 Menentukan Uji Statistik (Alat uji statistik / uji Z, t, F, X 2, dll) Langkah 4 Menentukan Daerah Keputusan(Daerah dimana hipotesis nol diterima/ditolak) Langkah 5 Mengambil Keputusan Menerima H 0 Menolak H 0 Menerima H 1

• Langkah 1 Merumuskan Hipotesis • Hipotesis Alternatif (H 1) • Hipotesis Nol (H 0) suatu pernyataan mengenai nilai parameter populasi suatu pernyataan yang diterima jika data sampel memberikan cukup bukti bahwa hipotesis nol adalah salah

• Langkah 2 Menentukan Taraf Nyata Taraf nyata adalah probabilitas menolak hipotesis nol apabila hipotesis nol itu benar v Dilambangkan dengan α v dimana α = 1 – C Semakin kecil taraf nyata (α) atau semakin besar tingkat keyakinan (C), maka semakin baik.

• Langkah 3 Menentukan Uji Statistik Uji statistik adalah suatu nilai yang diperoleh dari sampel dan digunakan untuk memutuskan apakah akan menerima atau menolak hipotesis. Uji statistik : Uji Z, uji t, uji F, uji Chi-kuadrat, dll Dimana : Z : Nilai Z x : rata-rata hitung sampel µ : Rata-rata hitung populasi Sx : Standar error sampel sx = σ/√n (populasi diketahui) sx = s/√n (populasi tidak diketahui) Z=

• Langkah 4 Menentukan Daerah Keputusan Daerah keputusan : Merupakan pernyataan mengenai kondisi dimana hipotesa nol ditolak atau diterima. • Menggunakan uji Z; - misal Probabilitas 0, 5 dan taraf nyata 5% Pengujian satu arah : Probabilitas = 0, 5 – 0, 05 = 0, 4500 (tentukan nilai Z dengan probabilitas 0, 4500) Z = 1, 65

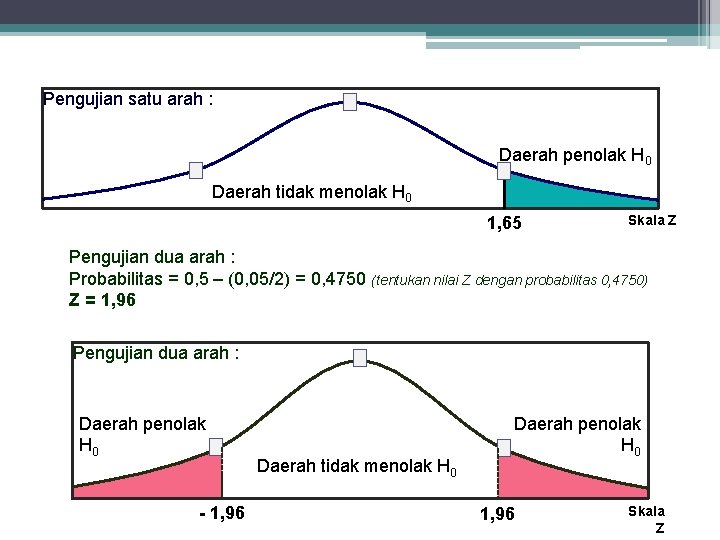
Pengujian satu arah : Daerah penolak H 0 Daerah tidak menolak H 0 1, 65 Skala Z Pengujian dua arah : Probabilitas = 0, 5 – (0, 05/2) = 0, 4750 (tentukan nilai Z dengan probabilitas 0, 4750) Z = 1, 96 Pengujian dua arah : Daerah penolak H 0 - 1, 96 Daerah tidak menolak H 0 Daerah penolak H 0 1, 96 Skala Z

• Langkah 5 Mengambil keputusan Dengan Uji Z Tentukan nilai Z dan lihat terletak didaerah mana pada daerah pengujian

• • • #1 #2 #3 #4 #5 Merumuskan Hipotesis Menentukan Taraf Nyata Menentukan Uji Statistik Menentukan Daerah Keputusan Mengambil Keputusan

UJI SIGNIFIKAN Satu Arah & Dua Arah • One tail test (kiri) : Pengujian satu arah pihak kiri dimana H 0 ≥ dan H₁< • One tail test (kanan) : Pengujian satu arah pihak kanan dimana H 0 ≤ dan H₁ > • Two tail test : Pengujian dua arah dimana H 0 = dan H₁ ≠.

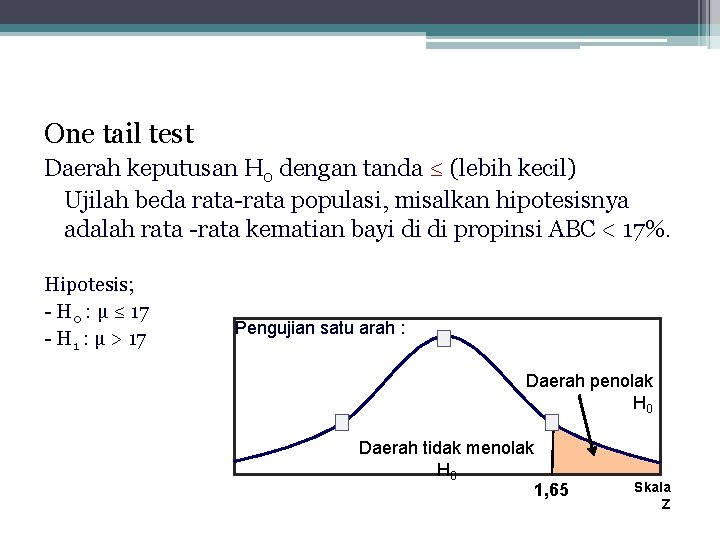
One tail test Daerah keputusan H 0 dengan tanda ≤ (lebih kecil) Ujilah beda rata-rata populasi, misalkan hipotesisnya adalah rata -rata kematian bayi di di propinsi ABC < 17%. Hipotesis; - H 0 : µ ≤ 17 - H 1 : µ > 17 Pengujian satu arah : Daerah penolak H 0 Daerah tidak menolak H 0 1, 65 Skala Z

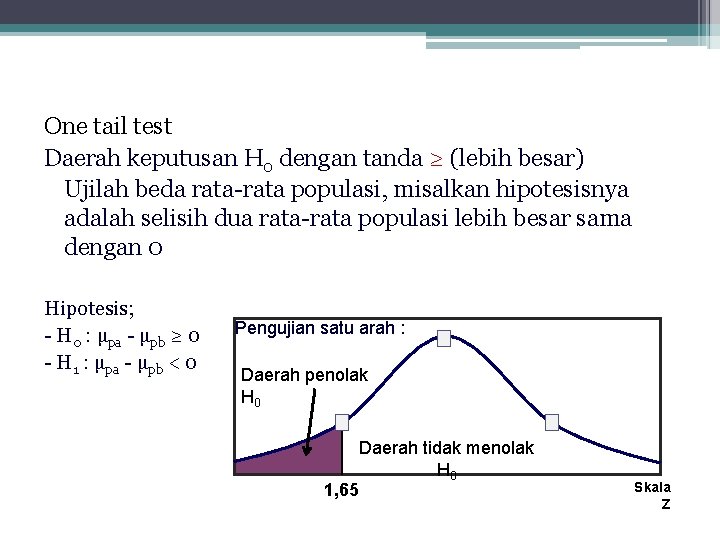
One tail test Daerah keputusan H 0 dengan tanda ≥ (lebih besar) Ujilah beda rata-rata populasi, misalkan hipotesisnya adalah selisih dua rata-rata populasi lebih besar sama dengan 0 Hipotesis; - H 0 : µpa - µpb ≥ 0 - H 1 : µpa - µpb < 0 Pengujian satu arah : Daerah penolak H 0 Daerah tidak menolak H 0 1, 65 Skala Z

Two tail test Ujilah nilai rata-rata = 17%, maka hipotesisnya ; H 0 : µ = 17 - H 1 : µ ± 17 Misalnya dengan menggunakan taraf nyata α = 5% Maka luas daerah penerimaaan H 0 = 0, 5 – (0, 05/2) = 0, 4 (tentukan nilai Z) Z = 1, 96 Pengujian dua arah : Tidak menolak H 0 Penolak H 0 - 1, 96 Penolak H 0 1, 96 Skala Z

Menguji Hipotesis Rata-rata dan Proposi Sampel Besar 3 hal terkait 1)Menguji Hipotesis Rata-rata Sampel Besar (5 langkah) 2)Objek Pengujian Rata-rata Sampel besar & Proporsi Sampel Besar 3)Ukuran Sampel (sampel berukuran 30 atau lebih)

Menguji Hipotesis Rata-rata Sampel Besar Contoh soal : Suatu pabrik suatu merek Good Milk melakukan pengecekan terhadap produk mereka, apakah rata-rata berat bersih 1 kaleng susu bubuk yang diproduksi dan dipasarkan masih tetap 400 g atau sudah lebih kecil dari itu. Dari data sebelumnya diketahui bahwa simpangan baku bersih per kaleng sama dengan 125 g. Dari sampel 50 kaleng yang diteliti, diperoleh rata-rata berat bersih 375 g. Dapatkah diterima bahwa berat bersih rata-rata yang dipasarkan tetap 400 g ? Ujilah dengan taraf nyata 5% !

Diketahui : n = 50 (jml populasi) X =375 (rata-rata sampel) σ =125 (simpangan baku) µ =400 (rata-rata populasi) Jawab : a. Formulasi hipotesisnya : H₀ : µ = 400 H₁ : µ ≠ 400 b. Taraf nyata dan nilai tabelnya : α = 5% =0, 05 • Probabilitas = 0, 5 – (0, 05/2) = 0, 4750 (tentukan nilai Z dengan probabilitas 0, 4750) • Z = 1, 96

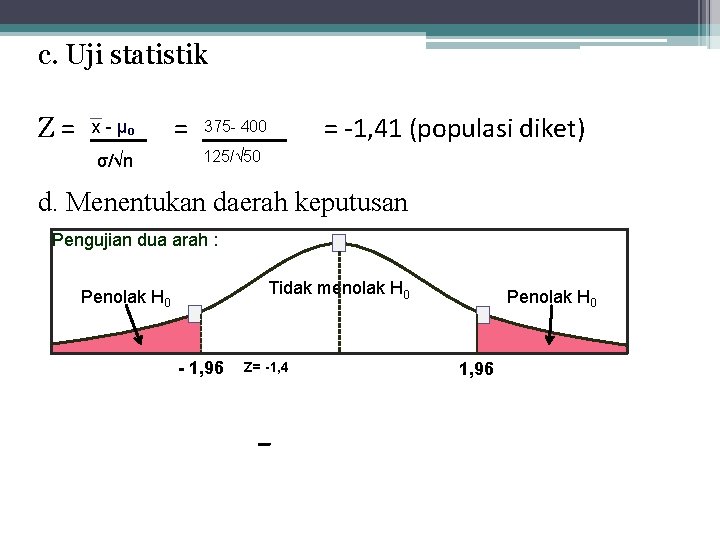
c. Uji statistik Z= x - µ₀ σ/√n = = -1, 41 (populasi diket) 375 - 400 125/√ 50 d. Menentukan daerah keputusan Pengujian dua arah : Tidak menolak H 0 Penolak H 0 - 1, 96 Z= -1, 4 Penolak H 0 1, 96

e. Kesimpulan karena Z = -1, 41 berada di daerah tidak menolak H₀ maka H₀ di terima.

Menguji Hipotesis Proporsi Sampel Besar - Proses sama dengan pengujian hipotesis rata-rata - Perbedaan pada rumus uji Z; Z = p-P n di mana : Z : Nilai uji Z p : Proporsi sampel P : Proporsi populasi n : Jumlah sampel

Contoh soal : Perusahaan pembiayaan (multifinance) di lndonesia relatil kalah perkembangannya dengan perusahaan reksa dana. Pada tahun 2008 aset total mencapai Rp 27 triliun untuk 116 perusahaan, atau aset perusahaan hanya Rp 232 miliar bandingkan dengan reksa dana di mana aset total mencapai 150 triliun untuk 128 perusahaan, atau setiap perusahaan mempunyai aset 1, 17 triliun. Menurut majalah lnvestor, Juni 2008, walaupun perusahaan pembiayaan relatif kurang berkembang, ternyata lebih dari 50% merupakan perusahaan yang sehat. Untuk meneliti lebih lanjut tentang perkembangan perusahaan pembiayaan diambil sebanyak 43 perusahaan sebagai sampel. Hasil penelitian menunjukkan bahwa 47% sehat. Dengan menggunakan taraf nyata 1% dan probabilitasnya 0, 5 apakah penemuan majalah investor tersebut cukup bukti ?

Diketahui : P = 50%= 0, 5 n = 43 α = 1% = 0, 01 p = 47% = 0, 47 Jawab: 1. Perumusan hipotesis H 0 : P ≥ 0, 5 H 1 : P < 0, 5 Tanda persamaan pada hipotesis adalah ≥ dan <, ini merupakan tanda untuk uji satu arah, di mana daerah penolakan hipotesis nol berada pada ekor kiri. 2. Menentukan taraf nyata Probabilitas untuk nilai kritis Z = 0, 5 - 0, 01 = 0, 49 nilai kritis Z=2, 33 karena berada disebelah ekor kiri, maka tandanya negatif menjadi -2, 33. 3. Melakukan uji statistik Z= p-P n = 0, 47 – 0, 50 43 = -0, 03 0, 076 = -0, 39

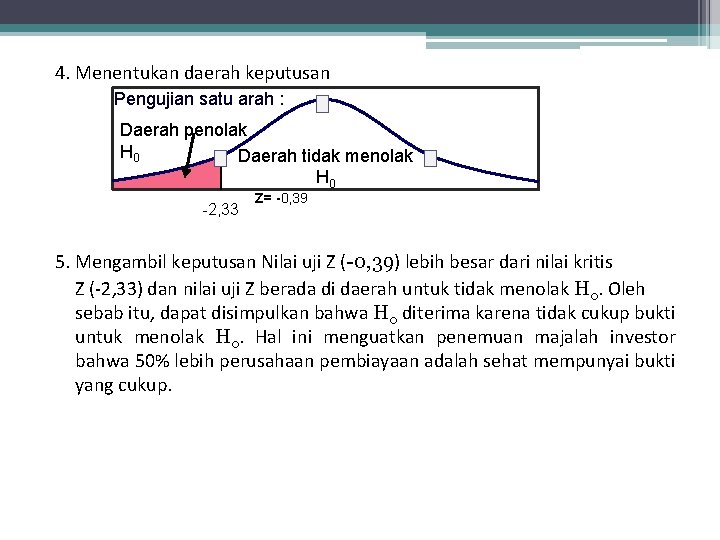
4. Menentukan daerah keputusan Pengujian satu arah : Daerah penolak H 0 Daerah tidak menolak H 0 -2, 33 Z= -0, 39 5. Mengambil keputusan Nilai uji Z (-0, 39) lebih besar dari nilai kritis Z (-2, 33) dan nilai uji Z berada di daerah untuk tidak menolak H 0. Oleh sebab itu, dapat disimpulkan bahwa H 0 diterima karena tidak cukup bukti untuk menolak H 0. Hal ini menguatkan penemuan majalah investor bahwa 50% lebih perusahaan pembiayaan adalah sehat mempunyai bukti yang cukup.

Menguji Hipotesis Selisih Rata-rata dan Proposi Sampel Besar • Bertujuan untuk menetapkan apakah dua rata-rata atau proporsi dua populasi sama atau tidak. - Apakah hasil diet OCD lebih baik dari diet puasa konvensional ? - Apakah kinerja obat bius A lebih cepat dari B ? Standar deviasi = di mana : : Sandar deviasi selisih dua populasi : Standar deviasi populasi 1 : Standar deviasi populasi 2 N 1 : Jumlah sampel pada populasi 1 N 2 : Jumlah sampel pada populasi 2

Nilai uji statistik Z = Sx 1 -x 2 di mana : Z : Nilai uji statistik Sx 1 -x 2 : Selisih dua rata-rata hitung sampel 1 dan sampel 2 : Selisih dua rata-rata hitung populasi 1 dan populasi 2 : Standar deviasi selisih dua populasi

Standar deviasi selisih dua sampel Sx 1 -x 2 = √ S 21 / n 1 + S 22 / n 2 di mana : Sx 1 -x 2 : Standar deviasi selisih dua proporsi populasi S 1 S 2 n 1 n 2 : Standar deviasi sampel 1 : Standar deviasi sampel 2 : Jumlah sampel pada populasi 1 : Jumlah sampel pada populasi 2

Selisih rata-rata dan proporsi sampel besar Contoh Soal : Seorang investor ingin mengetahui apakah hasil investasi pada reksa dan deposito perbankan sama. Untuk keperluan tersebut dipilih 36 perusahaan reksa dan hasil rata- rata mencapai 13, 17% untuk reksa dana pendapatan tetap dengan standar deviasi 2, 09%. Pada 49 perbankan diketahui bahwa suku bunga rata-rata 7, 55% dan standar deviasi 1, 09%. Dengan taraf nyata 5%, tentukan apakah rata hasil investasi di reksa dan perbankan sama?

Diketahui: *taraf nyata (α) = 5% = 0, 05 * investasi reksa dana X₁ = 13, 17% S₁ = 2, 09% n₁ = 36 * deposito bank X₂ = 7, 55% S₂ = 1, 09% n₂ = 49 Jawab: 1. Merumuskan hipotesis Hal ini dilakukan dengan menguji pernyataan bahwa rata-rata hasil investasi reksa dana (µ₁) dan perbankan (µ₂) sama yang dinyatakan µ₁ = µ ₂ atau µ ₁ - µ ₂ = 0. Hipotesis tersebut dapat dirumuskan sebagai berikut: H₀ : µ ₁ - µ ₂ = 0 H₁: µ₁-µ₂≠ 0 Tanda = dan ≠ pada perumusan hipotesis tersebut menunjukkan adanya pengujian dua arah.

2. Menentukan taraf nyata probabilitas daerah keputusan H₀ yaitu, Zα/₂ = α/2 = 0, 05/2 = 0, 025 probabilitas untuk nilai kritis Z = 0, 5 - 0, 025 = 0, 4750 maka nilai kritis Z pada tabel adalah 1, 96 3. Melakukan uji statistik dengan menggunakan rumus Z untuk selisih rata- rata Sx 1 -x 2 = Z= √ = S 21 / n 1 + S 22 / n 2 Sx 1 -x 2 √ 2, 092/36 + 1, 092/49 = 0, 40 - 0= 14, 05 = 0, 40

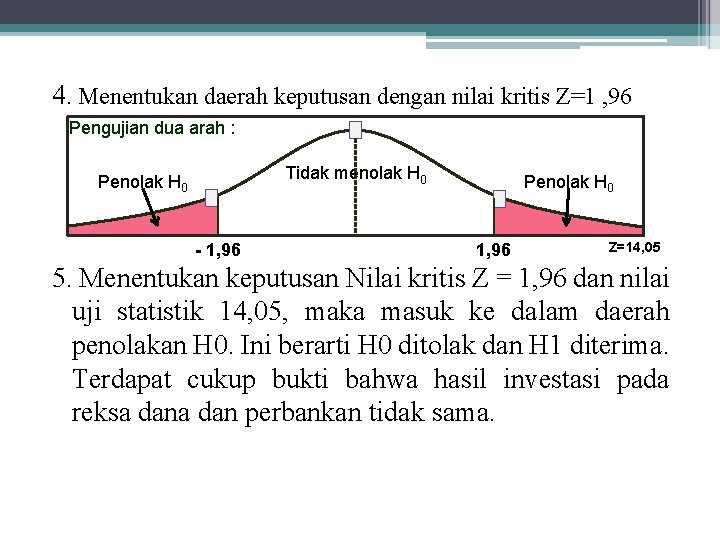
4. Menentukan daerah keputusan dengan nilai kritis Z=1 , 96 Pengujian dua arah : Tidak menolak H 0 Penolak H 0 - 1, 96 Penolak H 0 1, 96 Z=14, 05 5. Menentukan keputusan Nilai kritis Z = 1, 96 dan nilai uji statistik 14, 05, maka masuk ke dalam daerah penolakan H 0. Ini berarti H 0 ditolak dan H 1 diterima. Terdapat cukup bukti bahwa hasil investasi pada reksa dan perbankan tidak sama.

Menguji Hipotesis Selisih Proporsi Sampel Besar Standar Deviasi Proporsi Populasi: Sp 1 -p 2 = √ [P (1 -P )]/n 1 1 1 + [P 2(1 -P 2)]/n 2 di mana : Sp 1 -p 2 : Standar deviasi selisih dua proporsi populasi P 1 P 2 n 1 n 2 : Proporsi populasi 1 : Proporsi populasi 2 : Jumlah sampel pada populasi 1 : Jumlah sampel pada populasi 2

Nilai uji statistikmp Z= (p 1 – p 2)(P 1 – P 2) Sp 1 -p 2 di mana : Z : Nilai uji statistik p 1 – p 2 : Selisih dua proporsi sampel 1 dan sampel 2 P 1 – P 2 : Selisih dua proporsi populasi 1 dan populasi 2 Sp 1 -p 2 : Standar deviasi selisih dua proporsi populasi Standar Deviasi selisih dua sampel Sp 1 -p 2 = √ [P(1 -p)]/(n -1) + [P(1 -P)]/(n -1) 1 2 Standar deviasi populasi tidak diketahui Dimana P = (x 1 -x 2)/(n 1+n 2) ; - x 1 dan x 2 adalah kejadian sukses pada sampel 1 dan 2

Contoh soal : Majalah SWA edisi juni 2008 membahas tentang gelombang baru bisnis music indonesia. Fenomena yang sangat mencolok adalah grup samsons yang mampu menciptakan lagu kenangan terindah dan di download lebih dari 3 juta pelanggan hp. Acara musik lokal saat ini juga sudah dapat menggeser acara musik barat. Menurut majalah ini, rating acara musik dibeberapa TV seperti RCTI dan SCTV mencapai 35, artinya pada waktu yang sama ditonton 35 juta orang. Sebuah perusahaan kosmetik remaja ingin memasang iklan pada acara musik tersebut dan ingin menegtahui apakah proporsi remaja dan dewasa sama. Untuk mengetahui hasil tersebut dicari responden per telepon sebanyak 300 remaja dan 150 orang menonton acara musik lokal sedangkan, responden dewasa sebanyak 400 orang dan 350 menonton acara musik lokal. Dengan traf nyata 5% ujilah apakah proporsi remaja dan dewasa sama dalam menonton acara musik lokal tersebut ?

Jawab : 1. Merumuskan hipotesis H 0 : P 1 – P 2 = 0 H 1 : P 1 – P 2 ≠ 5 Tanda = dan ≠ pada perumusan hipotesis tersebut menunjukkan adanya pengujian dua arah. ilitas nyata 2. taraf Menentukan keputusan H₀ yaitu, Zα/₂ = α/2 = 0, 05/2 = 0, 025 probabilitas untuk nilai kritis Z = 0, 5 - 0, 025 = 0, 4750 maka nilai kritis Z pada tabel adalah 1, 96

3. Melakukan uji statistik dengan menggunakan rumus Z untuk selisih 2 proporsi sampel. dik : X₁ = 150 n₁ = 300 p 1 = 150/300 = 0, 50 X₂ = 350 n₂ = 400 p 2 = 350/400 = 0, 875 p 1 – p 2 = 0, 50 -0, 875 = -0, 375 P = (x 1 -x 2)/(n 1+n 2) = (150+350) / (300+400) = 0, 71 Nilai standar error selisih dua proporsi : Sp 1 -p 2 = = √ [P(1 -p)]/(n -1) + [P(1 -P)]/(n -1) 1 2 √ [0, 71(1 -0, 71)]/(300 -1) + [0, 71(1 -0, 71)]/(400 -1) = 0, 035

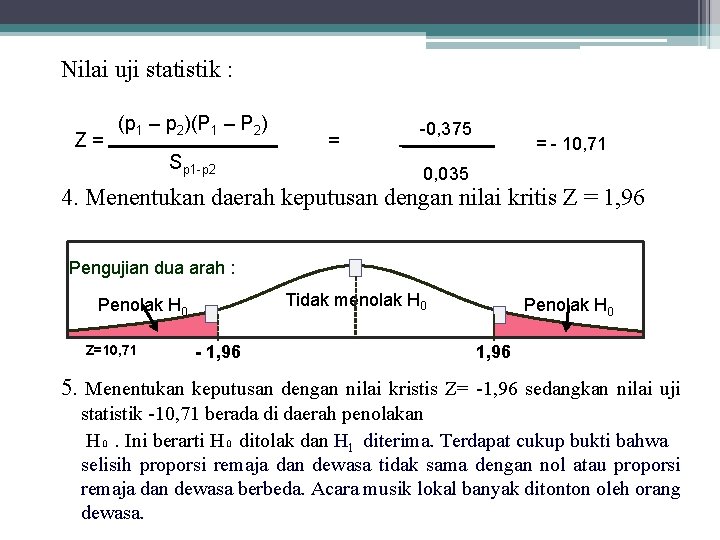
Nilai uji statistik : Z= (p 1 – p 2)(P 1 – P 2) Sp 1 -p 2 = -0, 375 = - 10, 71 0, 035 4. Menentukan daerah keputusan dengan nilai kritis Z = 1, 96 Pengujian dua arah : Tidak menolak H 0 Penolak H 0 Z=10, 71 - 1, 96 Penolak H 0 1, 96 5. Menentukan keputusan dengan nilai kristis Z= -1, 96 sedangkan nilai uji statistik -10, 71 berada di daerah penolakan H₀. Ini berarti H₀ ditolak dan H 1 diterima. Terdapat cukup bukti bahwa selisih proporsi remaja dan dewasa tidak sama dengan nol atau proporsi remaja dan dewasa berbeda. Acara musik lokal banyak ditonton oleh orang dewasa.

Jenis Kesalahan I dan II Kesalahan jenis I : apabila keputusan menolak H 0, padahal seharusnya H 0 benar. Kesalahan jenis II : apabila keputusan menerima H 0, padahal seharusnya H 0 salah. Situasi Keputusan H 0 Benar H 0 Salah Terima H 0 Keputusan tepat (1 – α) Kesalahan jenis 2 (β) Tolak H 0 Kesalahan jenis 1 (α) Keputusan tepat (1 – β)

TERIMA KASIH