Pengujian Hipotesis Deskriptif Hipotesis Deskriptif q Hipotesis deskriptif

Pengujian Hipotesis Deskriptif

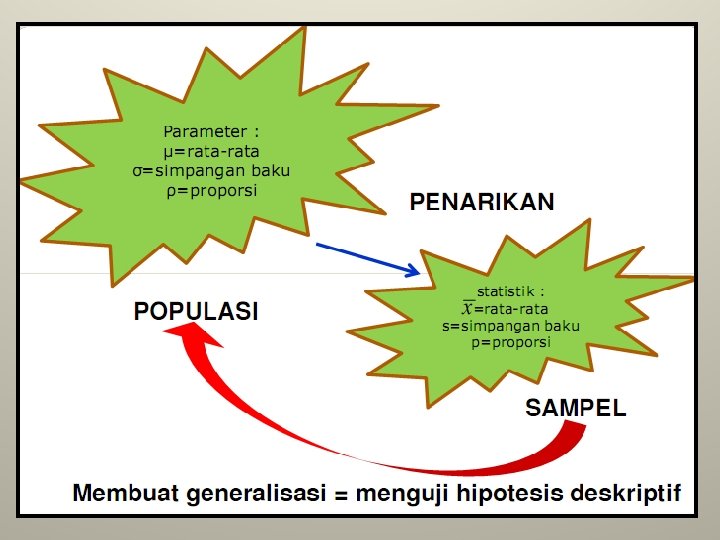
Hipotesis Deskriptif q Hipotesis deskriptif adalah dugaan tentang nilai suatu variabel mandiri, tidak membuat perbandingan atau hubungan q Dalam penelitian hanya bertujuan untuk menjelaskan satu variabel saja atau lebih dikenal dengan penelitian univariat. q Merupakan proses pengujian generalisasi hasil penelitian yg didasarkan pada 1 sampel q Kesimpulan yg akan dihasilkan adalah apakah hipotesis yg diuji dapat digeneralisasikan atau tidak.

Statistik Uji Hipotesis Deskriptif (1 sampel) Macam Data Nominal 1. Test Binomial 2. Chi Kuadrat (1 sampel) Nominal Ordinal Bentuk Hipotesis Deskriptif (satu variabel) Komparatif (dua sampel) Komparatif (lebih dari 2 sampel) Related Independen Binomial 2 One Sample Mc Nemar Fisher Exact Probability 2 for k sample Contingency Coefficient C 2 Two Sample Cochran Q Median test Mann. Whitney U test Friedman Two Way. Anova Median Extension Spearman Rank Correlation Run Test Data Ordinal 1. Run test Sign test Wilcoxon matched parts Kruskal. Wallis One Way Anova Kolmogorov Simrnov Data interval/ratio 1. t-test (1 sampel) Asosiatif (hubungan) Kendall Tau Wald. Woldfowitz Interval Rasio T Test* T-test of* Related T-test of* independen t One-Way Anova* Two Way Anova* Pearson Product Moment * Partial Correlation* Multiple Correlation*

t-test • Rumus t hitung

Langkah-langkah Pengujian Hipotesis Deskriptif 1) Menghitung rata-rata data 2) Menghitung simpangan baku 3) Menghitung harga t hitung 4) Melihat harga t tabel Atau untuk menguji hipotesisnya bisa dengan gambar lonceng (distribusi normal) 1) Menggambarkan kurva lonceng 2) Meletakkan kedudukan t hitung dan t tabel dalam kurva yang telah dibuat 3) Membuat keputusan pengujian hipotesis Arah Pengujian Hipotesis Macam pengujian hipotesis deskriptif: 1. Uji dua pihak (two tail test) 2. Uji satu pihak (one tail test) Uji satu pihak ada dua : • uji pihak kanan • uji pihak kiri. Jenis uji mana yang digunakan tergantung pada bunyi hipotesis

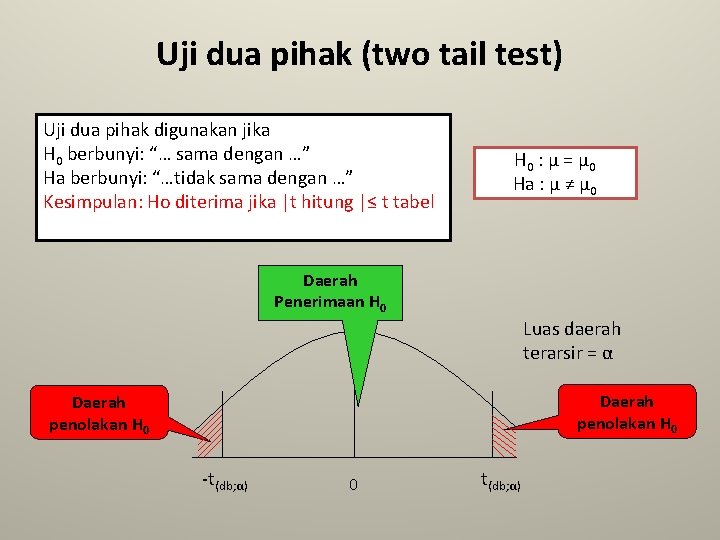
Uji dua pihak (two tail test) Uji dua pihak digunakan jika H 0 berbunyi: “… sama dengan …” Ha berbunyi: “…tidak sama dengan …” Kesimpulan: Ho diterima jika |t hitung |≤ t tabel H 0 : μ = μ 0 Ha : μ ≠ μ 0 Daerah Penerimaan H 0 Luas daerah terarsir = α Daerah penolakan H 0 -t(db; α) 0 t(db; α)

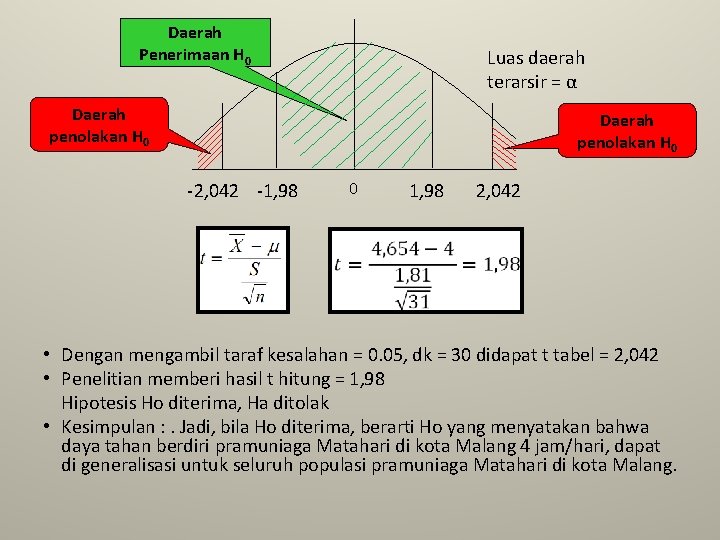
Contoh Uji Dua Pihak: Telah dilakukan pengumpulan data untuk menguji hipotesis yang menyatakan bahwa “daya tahan berdiri pramuniaga toko Matahari di kota Malang adalah 4 jam/hari” sebagai berikut: Penyelesaian : • H 0 : μ = 4 jam/hari • Ha : μ ≠ 4 jam/hari • N =31 dk =31 -1=30 • S = 1, 81 • µo = 4 jam/hari

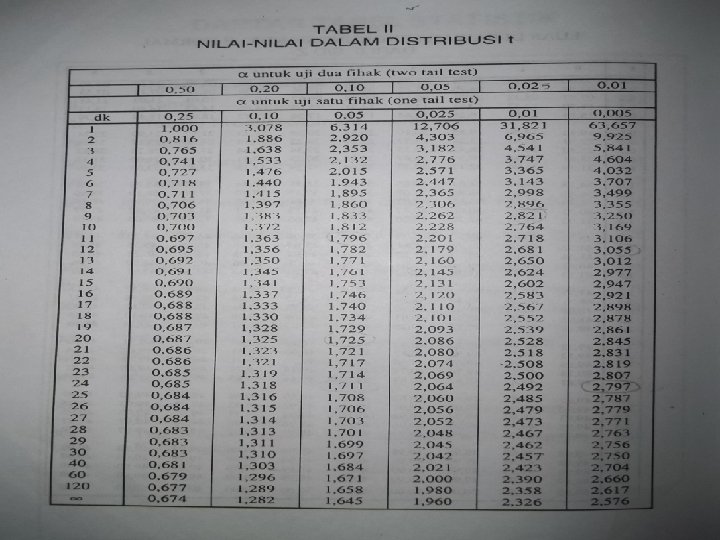
Daerah Penerimaan H 0 Luas daerah terarsir = α Daerah penolakan H 0 -2, 042 -1, 98 0 1, 98 2, 042 • Dengan mengambil taraf kesalahan = 0. 05, dk = 30 didapat t tabel = 2, 042 • Penelitian memberi hasil t hitung = 1, 98 Hipotesis Ho diterima, Ha ditolak • Kesimpulan : . Jadi, bila Ho diterima, berarti Ho yang menyatakan bahwa daya tahan berdiri pramuniaga Matahari di kota Malang 4 jam/hari, dapat di generalisasi untuk seluruh populasi pramuniaga Matahari di kota Malang.

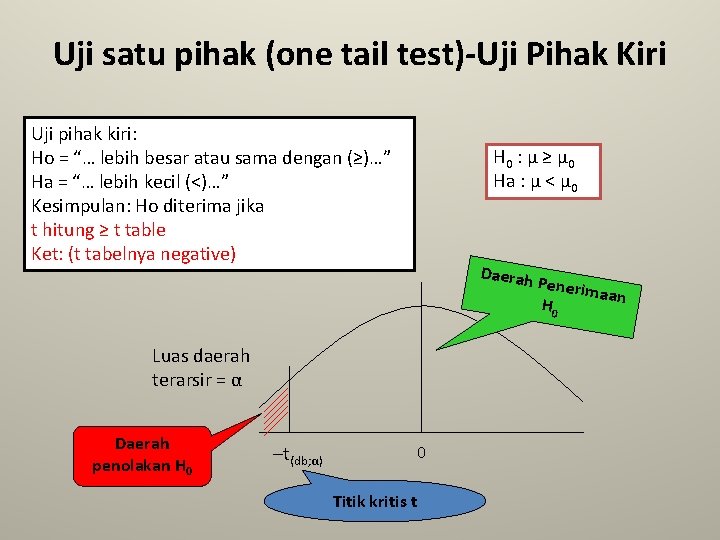
Uji satu pihak (one tail test)-Uji Pihak Kiri Uji pihak kiri: Ho = “… lebih besar atau sama dengan (≥)…” Ha = “… lebih kecil (<)…” Kesimpulan: Ho diterima jika t hitung ≥ t table Ket: (t tabelnya negative) H 0 : μ ≥ μ 0 Ha : μ < μ 0 Daerah Luas daerah terarsir = α Daerah penolakan H 0 –t(db; α) 0 Titik kritis t Penerim aan H 0

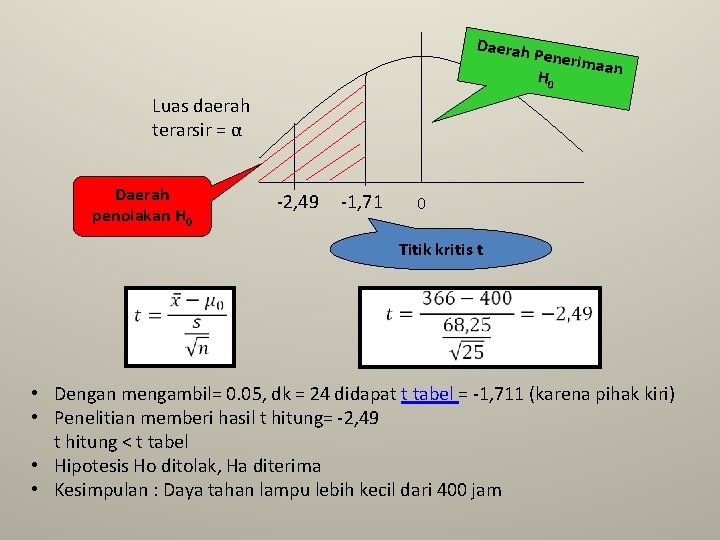
Suatu perusahaan pijar merk laser, menyatakan bahwa daya tahan lampu yang dibuat paling kecil 400 jam. Pengumpulan data untuk menguji hipotesis yang menyatakan bahwa “daya tahan lampu yang dibuat paling kecil 400 jam” sebagai berikut: 450 390 400 480 500 350 400 340 300 375 425 400 425 390 350 360 300 200 380 345 340 250 400 S=68, 25 a. Tuliskan hipotesis penelitian dan statistiknya b. Gunakan uji t untuk menguji hipotesis itu c. Tuliskan kesimpulan dan gambarnya.

Daerah Penerim aan H 0 Luas daerah terarsir = α Daerah penolakan H 0 -2, 49 -1, 71 0 Titik kritis t • Dengan mengambil= 0. 05, dk = 24 didapat t tabel = -1, 711 (karena pihak kiri) • Penelitian memberi hasil t hitung= -2, 49 t hitung < t tabel • Hipotesis Ho ditolak, Ha diterima • Kesimpulan : Daya tahan lampu lebih kecil dari 400 jam

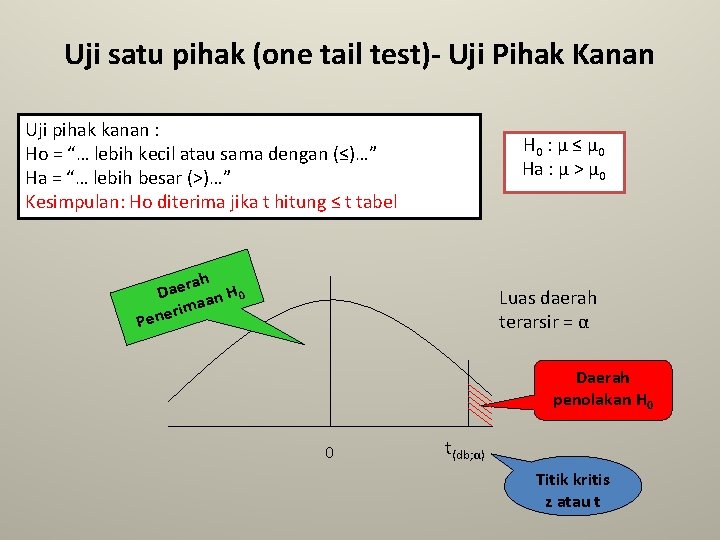
Uji satu pihak (one tail test)- Uji Pihak Kanan Uji pihak kanan : Ho = “… lebih kecil atau sama dengan (≤)…” Ha = “… lebih besar (>)…” Kesimpulan: Ho diterima jika t hitung ≤ t tabel H 0 : μ ≤ μ 0 Ha : μ > μ 0 ah Daer an H 0 ima r e n Pe Luas daerah terarsir = α Daerah penolakan H 0 0 t(db; α) Titik kritis z atau t

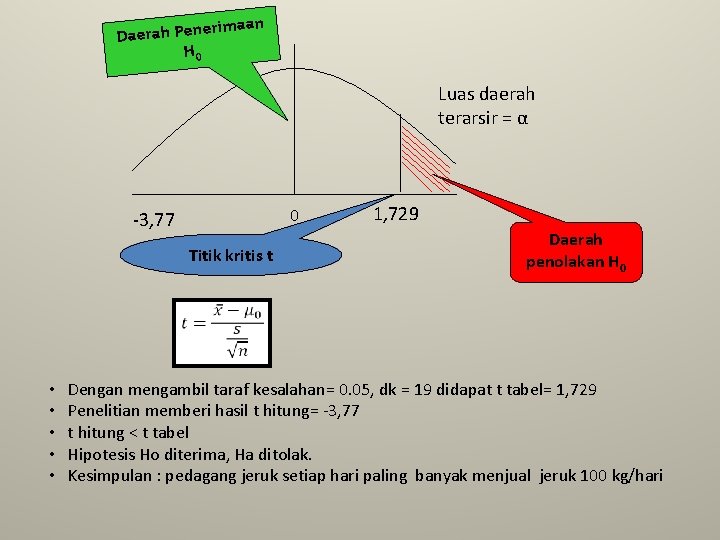
Contoh Uji Pihak Kanan : Terdapat suatu penelitian untuk mengetetahui berapa kg jeruk yang dapat terjual oleh pedagang setiap harinya. Berdasarkan pengamatan sepintas terhadap perdagangan jeruk, peneliti mengajukan hipotesis bahwa pedagang jeruk setiap hari paling banyak menjual 100 kg jeruk kepada konsumen. Dilakukan pengumpulan data terhadap 20 pedagang jeruk: 98, 80, 120, 90, 70, 100, 60, 85, 95, 100 70, 95, 90, 85, 75, 90, 70, 90, 60, 110 Penyelesaian : • Hip. Penelitian: . . . . • Hip. Statistik: . . . . • • N = 20 dk = 20 -1=19 S = 15, 83 µo = 100 X bar = 86. 65

rimaan Daerah Pene H 0 Luas daerah terarsir = α 0 -3, 77 Titik kritis t • • • 1, 729 Daerah penolakan H 0 Dengan mengambil taraf kesalahan= 0. 05, dk = 19 didapat t tabel= 1, 729 Penelitian memberi hasil t hitung= -3, 77 t hitung < t tabel Hipotesis Ho diterima, Ha ditolak. Kesimpulan : pedagang jeruk setiap hari paling banyak menjual jeruk 100 kg/hari

TUGAS Telah dilakukan pengumpulan data ttg produktifitas padi di kabupaten Cianjur. Berdasarkan sampel 20 lokasi penelitian diperoleh data ttg produktifitas padi tiap hektar dalam satuan ton sbb: 7 10 9 8 5 6 5 7 4 6 6 8 6 7 4 6 8 7 4 3 hipotesis penelitiannya ada 3: 1. produktifitas padi = 8 ton/ha 2. produktifitas padi paling sedikit 5 ton/ha 3. produktifitas padi paling tinggi 10 ton/ha Pertanyaannya: a. Tuliskan hipotesis penelitian dan statistiknya b. Gunakan uji t untuk menguji hipotesis itu c. Tuliskan kesimpulan dan gambarnya.

TERIMA KASIH