PENGOLAHAN CITRA DAN POLA PERTEMUAN 5 STIKI INDONESIA

PENGOLAHAN CITRA DAN POLA PERTEMUAN 5 STIKI INDONESIA 2012

Filter Spasial Linier p Bekerja dengan cara konvolusi p Filter Rata-Rata p Filter Gaussian Here comes your footer Page 2

Filter Gaussian p Untuk menentukan nilai-nilai setiap elemen dalam filter Gaussian yang akan dibentuk digunakan persamaan berikut : p Elemen-elemen filter Gaussian bisa ditentukan bila nilai σ2 dan ukuran filter N x N ditentukan terlebih dahulu dan nilai pada (0, 0) diseting sama dengan 1 Here comes your footer Page 3

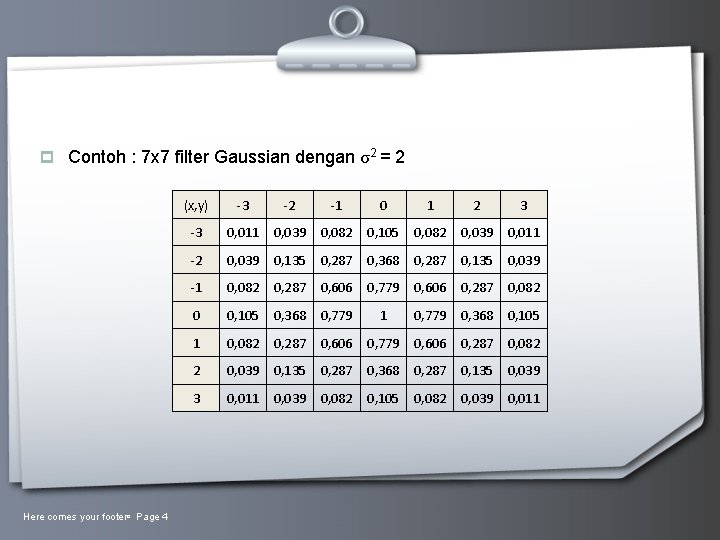
p Contoh : 7 x 7 filter Gaussian dengan σ2 = 2 Here comes your footer Page 4 (x, y) -3 -2 -1 0 1 2 3 -3 0, 011 0, 039 0, 082 0, 105 0, 082 0, 039 0, 011 -2 0, 039 0, 135 0, 287 0, 368 0, 287 0, 135 0, 039 -1 0, 082 0, 287 0, 606 0, 779 0, 606 0, 287 0, 082 0 0, 105 0, 368 0, 779 1 0, 779 0, 368 0, 105 1 0, 082 0, 287 0, 606 0, 779 0, 606 0, 287 0, 082 2 0, 039 0, 135 0, 287 0, 368 0, 287 0, 135 0, 039 3 0, 011 0, 039 0, 082 0, 105 0, 082 0, 039 0, 011

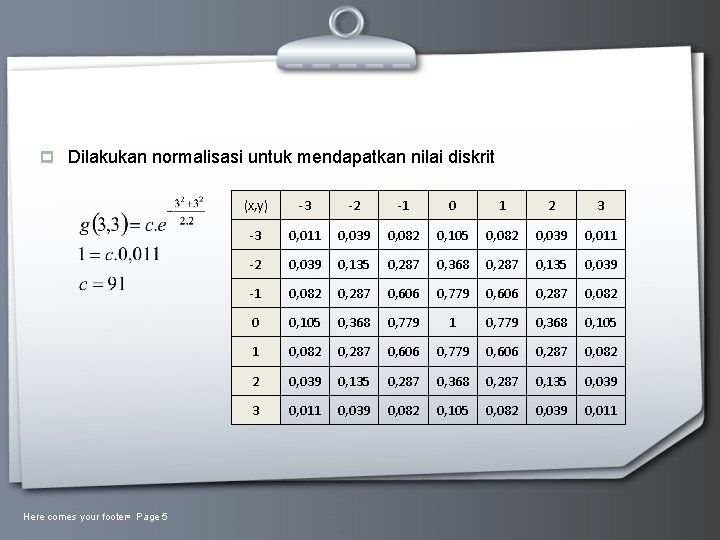
p Dilakukan normalisasi untuk mendapatkan nilai diskrit Here comes your footer Page 5 (x, y) -3 -2 -1 0 1 2 3 -3 0, 011 0, 039 0, 082 0, 105 0, 082 0, 039 0, 011 -2 0, 039 0, 135 0, 287 0, 368 0, 287 0, 135 0, 039 -1 0, 082 0, 287 0, 606 0, 779 0, 606 0, 287 0, 082 0 0, 105 0, 368 0, 779 1 0, 779 0, 368 0, 105 1 0, 082 0, 287 0, 606 0, 779 0, 606 0, 287 0, 082 2 0, 039 0, 135 0, 287 0, 368 0, 287 0, 135 0, 039 3 0, 011 0, 039 0, 082 0, 105 0, 082 0, 039 0, 011

p Hasil filter Gaussian Here comes your footer Page 6 1 4 7 10 7 4 12 26 33 26 12 4 7 26 55 71 55 26 7 10 33 71 91 71 33 10 7 26 55 71 55 26 7 4 12 26 33 26 12 4 1 33 7 10 7 33 1

Filter Spasial Non Linier p Disebut juga Order-statistic Filters p Didasarkan pada pengurutan dari intensitas pixel-pixel tetangga yang dilingkupi oleh filter-filter tersebut p Filter Maksimum p Filter Minimum p Filter Median Here comes your footer Page 7

Operasi Geometri p Memodifikasi koordinat piksel dalam suatu citra dengan pendekatan tertentu p Operasi Geometri, antara lain : ü Pencerminan (flipping) ü Rotasi/pemutaran (Rotating) ü Pemotongan (Cropping) ü Penskalaan (Scaling/Zooming)

Operasi Pencerminan (Flipping) • Efek pencerminan horisontal : pencerminan pada sumbu Y vertikal : pencerminan pada sumbu X kombinasi : pencerminan pada sumbu Y dan X

Operasi Pencerminan (Flipping) • Pencerminan Horizontal x’ = w – 1 – x y’ = y p Pencerminan Vertikal x’ = x y’ = h – 1 - y p Pencerminan Kombinasi x’ = w – 1 – x y’ = h – 1 - y

ROTASI (ROTATING) Ø Operasi rotasi dengan memutar koordinat yang akan dibahas adalah rotasi ¼ putaran (900) dan ½ putaran (1800). Ø Rotasi ¼ putaran (900) searah jarum jam (CW/clock wise) w’ = h dan h’ = w pertukaran ukuran lebar & tinggi citra x’ = w’ – 1 – y y’ = x Ø Rotasi ½ putaran (1800) searah jarum jam (CW/clock wise) x’ = w’ – 1 – x y’ = h’ – 1 – y

Rotasi (2) Rotasi Bebas Dengan asumsi berlawanan arah jarum jam (CCW/counter clock wise) x’ = x cos(θ) + y sin(θ) y’ = -x sin(θ) + y cos(θ) w’ = |w cos(θ)| + |h sin(θ)| h’ = |w sin(θ)| + |h cos(θ)|

½ putaran (250 CCW) (1800 CW) 1/4 putaran (900 CW)

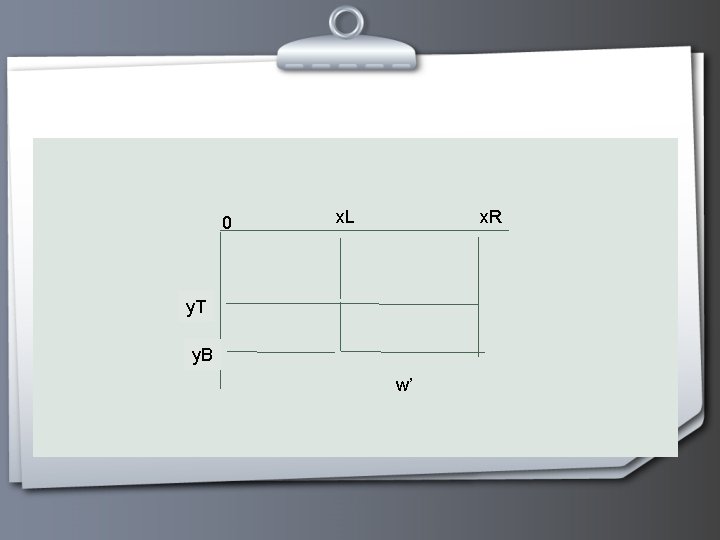
PEMOTONGAN (CROPPING) Adalah pengolahan citra dengan kegiatan memotong satu bagian dari citra. Rumus yang digunakan : x’ = x – x. L untuk x = x. L sampai x. R y’ = y – y. T untuk y = y. T sampai y. B (x. L, y. T) dan (x. R, y. B) adalah koordinat titik pojok kiri atas dan pojok kanan bawah citra yang akan di-crop Ukuran citra menjadi : w’ = x. R – x. L h’ = y. B –YT h’

0 x. L x. R y. T y. B w’

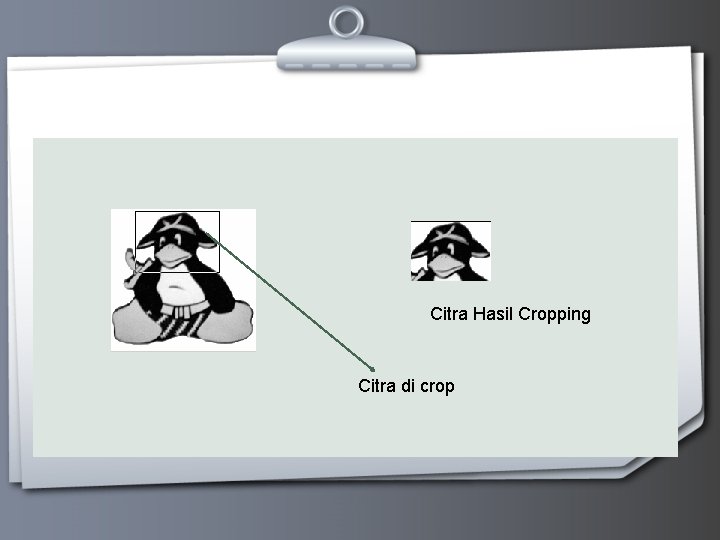
Citra Hasil Cropping Citra di crop

p Memperbesar (Zoom In) atau memperkecil (Zoom Out) citra p Nilai skala: p > 1, memperbesar skala p < 1, memperkecil skala p Scaling : x’ = Sh x w’ = Sh w y’ = Sv y h’ = Sv h Here comes your footer Page 18

Citra Asli Sh = 1 Sv = 2

Referensi p Gonzalez, Rafael C. and Woods, Richard E. . Digital Image Processing, 2 nd Ed. . 2002. New Jersey : Prentice Hall. p Putra, I Ketut Gede Darma. 2010. Pengolahan Citra Digital. Yogyakarta : Andi Offset. p Sutoyo, T. , dkk. 2009. Teori Pengolahan Citra Digital. Yogyakarta : Andi Offset. Here comes your footer Page 20