Penggunaan Statistik Dalam BIS Konsep Dasar Penggambaran Data

Penggunaan Statistik Dalam BIS Konsep Dasar Penggambaran Data Mengukur Hubungan Covariance dan Correlation Optimasi

Konsep Dasar Analisis Data, Informasi, dan Knowledge Populasi dan Sampel Variabel dan Observasi Tipe Data (Value): Categorical and Numerical (event): Cross Sectional dan Time Ordered (Series)

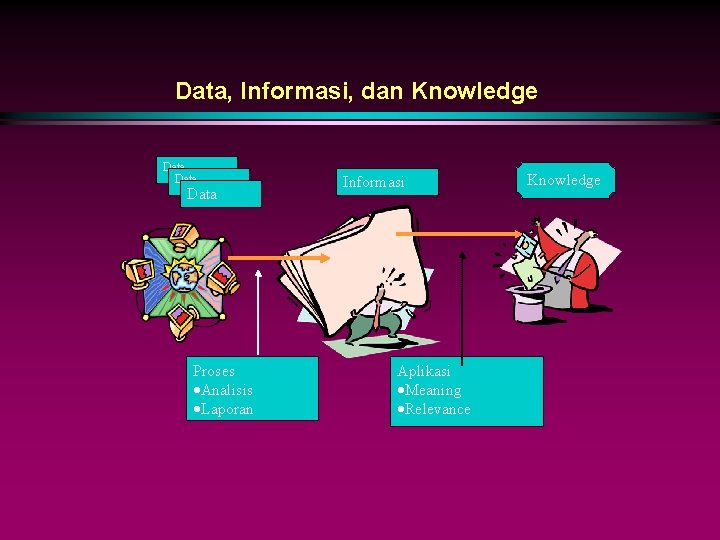
Data, Informasi, dan Knowledge Data Proses ·Analisis ·Laporan Informasi Aplikasi ·Meaning ·Relevance Knowledge

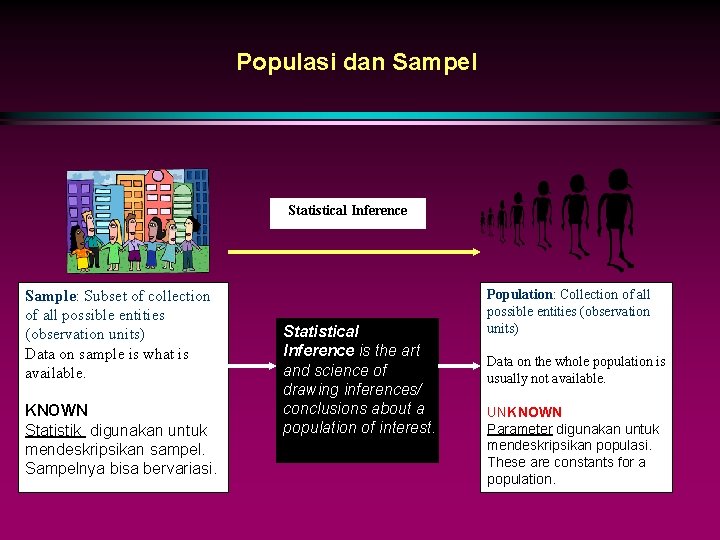
Populasi dan Sampel Statistical Inference Sample: Subset of collection of all possible entities (observation units) Data on sample is what is available. KNOWN Statistik digunakan untuk mendeskripsikan sampel. Sampelnya bisa bervariasi. Statistical Inference is the art and science of drawing inferences/ conclusions about a population of interest. Population: Collection of all possible entities (observation units) Data on the whole population is usually not available. UNKNOWN Parameter digunakan untuk mendeskripsikan populasi. These are constants for a population.

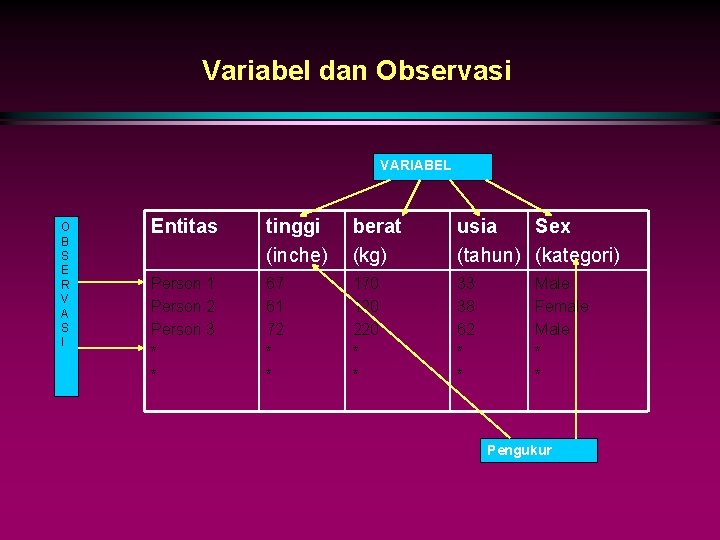
Variabel dan Observasi VARIABEL O B S E R V A S I Entitas tinggi berat (inche) (kg) usia Sex (tahun) (kategori) Person 1 Person 2 Person 3 * * 67 61 72 * * 33 38 62 * * 170 120 220 * * Male Female Male * * Pengukur

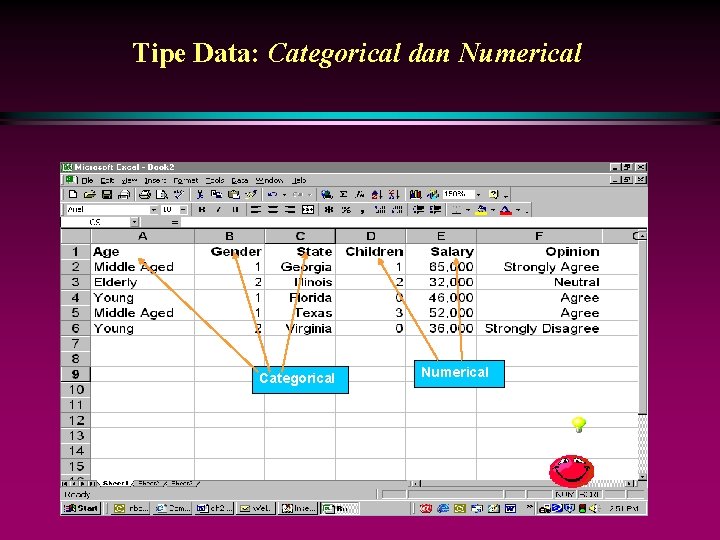
Tipe Data: Categorical dan Numerical Categorical Numerical

Cross-sectional and Time Ordered

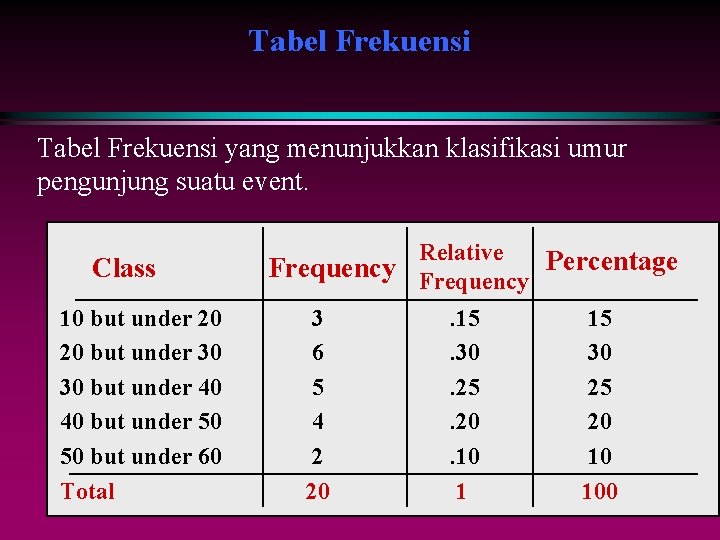
Tabel Frekuensi yang menunjukkan klasifikasi umur pengunjung suatu event. Class 10 but under 20 20 but under 30 30 but under 40 40 but under 50 50 but under 60 Total Relative Frequency Percentage 3 6 5 4 2 20 . 15. 30. 25. 20. 10 1 15 30 25 20 10 100

Histogram Distribusi Frekuensi

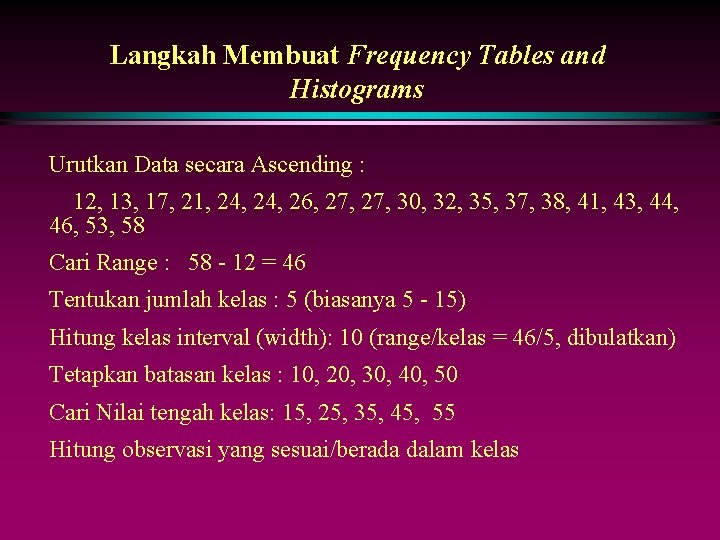
Langkah Membuat Frequency Tables and Histograms Urutkan Data secara Ascending : 12, 13, 17, 21, 24, 26, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58 Cari Range : 58 - 12 = 46 Tentukan jumlah kelas : 5 (biasanya 5 - 15) Hitung kelas interval (width): 10 (range/kelas = 46/5, dibulatkan) Tetapkan batasan kelas : 10, 20, 30, 40, 50 Cari Nilai tengah kelas: 15, 25, 35, 45, 55 Hitung observasi yang sesuai/berada dalam kelas

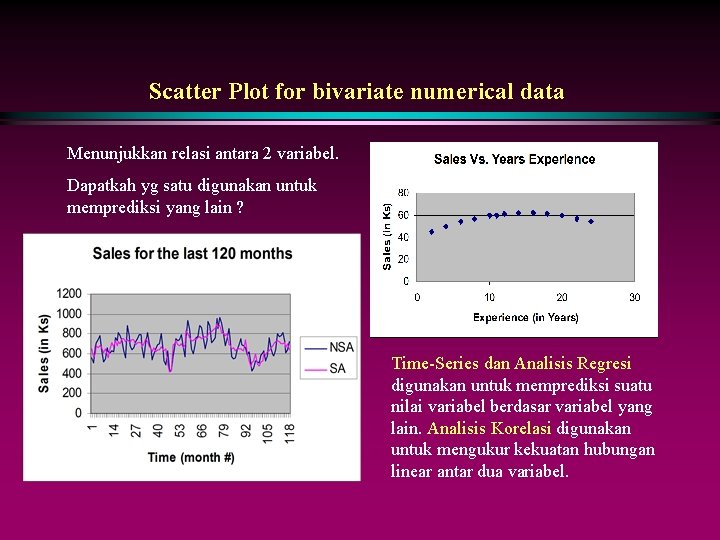
Scatter Plot for bivariate numerical data Menunjukkan relasi antara 2 variabel. Dapatkah yg satu digunakan untuk memprediksi yang lain ? Time-Series dan Analisis Regresi digunakan untuk memprediksi suatu nilai variabel berdasar variabel yang lain. Analisis Korelasi digunakan untuk mengukur kekuatan hubungan linear antar dua variabel.

Penggambaran Data: Summary Measures Mengukur Central Tendency (CT) Mean, Median, Mode Mengukur Variasi Range, Varian dan Standar Deviasi

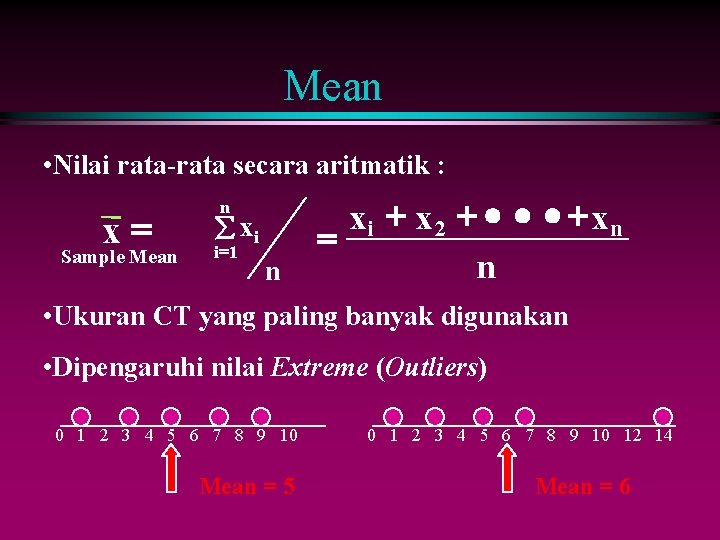
Mean • Nilai rata-rata secara aritmatik : x= Sample Mean n å xi i =1 n xi + x 2 + · · · + xn = n • Ukuran CT yang paling banyak digunakan • Dipengaruhi nilai Extreme (Outliers) 0 1 2 3 4 5 6 7 8 9 10 Mean = 5 0 1 2 3 4 5 6 7 8 9 10 12 14 Mean = 6

Median • Ukuran penting dari Central Tendency • Nilai tengah dari n data yang diurutkan, • If n is odd, the median is the middle number. • If n is even, the median is the average of the 2 middle numbers. • Tidak dipengaruhi Extreme Values 0 1 2 3 4 5 6 7 8 9 10 Median = 5 0 1 2 3 4 5 6 7 8 9 10 12 14 Median = 5

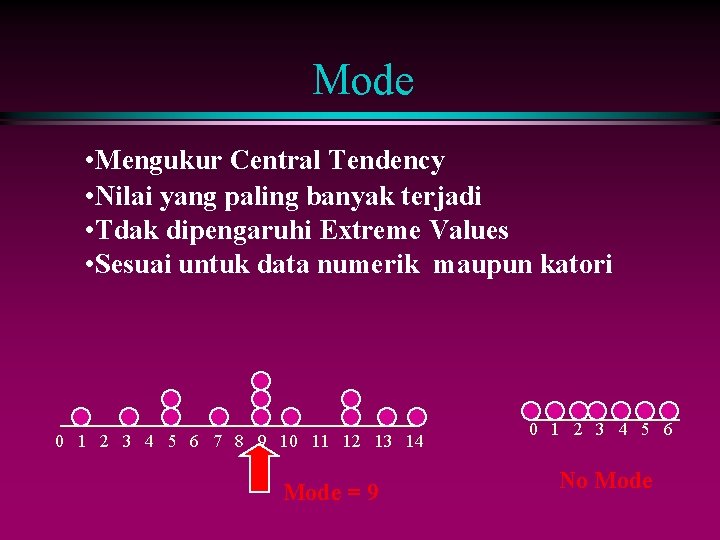
Mode • Mengukur Central Tendency • Nilai yang paling banyak terjadi • Tdak dipengaruhi Extreme Values • Sesuai untuk data numerik maupun katori 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Mode = 9 0 1 2 3 4 5 6 No Mode

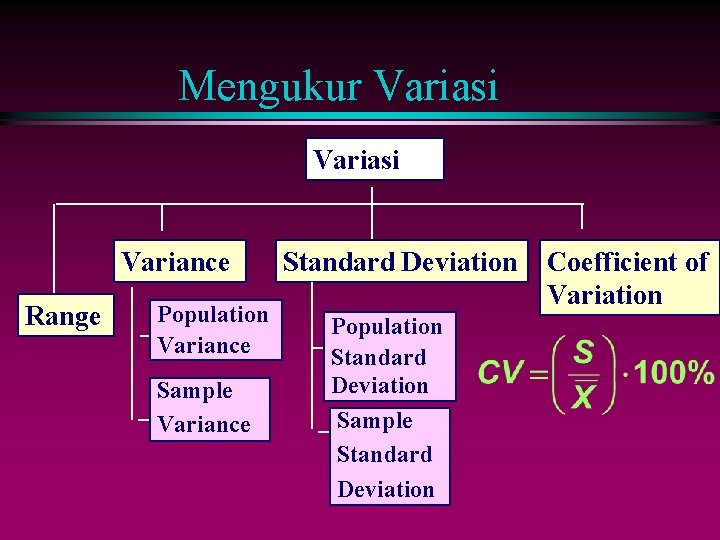
Mengukur Variasi Variance Range Population Variance Sample Variance Standard Deviation Population Standard Deviation Sample Standard Deviation Coefficient of Variation

Range • Menentukan Variasi • Beda antara observasi paling besar & paling kecil : Range = x Largest - x Smallest • Abaikan bagaimana sebaran datanya : Range = 12 - 7 = 5 7 8 9 10 11 12

Variance • Pentingnya menentikan Variasi • Shows Variation About the Mean: 2 ) m 2 å (Xi • Untuk Populasi : s = N • Untuk Sample: Untuk Populasi : gunakan N dalam denominator. ( -X) å X i s = n -1 2 2 Untuk Sample : gunakan n - 1 dalam denominator.

Standard Deviasi • Paling penting menentukan Variasi • Tunjukkan Variasi tentang Mean: 2 ( ) m å Xi • Untuk Populasi: s= N • Untuk Sample: Untuk Populasi: gunakan N dalam denominator. s = å (X i - X n -1 ) 2 Untuk Sample : gunakan n - 1 dalam denominator.

Sample Standard Deviation ( - X) å X i s = n-1 Data: 10 2 12 n=8 For the Sample : use n - 1 in the denominator. 14 15 17 18 18 Mean =16 s= Sample Standard Deviation= 4. 2426 24

Comparing Standard Deviations Data A 11 12 13 14 15 16 17 18 19 20 21 Data B 11 12 13 14 15 16 17 18 19 20 21 Data C 11 12 13 14 15 16 17 18 19 20 21 Mean = 15. 5 s = 3. 338 Mean = 15. 5 s =. 9258 Mean = 15. 5 s = 4. 57

Coefficient of Variation l. Measure of Relative Variation l. Always a% l. Shows Variation Relative to Mean l. Used to Compare 2 or More Groups l. Formula ( for Sample):

Comparing Coefficient of Variation Stock A: Average Price last year = $50 l Standard Deviation = $5 l Stock B: Average Price last year = $100 l Standard Deviation = $5 l Coefficient of Variation: Stock A: CV = 10% Stock B: CV = 5%

Shape Menggambarkan bagaimana data berdistribusi Mengukur kelancipan : Symmetric or skewed Left-Skewed Mean Median Mode Symmetric Mean = Median = Mode Right-Skewed Mode Median Mean

Mengukur Hubungan - Regresi

Least Squares Estimation l l l Untuk mengetahui hubungan linier antara 2 variabel dapat dilakukan dengan menggambarkan garis lurus yang mendekati titik-titik pasangan nilai ke dua variabel tersebut. Membutuhkan proses secara sistematis dan tidak hanya garis random. Harus dipilih garis dimana jarak vertikal antara garis dan titik (residual) seminimal mungkin. Perlu dipilih garis yang memenuhi smallest sum of the squared residuals. Garis tersebut disebut least squares line.

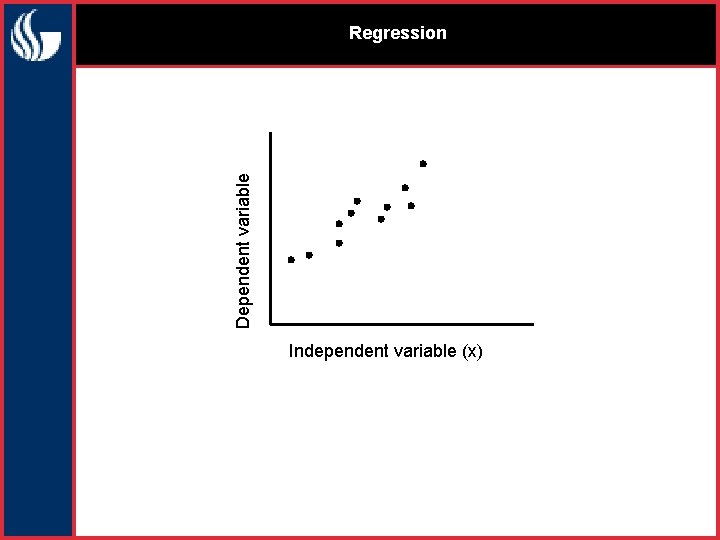
Dependent variable Regression Independent variable (x)

Dependent variable (y) Simple Linear Regression є y’ = b 0 + b 1 X ± є b 0 (y intercept) Independent variable (x) B 1 = slope = ∆y/ ∆x

Simple Linear Regression Prediction error: ε Observation: y ^ Prediction: y Zero For each observation, the variation can be described as: y=^ y+ε Actual = Explained + Error

• Garis terbaik adalah garis dimana jumlah kuadrat dari residu ε adalah minimal

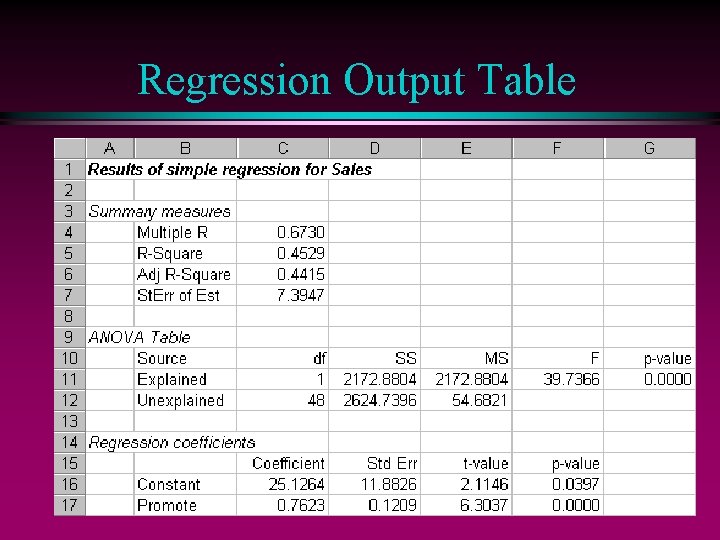
Regression Output Table

The Regression Output l Persamaan Regresi Predicated Sales = 25. 1264 + 0. 7623 Promote Interpretasi : n Koefisien / slope 0. 7623 menunjukkan bahwa index Sales akan cenderung meningkat sebesar 0, 76 untuk setiap penambahan satu unit index pengeluaran promosi. n Intercept tidak terlalu penting dalam analisis, nilai tersebut menunjukkan pengaruh diluar variabel promosi.

Multiple Regression Predicted Overhead = 3997 + 43. 45 Mach. Hrs + 883. 62 Prod. Runs

Interpretasi Persamaan l l Interpretasi dari persamaan tersebut adalah pada sejumlah produksi konstan maka overhead cost diperkirakan bertambah sebesar $43. 54 untuk setiap penambahan 1 jam extra machine; dan jika machine hours tetap, overhead diperkirakan meningkat $883. 62 untuk setiap extra production run. Manajer dapat menintepretasikan $3997 sebagai componen tetap overhead diluar Mach. Hrs and Prod. Runs.

MODEL OPTIMASI EXTERNAL INPUTS OUTPUT MODEL DECISION INPUTS Model optimasi menjawab pertanyaan, “Nilai keputusan apa yang memberikan output terbaik? ”

SCARCITY CONSTRAINTS DECISION INPUTS Optimasi muncul karena sumber daya yang terbatas.

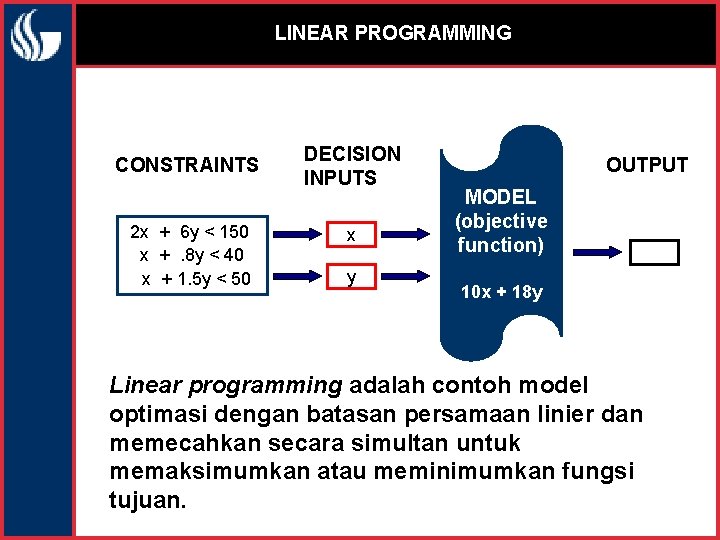
LINEAR PROGRAMMING CONSTRAINTS 2 x + 6 y < 150 x + . 8 y < 40 x + 1. 5 y < 50 DECISION INPUTS x y OUTPUT MODEL (objective function) 10 x + 18 y Linear programming adalah contoh model optimasi dengan batasan persamaan linier dan memecahkan secara simultan untuk memaksimumkan atau meminimumkan fungsi tujuan.

EXAMPLE 1: BOB’S MUFFLER SHOP Bob memproduksi 2 jenis muffler, keluarga dan olahraga. Setiap muffler keluarga memberi keuntungan $ 10 dan setiap muffler olahraga $ 18. Angka-angka ini dikenal sebagai 'margin kontribusi' produk '. Keuntungannya ditentukan oleh 18 s fungsi $ 10 f + $, di mana f dan s adalah jumlah total dari setiap jenis knalpot dijual. Ini adalah fungsi tujuannya. Variabel keputusannya adalah berapa jumlah muffler keluarga dan olahraga untuk diproduksi setiap bulan. Dalam situasi tak terbatas, ia ingin menjual muffler olahraga sebanyaknya karena kontribusi mereka lebih tinggi. Namun. . .

EXAMPLE 1: BACKGROUND Dalam rangka untuk menciptakan sebuah knalpot, Bob harus menggunakan braket, tukang, dan aluminium. Sumber daya yang dibutuhkan untuk masing-masing jenis: Family Sports Brackets 2. 00 6. 00 Labor hours 1. 00 0. 80 1 1. 5 Max Alloy Dalam hitungan bulan ia mengalam keterbatasan dalam sumber daya: Ini masalah konstrain. Quantity Brackets 150 Labor hours 40 Max Alloy 50

EXAMPLE 1: Memodelkan konstrain sebagai Persamaan Linear Konstrain dapat dimodelkan sebagai persamaan linear: 2 f + 6 s ≤ 150 f +. 8 s ≤ 40 50 f + 33. 33 s ≤ 50 (brackets) (labor) (alloy) Bob juga memiliki kontrak yang luar biasa yang memaksa dia untuk memproduksi 5 muffler bergaya sport setiap bulan dan tahu, dari historis kinerja, bahwa permintaan muffler keluarga pada bulan tertentu tidak akan melebihi 35. Kendala ini dapat dimodelkan sebagai: f ≤ 35 s ≥ 5 (maximum demand) (contractual obligation) Fungsi obyektif (profit) adalah : 10 f + 18 s

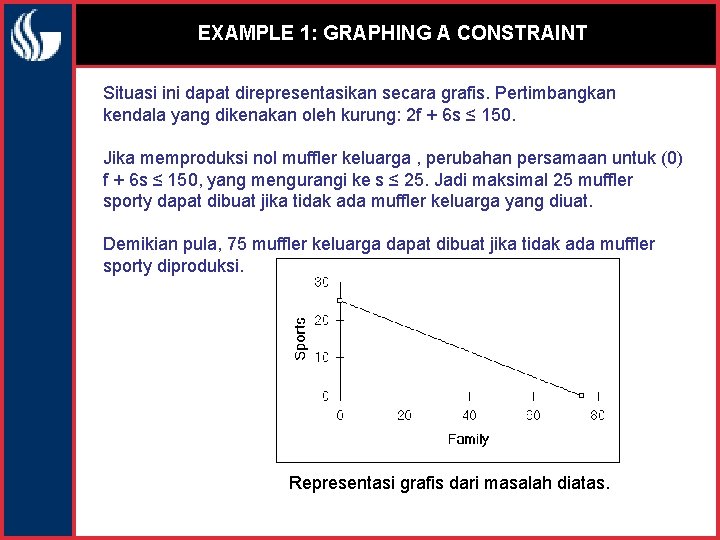
EXAMPLE 1: GRAPHING A CONSTRAINT Situasi ini dapat direpresentasikan secara grafis. Pertimbangkan kendala yang dikenakan oleh kurung: 2 f + 6 s ≤ 150. Jika memproduksi nol muffler keluarga , perubahan persamaan untuk (0) f + 6 s ≤ 150, yang mengurangi ke s ≤ 25. Jadi maksimal 25 muffler sporty dapat dibuat jika tidak ada muffler keluarga yang diuat. Demikian pula, 75 muffler keluarga dapat dibuat jika tidak ada muffler sporty diproduksi. Representasi grafis dari masalah diatas.

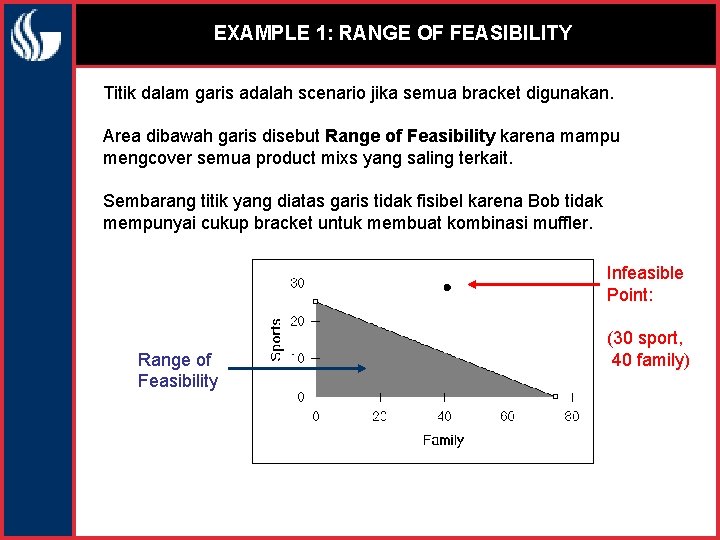
EXAMPLE 1: RANGE OF FEASIBILITY Titik dalam garis adalah scenario jika semua bracket digunakan. Area dibawah garis disebut Range of Feasibility karena mampu mengcover semua product mixs yang saling terkait. Sembarang titik yang diatas garis tidak fisibel karena Bob tidak mempunyai cukup bracket untuk membuat kombinasi muffler. Infeasible Point: Range of Feasibility (30 sport, 40 family)

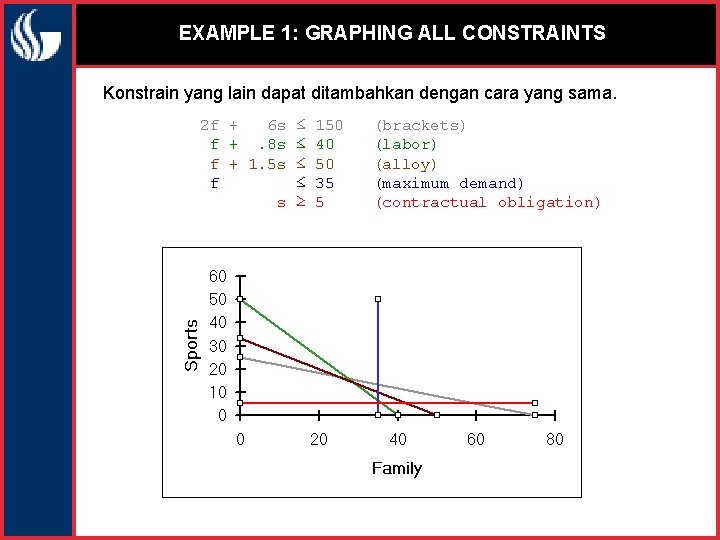
EXAMPLE 1: GRAPHING ALL CONSTRAINTS Konstrain yang lain dapat ditambahkan dengan cara yang sama. 2 f + 6 s ≤ f +. 8 s ≤ f + 1. 5 s ≤ f ≤ s ≥ 150 40 50 35 5 (brackets) (labor) (alloy) (maximum demand) (contractual obligation)

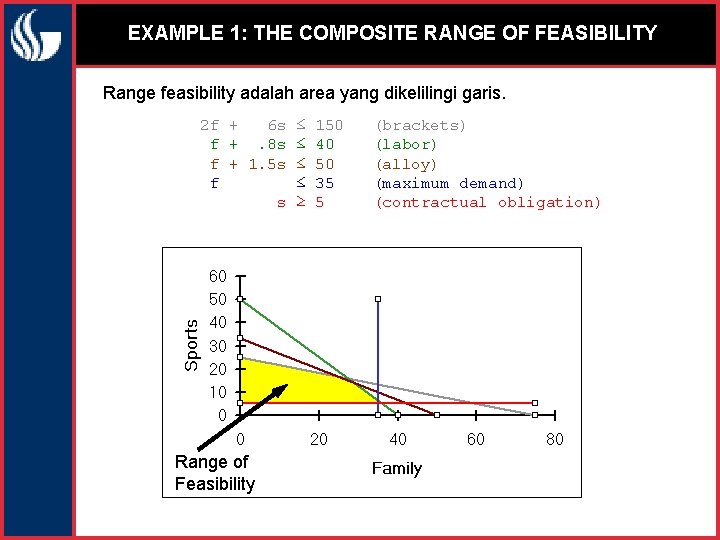
EXAMPLE 1: THE COMPOSITE RANGE OF FEASIBILITY Range feasibility adalah area yang dikelilingi garis. 2 f + 6 s ≤ f +. 8 s ≤ f + 1. 5 s ≤ f ≤ s ≥ Range of Feasibility 150 40 50 35 5 (brackets) (labor) (alloy) (maximum demand) (contractual obligation)

EXAMPLE 1: POTENTIAL PROFIT LINES Fungsi laba akan membentuk garis dengan kemiringan -5 / 9, rasio kontribusi margin muffler keluarga untuk muffler olahraga. Setiap baris berhubungan dengan tingkat tertentu dari total keuntungan. Semakin jauh keluar garis, semakin besar jumlah laba. Total Profit: $100 $190 $280 $370 $460 $550

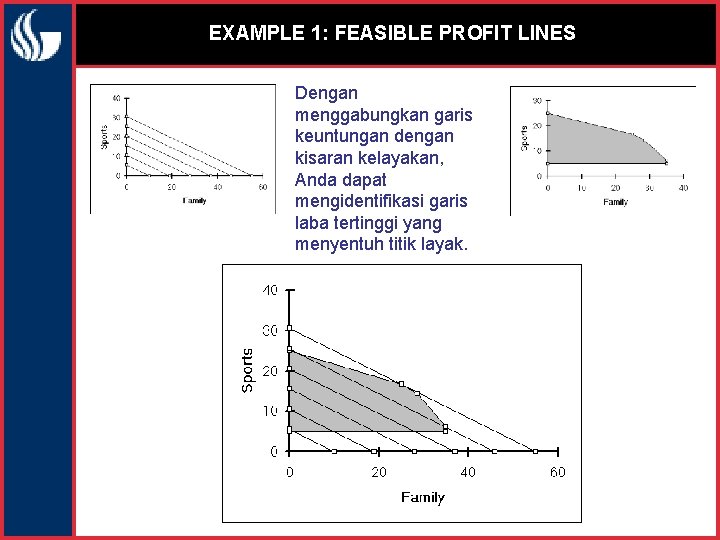
EXAMPLE 1: FEASIBLE PROFIT LINES Dengan menggabungkan garis keuntungan dengan kisaran kelayakan, Anda dapat mengidentifikasi garis laba tertinggi yang menyentuh titik layak.

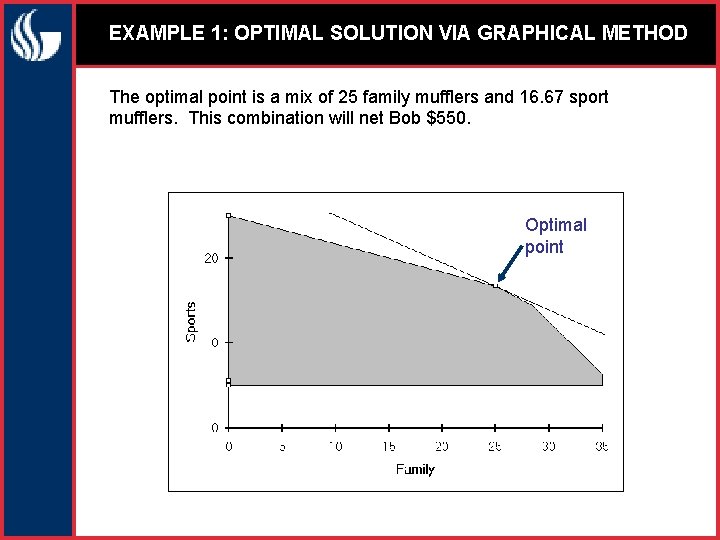
EXAMPLE 1: OPTIMAL SOLUTION VIA GRAPHICAL METHOD The optimal point is a mix of 25 family mufflers and 16. 67 sport mufflers. This combination will net Bob $550. Optimal point