PENGERTIAN Metode Secant baca sekan merupakan modifikasi metode

PENGERTIAN Metode Secant (baca: “sekan”) merupakan modifikasi metode Newton-Raphson. Pada metode Newton-Raphson, pada setiap proses iterasinya memerlukan perhitungan nilai dua buah fungsi, yakni f(xn) dan f’(xn). Apabila kedua fungsi tersebut tidak rumit, metode tersebut mungkin sangat baik mengingat kekonvergenannya. Akan tetapi, tidak semua fungsi dapat diturunkan dengan mudah, terutama fungsi-fungsi yang rumit.

Sedangkan metode Secant hanya memerlukan satu fungsi saja yaitu f(xn), yang jika pemrogramannya dilakukan dengan benar, maka nilainya dapat diperoleh dari iterasi sebelumnya f(xn-1). Sehingga metode Secant akan memerlukan waktu yang lebih sedikit untuk tiap iterasinya dari pada metode Newton.

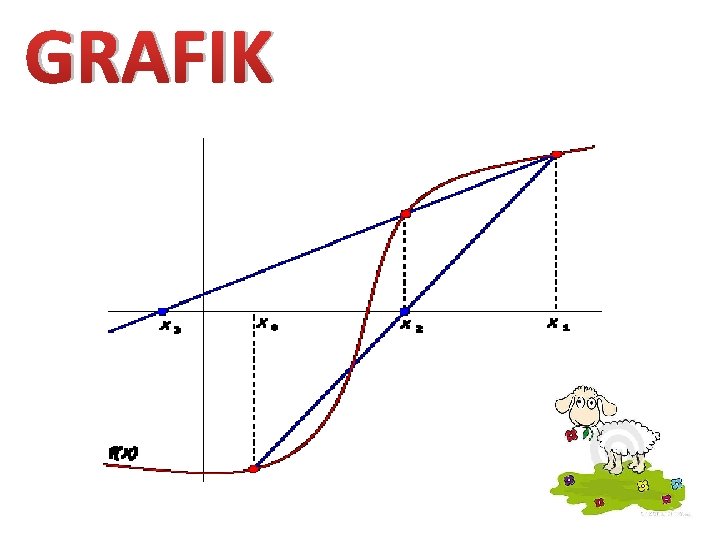
GRAFIK

Kelebihan • Tidak memerlukan perhitungan turunan • Secara lokal, laju kekonvergenannya superlinier jika sudah dekat ke akar yang dicari. • Galat hampiran dapat diestimasi • Lebih mudah diimplementasikan daripada metode Newton. • Dua langkah iterasi metode TB hampir setara dengan satu langkah iterasi Newton.

Kekurangan • Memerlukan dua hampiran awal • Kekonvergenan tidak dijamin untuk iterasi yang jauh dari akar yang dicari. • Kekonvergenannya mungkin lambat atau tidak sama sekali. • Laju kekonvergenannya tidak secepat metode Newton. • Kriteria penghentian iterasi tidak jelas.

CONTOH PROGRAM clc; clear; disp('Program Metode Secant'); disp('****************'); x 0=input('Masukkan X 0 : '); xb=input('Masukkan X 1 : '); a=0; e=10; disp('------------------------------------------'); disp(' a X 0 X 1 f(X 0) f(X 1) x 2 e'); disp('------------------------------------------'); while e>0. 0001 fx=x 0^2 -4; fxb=xb^2 -4; d = xb - (fxb*(xb-x 0)/(fxb-fx)); e=abs(x 0 -xb); x 0 = xb; xb = d; a=a+1; fprintf('%3. 0 f %12. 6 fn', a, x 0, xb, fxb, d, e) end; disp('________________________________'); fprintf('Akarnya Adalah = %10. 8 fn', xb);

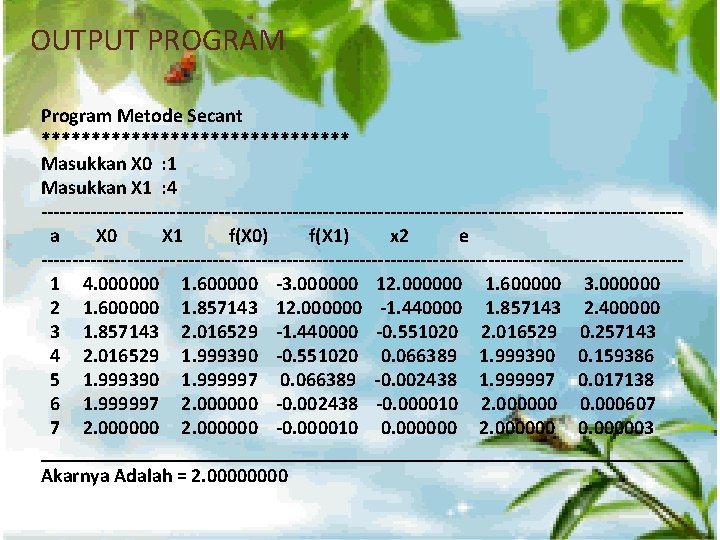
OUTPUT PROGRAM Program Metode Secant **************** Masukkan X 0 : 1 Masukkan X 1 : 4 ----------------------------------------------------a X 0 X 1 f(X 0) f(X 1) x 2 e ----------------------------------------------------1 4. 000000 1. 600000 -3. 000000 12. 000000 1. 600000 3. 000000 2 1. 600000 1. 857143 12. 000000 -1. 440000 1. 857143 2. 400000 3 1. 857143 2. 016529 -1. 440000 -0. 551020 2. 016529 0. 257143 4 2. 016529 1. 999390 -0. 551020 0. 066389 1. 999390 0. 159386 5 1. 999390 1. 999997 0. 066389 -0. 002438 1. 999997 0. 017138 6 1. 999997 2. 000000 -0. 002438 -0. 000010 2. 000000 0. 000607 7 2. 000000 -0. 000010 0. 000000 2. 000000 0. 000003 _________________________________ Akarnya Adalah = 2. 0000

clc; clear; disp('Program Metode Secant'); disp('****************'); x 0=input('Masukkan X 0 : '); xb=input('Masukkan X 1 : '); a=0; e=10; disp('------------------------------------------'); disp(' a X 0 X 1 f(X 0) f(X 1) x 2 e'); disp('------------------------------------------'); while e>0. 0001 fx=x 0^2 -3; fxb=xb^2 -3; d = xb - (fxb*(xb-x 0)/(fxb-fx)); e=abs(x 0 -xb); x 0 = xb; xb = d; a=a+1; fprintf('%3. 0 f %12. 6 fn', a, x 0, xb, fxb, d, e) end; disp('__________________________________________'); fprintf('Akarnya Adalah = %10. 8 fn', xb);

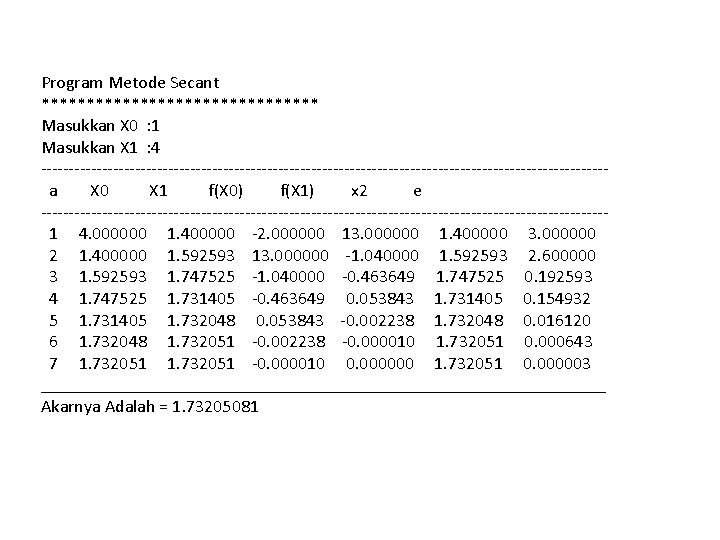
Program Metode Secant **************** Masukkan X 0 : 1 Masukkan X 1 : 4 ---------------------------------------------------a X 0 X 1 f(X 0) f(X 1) x 2 e ---------------------------------------------------1 4. 000000 1. 400000 -2. 000000 13. 000000 1. 400000 3. 000000 2 1. 400000 1. 592593 13. 000000 -1. 040000 1. 592593 2. 600000 3 1. 592593 1. 747525 -1. 040000 -0. 463649 1. 747525 0. 192593 4 1. 747525 1. 731405 -0. 463649 0. 053843 1. 731405 0. 154932 5 1. 731405 1. 732048 0. 053843 -0. 002238 1. 732048 0. 016120 6 1. 732048 1. 732051 -0. 002238 -0. 000010 1. 732051 0. 000643 7 1. 732051 -0. 000010 0. 000000 1. 732051 0. 000003 ________________________________ Akarnya Adalah = 1. 73205081