Pendimensian dan Evaluasi Kinerja Jaringan Telekomunikasi Rekayasa Trafik




![Tujuan optimasi (2) 4 Untuk pasangan [1, 2] : – A 1. 2 diambil Tujuan optimasi (2) 4 Untuk pasangan [1, 2] : – A 1. 2 diambil](https://slidetodoc.com/presentation_image_h/1d6a6fd3afa05fda78f6209582dbbddb/image-9.jpg)





















![SCR (3) 4 Jadi SCR = ASR x [1 -Lo-Le] – SCR Lokal ME SCR (3) 4 Jadi SCR = ASR x [1 -Lo-Le] – SCR Lokal ME](https://slidetodoc.com/presentation_image_h/1d6a6fd3afa05fda78f6209582dbbddb/image-38.jpg)

- Slides: 39

Pendimensian dan Evaluasi Kinerja Jaringan Telekomunikasi Rekayasa Trafik Sukiswo sukiswok@yahoo. com sukiswo@elektro. ft. undip. ac. id Rekayasa Trafik, Sukiswo 1

Outline 4 Pendimensian dan optimasi jaringan 4 Evaluasi NNGOS dengan metoda Gaudreau 4 Parameter kinerja Rekayasa Trafik, Sukiswo 2

Pendimensian dan Optimasi Jaringan 4 Data yang diperlukan – Matriks trafik – Matriks biaya – Ruting dan struktur jaringan – Kinerja jaringan yang diinginkan 4 Untuk menjamin keadilan optimasi 4 Our subject : optimasi menurut Pratt Rekayasa Trafik, Sukiswo 3

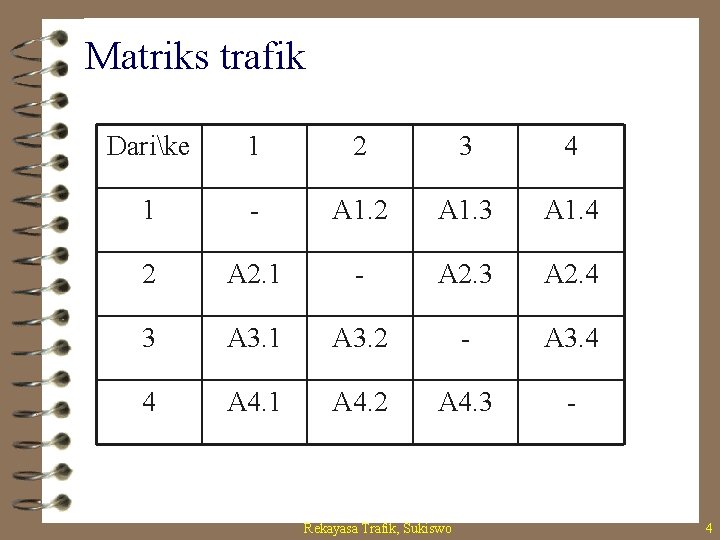
Matriks trafik Darike 1 2 3 4 1 - A 1. 2 A 1. 3 A 1. 4 2 A 2. 1 - A 2. 3 A 2. 4 3 A 3. 1 A 3. 2 - A 3. 4 4 A 4. 1 A 4. 2 A 4. 3 - Rekayasa Trafik, Sukiswo 4

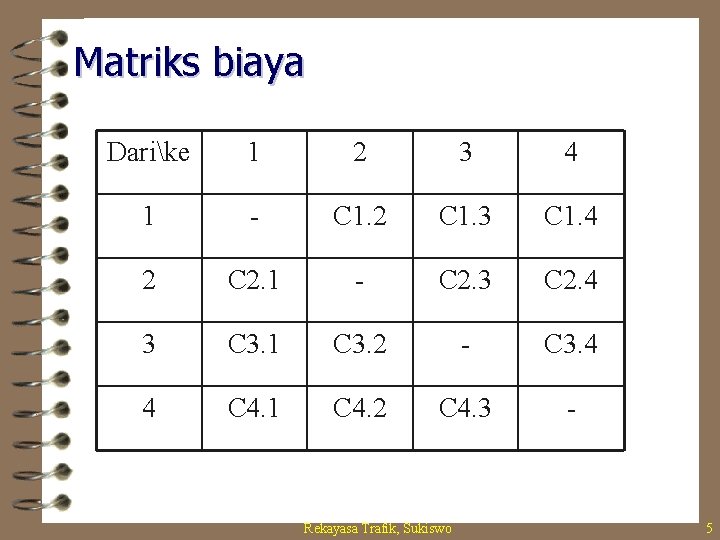
Matriks biaya Darike 1 2 3 4 1 - C 1. 2 C 1. 3 C 1. 4 2 C 2. 1 - C 2. 3 C 2. 4 3 C 3. 1 C 3. 2 - C 3. 4 4 C 4. 1 C 4. 2 C 4. 3 - Rekayasa Trafik, Sukiswo 5

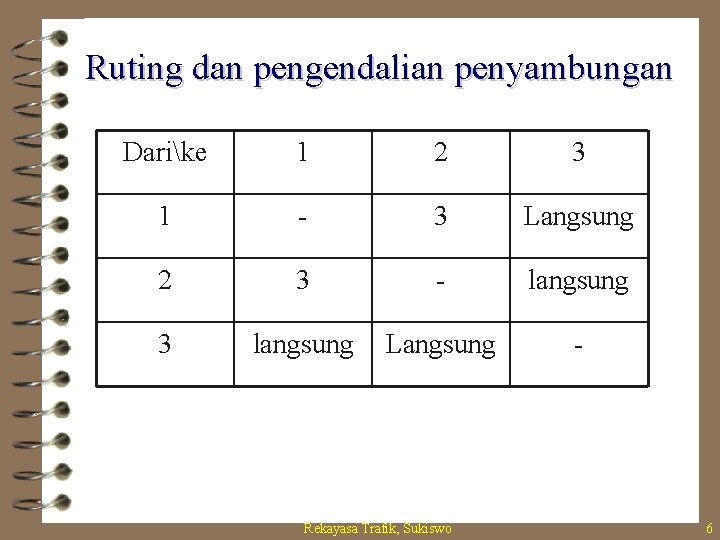
Ruting dan pengendalian penyambungan Darike 1 2 3 1 - 3 Langsung 2 3 - langsung 3 langsung Langsung - Rekayasa Trafik, Sukiswo 6

Kinerja jaringan yang diinginkan 4 Untuk data : tidak toleran terhadap error (harus error free/tidak diinginkan ada blocking/degradasi) dan tidak sensitif terhadap delay 4 Untuk telepon : toleran terhadap error (masih memungkinkan terjadinya blocking dengan tingkatan tertentu) tetapi sensitif terhadap delay – Kinerja jaringan yang diinginkan • Blocking di final route • NNGOS (end-to-end GOS) = end-to-end blocking • Yang biasa dipakai : Blocking di final route Rekayasa Trafik, Sukiswo 7

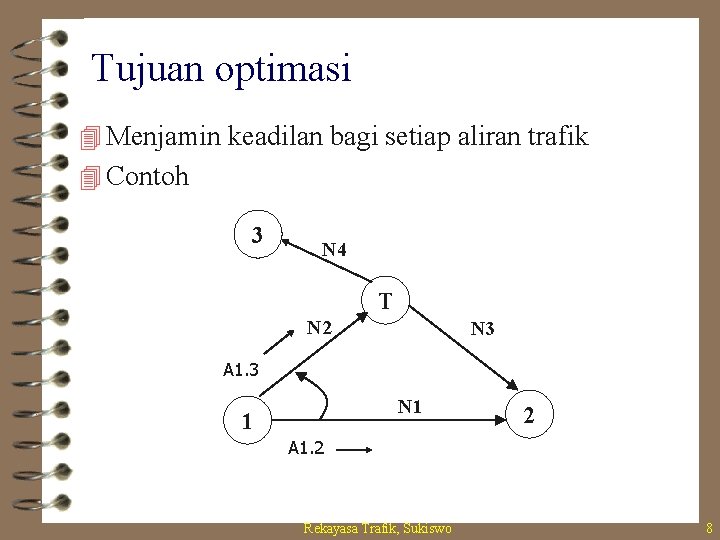
Tujuan optimasi 4 Menjamin keadilan bagi setiap aliran trafik 4 Contoh 3 N 4 T N 2 N 3 A 1. 3 N 1 1 2 A 1. 2 Rekayasa Trafik, Sukiswo 8
![Tujuan optimasi 2 4 Untuk pasangan 1 2 A 1 2 diambil Tujuan optimasi (2) 4 Untuk pasangan [1, 2] : – A 1. 2 diambil](https://slidetodoc.com/presentation_image_h/1d6a6fd3afa05fda78f6209582dbbddb/image-9.jpg)
Tujuan optimasi (2) 4 Untuk pasangan [1, 2] : – A 1. 2 diambil dari matriks trafik dan misalnya N 1 diketahui, maka trafik luap a (dengan m 1 dan v 1) dapat dihitung – Berkas N 2 merupakan berkas akhir (final route), jadi trafik yang tak dapat dimuat disini akan hilang – Trafik yang ditawarkan ke berkas N 2 • A 1. 3 (dengan M 1. 3 dan V 1. 3) dimana M 1. 3=V 1. 3 (Poisson) • a memiliki harga m 1 yang tidak sama dengan v 1 (non -Poisson dimana v 1 > m 1) Rekayasa Trafik, Sukiswo 9

Tujuan optimasi (3) • Sekarang harus didimensikan N 2 dengan B di N 2 = 1% – Ini berarti bahwa R 2=trafik yang hilang di N 2=1%(M 1. 3+m 1) – Jelas bahwa trafik hilang untuk A 1. 2 lebih kecil daripada 1% – Misalnya m 1=30%x. A 1. 2, maka trafik hilang untuk A 1. 2 di N 2 adalah kira-kira= 1%x 30%x. A 1. 2=0, 3%A 1. 2 – Jadi untung buat trafik A 1. 2 (tidak adil bagi A 1. 3) • Dengan fakta tersebut, maka diperlukan optimasi Rekayasa Trafik, Sukiswo 10

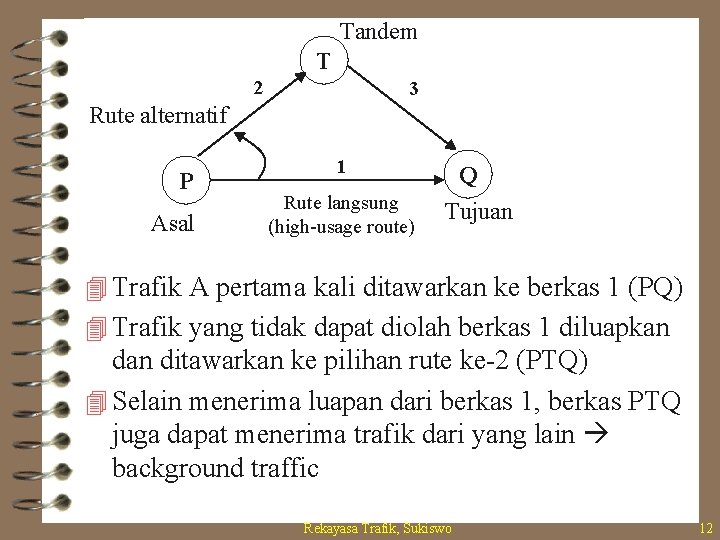
Optimasi menurut Pratt • Jaringan dasar Tandem T 2 3 Rute alternatif P Asal 1 Rute langsung (high-usage route) Q Tujuan • Yang menjadi acuan : biaya saluran • A = trafik yang ditawarkan ke high-usage route • N 1, N 2, N 3 = jumlah saluran yang diperlukan di berkas saluran 1, 2, dan 3 • C 1, C 2, C 3 = biaya per saluran di berkas saluran 1, 2, dan 3 Rekayasa Trafik, Sukiswo 11

Tandem T 2 3 Rute alternatif P Asal 1 Rute langsung (high-usage route) Q Tujuan 4 Trafik A pertama kali ditawarkan ke berkas 1 (PQ) 4 Trafik yang tidak dapat diolah berkas 1 diluapkan ditawarkan ke pilihan rute ke-2 (PTQ) 4 Selain menerima luapan dari berkas 1, berkas PTQ juga dapat menerima trafik dari yang lain background traffic Rekayasa Trafik, Sukiswo 12

4 Biaya untuk ruting trafik A dari P ke Q = C 4 C = C 1. N 1 + C 2. N 2 + C 3. N 3 4 Bila N 1 diketahui, maka N 2 dan N 3 bisa dihitung dengan syarat C 1, C 2, dan C 3 serta B di berkas final route (berkas 2 dan 3) diketahui 4 Untuk memperoleh C yang minimum, C diturunkan terhadap N 1 4 Penurunan N 2 dan N 3 terhadap N 1 dapat ditulis Rekayasa Trafik, Sukiswo 13

4 Agar diperoleh biaya yang minimum, maka Rekayasa Trafik, Sukiswo 14

disebut Marginal Occupancy (H), yaitu pertambahan 4 trafik yang dimuat pertambahan saluran bila trafik yang ditawarkan tetap, 4 H= , dimana m = trafik luap rata-rata disebut Marginal Capacity (b), yaitu pertambahan trafik 4 yang ditawarkan pertambahan saluran bila GOS (=B) tetap Rekayasa Trafik, Sukiswo 15

Perhitungan jumlah saluran dilakukan secara iterasi 1. Ambil harga b 2 dan b 3 kira-kira antara 0, 5 s. d. 0, 8. Biasanya ambil harga b = 0, 8 2. Hitung harga H 1 menggunakan harga biaya saluran yang diketahui 3. Cari harga N 1 yang memenuhi harga H 1 tersebut. (Lihat slide ) 4. Hitung harga trafik luap m 1 dan setelah digabungkan dengan background traffic, hitung N 2 dan N 3 dengan GOS (B 2=B 3=B) yang diketahui 5. Cari harga b 2 dan b 3 dengan N 2 dan N 3 yang sudah dicari Bila berbeda ulangi dari langkah 1, sampai tidak ada perbedaan (sedikit beda); Cara menghitung b dapat dilihat pada slide no 9 Rekayasa Trafik, Sukiswo 16

Menghitung harga H 4 Karena harga N bersifat diskrit, maka kita dapat menghitung harga H dengan cara berikut – H 1=[ Y/ N 1]A – Y=Y(N+1)-Y(N) • Y(N+1)=A[1 -BN+1(A)] • Y(N)= A[1 -BN(A)] – N 1=(N 1+1)-N 1=1 – Maka H 1=A[BN(A)-BN+1(A)] • H 1=ABN(A)-ABN+1(A) • Untuk mencari N dari harga H – carilah pada tabel R untuk harga N yang berurutan pada harga A yang sama sehingga diperoleh selisih R yang harganya sama dengan H 1 Rekayasa Trafik, Sukiswo 17

Menghitung harga b 4 Dengan cara yang serupa dengan cara menghitung H, maka b dapat dihitung dengan cara berikut – b=[ A/ N]B; bila N 2=N 3=NAlt (sehingga b 2 = b 3 = b), maka : • Untuk N=NAlt didapat A 1=f(NAlt)B • Untuk N=NAlt+1 didapat A 2=f(NAlt+1)B • Maka b=A 2 -A 1 Rekayasa Trafik, Sukiswo 18

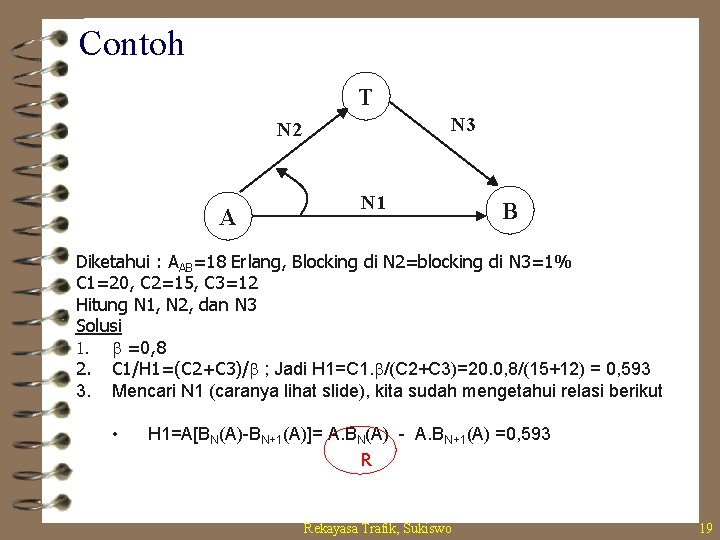
Contoh T N 3 N 2 A N 1 B Diketahui : AAB=18 Erlang, Blocking di N 2=blocking di N 3=1% C 1=20, C 2=15, C 3=12 Hitung N 1, N 2, dan N 3 Solusi 1. b =0, 8 2. C 1/H 1=(C 2+C 3)/b ; Jadi H 1=C 1. b/(C 2+C 3)=20. 0, 8/(15+12) = 0, 593 3. Mencari N 1 (caranya lihat slide), kita sudah mengetahui relasi berikut • H 1=A[BN(A)-BN+1(A)]= A. BN(A) - A. BN+1(A) =0, 593 R Rekayasa Trafik, Sukiswo 19

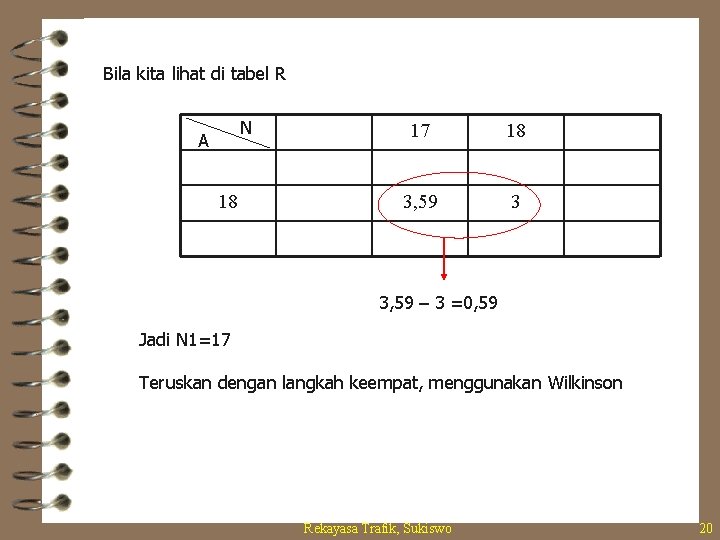
Bila kita lihat di tabel R N A 18 17 18 3, 59 3 3, 59 – 3 =0, 59 Jadi N 1=17 Teruskan dengan langkah keempat, menggunakan Wilkinson Rekayasa Trafik, Sukiswo 20

4 Pratt mendasarkan perhitungan pada struktur jaringan segitiga yang sederhana, tetapi sebetulnya semakin kompleks struktur jaringannya, makin kompleks pula cara menghitungnya Rekayasa Trafik, Sukiswo 21

Optimasi menurut Y. Rapp 4 Prinsipnya sama dengan Pratt 4 Harga H didekati oleh suatu parameter yang disebut improvement factor 4 Simbol improvement factor : F(n, A) 4 F(n, A) memiliki pengertian yang sama dengan H (marginal occupancy): pertambahan trafik yang dapat dimuat pertambahan saluran 4 F(n, A)=e[1 -0, 3(1 -e 2)]; dimana e : cost ratio Rekayasa Trafik, Sukiswo 22

Optimasi menurut Y. Rapp (2) 4 F(n, A) juga dapat dihitung oleh persamaan berikut ini F(n, A) = A[En(A)-En+1(A)]=he h memiliki harga sekitar 0, 6 -0, 9 • h sama dengan b pada Pratt 4 Cost ratio=e=Cd/Ca – Cd = cost untuk direct route – Ca = cost untuk rute alternatif 4 Jadi relasi antara Y. Rapp dengan Pratt H =(Cd/Ca)b=F(n, A)=e[1 -0, 3(1 -e 2)] =A[En(A)-En+1(A)]=he Rekayasa Trafik, Sukiswo 23

Optimasi menurut Y. Rapp (3) 4 Sebagai patokan praktis, dapat digunakan hubungan berikut : – Bila (C 2+C 3)/C 1 < 1 , maka N 1 = 0 – Bila 1 < (C 2+C 3)/C 1 2 , maka N 1 A – Bila (C 2+C 3)/C 1 > 2 maka harga N 2 = N 3 = 0 4 C 2 dan C 3 : cost pada rute alternatif 4 C 1: cost direct route Rekayasa Trafik, Sukiswo 24

Evaluasi NNGOS dengan metoda Gaudreau 4 Diperkenalkan pertama kali oleh Manon Gaudreau pada majalah IEEE Communication, Vol. 28, No. 3, bulan Maret tahun 1980 4 Diperluas oleh W. S. Chan Rekayasa Trafik, Sukiswo 25

Evaluasi NNGOS dengan metoda Gaudreau (2) 4 Asumsi-asumsi – Tidak boleh ada trafik yang melalui sentral yang sama sampai 2 kali – Antara sentral paling sedikit harus ada satu rute – Tak ada pengulangan panggilan – Untuk setiap pasangan asal-tujuan, fungsi luap T harus ada berkas terkahir (final link) – Probabilitas blocking dari berkas saluran tak bergantungan – Probabilitas blocking dari berkas hanya merupakan fungsi dari berkas termaksud saja Rekayasa Trafik, Sukiswo 26

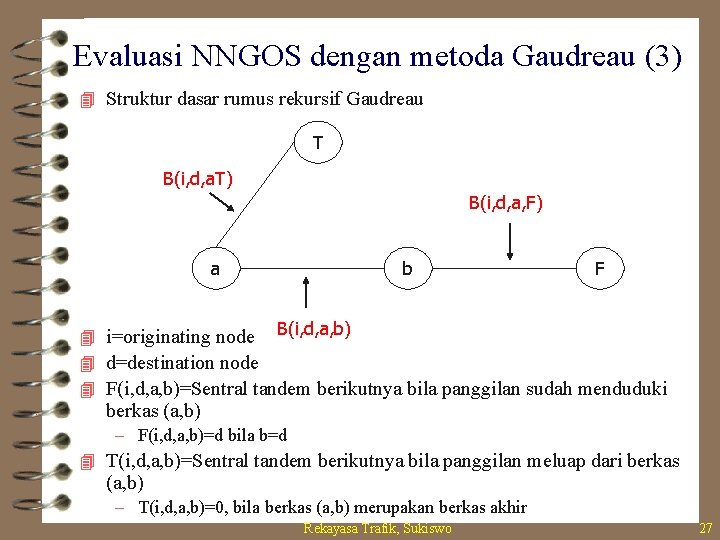
Evaluasi NNGOS dengan metoda Gaudreau (3) 4 Struktur dasar rumus rekursif Gaudreau T B(i, d, a. T) B(i, d, a, F) a b F 4 i=originating node B(i, d, a, b) 4 d=destination node 4 F(i, d, a, b)=Sentral tandem berikutnya bila panggilan sudah menduduki berkas (a, b) – F(i, d, a, b)=d bila b=d 4 T(i, d, a, b)=Sentral tandem berikutnya bila panggilan meluap dari berkas (a, b) – T(i, d, a, b)=0, bila berkas (a, b) merupakan berkas akhir Rekayasa Trafik, Sukiswo 27

Evaluasi NNGOS dengan metoda Gaudreau (4) 4 F disebut Forward Matrix 4 T disebut Overflow Matrix 4 Bila P(a, b) adalah probabilitas blocking dari berkas (a, b) dan B(i, d, a, b) merupakan probabilitas blocking dari sentral a ke d melalui semua rute yang dikembangkan dari F(i, d, a, b) dan T(i, d, a, b) atau dengan perkataan lain, panggilan sudah sampai sentral a dan berkas berikutnya yang dicoba untuk diduduki adalah berkas (a, b), maka …(next slide) Rekayasa Trafik, Sukiswo 28

Evaluasi NNGOS dengan metoda Gaudreau (5) 4 Bila probabilitas blocking di sentral diabaikan B(i, d, a, b) = 0 ; bila a = d 1 ; bila a d dan b = 0 {1 -P(a, b)}. B(i, d, b, F(i, d, a, b)) + P(a, b). B(i, d, a, T(i, d, a, b)) ; bila a d dan b 0 4 Bila probabilitas blocking di sentral cukup besar 0 ; bila a = d 1 ; bila a d dan b = 0 B(i, d, a, b) = (1 -W 0 a)(1 -P(a, b)). [(1 -Wib). B(i, d, b, F(i, d, a, b))+ Wib] +[(1 -W 0 a). P(a, b)+ W 0 a]. B(i, d, a, T(i, d, a, b)) ; bila a d dan b 0 – Wxi = probabilitas kongesti untuk incoming di sentral x – Woi = probabilitas kongesti untuk outgoing di sentral x Rekayasa Trafik, Sukiswo 29

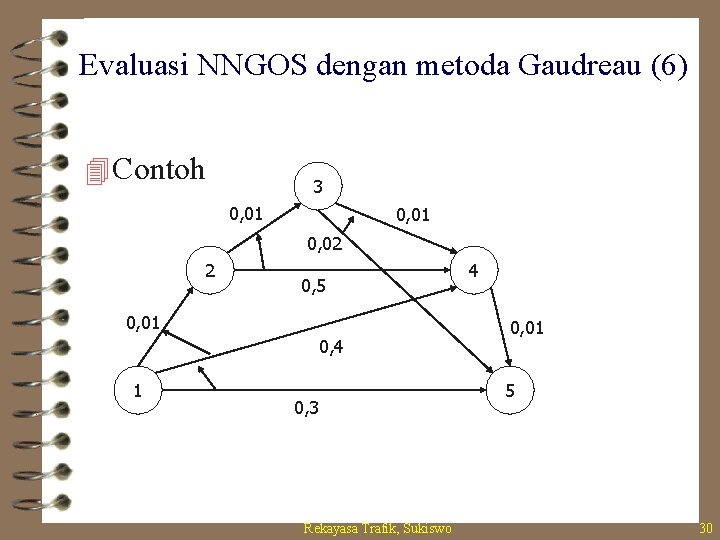
Evaluasi NNGOS dengan metoda Gaudreau (6) 4 Contoh 3 0, 01 0, 02 2 0, 5 0, 01 0, 4 1 0, 3 Rekayasa Trafik, Sukiswo 4 0, 01 5 30

Evaluasi NNGOS dengan metoda Gaudreau (7) 4 Solusi F= 0 0 0 4 0 0 0 5 5 5 0 0 5 5 0 T= -1 -1 -1 0 -1 -1 2 3 0 -1 -1 4 0 -1 Untuk matriks F, bila tidak berkas maka beri nilai 0 Untuk matriks T, bila tidak ada berkas maka beri nilai -1 P= 0, 000 1, 000 1, 000 0, 010 0, 000 1, 000 0, 400 0, 500 0, 010 0, 000 1, 000 0, 300 1, 000 0, 020 0, 010 0, 000 Untuk matriks P, bila tidak berkas maka beri nilai 1 Rekayasa Trafik, Sukiswo 31

Evaluasi NNGOS dengan metoda Gaudreau (8) 4 Iterasi perhitungan NNGOS – B(1, 5, 1, 5)=(1 -P 15). B(1, 5, 5, F(1, 5, 1, 5))+P 15. B(1, 5, 1, T(1, 5, 1, 5)) =(1 -0, 3). B(1, 5, 5, 5)+0, 3. B(1, 5, 1, 4) =0 – – =0, 3. B(1, 5, 1, 4)=(1 -P 14). B(1, 5, 4, F(1, 5, 1, 4))+P 14. B(1, 5, 1, T(1, 5, 1, 4)) =(1 -0, 4). B(1, 5, 4, 5)+0, 4. B(1, 5, 1, 2) B(1, 5, 4, 5)=(1 -P 45). B(1, 5, 5, F(1, 5, 4, 5))+P 45. B(1, 5, 4, T(1, 5, 4, 5)) =(1 -0, 1). B(1, 5, 5, 5)+0, 01. B(1, 5, 4, 0) =1 =0, 01. 1=0, 01 Dan seterusnya, sampai akhirnya anda memperoleh hasil B(1, 5, 1, 5) = 0, 004211 Rekayasa Trafik, Sukiswo 32

Beberapa parameter kinerja jaringan 4 Go. S (Grade of Service) 4 ASR (Answered Seizure Ratio) 4 SCH (Seizure per Circuit per Hour) 4 MHT (Mean Holding Time per Seizure) 4 SCR (Succesfull Call Ratio) Rekayasa Trafik, Sukiswo 33

ASR 4 ASR = Jumlah Call Answered Jumlah Call Seizure x 100% 4 ASR SLJJ (diukur di sentral toll) Kota A Answered Seizure TE TE Toll Exchange LE Local Exchange Call seizure: outgoing call dari suatu sentral toll ke arah sentral toll lain 4 ASR Lokal – Diukur di sentral toll Answered Seizure TE LE Rekayasa Trafik, Sukiswo 34

4 ASR Lokal (2) – Diukur di sentral lokal Answered Seizure LE LE Call seizure: outgoing call dari suatu sentral lokal ke sentral lokal lain dalam suatu multi exchange area 4 Hasil pengukuran ASR diperingkatkan mulai dari yang tertinggi sampai terendah 4 Prioritas pembenahan mulai dari urutan ASR terendah Rekayasa Trafik, Sukiswo 35

SCR (Succesful Call Ratio) 4 Macam-macam loss – Loss originating (tingkat pemanggil) • Kegagalan karena : no dialling, incomplete dialling, invalid dialling, wrong prefix – Loss terminatting (tingkat pemanggil) • Kegagalan karena : yang dipanggil sibuk, yang dipanggil tak menjawab (no answer) – Loss di sentral • Kegagalan karena : tidak berhasilnya proses penyambungan di sentral selain Loss originating (dihitung terhadap call yang masuk ke sentral) – Loss di berkas saluran • Kegagalan karena : tidak berhasil menduduki saluran di berkas salurantermaksud (dihitung terhadap call yang ditawarkan ke berkas yang bersangkutan) Rekayasa Trafik, Sukiswo 36

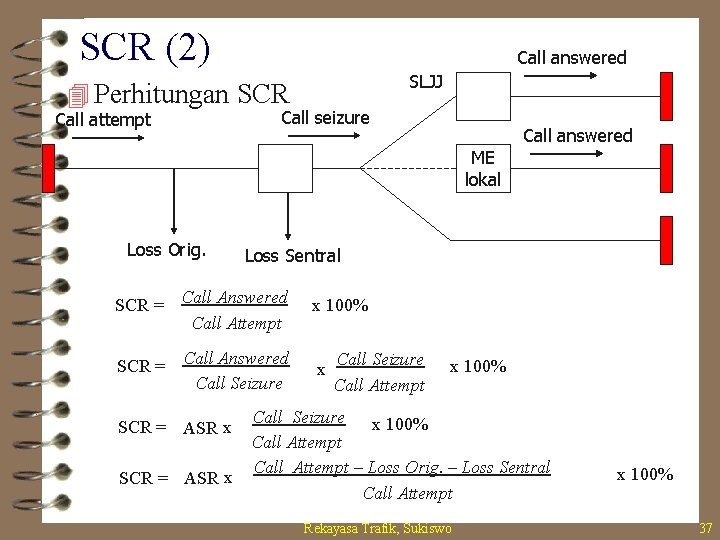
SCR (2) Call answered SLJJ 4 Perhitungan SCR Call attempt Call seizure Call answered ME lokal Loss Orig. Loss Sentral SCR = Call Answered Call Attempt x 100% SCR = Call Answered Call Seizure x SCR = ASR x Call Seizure Call Attempt x 100% Call Seizure x 100% Call Attempt – Loss Orig. – Loss Sentral Call Attempt Rekayasa Trafik, Sukiswo x 100% 37
![SCR 3 4 Jadi SCR ASR x 1 LoLe SCR Lokal ME SCR (3) 4 Jadi SCR = ASR x [1 -Lo-Le] – SCR Lokal ME](https://slidetodoc.com/presentation_image_h/1d6a6fd3afa05fda78f6209582dbbddb/image-38.jpg)
SCR (3) 4 Jadi SCR = ASR x [1 -Lo-Le] – SCR Lokal ME = ASR(lokal ME)[1 -Lo-Le] – SCR SLJJ= ASR(SLJJ)[1 -Lo-Le] – SCR Internasional= ASR(Internasional)[1 -Lo-Le] ={(Call Term-Loss Term)/Call Term}x Lo-Le] = (1 -Lt) [1 -Lo-Le] Rekayasa Trafik, Sukiswo [1 - 38

Occupancy per Circuit (OCC) 4 OCC=Total holding time/jumlah sirkit 4 OCC : efisiensi sirkit Rekayasa Trafik, Sukiswo 39