Pencil GP notebook assignment red pen If you

Pencil, GP notebook, assignment, red pen If you flipped a quarter, dime, and penny at the same time, how many possible outcomes (heads or tails) are there? Make an organized list or create a tree diagram. Use “H” to represent heads and “T” to represent tails. HHH HHT HTH HTT THH THT TTH TTT +1 each total:

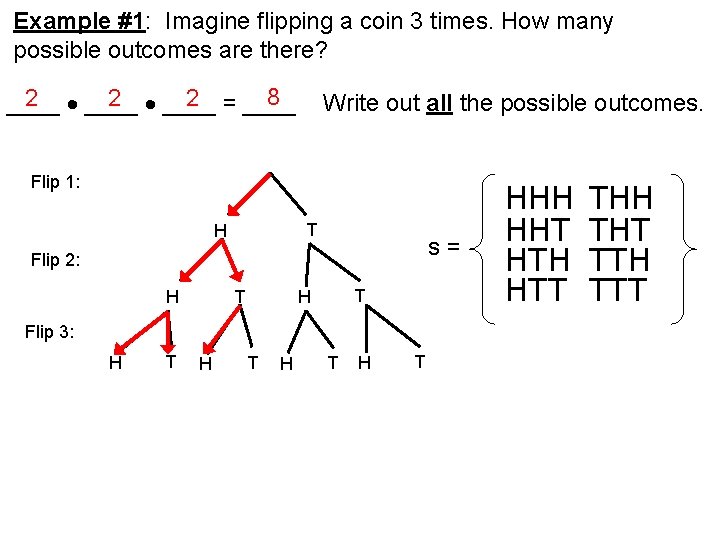
Example #1: Imagine flipping a coin 3 times. How many possible outcomes are there? 8 2 ____ 2 = ____ Write out all the possible outcomes. Flip 1: T H s= Flip 2: H T T H Flip 3: H T H T HHH HHT HTH HTT THH THT TTH TTT

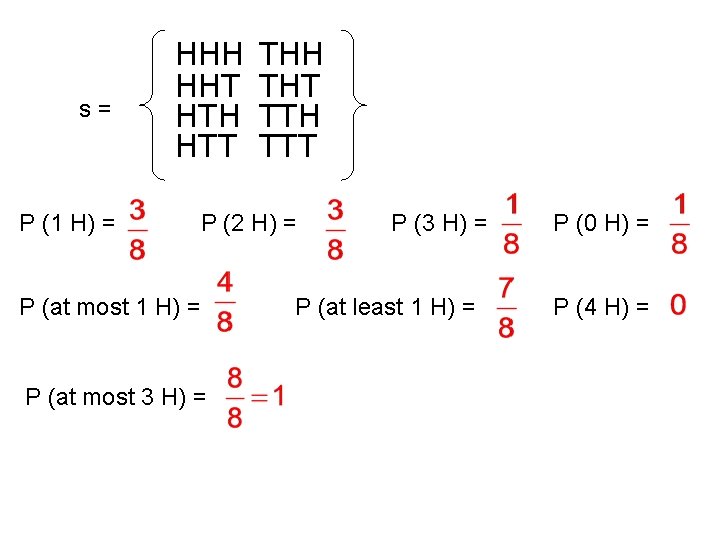
s= P (1 H) = HHH HHT HTH HTT THH THT TTH TTT P (2 H) = P (at most 1 H) = P (at most 3 H) = P (at least 1 H) = P (0 H) = P (4 H) =

CONDITIONAL PROBABILITY finding A given that B has already happened. P(A | B) means __________________ denominator of The number of ways B occurs is the new _______ the probability. Practice #1: a) P (3 H | all same) = b) P (3 H | at least 1 H) = c) P (2 H | at least 1 H) = d) P (2 H | not all tails) = s= HHH HHT HTH HTT THH THT TTH TTT

CONDITIONAL PROBABILITY finding A given that B has already happened. P(A | B) means __________________ denominator of The number of ways B occurs is the new _______ the probability. Practice #1: a) P (3 H | all same) = b) P (3 H | at least 1 H) = c) P (2 H | at least 1 H) = d) P (2 H | not all tails) = notice these say the same thing s= HHH HHT HTH HTT THH THT TTH TTT

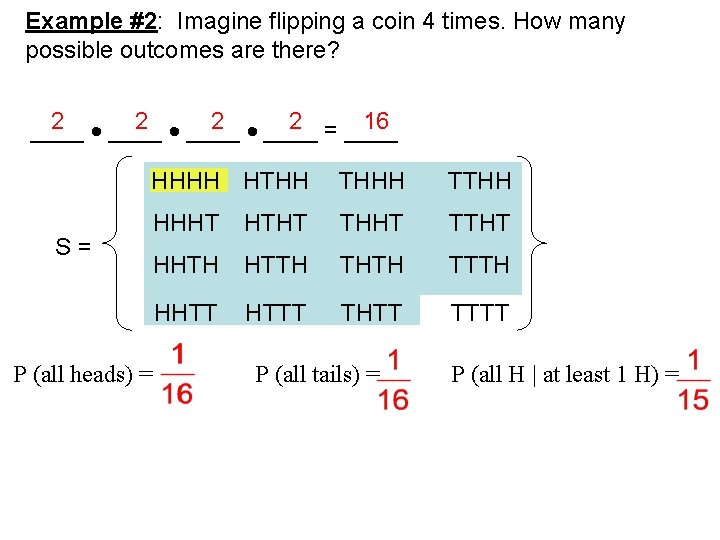
Example #2: Imagine flipping a coin 4 times. How many possible outcomes are there? 2 ____ 2 = ____ 16 ____ HHHH HTHH THHH TTHH HHHT HTHT THHT TTHT HHTH HTTH THTH TTTH HHTT HTTT THTT TTTT S= P (all heads) = P (all tails) = P (all H | at least 1 H) =

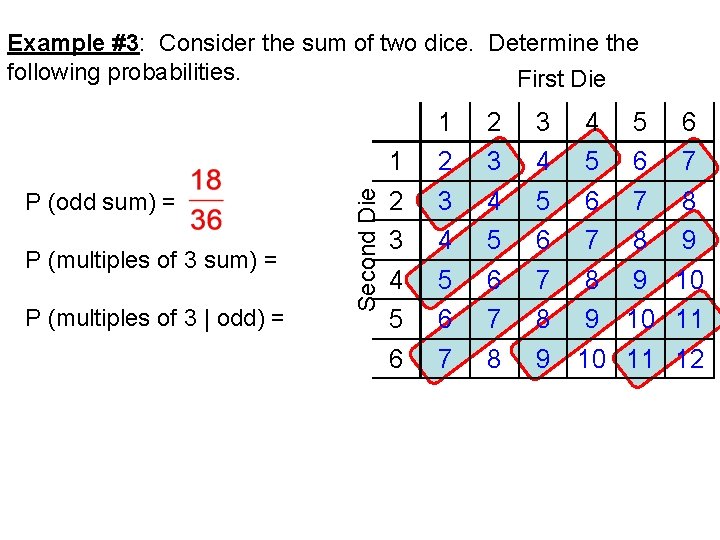
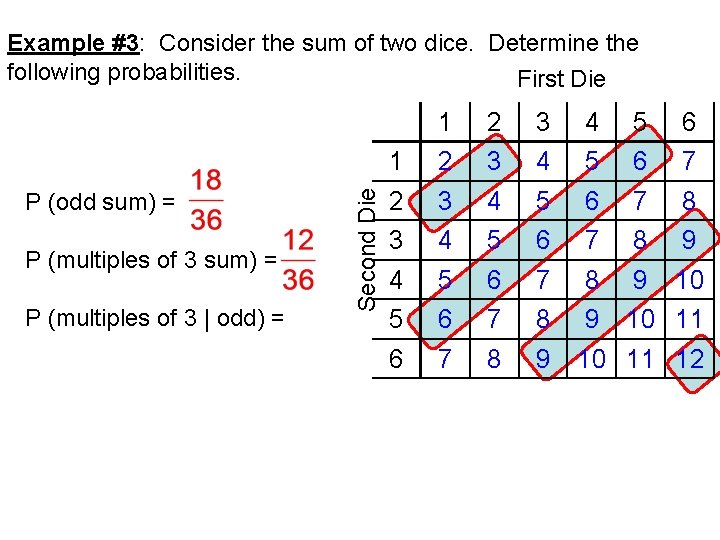
P (odd sum) = P (multiples of 3 | odd) = Second Die Example #3: Consider the sum of two dice. Determine the following probabilities. First Die 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12

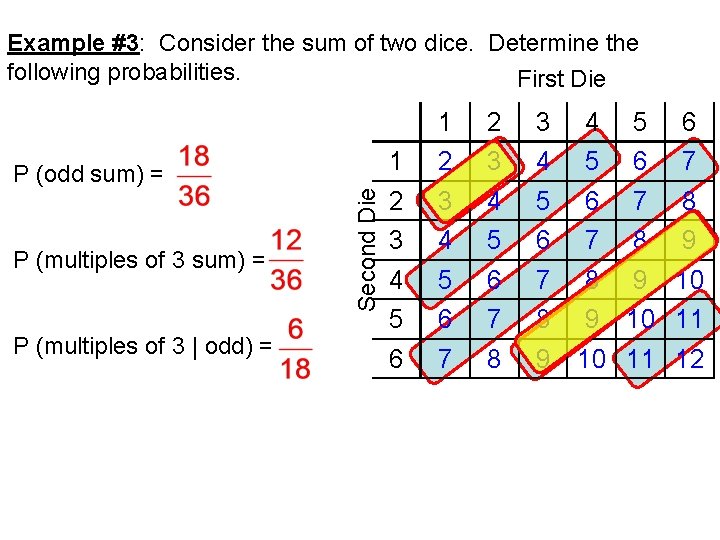
Example #3: Consider the sum of two dice. Determine the following probabilities. First Die P (multiples of 3 sum) = P (multiples of 3 | odd) = Second Die P (odd sum) = 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12

Because we have an area model, this probability is easy to visualize. You will not always have an area diagram so…. There is a rule for conditional probability. P (A | B) = P (A and B) probability of both A and B happening at the same time P (B) probability of B Let A = multiples of 3 B = odd sums. P(multiple of 3 and odd) = ______ P (A | B) = __________ P(odd) A sample space= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Yes, this is more complicated, but it’s “technical” way of solving conditional probabilities. 6, 6, 6 12 both A and B B 5, 5, 5, 5 3, 3 9, 9, 9 7, 7, 7, 7 , 9 11, 11

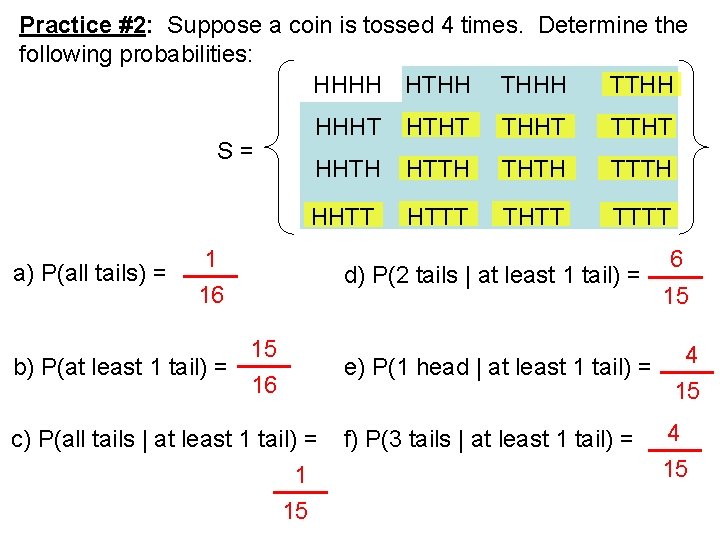
Practice #2: Suppose a coin is tossed 4 times. Determine the following probabilities: HHHH HTHH THHH TTHH S= a) P(all tails) = HHHT HTHT THHT TTHT HHTH HTTH THTH TTTH HHTT HTTT THTT TTTT 1 16 15 b) P(at least 1 tail) = 16 c) P(all tails | at least 1 tail) = 1 15 d) P(2 tails | at least 1 tail) = e) P(1 head | at least 1 tail) = f) P(3 tails | at least 1 tail) = 6 15 4 15

Practice #3: Consider a deck of 52 playing cards. Determine the following probabilities. Recall that there are: 4 suits (♠, ♣, ♥, ♦) ♥ and ♦ are red, ♠ and ♣ are black 13 cards in each suit (2, 3, 4, four of each type of card 5, 6, 7, 8, 9, 10, J, Q K, A) (e. g. , four 2’s, four 3’s) a) P (♦ | red) = c) P (J♥ | J) = 13 26 1 4 b) P (J | face card) = d) P (4 | not face card) = 4 12 4 40

Complete today’s assignment: Worksheet, PM 61, 62, 64, 67 Remember: Quiz #1 tomorrow!!!