PEMILIHAN JENIS LENGKUNG GEOMETRIK JALAN Jurusan Teknik Sipil






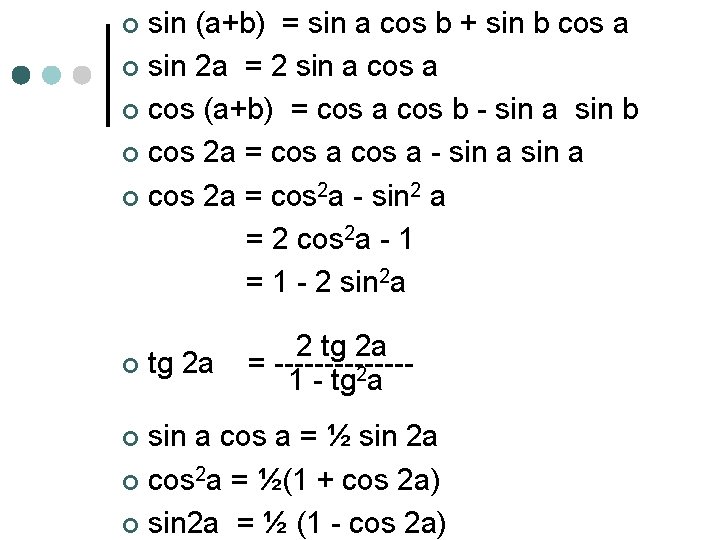


































- Slides: 74

PEMILIHAN JENIS LENGKUNG GEOMETRIK JALAN Jurusan Teknik Sipil dan Lingkungan Fakultas Teknik, Universitas Gadjah Mada

Alinemen HORIZONTAL - - Alinemen horisontal adalah proyeksi sumbu jalan pada bidang horisontal Alinemen horisontal sering disebut juga dengan situasi jalan atau “trase jalan” Alinemen horisontal tersusun dari garis lurus yang disebut tangen dan bagian lengkung yang disebut tikungan Alinemen jalan lengkap juga menunjukkan data-data tikungan, jenis pekerjaan utama dan garis kebebasan samping, serta bangunan-bangunan yang ada di jalan

Alinemen HORIZONTAL TIPE-TIPE ALINEMEN -FULL –CIRCLE -SPIRAL-CIRCLE-SPIRAL - SPIRAL

Bagian Tikungan Bagian tikungan jalan harus dapat memebuhi n Mengimbangi gaya sentrifugal n Daerah bebas pandang disamping Bentuk: – – – n Full circle Spiral Circle Spiral-Spiral Superelevasi, e – e. MAX = 8% atau 10%

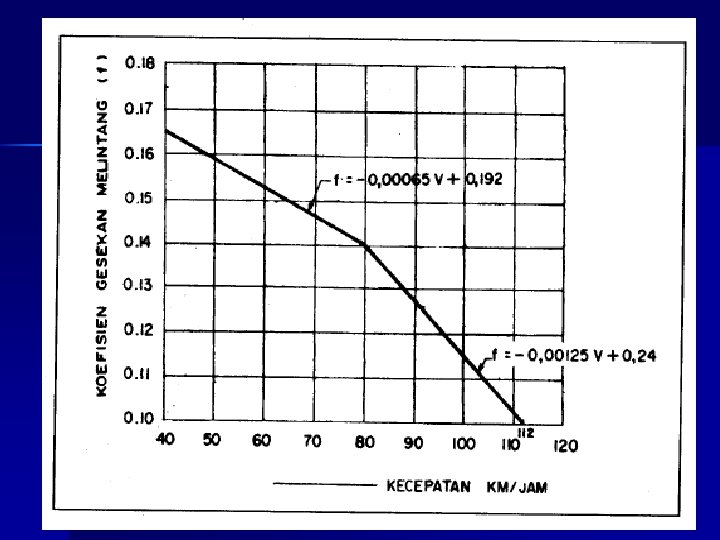
Panjang jari-jari tikungan minimum, Rmin n Rmin = VR 2 / {127 (emax + f )} – f = 0, 14 – 0, 24 – emax = superelevasi max VR (Km/Jam) 120 100 80 60 50 40 30 20 R min (m) 600 370 210 115 80 50 30 15


Bentuk Lengkung Horizontal Garis lengkung dapat terdiri dari: • Busur lingkaran saja (Full-Circle). • Busur lingkaran dan busur peralihan (Spiral. Circle-Spiral), • Busur peralihan saja (Spiral-Spiral),

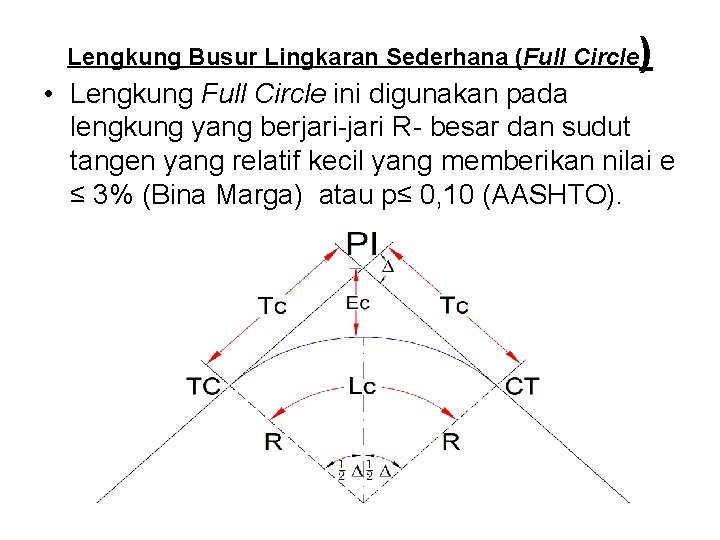
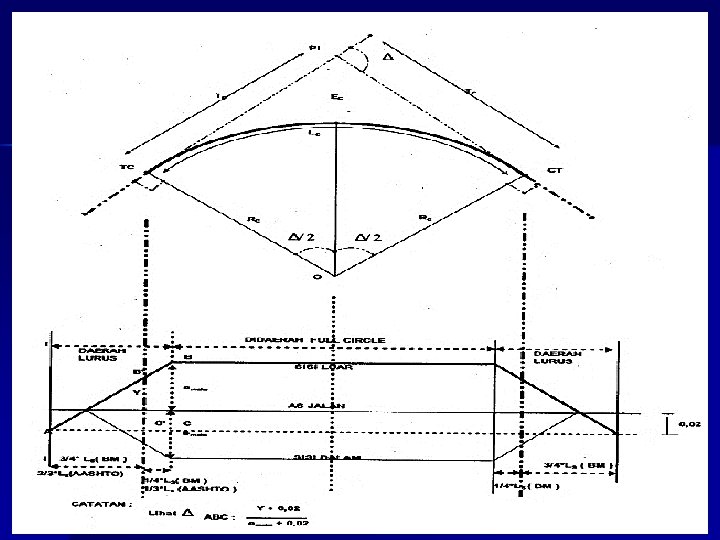
Lengkung Busur Lingkaran Sederhana (Full Circle ) • Lengkung Full Circle ini digunakan pada lengkung yang berjari-jari R- besar dan sudut tangen yang relatif kecil yang memberikan nilai e ≤ 3% (Bina Marga) atau p≤ 0, 10 (AASHTO).
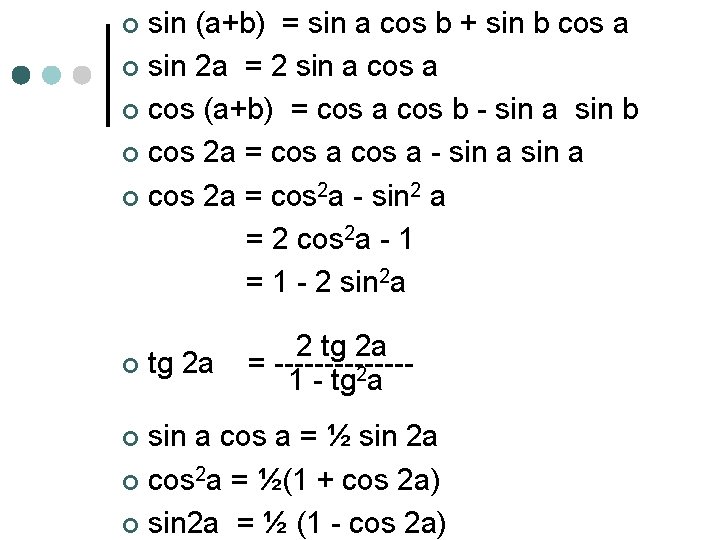
sin (a+b) = sin a cos b + sin b cos a ¢ sin 2 a = 2 sin a cos a ¢ cos (a+b) = cos a cos b - sin a sin b ¢ cos 2 a = cos a - sin a ¢ cos 2 a = cos 2 a - sin 2 a = 2 cos 2 a - 1 = 1 - 2 sin 2 a ¢ 2 tg 2 a ¢ tg 2 a = ------- 1 - tg 2 a sin a cos a = ½ sin 2 a ¢ cos 2 a = ½(1 + cos 2 a) ¢ sin 2 a = ½ (1 - cos 2 a) ¢

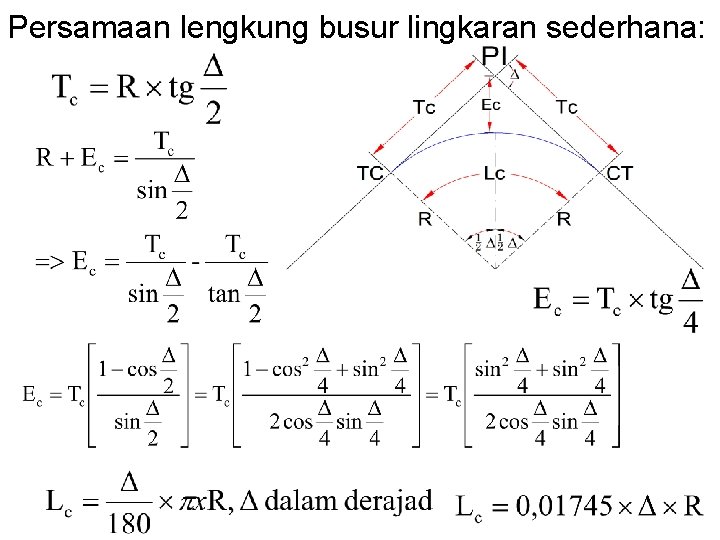
Persamaan lengkung busur lingkaran sederhana:

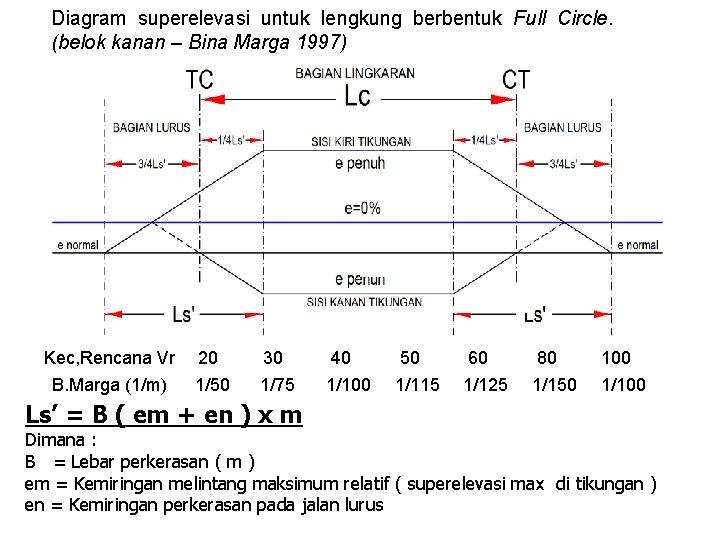
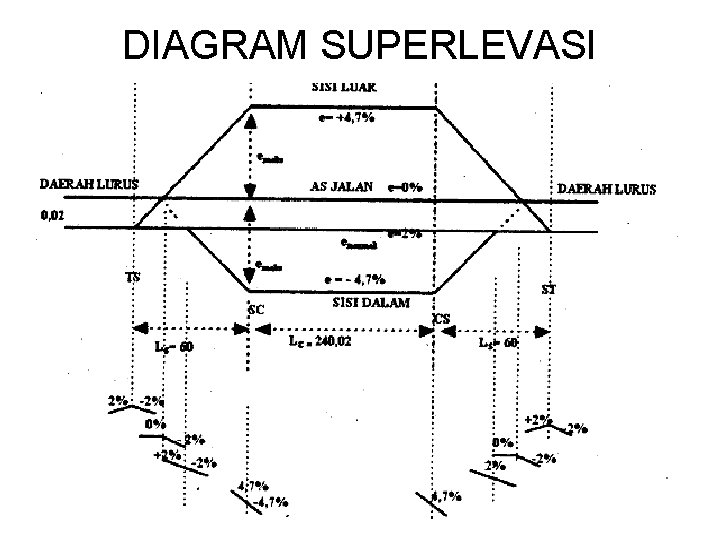
Diagram superelevasi untuk lengkung berbentuk Full Circle. (belok kanan – Bina Marga 1997) Kec, Rencana Vr 20 B. Marga (1/m) 1/50 30 40 50 60 80 100 1/75 1/100 1/115 1/125 1/150 1/100 Ls’ = B ( em + en ) x m Dimana : B = Lebar perkerasan ( m ) em = Kemiringan melintang maksimum relatif ( superelevasi max di tikungan ) en = Kemiringan perkerasan pada jalan lurus





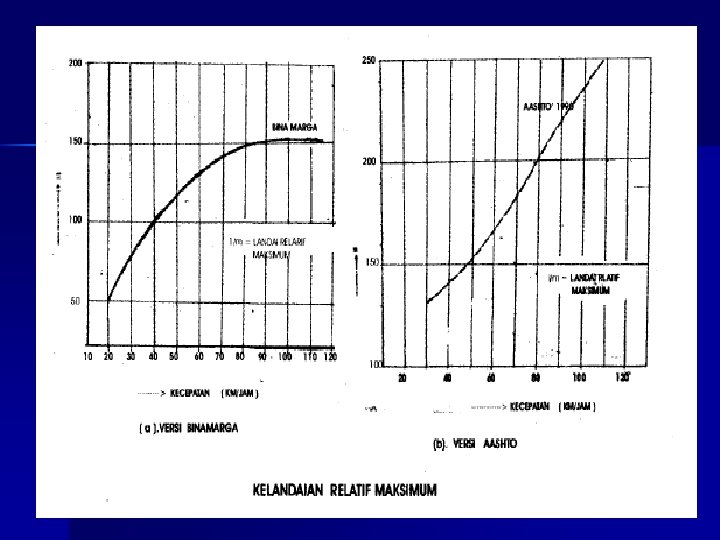
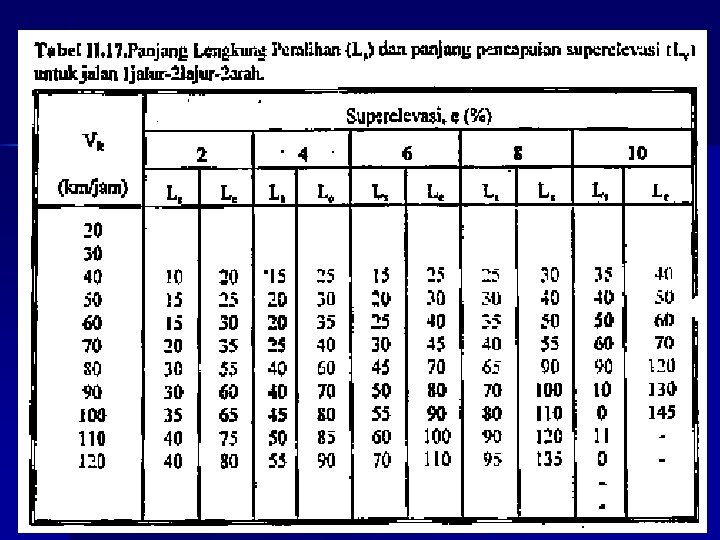
Lengkung peralihan n Sisipan antar bagian lurus dan lengkung Bentuk Spiral atau Parabola Panjang lengkung peralihan, LS ditetapkan: – Waktu tempuh max 3 detik – Antisipasi gaya sentrifugal – Tingkat perubahan kelandaian re-max n n VR <80 Km/jam, re-max = 0, 035 m/m/detik VR ≥ 80 Km/jam, re-max = 0, 025 m/m/detik – Gunakan tabel LS



ANALISIS SHORT


Panjang lengkung peralihan (Ls) yang digunakan dalam perencanaan adalah yang terpanjang dari pemenuhan persyaratan untuk: • Kelandaian relatif maksimum Modifikasi rumus SHORT Berdasarkan panjang perjalanan selama waktu tempuh 3 detik (Bina Marga) atau 2 detik (AASHTO)= Ls = (V/3. 6). T No Kecepatan Rencana (Vr) 20 30 Bina Marga 1/50 1/75 No Kecepatan Rencana (Vr) AASHTO 40 50 60 80 100 1/100 1/115 1/125 1/150 1/100 32 48 64 80 88 96 104 1/33 1/150 1/175 1/200 1/213 1/222 1/244




Ringkasan Rumus LS (pilih LS terpanjang dari 3 rumus) 1. 2. 3. LS = (VR /3, 60) T LS = 0, 022 VR 3/(R. C) – 2, 727 VR. E / C LS = (emax-en) VR / (3, 60 re) • • • T = waktu tempuh lengkung peralihan ( 3 detik) VR =Kecepatan rencana, Km/jam C = perubahan percepatan(0. 4)atau 0. 1 - 1 m/detik 3 R =iari-jari tikungan, m En = superelevasi normal, 2% s. d. 2, 5% re = tingkat perubahan capaian superelevasi(m/m/detik) n n VR <80 Km/jam, re-max = 0, 035 m/m/detik VR ≥ 80 Km/jam, re-max = 0, 025 m/m/detik


Panjang Jari-jari tikungan tanpa lengkung peralihan, RTLP VR (Km/Jam) 120 100 80 60 50 40 30 20 RTLP (m) 2500 1500 900 500 350 250 130 60

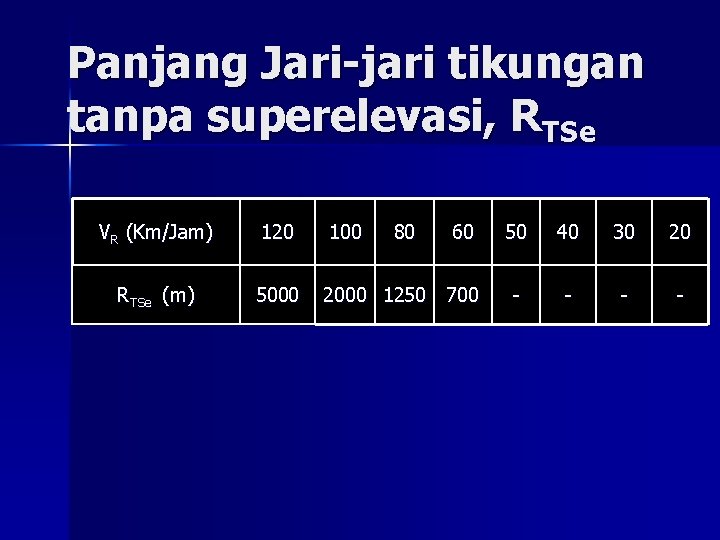
Panjang Jari-jari tikungan tanpa superelevasi, RTSe VR (Km/Jam) 120 100 80 60 RTSe (m) 5000 2000 1250 700 50 40 30 20 - -

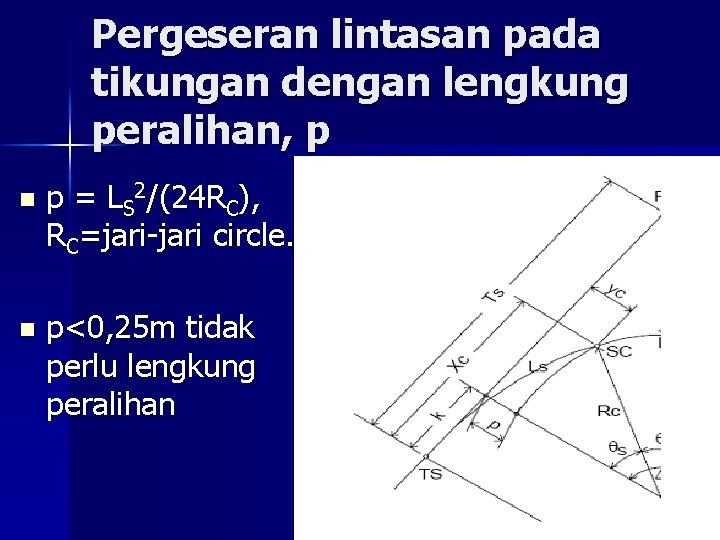
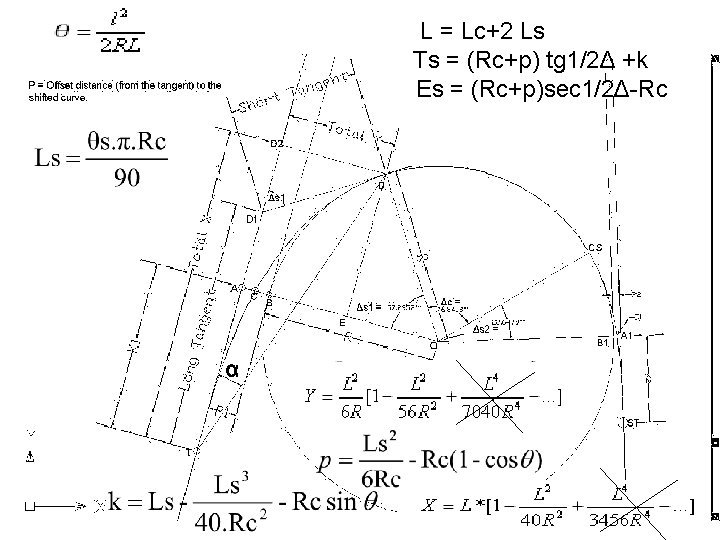
Pergeseran lintasan pada tikungan dengan lengkung peralihan, p n p = LS 2/(24 RC), RC=jari-jari circle. n p<0, 25 m tidak perlu lengkung peralihan

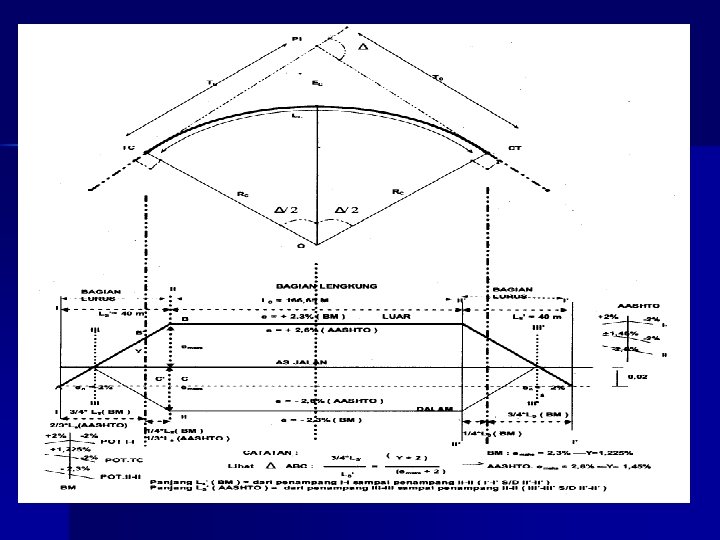
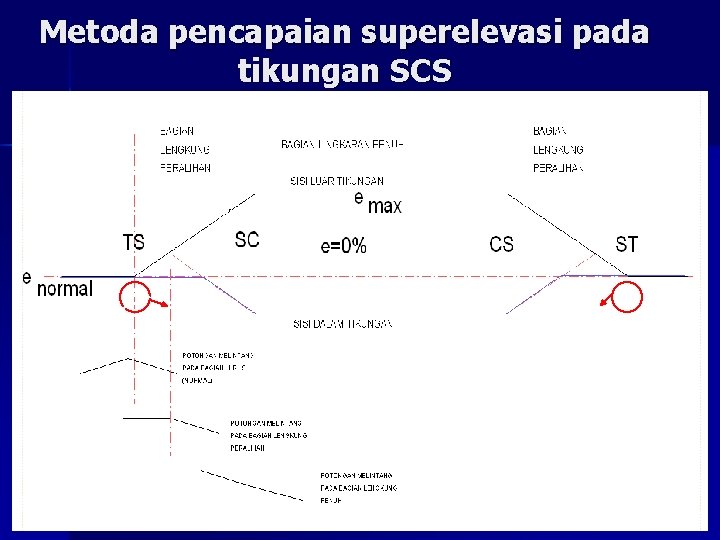
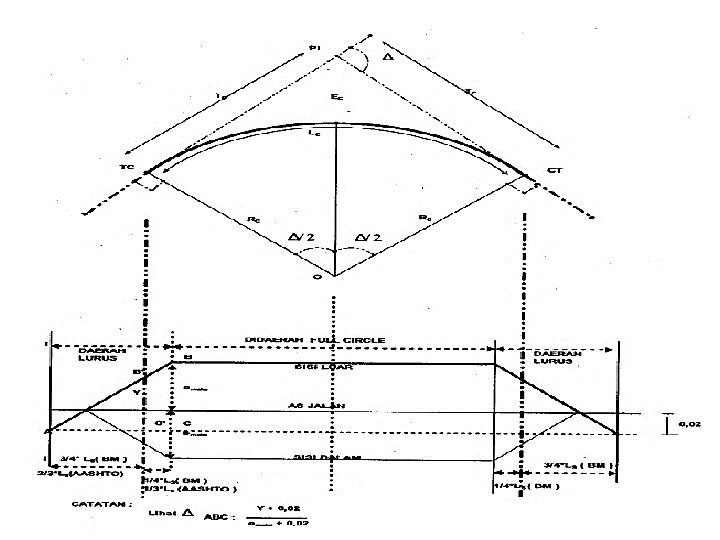
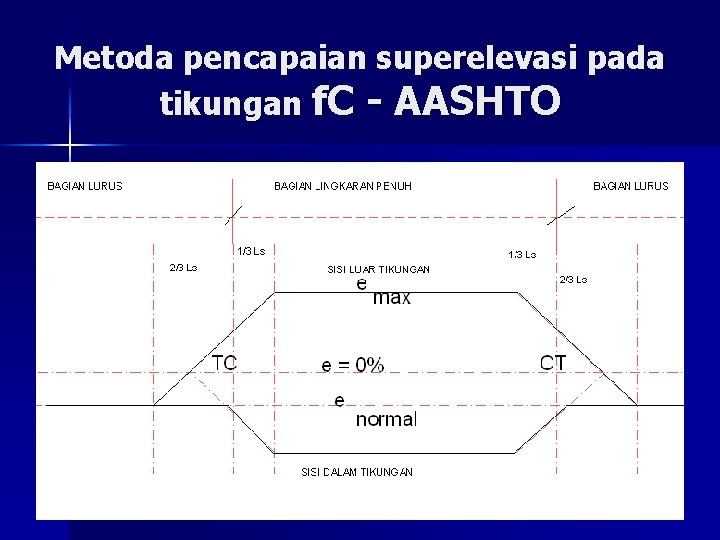
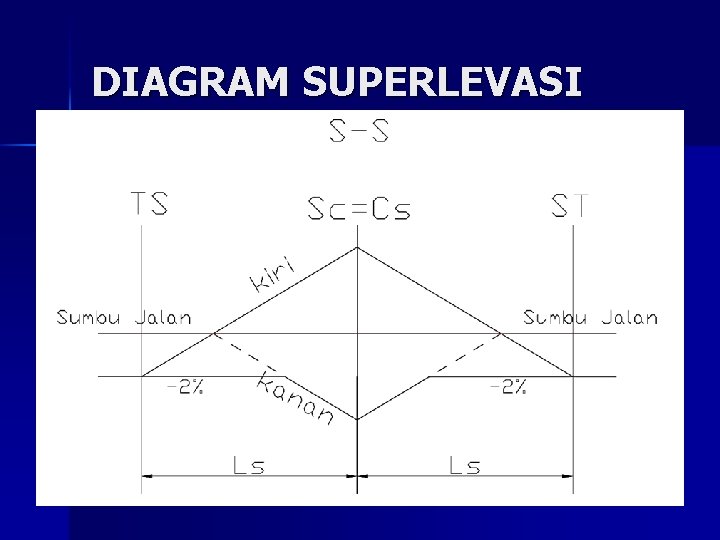
Metoda pencapaian Superelevasi n n Pencapaian secara Linear Pada tikungan SCS: – Dari superelevasi normal pd bagian lurus s. d. TS: dari (2%2, 5%) s. d. (0%) – dari TS s. d. SC: 0% s. d. superelevasi penuh (e%) n Pada tikungan f. C: – Bina Marga 3/4 LS pada bagian lurus 1/4 LS pada bagian Circle – AASHTO 2/3 LS pada bagian lurus 1/3 LS pada bagian Circle n Pada tikungan SS: – Superelevasi seluruhnya dilakukan pada bagian Spiral

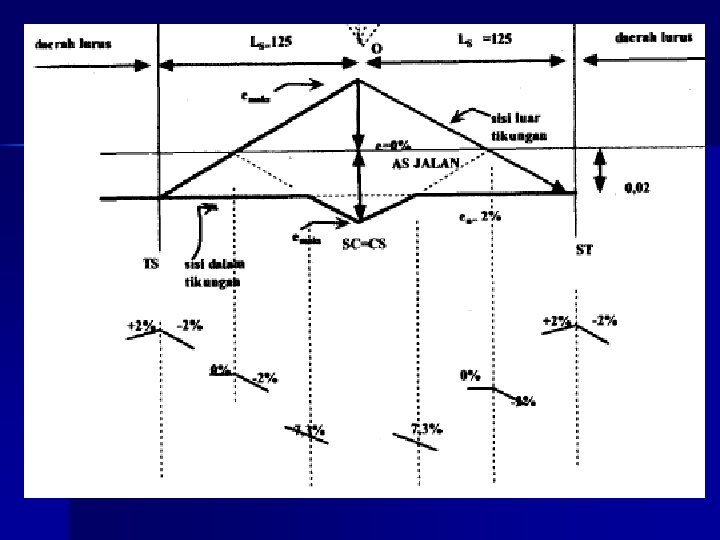
Metoda pencapaian superelevasi pada tikungan SCS


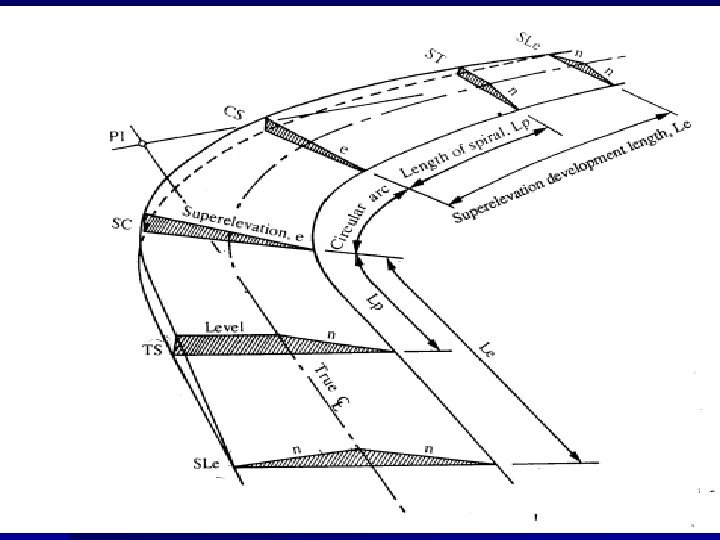
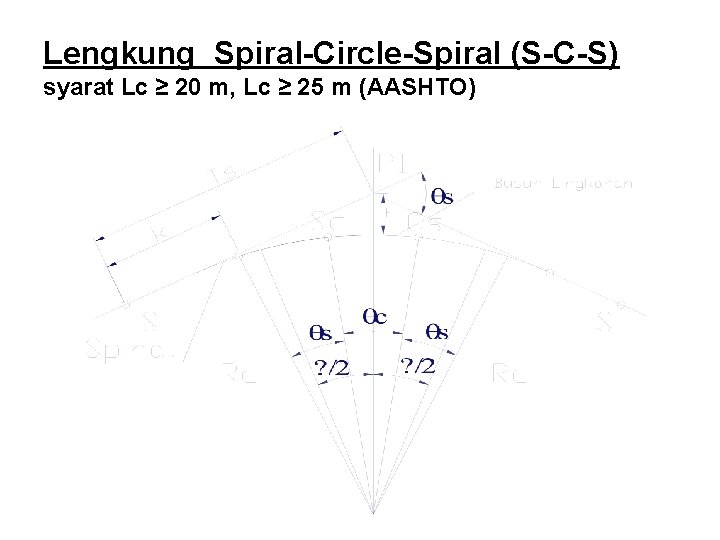
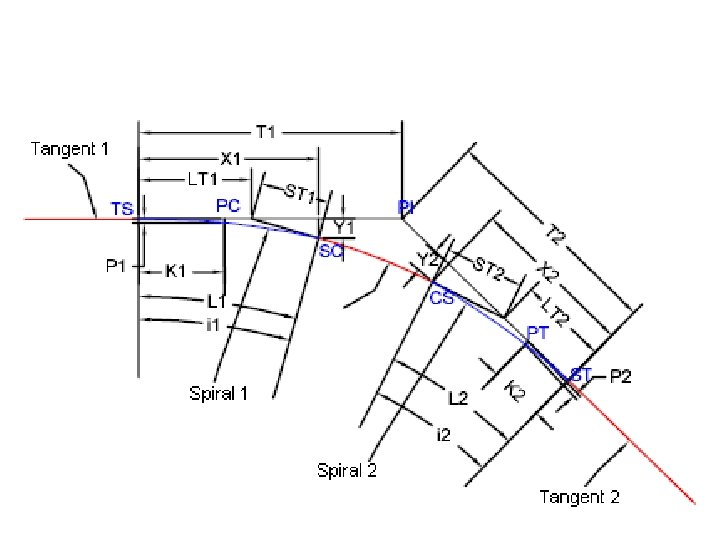
Lengkung Spiral-Circle-Spiral (S-C-S) syarat Lc ≥ 20 m, Lc ≥ 25 m (AASHTO)

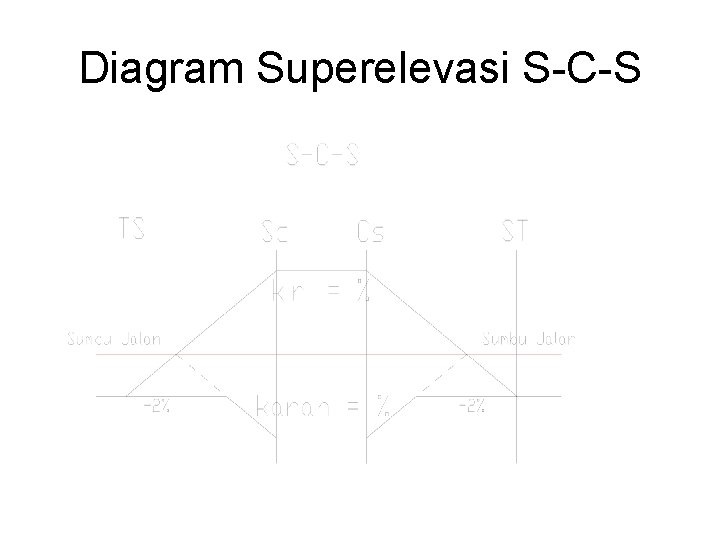
Diagram Superelevasi S-C-S

Persamaan : c = Δ - 2 s SYARAT Lc ≥ 20 m Lc ≥ 25 m Es = (Rc+P)sec 1/2 Δ-Rc 1/m = (e + en). B/Ls Ts = (Rc+P) tg 1/2 Δ+k

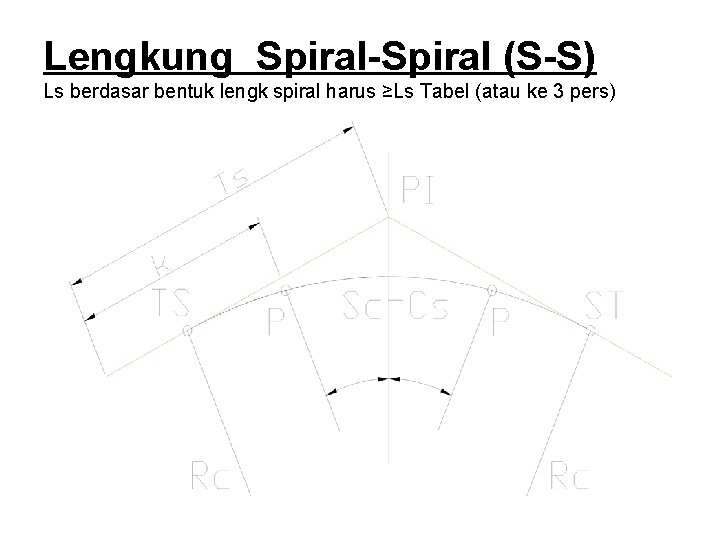
Lengkung Spiral-Spiral (S-S) Ls berdasar bentuk lengk spiral harus ≥Ls Tabel (atau ke 3 pers)

Persamaan : s = ½ Δ (Ls Berdasar bentuk lengkung spiral HARUS > Ls Tabel) L = 2 Ls Ts = (Rc+p) tg 1/2Δ +k Es = (Rc+p)sec 1/2Δ-Rc 1/m = (e + en). B/Ls



L = Lc+2 Ls Ts = (Rc+p) tg 1/2Δ +k Es = (Rc+p)sec 1/2Δ-Rc





DIAGRAM SUPERLEVASI





Metoda pencapaian superelevasi pada tikungan f. C - AASHTO

Diagram Superelevasi S-C-S

DIAGRAM SUPERLEVASI

Panjang lengkung peralihan (Ls) yang digunakan dalam perencanaan adalah yang terpanjang dari pemenuhan persyaratan untuk: • Kelandaian relatif maksimum No Kecepatan Rencana (Vr) 20 30 Bina Marga 1/50 1/75 No Kecepatan Rencana (Vr) AASHTO 40 50 60 80 100 1/100 1/115 1/125 1/150 1/200 32 48 64 80 88 96 104 1/33 1/150 1/175 1/200 1/213 1/222 1/244

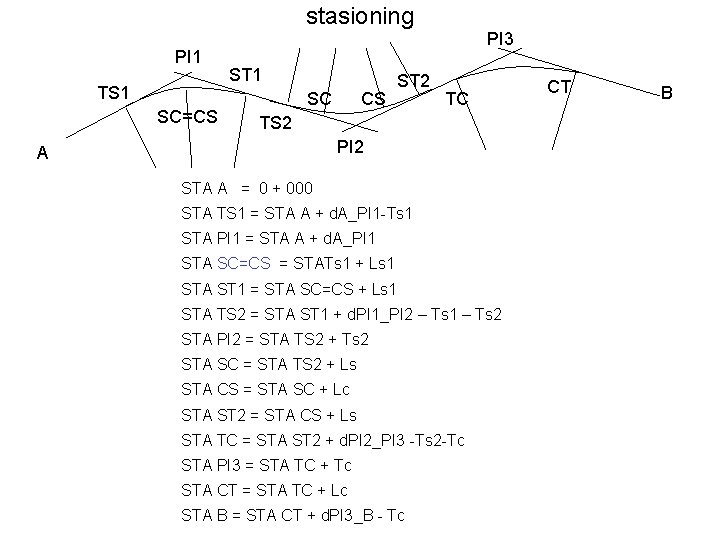
stasioning PI 1 TS 1 SC=CS ST 1 SC CS ST 2 PI 3 TC TS 2 PI 2 A STA A = 0 + 000 STA TS 1 = STA A + d. A_PI 1 -Ts 1 STA PI 1 = STA A + d. A_PI 1 STA SC=CS = STATs 1 + Ls 1 STA ST 1 = STA SC=CS + Ls 1 STA TS 2 = STA ST 1 + d. PI 1_PI 2 – Ts 1 – Ts 2 STA PI 2 = STA TS 2 + Ts 2 STA SC = STA TS 2 + Ls STA CS = STA SC + Lc STA ST 2 = STA CS + Ls STA TC = STA ST 2 + d. PI 2_PI 3 -Ts 2 -Tc STA PI 3 = STA TC + Tc STA CT = STA TC + Lc STA B = STA CT + d. PI 3_B - Tc CT B

• Bagaimana seharusnya nilai fm, harus dihitung ? ? • Apa perbedaan Metode Bina Marga dan AASHTO ? ? • Bagaimana anda tahu kalau pada bentuk lengkung SS nilai Lc pasti 0 ? ? • Mengapa pada contoh perhitungan bentuk lengkung Full Circle mengambil angka 716 meter? Apakah boleh mengambil angka yang lain? ? ? • Apa sebenarnya Ls’ (Ls Fiktif) tersebut , apakah manipestasi Ls fiktif di lapangan sebenarnya? ? • Apakah perhitungan yang didapatkan pada saat merencanakan lengkung harus sesuai pengaplikasiannya di lapangan atau ada toleransi tertentu? ? • Ada berapa jenis tikungan dalam alinemen horisontal? ? • Ada berapa cara hitung Ls dan mana yang dipakai ? ?

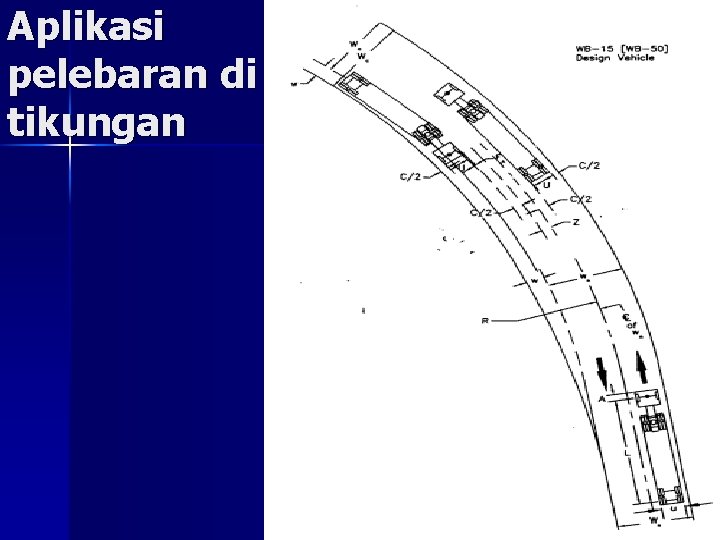
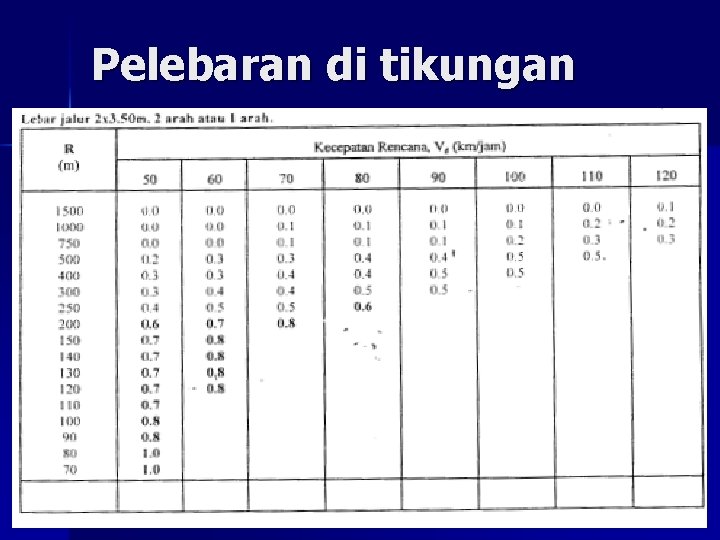
Pelebaran di tikungan n n Konsistensi geometrik, di tikungan sama dgn di bagian lurus Kendaraan harus tetap pada lajurnya Penambahan pelebaran karena gerak melingkar membutuhkan ruang lebih Mengikuti kendaraan rencana Pelebaran <0, 60 m, dapat diabaikan

Aplikasi pelebaran di tikungan

Pelebaran di tikungan

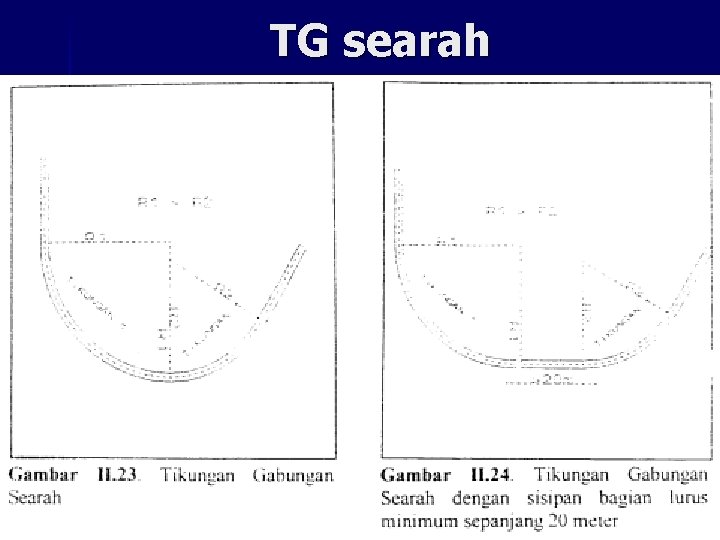
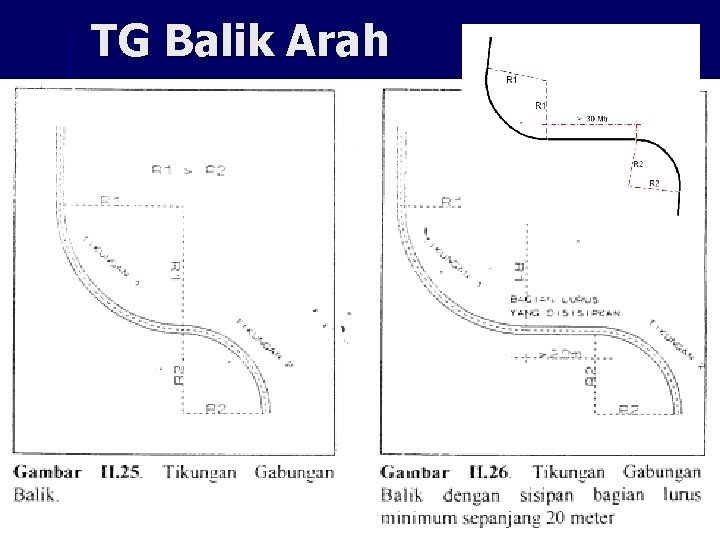
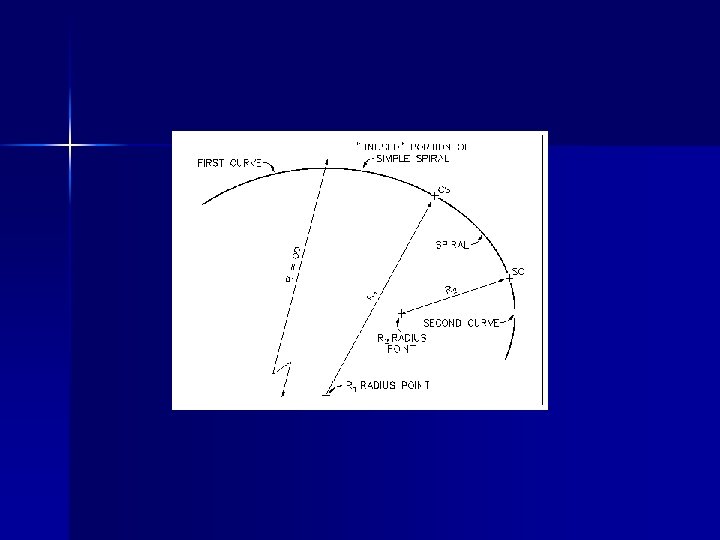
Tikungan Gabungan (TG) n Tipe: – TG searah – TG Balik Arah n n n R 1/R 2 ≥ 2/3, TG searah harus dihindari R 1/R 2 < 2/3, TG harus dilengkapi bagian lurus (atau clothoide) sepanjang ≥ 20 m Setiap TG Balik arah HARUS dilengkapi bagian lurus sepanjang ≥ 30 m

TG searah

TG Balik Arah


Clothoid Spiral While Auto. CAD Civil 3 D supports several spiral types, the clothoid spiral is the most commonly used spiral type. The clothoid spiral is used world wide in both highway and railway track design. First investigated by the Swiss mathematician Leonard Euler, the curvature function of the clothoid is a linear function chosen such that the curvature is zero (0) as a function of length where the spiral meets the tangent. The curvature then increases linearly until it is equal to the adjacent curve at the point where the spiral and curve meet. Such an alignment provides for continuity of the position function and its first derivative (local azimuth), just as a tangent and curve do at a Point of Curvature (PC). However, unlike the simple curve, it also maintains continuity of the second derivative (local curvature), which becomes increasingly important at higher speeds.

Formula Clothoid spirals can be expressed as: Flatness of spiral: Total angle subtended by spiral: Tangent distance at spiral-curve point from tangent-spiral point is: Tangent offset distance at spiral-curve point from tangent-spiral point is:

Bloss Spiral Instead of using the clothoid, the Bloss spiral with the parabola of fifth degrees can be used as a transition. This spiral has an advantage over the clothoid in that the shift P is smaller and therefore there is a longer transition, with a larger spiral extension (K). This factor is important in rail design. Formula Bloss spirals can be expressed as: Other key expressions: Tangent distance at spiral-curve point from tangent-spiral point is: Tangent offset distance at spiral-curve point from tangentspiral point is:

Sinusoidal Curves These curves represent a consistent course of curvature and are applicable to transition from 0 through 90 degrees of tangent deflections. However, sinusoidal curves are not widely used because they are steeper than a true spiral and are therefore difficult to tabulate and stake out. Formula Sinusoidal curves can be expressed as: Differentiating with l we get an equation for l/r, where r is the radius of curvature at any given point:

Cosinusoidal Curves Following is the equation for the Cosinusoidal curve Differentiating with l we get equation for 1/r, where r is the radius of curvature at any given point.

Cubic Spiral (JP) This spiral is developed for requirements in Japan. Some approximations of the clothoid have been developed to use in situations to accommodate a small deflection angle or a large radius. One of these approximations, used for design in Japan, is the Cubic Spiral (JP). Formula Cubic Spirals (JP) can be expressed as: Where X = Tangent distance at spiral-curve point from tangentspiral point This formula can also be expressed as: Where θ is central angle the spiral

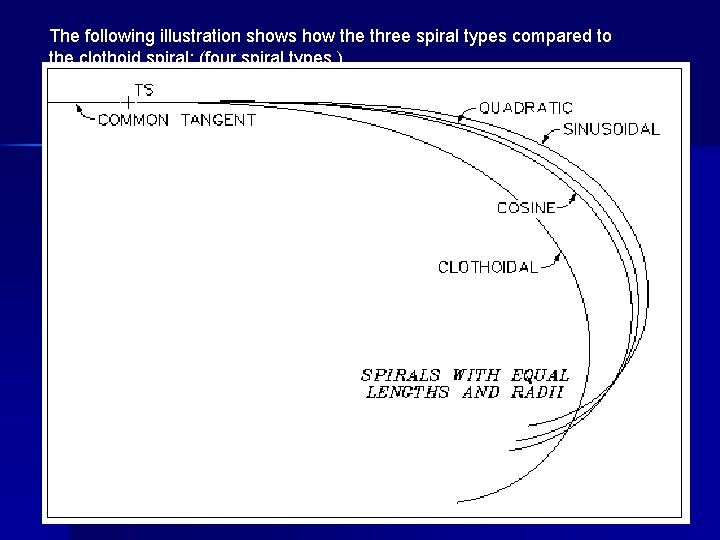
The following illustration shows how the three spiral types compared to the clothoid spiral: (four spiral types )

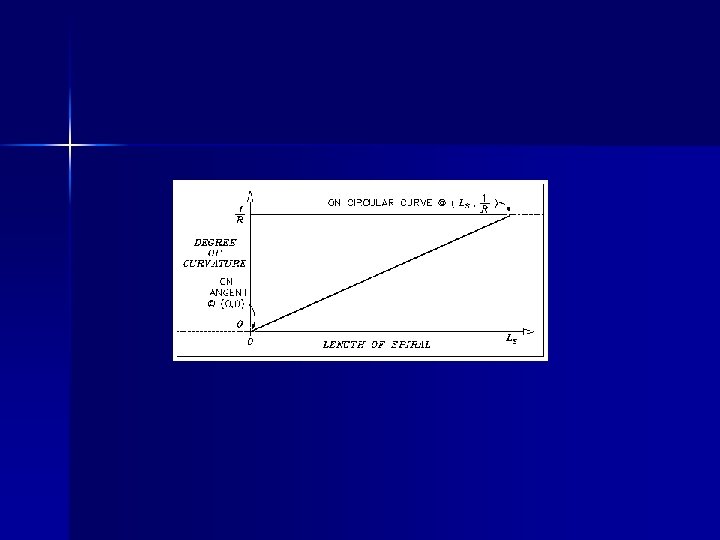
Spiral calculation parameters The following illustration features the clothoid degree of curve function: Clothoid degree of curve function

Quadratic (Schramm) Spirals Quadratic (Schramm) spirals have low values of vertical acceleration. They contain two second-degree parabolas whose radii vary as a function of curve length. Curvature of the first parabola: for Curvature of the second parabola: for This curve is specified by the user-defined length (L) of the transition curve.


