Peculiarities of Angular Distribution of Electrons at New

Peculiarities of Angular Distribution of Electrons at New peculiarities in angular distributions of the <100> Channeling in Silicon Crystal Cherenkov radiation from relativistic heavy New peculiarities in angular distributions of ions the 1, Yu. L. 1, caused by O. V. their stopping inrelativistic radiator: numerical and Bogdanov Pivovarov Cherenkov radiation from heavy ions 2, T. A. 1 theoretical research Y. Takabayashi Tukhfatullin caused by their stopping in radiator: numerical and theoretical research 1 Tomsk 1, O. V. Polytechnic University, Tomsk, E. I. Fiks Bogdanov, Yu. L. Russia Pivovarov 1 1 Tomsk 2 Saga Light Sourse, Japan Polytechnic University, Tomsk, Russia 1

New peculiarities in angular distributions of the Cherenkov radiation from relativistic heavy ions caused by their stopping in radiator: numerical and theoretical research • Introduction: short review on Cherenkov Radiation (Ch. R) theories • Estimation of RHI stopping influence on Ch. R angular distribution • Calculation of Ch. R angular distribution • New features of Ch. R: (L-, z-, λ -, M-dependences) • Conclusions

Introduction Cherenkov radiation (Ch. R) – is an electromagnetic radiation emitted when a charged particle passes through a medium at a velocity greater than the phase velocity of light in that medium: Ch. R is emitted at a specific angle with respect to the straight-line trajectory (or to velocity direction).

Introduction RICH detector = Ring Imaging Cherenkov detector. Combination of 2 effects connected with refractive indices: Ch. R and its reflection by (VUV) mirror. Question: does the width and structure of the ring contain additional information, e. g. on the ion charge ?

Introduction 1. Tamm-Frank (TF) [1], 1934: Theory describing Ch. R of a particle that moves rectilinearly with a constant velocity through a radiator characterized by its refractive index n. Ignores: bending of particle’s trajectory due to multiple scattering (MS) ; decrease of particle’s velocity due to ionization energy loss (slowing-sown effect). 2. Dedrick (D) [2], 1952: Takes into account the influence of the MS on the angular density of the particle’s Ch. R angular distribution. Ignores: slowing-down effect [1] Tamm I. E. , Frank I. M. Doklady AN SSSR, 1937, 14, p. 107. [2] Dedrick K. G. Phys. Rev. , 1952, 87, p. 891.

Introduction 3. Kuzmin & Tarasov (KT) [1], 1993: New model to study Ch. R from a relativistic heavy ions (RHI) moving rectilinearly but with a decreasing velocity through a radiator characterized by its refractive index n. Slowing-down effect plays a key role in forming of the Ch. R angular distribution. Ignores: bending of RHI trajectory due to multiple scattering (MS). KT model is valid only for thin radiators ! [1] Kuzmin E. S, Tarasov A. V. JINR Rapid Communications 4[61]-93 (1993), p. 64.

Introduction 4. Alpatova, Bogdanov, Pivovarov [1], 2009: Developed a new approach which uses the popular computer code SRIM’ 06 to calculate the velocity of an ion depending on its penetration depth in the radiator. The obtained velicoty is substituted into the formula of classical electrodynamics for the spectral-angular distribution of radiation from a charged particle moving in a medium along a trajectory r(t) with taking into account the slowing-down due to ionization energy loss in the radiator. [1] Altapova V. R. , Bogdanov O. V. , Pivovarov Yu. L. // Nuclear Instruments and Methods in Physics Research. 2009. B 256. PP. 109 -113.

Estimation of RHI stopping influence on Ch. R angular distribution Ch. R is emitted at a specific angle (is determined by particle’s velocity) RHI velocity and angle of emitted Ch. R: On entering the radiator: On leaving the radiator: (velocity decreased because of stopping). In [1] was used the following thin radiator approximation for RHI velocity decreasing because of stopping: - stopping power of the radiator width of Ch. R angular distribution (for thin radiator): [1] Kuzmin E. S, Tarasov A. V. JINR Rapid Communications 4[61]-93 (1993), p. 64.

Estimation of RHI stopping influence on Ch. R angular distribution Ch. R is located in a narrow angular interval: -speed of light in vacuum -RHI energy and relativistic factor on entering the radiator After some algebra we finally obtain: may be expressed as: [1] Kuzmin E. S, Tarasov A. V. JINR Rapid Communications 4[61]-93 (1993), p. 64.

Estimation of RHI stopping influence on Ch. R angular distribution To avoid thin radiator approximation: Calculate particle’s velocity in radiator with special known software, e. g. : q. SRIM [1] (The Stopping and Range of Ions in Matter, J. Ziegler) q. ATIMA[2] (developed at GSI, H. Geissel, C. Scheidenberger, P. Malzacher, J. Kunzendorf, H. Weick) : SRIM ATIMA [1] http: //www. srim. org [2] http: //www-linux. gsi. de/~weick/atima/

Calculation of Ch. R angular distribution Intensity of radiation from RHI with a charge Ze penetrating through nonmagnetic dielectric medium characterized by dielectric function (see, e. g. [4]) Tamm-Frank theory Kuzmin & Tarasov Fresnel integrals

Calculation of Ch. R angular distribution Fresnel integrals Stopping-power (Bethe-Bloch formula)

Calculation of Ch. R angular distribution a) b) a): Fine structure of Ch. R angular distribution near θC, TF theory b): New structure and broadening due to stopping in radiator:

New features of Ch. R L-dependence Stopping-power dependence Bethe-Bloch formula Mass-dependence (isotopic effect [5]) λ - dependence

New features of Ch. R (L-dependence) SRIM f(θ, ω), arb. u. Bethe-Bloch 1000 Me. V/u Au Li. F f(θ, ω), arb. u. λ = 390 nm n = 1. 4

New features of Ch. R (z-dependence) SRIM λ = 390 nm n = 1. 4 1000 Me. V/u Ne Li. F λ = 390 nm n = 1. 4 f(θ, ω), arb. u. 1000 Me. V/u Au Li. F f(θ, ω), arb. u. Bethe-Bloch

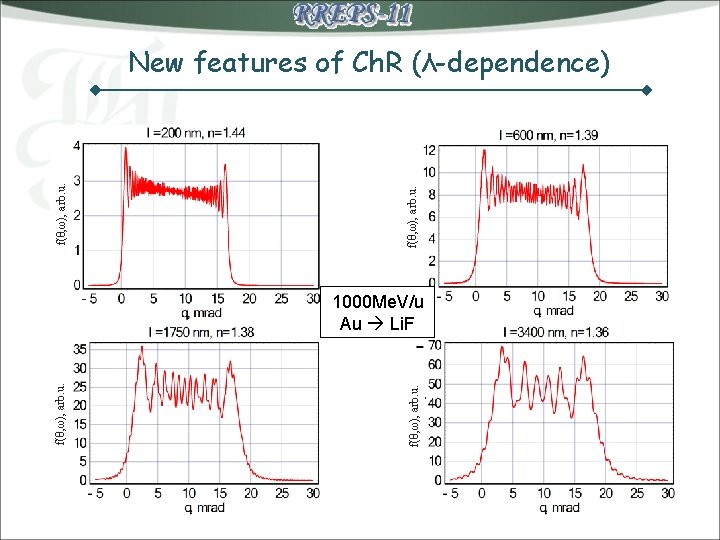
f(θ, ω), arb. u. New features of Ch. R (λ-dependence) 1000 Me. V/u Au Li. F

New features of Ch. R (M-dependence, Isotopic effect) the width and fine structure of the Cherenkov radiation angular distribution in vicinity of the Cherenkov cone are remarkable different for isotopes with different masses, at equal initial relativistic factor (velocity) of isotopes. Example: isotopes with masses M 1, M 2 and equal initial relativistic factors γ 10=γ 20=γ 0 have initial energies E 10(0)= γ 0 M 1 c 2 , E 20(0)= γ 0 M 2 c 2 After a thin layer of radiator Δx both isotopes will lose an equal amount of energy: The next layer of radiator they will enter with different relativistic factors etc. : [1] O. V Bogdanov, Yu. L. Pivovarov. // Il Nuovo Cimento. 2011, in press

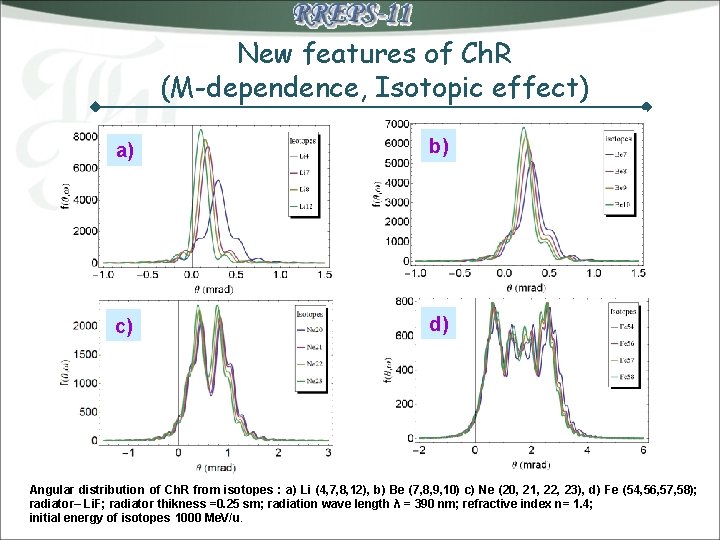
New features of Ch. R (M-dependence, Isotopic effect) a) b) c) d) Angular distribution of Ch. R from isotopes : a) Li (4, 7, 8, 12), b) Be (7, 8, 9, 10) c) Ne (20, 21, 22, 23), d) Fe (54, 56, 57, 58); radiator– Li. F; radiator thikness =0. 25 sm; radiation wave length λ = 390 nm; refractive index n= 1. 4; initial energy of isotopes 1000 Me. V/u.

Conclusions Method to calculate the Ch. R angular distribution based on the thin radiator approximation and a Bethe-Bloch formulae Advantages: Disadvantages: qfast calculation speed qno need to use foreign software qno limits in choosing radiators, ions, energies qis valid only for thin radiators Results of numerical calculations based on Bethe-Bloch formulae and thin radiator approximation are very close to those based on SRIM’ 06.

Conclusions New features: Stopping of RHI in the radiator results in the drastic change of angular distribution of Ch. R in vicinity of the Cherenkov angle. The Ch. R width and fine structure become dependent on: qradiator thickness qwave length qion charge qion mass. Question: does the width and structure of the Cherenkov ring contain additional information, e. g. on the ion charge z? Z- dependence is proved by numerical calculations. q. The experimental studies of predicted effects are possible at existing (GSI) and future (FAIR) accelerators, e. g. using RICH detectors. The possible applications for new features of Ch. R angular distribution width, such as measurements of RHI charge, incident energy, energy loss in the radiator are clearly seen.

Thank you for attention