Pearson Unit 1 Topic 3 Parallel Perpendicular Lines

Pearson Unit 1 Topic 3: Parallel & Perpendicular Lines 3 -3: Proving Lines Parallel Pearson Texas Geometry © 2016 Holt Geometry Texas © 2007

� TEKS Focus: � (5)(C) Use the constructions of congruent segments, congruent angles, angle bisectors, and perpendicular bisectors to make conjectures about geometric relationships. � (1)(G) Display, explain, or justify mathematical ideas and arguments using precise mathematical language in written or oral communication. � (1)(F) Analyze mathematical relationships to connect and communicate mathematical ideas. � (6)(A) Verify theorems about angles formed by the intersection of lines and line segments, including vertical angles, and angle formed by parallel lines cut by a transversal and prove equidistance between the endpoints of a segment and points on its perpendicular bisector and apply these relationships to solve problems.

Basic Terms �Flow Proof—a form of proof in which arrows show the logical connections between the statements

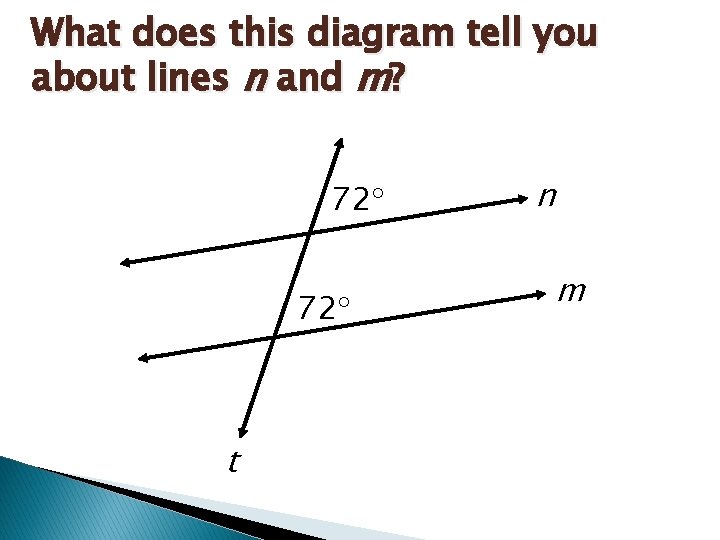
What does this diagram tell you about lines n and m? 72 72 t n m

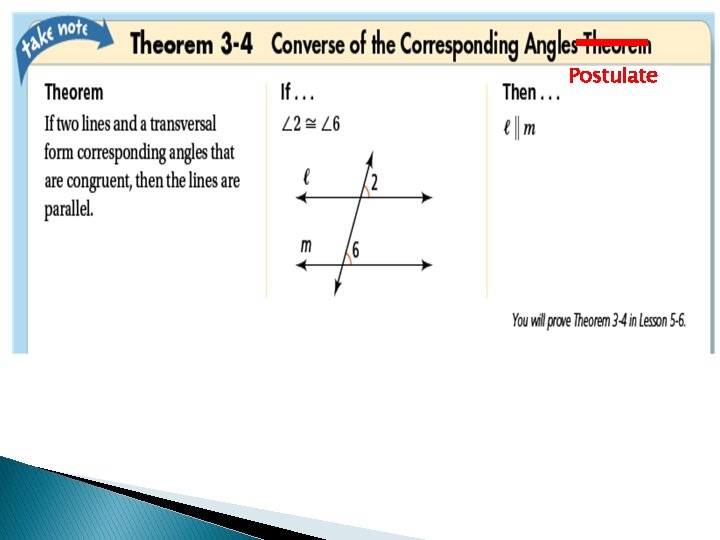
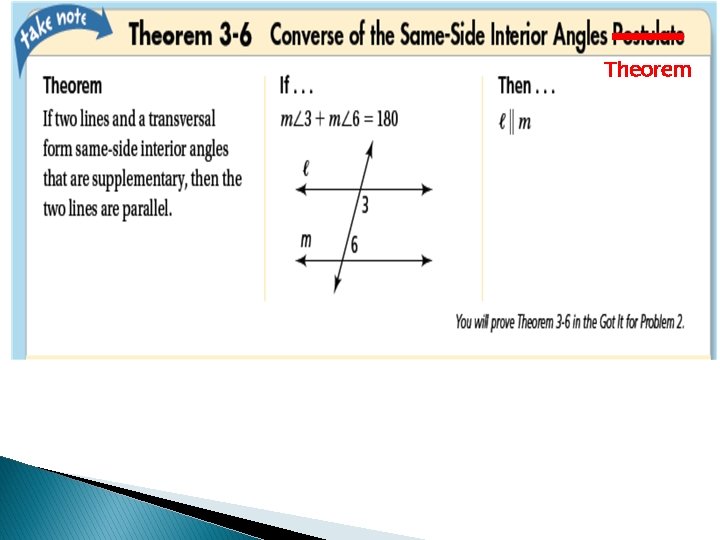
Postulate

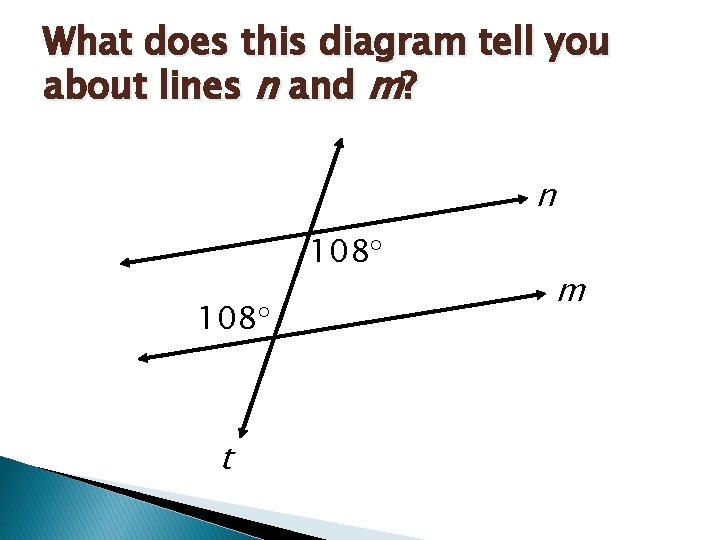
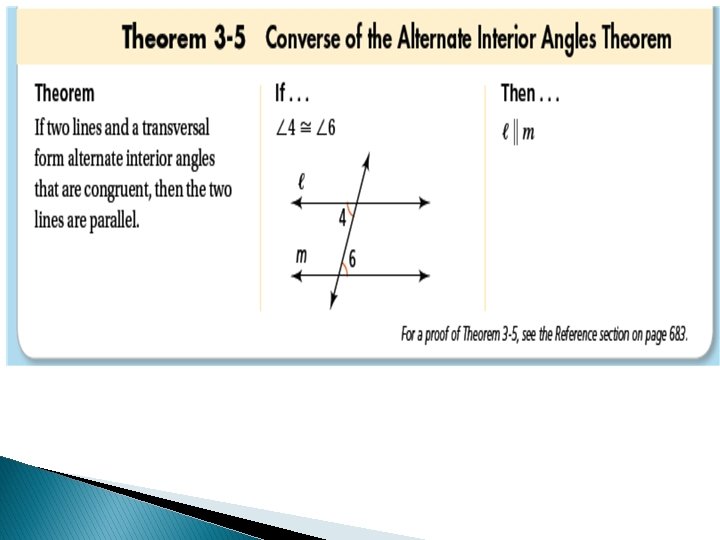
Remember Recall that the converse of a theorem is found by exchanging the hypothesis and conclusion. The converse of a theorem is not automatically true. If it is true, it must be stated as a postulate or proved as a separate theorem.

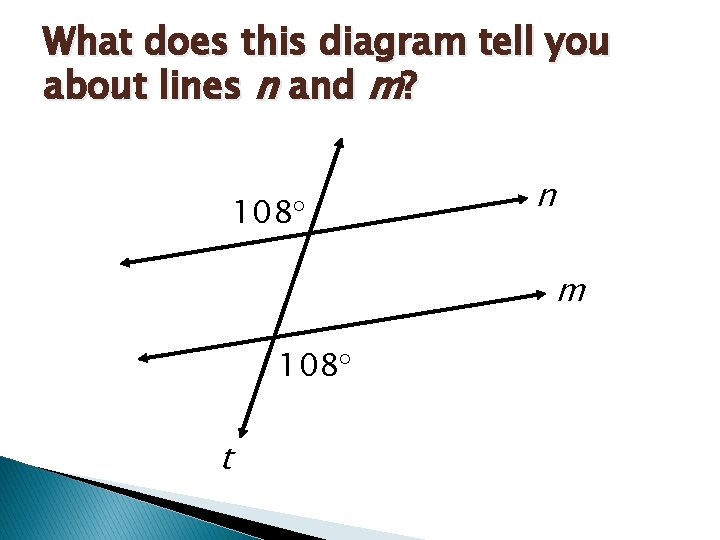
What does this diagram tell you about lines n and m? n 108 t m

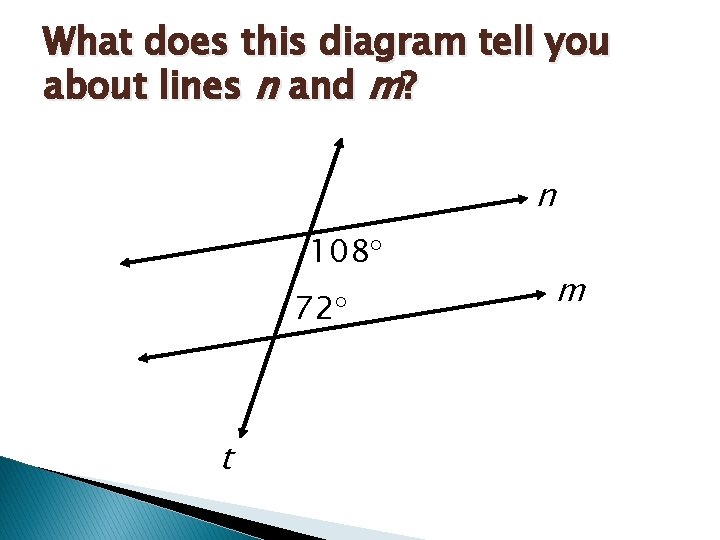
What does this diagram tell you about lines n and m? n 108 72 t m

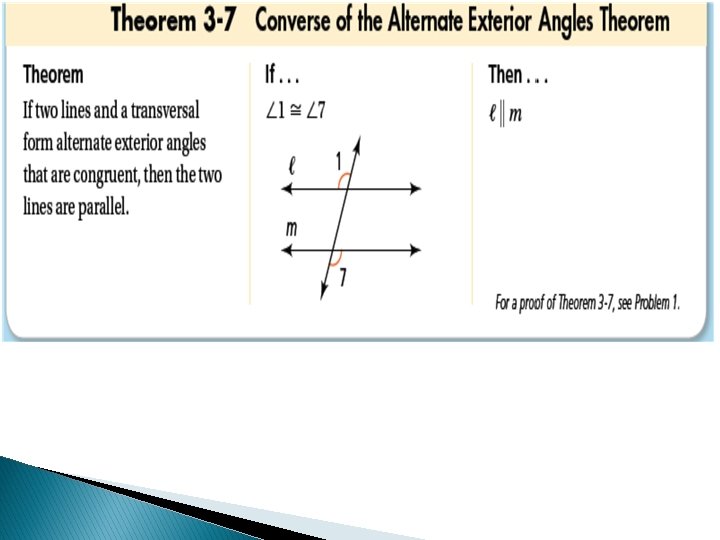
Theorem

What does this diagram tell you about lines n and m? 108 n m 108 t

Proof #1 Use the Converse of the Corresponding Angles Postulate and the given to prove the Alternate Exterior Angles Theorem. Given: ℓ || m Prove: 2 Statements 7 Reasons 1. ℓ || m 1. Given 6 3. 6 7 2. Corr. Angles Post. 3. Vertical Angles Thm. 4. 2 7 4. Transitive Prop. of 2. 2

Proof #2 Use the Converse of the Corresponding Angles Postulate and the given to show that ℓ || m. Given: m 1 = m 3 Prove: ℓ || m Statements Reasons 1. 1 & 3 corresponding angles 1. Def. of Corr. s 2. m 1 = m 3 2. Given 3. 1 3 3. Def. of s. 4. ℓ || m 4. Converse of Corr. s Post.

Proof #3 Refer to the diagram. Use the given information and theorems you have learned to show that r || s. Given: 4 8 Prove: r || s Statements Reasons 1. 4 8 1. Given 2. 4 and 8 are alt. ext. s 2. Def. of alternate ext. s 3. r || s 3. Converse of Alt. Ext. s Thm.

Example: 4 Use the given information and theorems you have learned to show that r || s. Given: m 2 = (10 x + 8)°, m 6 = (25 x – 67)°, x = 5 Prove: r || s m 2 = 10 x + 8 = 10(5) + 8 = 58 m 6 = 25 x – 67= 25(5) – 67 = 58 2 & 6 are alternate interior ’s 2 6 r || s by Converse of Alt. Int. s Theorem

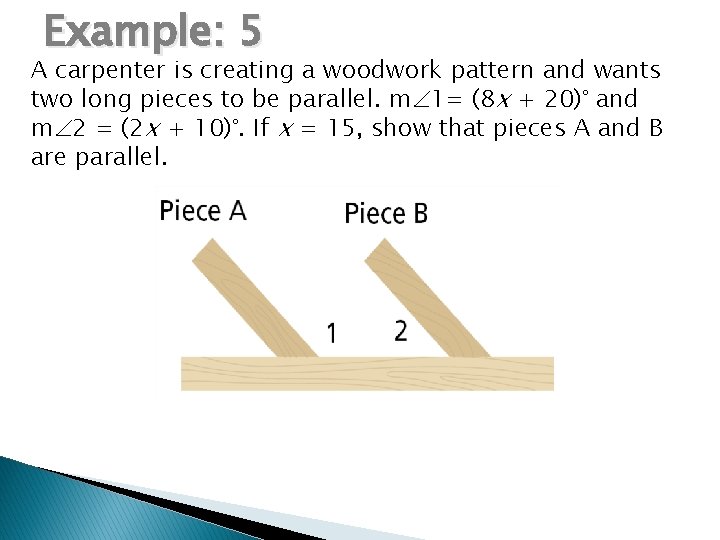
Example: 5 A carpenter is creating a woodwork pattern and wants two long pieces to be parallel. m 1= (8 x + 20)° and m 2 = (2 x + 10)°. If x = 15, show that pieces A and B are parallel.

Example: 5 continued Thoughts: • A line through the center of the horizontal piece forms a transversal to pieces A and B. • 1 and 2 are same-side interior angles. If 1 and 2 are supplementary, then pieces A and B are parallel. • Substitute 15 for x in each expression.

Example: 5 continued m 1 = 8 x + 20 = 8(15) + 20 = 140 m 2 = 2 x + 10= 2(15) + 10 = 40 m 1+m 2 = 140 + 40 = 180 1 & 2 are same-side interior s A || B by Converse of Same Side Int. s

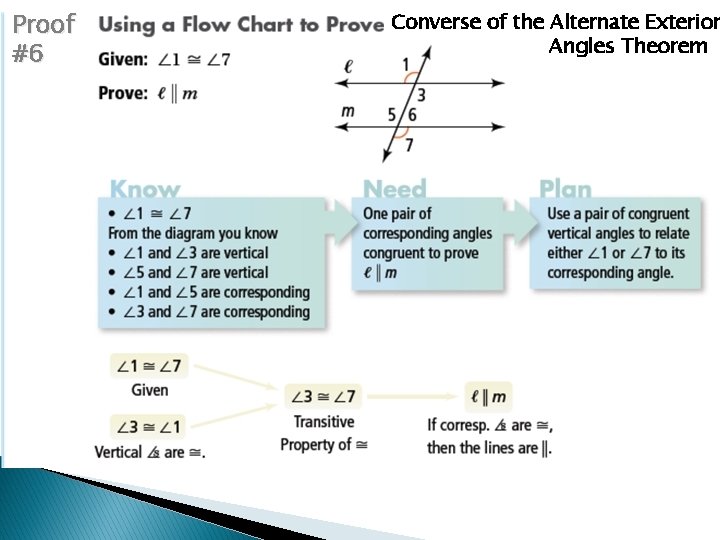
Proof #6 Converse of the Alternate Exterior Angles Theorem

�EXTRA EXAMPLES NOT USED IN COMPOSITION BOOK FOLLOW. �ALSO REMEMBER TO LOG-ON TO YOUR PEARSON ACCOUNT TO LOOK AT OTHER EXAMPLES BEFORE BEGINNING THE ON-LINE HW AND THE WRITTEN HW.

Example: 7 What if…? Suppose the corresponding angles on the same side of the boat measure (4 y – 2)° and (3 y + 6)°, where y = 8. Show that the oars are parallel. 4 y – 2 = 4(8) – 2 = 30° 3 y + 6 = 3(8) + 6 = 30° The angles are congruent, so the oars are || by the Converse of the Corr. s Post.