Pearson Unit 1 Topic 1 Tools of Geometry

Pearson Unit 1 Topic 1: Tools of Geometry 1 -1: Points, Lines, & Planes Pearson Texas Geometry © 2016 Holt Geometry Texas © 2007

�TEKS Focus: �(4)(A) Distinguish between undefined terms, definitions, postulates, conjectures, and theorems. �(1)(D) Communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate. �(1)(F) Analyze mathematical relationships to connect and communicate mathematical ideas.

Videos to watch: � What is a point? � What is a plane?

Basic Terms The most basic figures in geometry are undefined terms, which cannot be defined by using other figures. The undefined terms point, line, and plane are the building blocks of geometry. Building blocks refers to the basic foundation of geometry.

Basic Terms Vocabulary Term Diagram Point Line Plane X A C Definition (use capital letters to name points) A point names a location and has no size. It is represented by a dot. P P l Name Y B R Line l or Plane R or Plane ABC A line is a straight path that has no thickness and extends forever. A plane is a flat surface that has no thickness and extends forever.

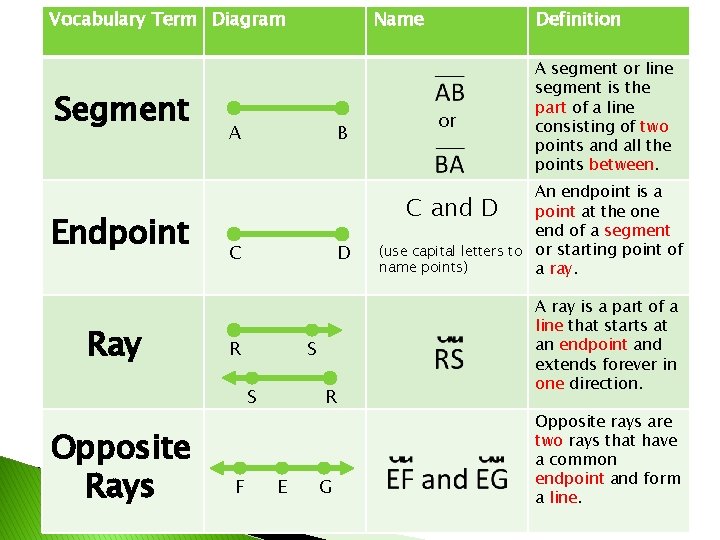
Vocabulary Term Diagram Segment Endpoint Ray A B C D R S S Opposite Rays Name F R E G Definition or A segment or line segment is the part of a line consisting of two points and all the points between. An endpoint is a C and D point at the one end of a segment (use capital letters to or starting point of name points) a ray. A ray is a part of a line that starts at an endpoint and extends forever in one direction. Opposite rays are two rays that have a common endpoint and form a line.

Basic Terms Points that lie on the same line are collinear. The opposite of collinear is noncollinear. K L M N K, L, and M are collinear. K, L, and N are noncollinear.

Basic Terms Coplanar points and lines lie in the same plane. The opposite of coplanar is noncoplanar. This point is noncoplanar to the plane containing the other 4 points.

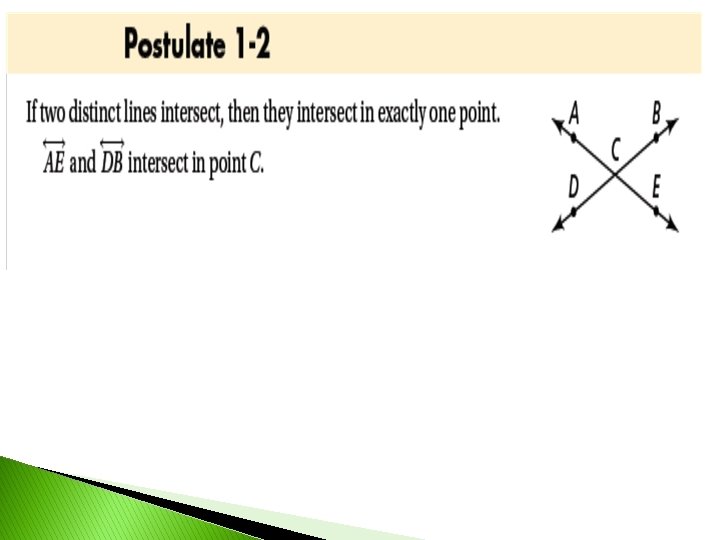
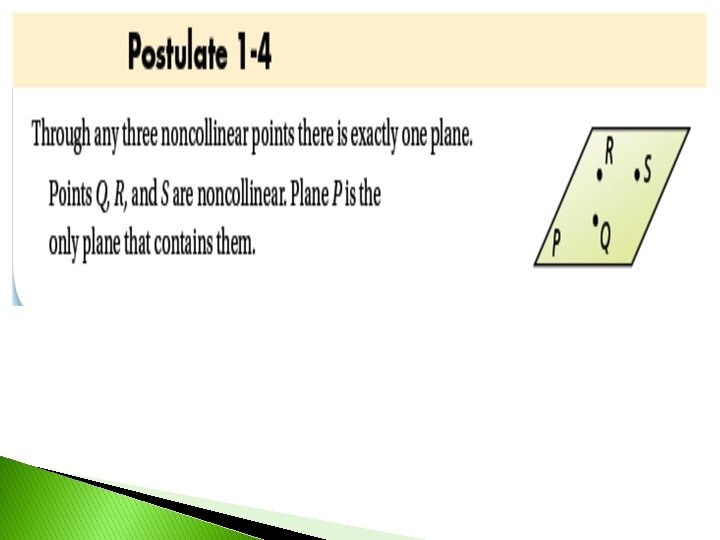
Basic Terms A postulate, or axiom, is an accepted statement of fact without proof. Postulates about points, lines, and planes help describe geometric properties.

Basic Terms �The intersection of two or more geometric figures is the set of points the figures have in common. �Space is the set of all points in three dimensions.

You have one minute! Discuss the following questions with your partners and answer always, sometimes, or never: 1. Two points are __________ collinear. 2. Two lines are _________ coplanar. Answers: 1 is always; 2 is sometimes.

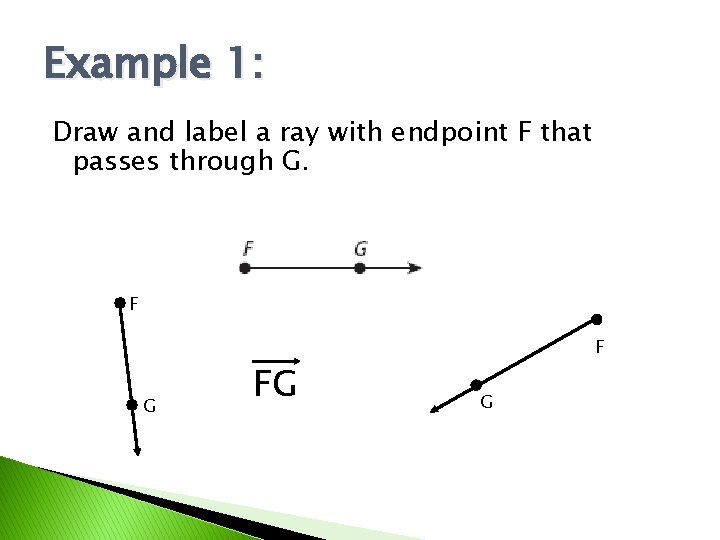
Example 1: Draw and label a ray with endpoint F that passes through G. F G FG F G

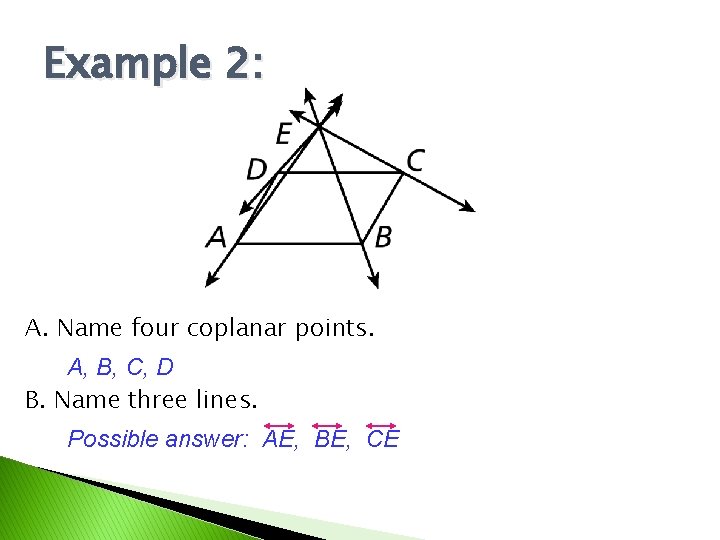
Example 2: A. Name four coplanar points. A, B, C, D B. Name three lines. Possible answer: AE, BE, CE

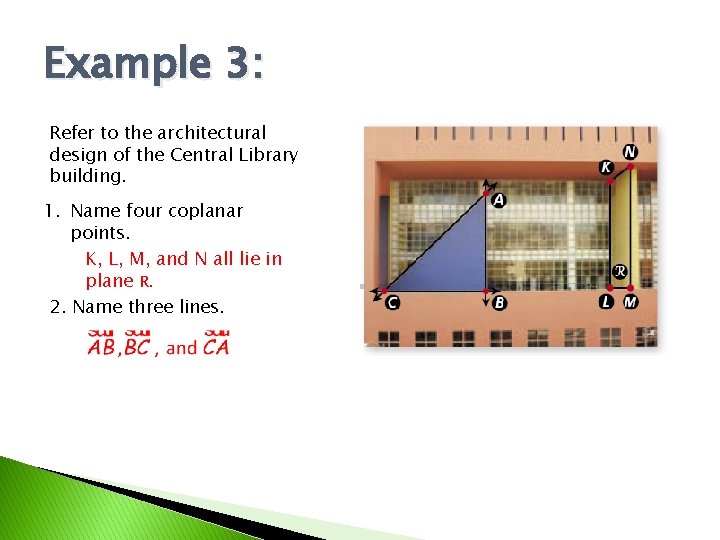
Example 3: Refer to the architectural design of the Central Library building. 1. Name four coplanar points. K, L, M, and N all lie in plane R. 2. Name three lines.

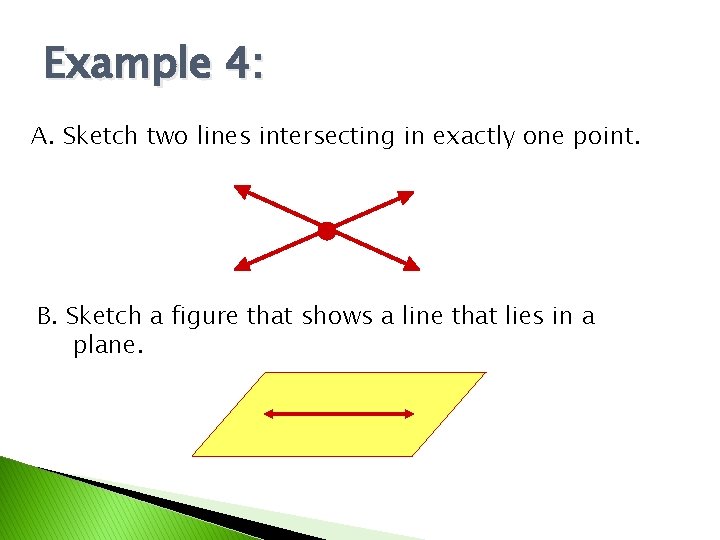
Example 4: A. Sketch two lines intersecting in exactly one point. B. Sketch a figure that shows a line that lies in a plane.

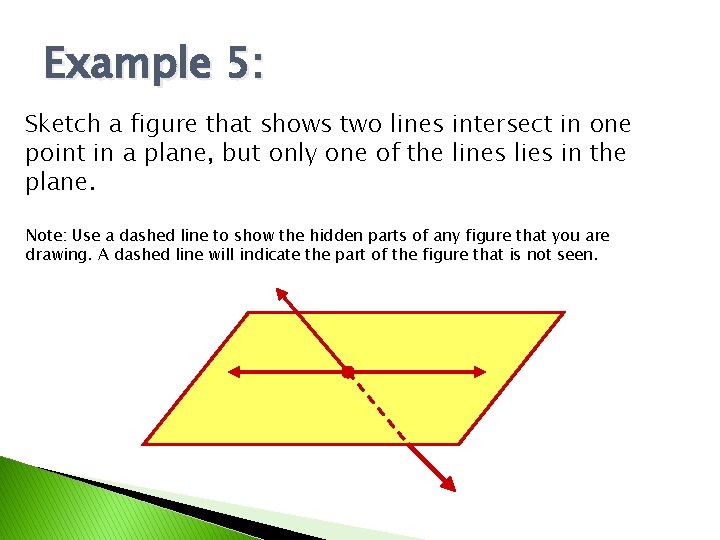
Example 5: Sketch a figure that shows two lines intersect in one point in a plane, but only one of the lines lies in the plane. Note: Use a dashed line to show the hidden parts of any figure that you are drawing. A dashed line will indicate the part of the figure that is not seen.

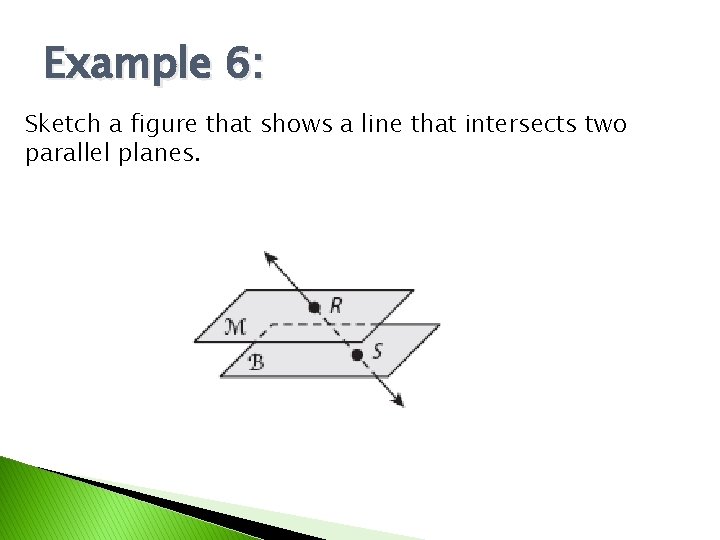
Example 6: Sketch a figure that shows a line that intersects two parallel planes.

Example 7: Sketch a figure that shows three coplanar lines that intersect in three different points.

�FOR EXTRA EXAMPLES NOT USED IN COMPOSITION BOOK FOLLOW, LOG-ON TO YOUR PEARSON ACCOUNT AND GO THROUGH UNIT 1 LESSON 1 -1 BEFORE YOU DO THE ON-LINE HW AND THE WRITTEN HW.