Peak Distortion ISI Analysis Bryan Casper Circuits Research

Peak Distortion ISI Analysis Bryan Casper Circuits Research Lab Intel® Corporation

Agenda • • • Properties of a Linear Time-invariant System (LTI) Margin calculation method (voltage and timing) Worst-case eye opening calculation methods Worst-case eye with crosstalk Complete Peak Distortion equations Compare worst-case eye w/ random data eye, lone 1 or 0 eye, sine wave eye Peak Distortion Analysis Bryan Casper - CRL

Properties of a Linear Timeinvariant System • Impulse response • Convolution • Superposition FFT Frequency response Peak Distortion Analysis Bryan Casper - CRL
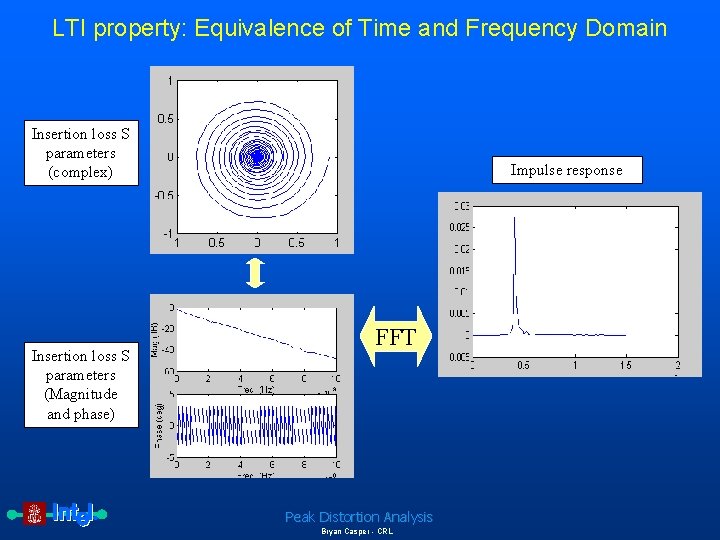
LTI property: Equivalence of Time and Frequency Domain Insertion loss S parameters (complex) Insertion loss S parameters (Magnitude and phase) Impulse response FFT Peak Distortion Analysis Bryan Casper - CRL
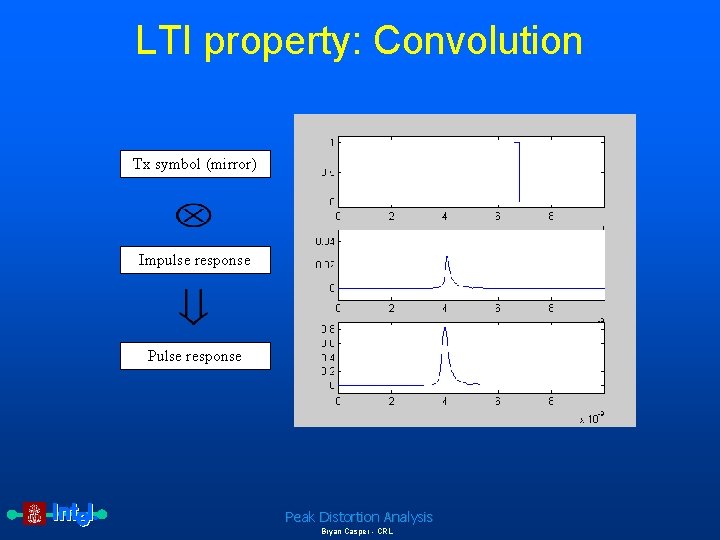
LTI property: Convolution Tx symbol (mirror) Impulse response Peak Distortion Analysis Bryan Casper - CRL

LTI property: Superposition Out In Tx symbol Pulse response … 000010000000… Peak Distortion Analysis Bryan Casper - CRL
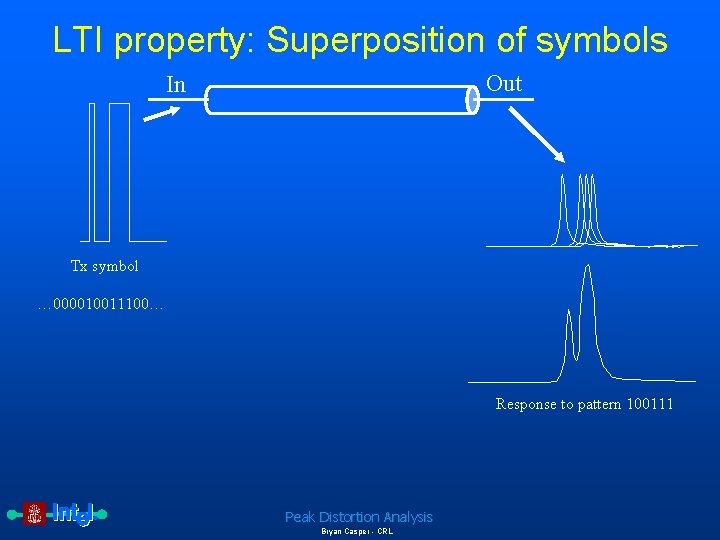
LTI property: Superposition of symbols Out In Tx symbol … 000010011100… Response to pattern 100111 Peak Distortion Analysis Bryan Casper - CRL
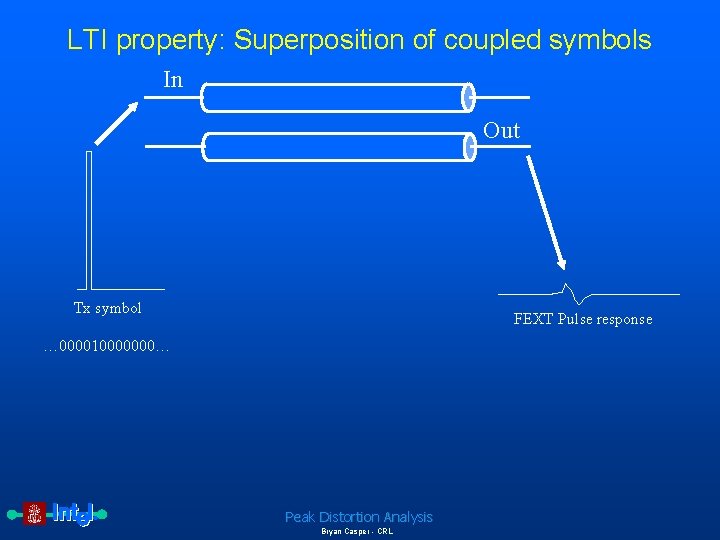
LTI property: Superposition of coupled symbols In Out Tx symbol FEXT Pulse response … 000010000000… Peak Distortion Analysis Bryan Casper - CRL
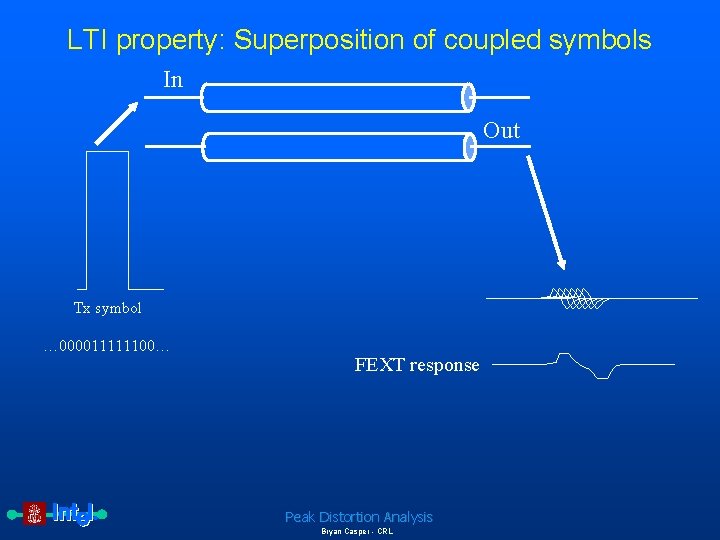
LTI property: Superposition of coupled symbols In Out Tx symbol … 000011111100… FEXT response Peak Distortion Analysis Bryan Casper - CRL
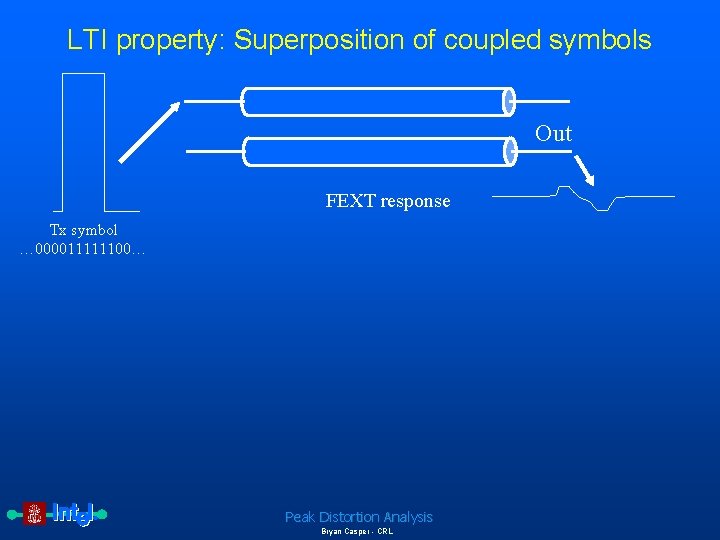
LTI property: Superposition of coupled symbols Out FEXT response Tx symbol … 000011111100… Peak Distortion Analysis Bryan Casper - CRL
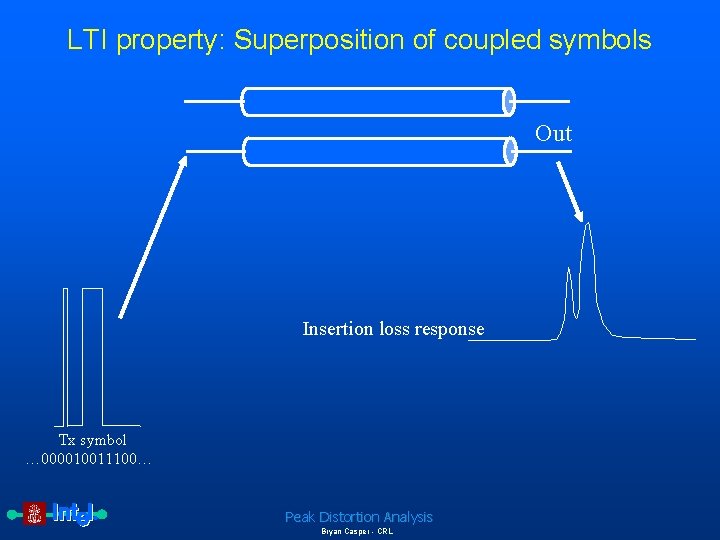
LTI property: Superposition of coupled symbols Out Insertion loss response Tx symbol … 000010011100… Peak Distortion Analysis Bryan Casper - CRL
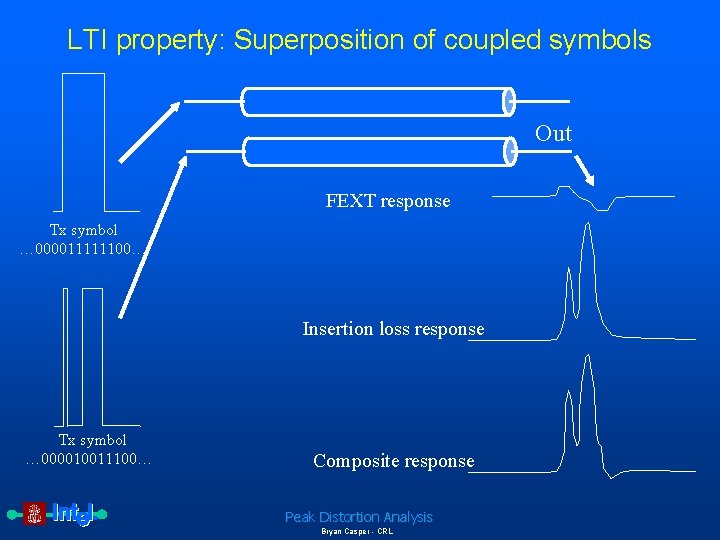
LTI property: Superposition of coupled symbols Out FEXT response Tx symbol … 000011111100… Insertion loss response Tx symbol … 000010011100… Composite response Peak Distortion Analysis Bryan Casper - CRL

Max data rate calculation method • Determine maximum value of all sample timing uncertainty (not including ISI) – Transmitter and receiver sampling jitter – Clock vs. Data skew • Determine maximum value of all voltage uncertainty (not including ISI) – – – Power supply noise*PSRR Common mode noise*CMRR Thermal noise Comparator sensitivity Comparator offset • Determine worst-case eye Peak Distortion Analysis Bryan Casper - CRL
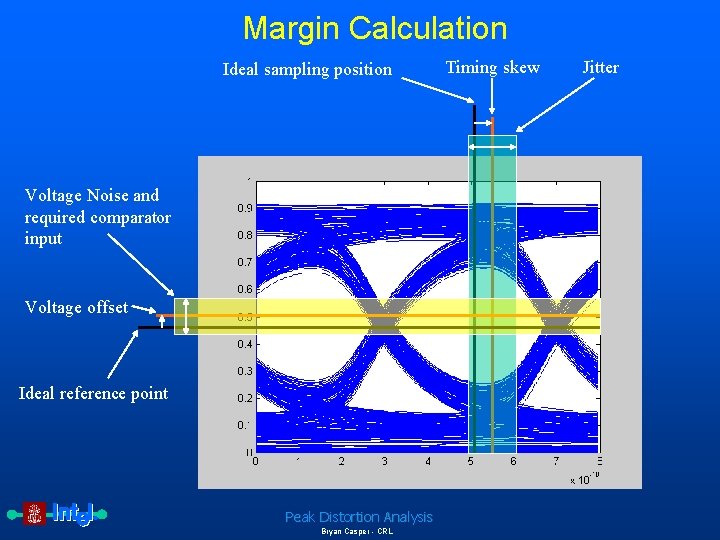
Margin Calculation Ideal sampling position Voltage Noise and required comparator input Voltage offset Ideal reference point Peak Distortion Analysis Bryan Casper - CRL Timing skew Jitter
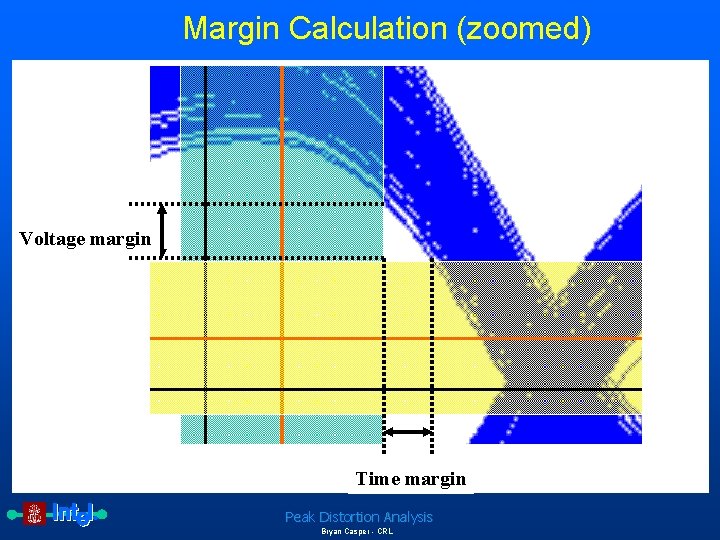
Margin Calculation (zoomed) Ideal sampling position Timing skew Voltage Noise and required comparator input Voltage margin Voltage offset Ideal sampling position Time margin Peak Distortion Analysis Bryan Casper - CRL Jitter

Worst-case eye calculation • Eye diagrams are generally calculated empirically – Convolve random data with pulse response of channel – Pulse response is derived by convolving the impulse reponse with the transmitted symbol • For eye diagrams to represent the worst-case, a large set of random data must be used – Low probability of hitting worst case data transitions – Computationally inefficient • An analytical method of producing the worst-case eye diagram exists – Computationally efficient algorithm Peak Distortion Analysis Bryan Casper - CRL

Peak Distortion Analysis Reference • Peak distortion analysis of ISI has been used for many years – J. G. Proakis, Digital Communications, 3 rd ed. , Singapore: Mc. Graw-Hill, 1995, pp. 602 -603 (not much detailed info here) Peak Distortion Analysis Bryan Casper - CRL

Interconnect Model • • • Point to point differential desktop topology Differential, edge-coupled microstrip (10” @ 55Ω) 2 Sockets 2 Packages (2” @ 45Ω) 1 p. F pad capacitance 50Ω single-ended termination pkg socket 10” μstrip Peak Distortion Analysis Bryan Casper - CRL socket pkg
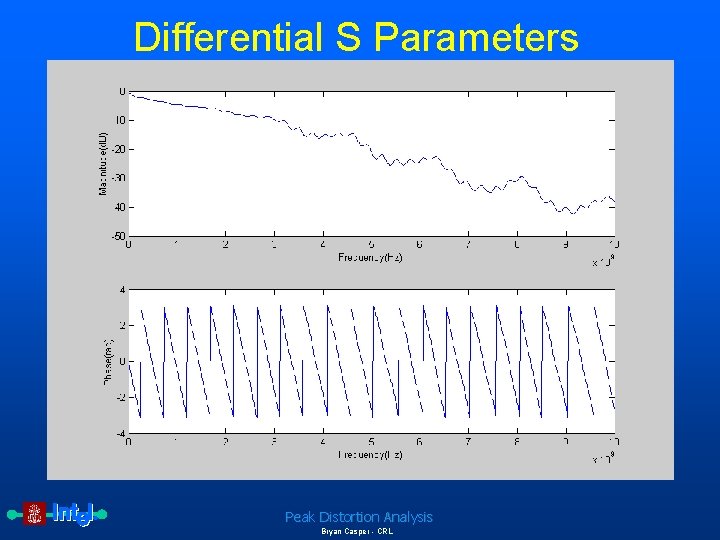
Differential S Parameters Peak Distortion Analysis Bryan Casper - CRL
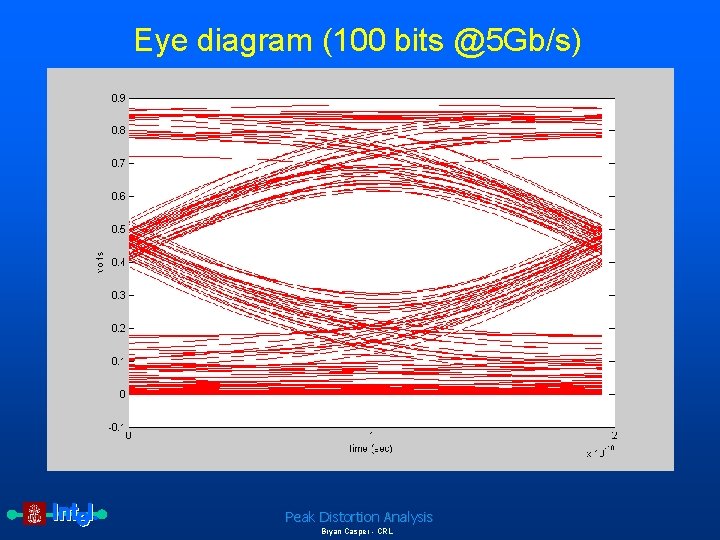
Eye diagram (100 bits @5 Gb/s) Peak Distortion Analysis Bryan Casper - CRL
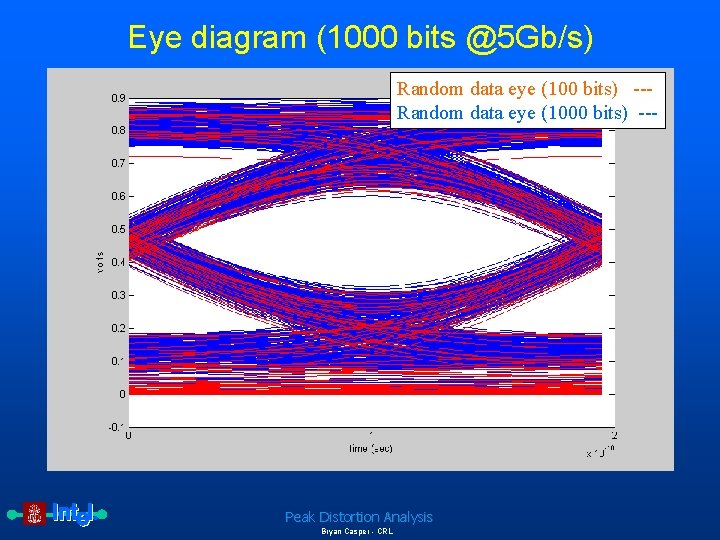
Eye diagram (1000 bits @5 Gb/s) Random data eye (100 bits) --Random data eye (1000 bits) --- Peak Distortion Analysis Bryan Casper - CRL
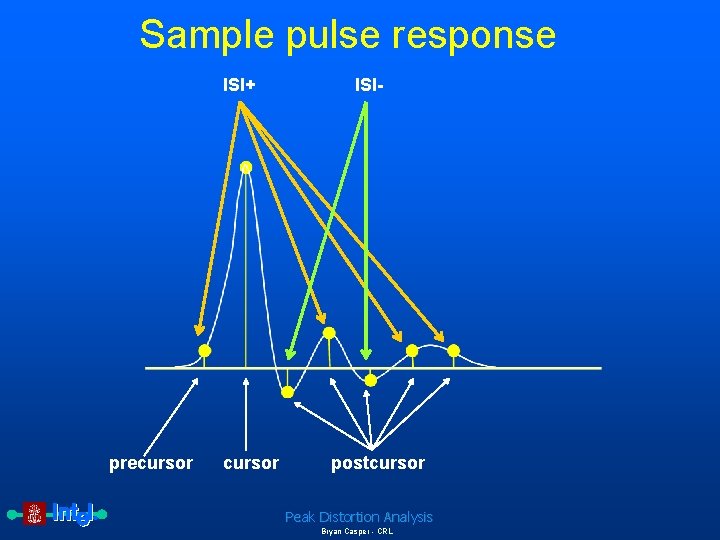
Sample pulse response ISI+ precursor ISI- postcursor Peak Distortion Analysis Bryan Casper - CRL
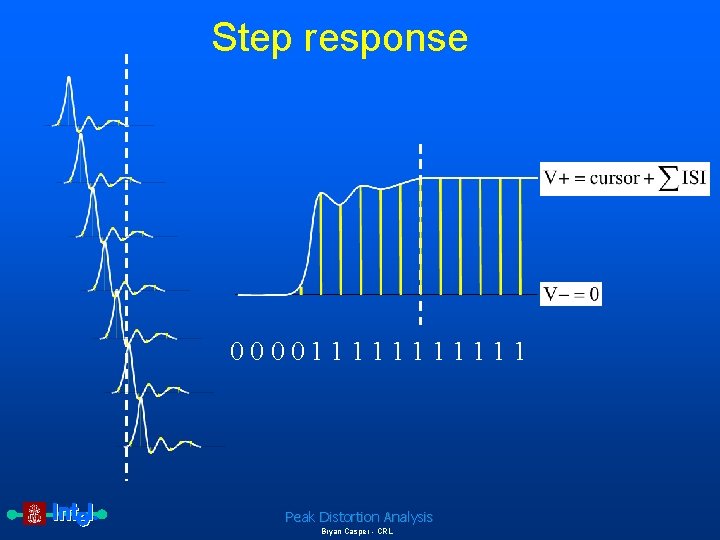
Step response 0000111111 Peak Distortion Analysis Bryan Casper - CRL
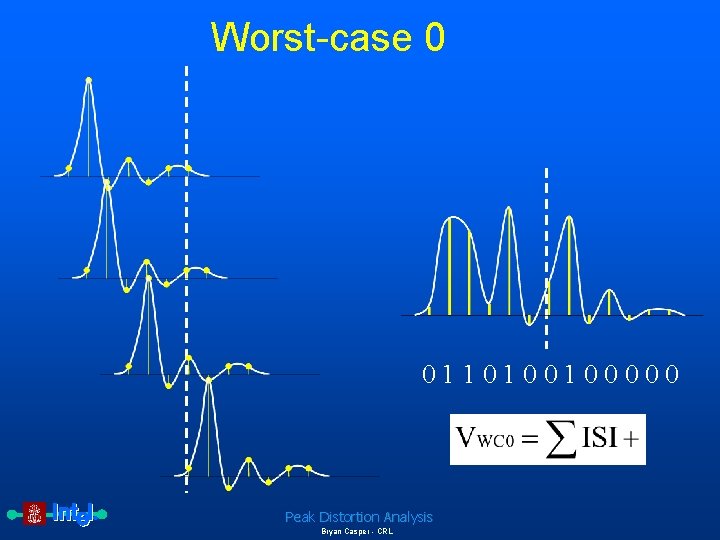
Worst-case 0 0110100100000 Peak Distortion Analysis Bryan Casper - CRL
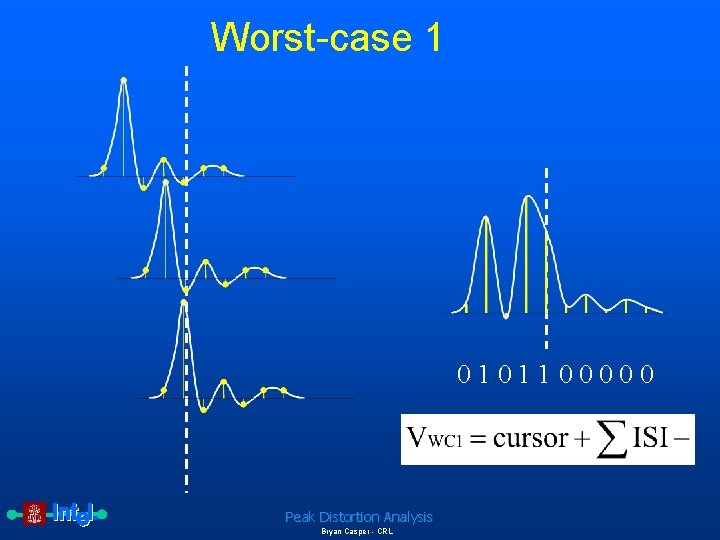
Worst-case 1 0101100000 Peak Distortion Analysis Bryan Casper - CRL
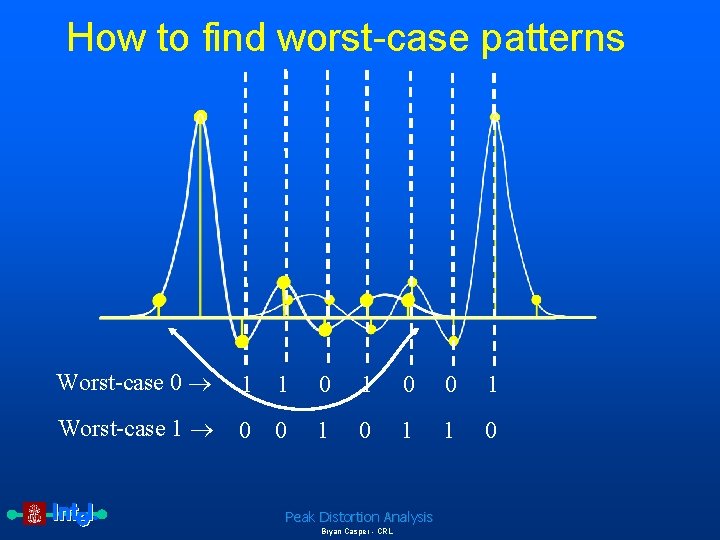
How to find worst-case patterns Worst-case 0 1 1 0 0 1 Worst-case 1 0 0 1 1 0 Peak Distortion Analysis Bryan Casper - CRL

Ideal reference placement 0110100100000 0101100000 Peak Distortion Analysis Bryan Casper - CRL
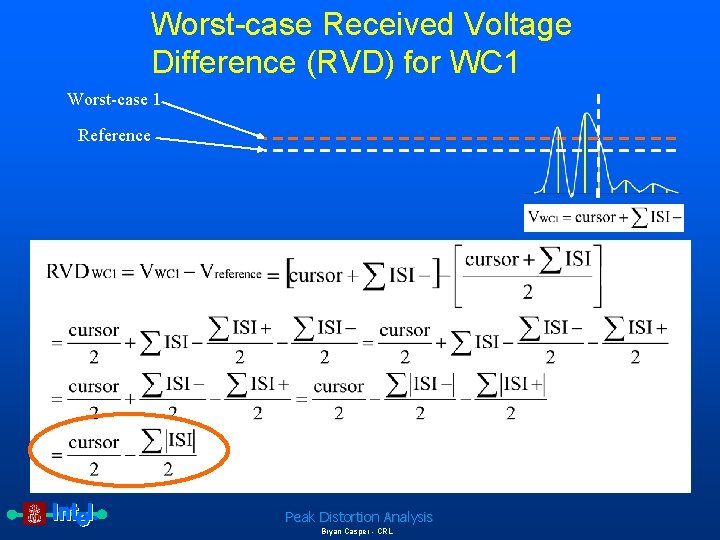
Worst-case Received Voltage Difference (RVD) for WC 1 Worst-case 1 Reference Peak Distortion Analysis Bryan Casper - CRL

Worst-case Received Voltage Difference (RVD) for WC 0 Reference Worst-case 0 Peak Distortion Analysis Bryan Casper - CRL
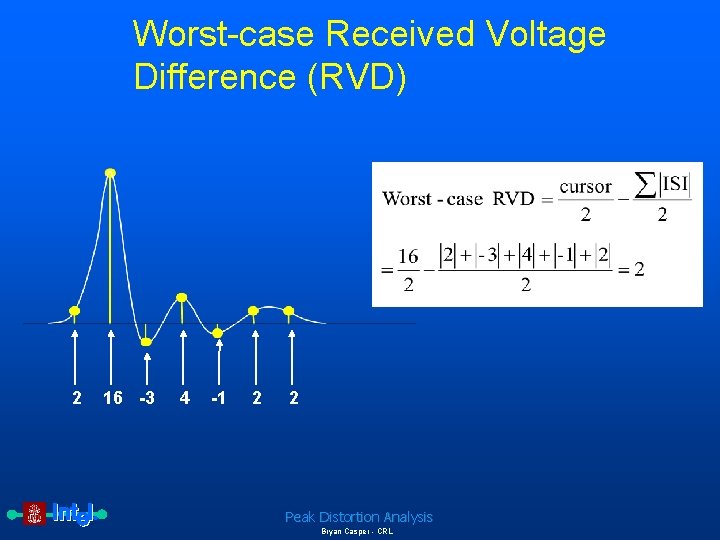
Worst-case Received Voltage Difference (RVD) 2 16 -3 4 -1 2 2 Peak Distortion Analysis Bryan Casper - CRL
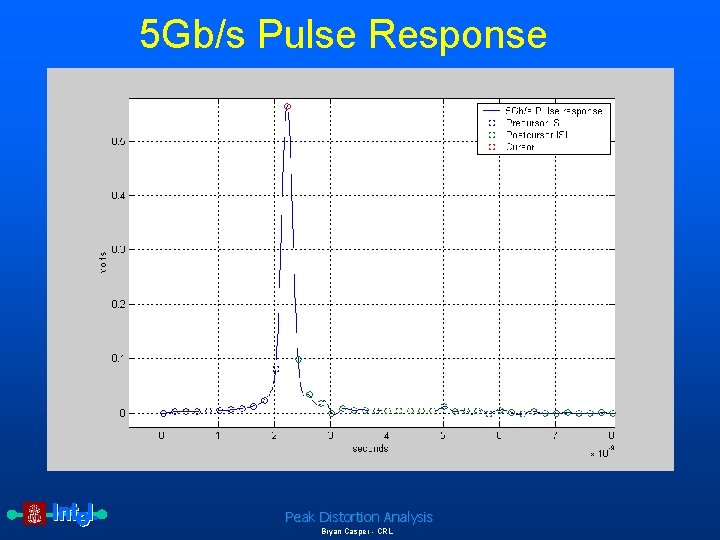
5 Gb/s Pulse Response Peak Distortion Analysis Bryan Casper - CRL
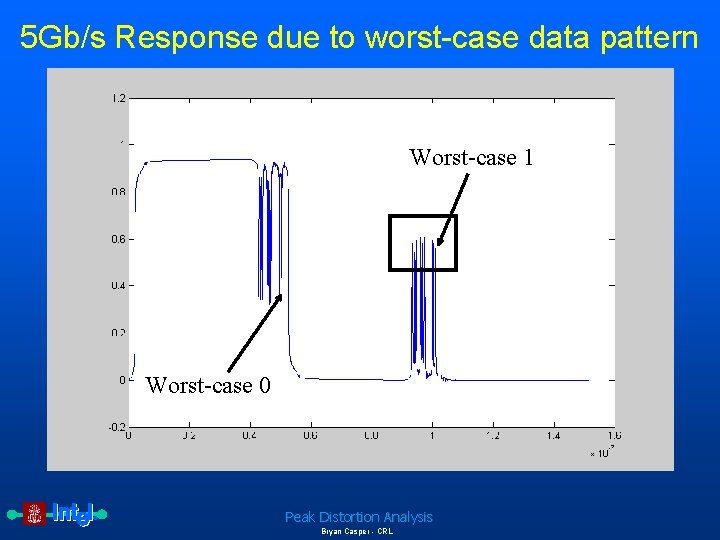
5 Gb/s Response due to worst-case data pattern Worst-case 1 Worst-case 0 Peak Distortion Analysis Bryan Casper - CRL
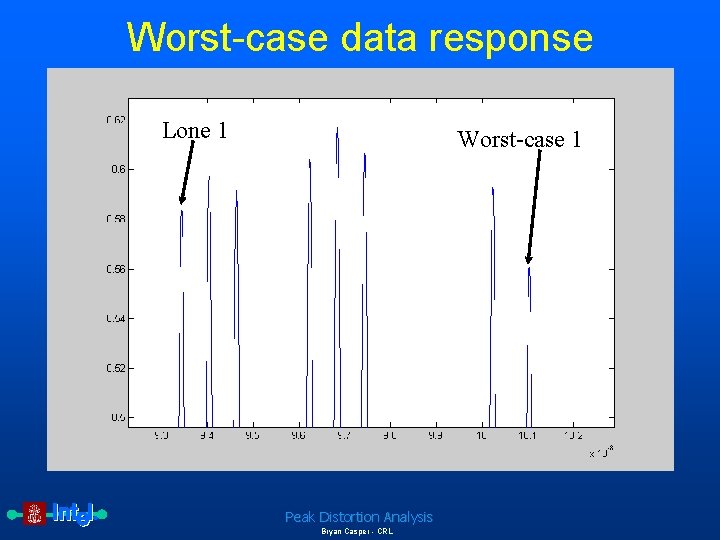
Worst-case data response Lone 1 Worst-case 1 Peak Distortion Analysis Bryan Casper - CRL
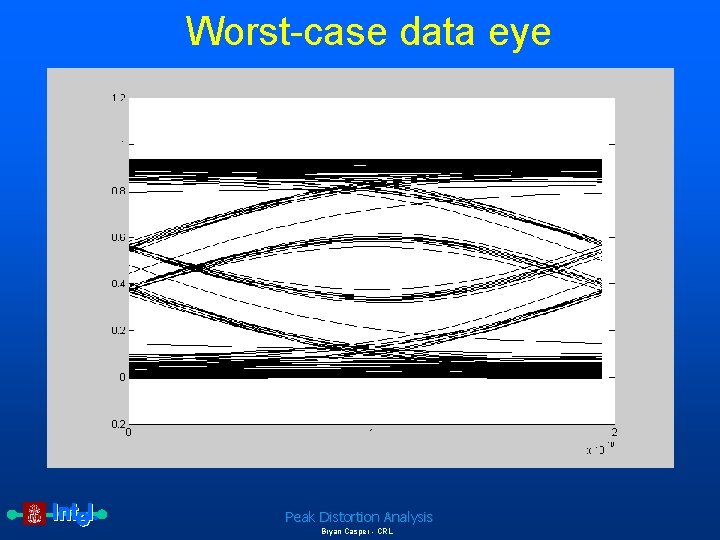
Worst-case data eye Peak Distortion Analysis Bryan Casper - CRL
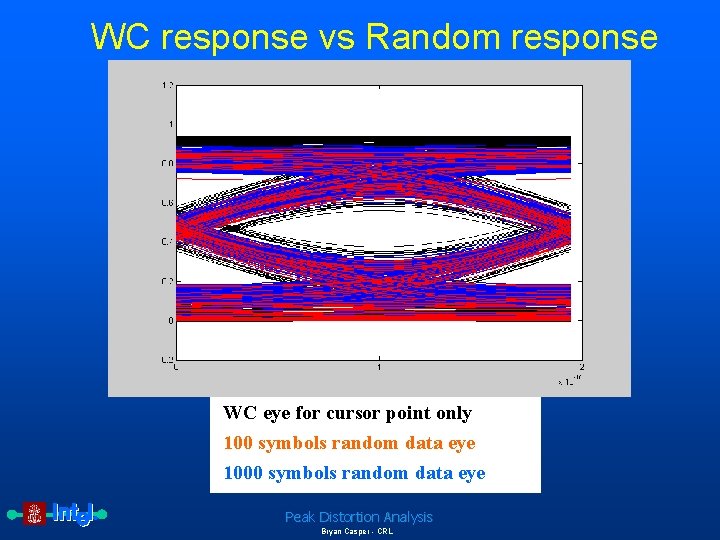
WC response vs Random response WC eye for cursor point only 100 symbols random data eye 1000 symbols random data eye Peak Distortion Analysis Bryan Casper - CRL
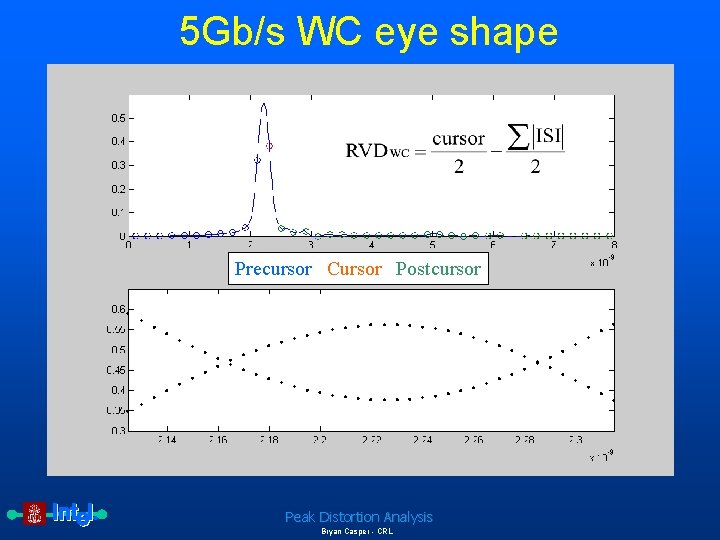
5 Gb/s WC eye shape Precursor Cursor Postcursor Peak Distortion Analysis Bryan Casper - CRL
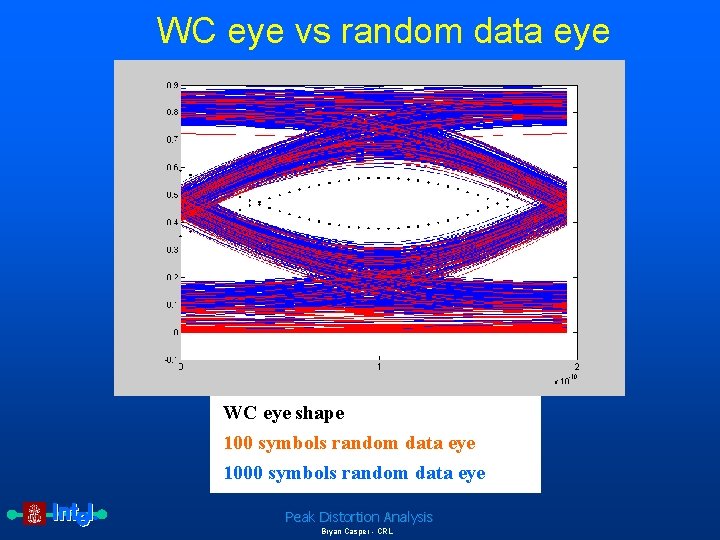
WC eye vs random data eye WC eye shape 100 symbols random data eye 1000 symbols random data eye Peak Distortion Analysis Bryan Casper - CRL
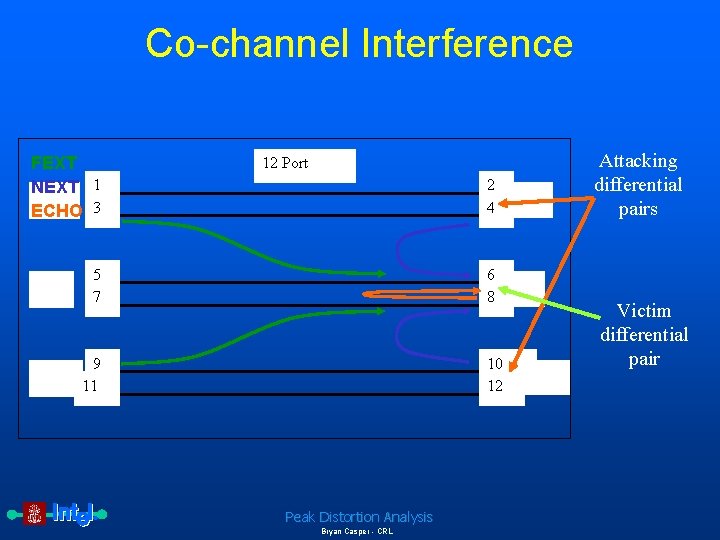
Co-channel Interference FEXT NEXT 1 ECHO 3 12 Port 2 4 5 7 6 8 9 11 10 12 Peak Distortion Analysis Bryan Casper - CRL Attacking differential pairs Victim differential pair
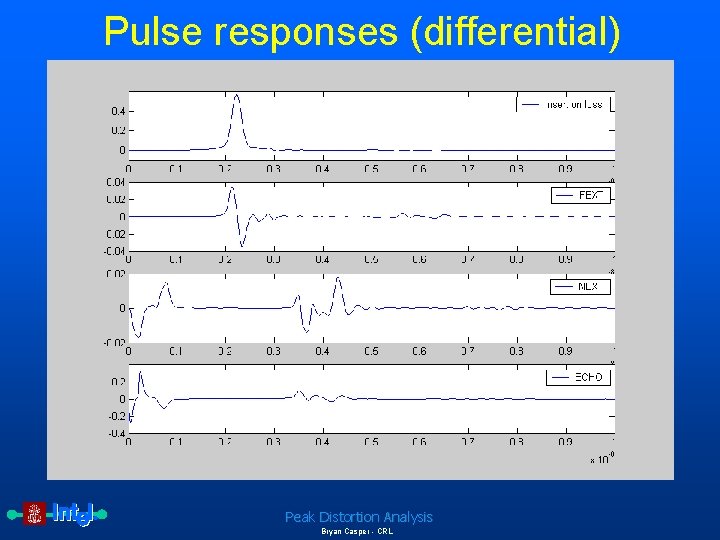
Pulse responses (differential) Peak Distortion Analysis Bryan Casper - CRL
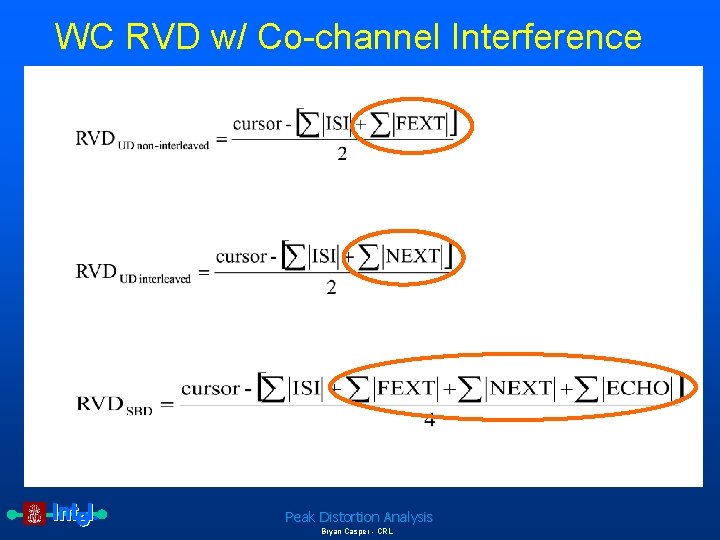
WC RVD w/ Co-channel Interference Peak Distortion Analysis Bryan Casper - CRL
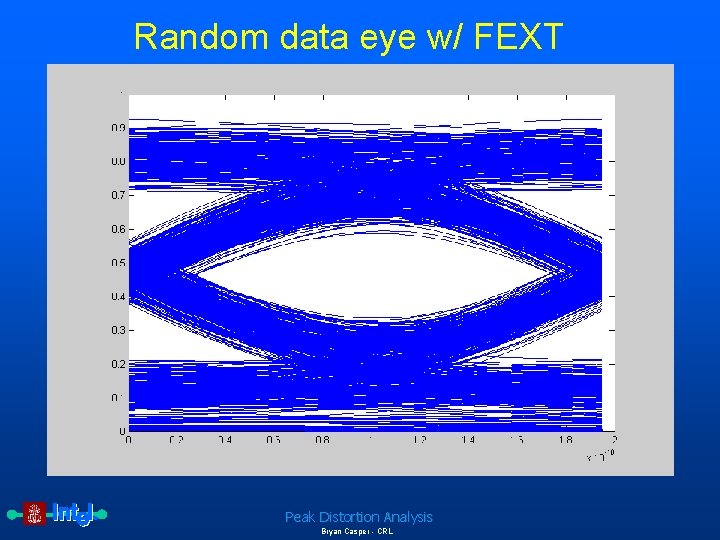
Random data eye w/ FEXT Peak Distortion Analysis Bryan Casper - CRL
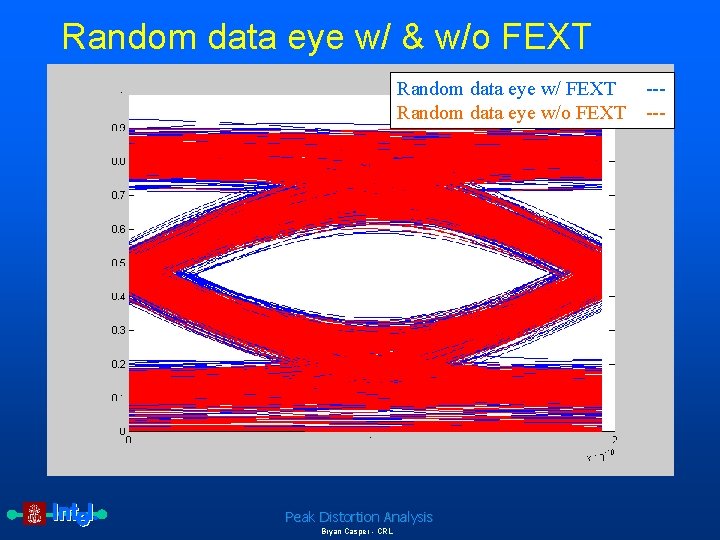
Random data eye w/ & w/o FEXT Random data eye w/o FEXT Peak Distortion Analysis Bryan Casper - CRL -----

WC eye w/ & w/o FEXT Random data eye --WC eye w/o w FEXT … WC eye w FEXT … Peak Distortion Analysis Bryan Casper - CRL

Complete Peak Distortion Equations Peak Distortion Analysis Bryan Casper - CRL

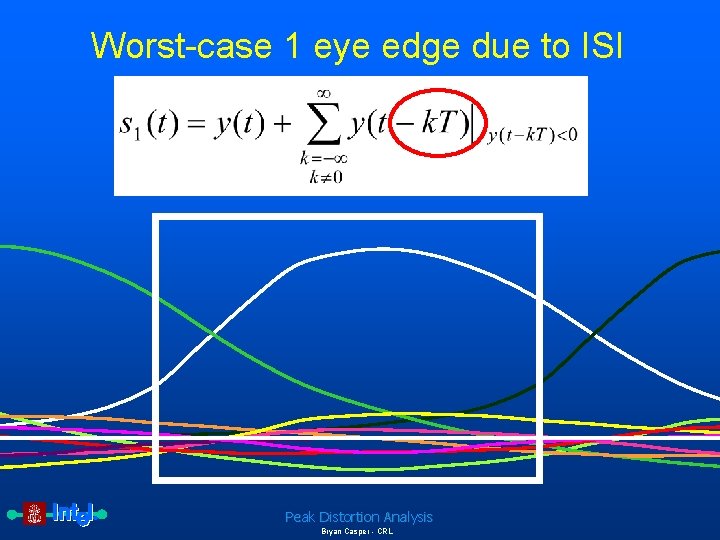
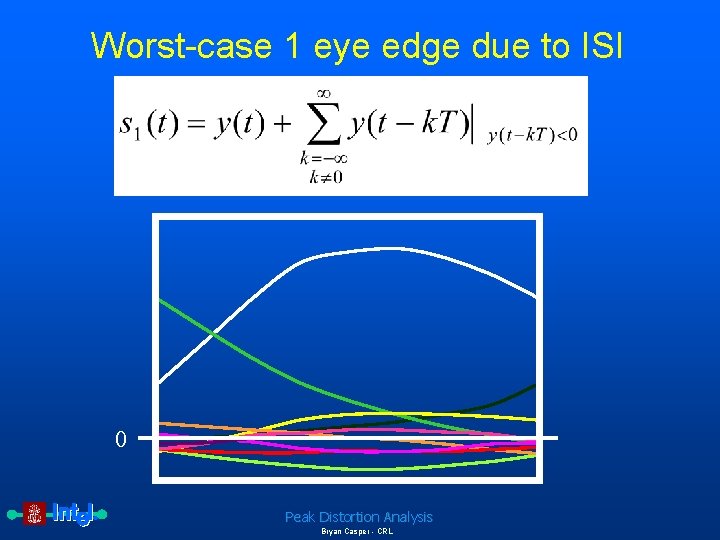
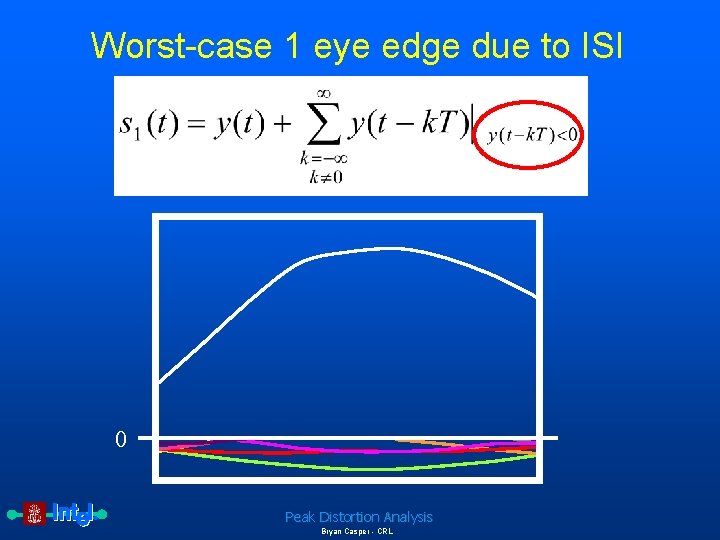
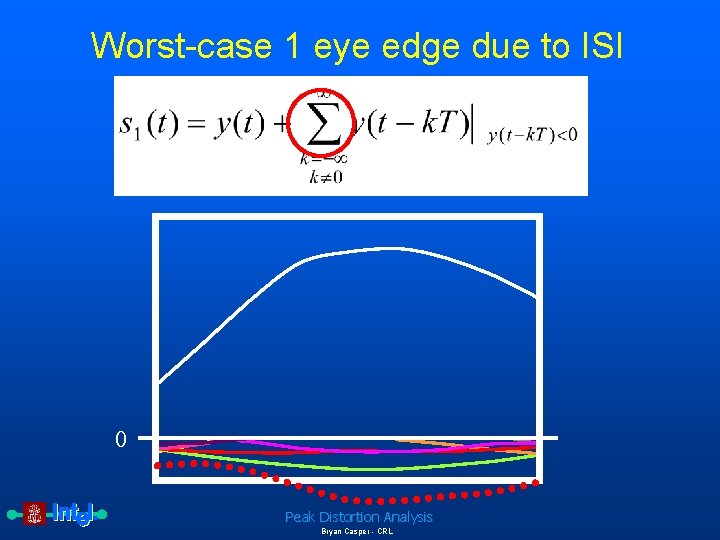
Worst-case 1 eye edge due to ISI • Definitions – y(t) is the pulse response of the interconnect – T is the symbol period – s 1 is the eye edge due to a worst case 1 Peak Distortion Analysis Bryan Casper - CRL
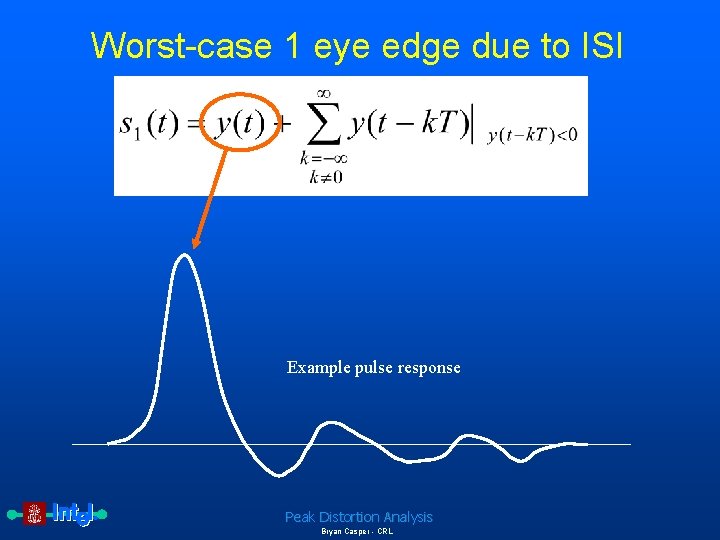
Worst-case 1 eye edge due to ISI Example pulse response Peak Distortion Analysis Bryan Casper - CRL
Worst-case 1 eye edge due to ISI Peak Distortion Analysis Bryan Casper - CRL
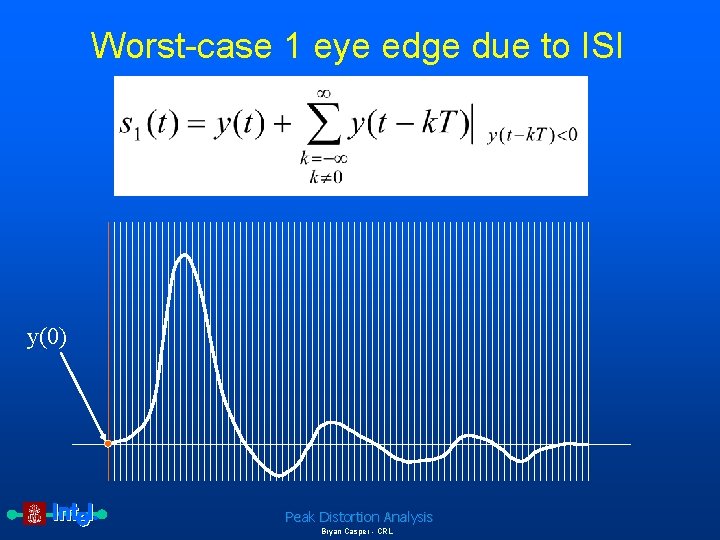
Worst-case 1 eye edge due to ISI y(0) Peak Distortion Analysis Bryan Casper - CRL
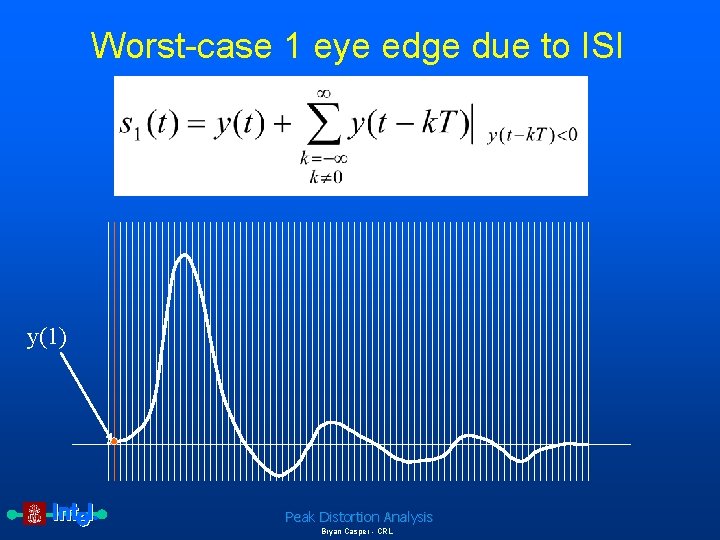
Worst-case 1 eye edge due to ISI y(1) Peak Distortion Analysis Bryan Casper - CRL
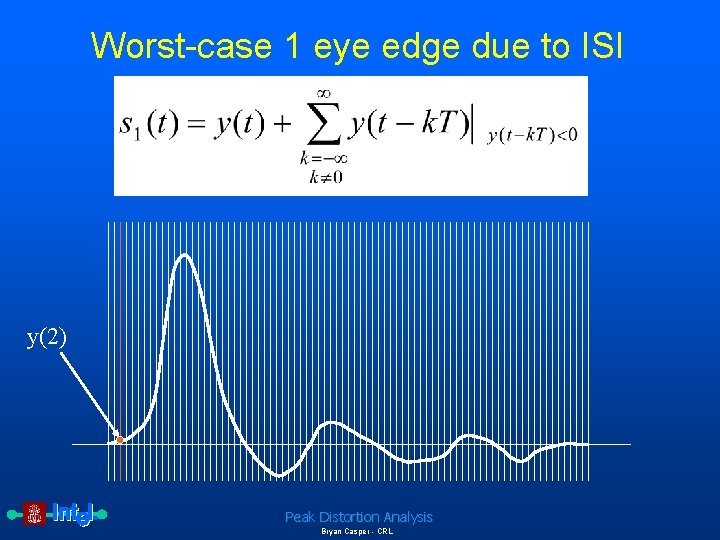
Worst-case 1 eye edge due to ISI y(2) Peak Distortion Analysis Bryan Casper - CRL
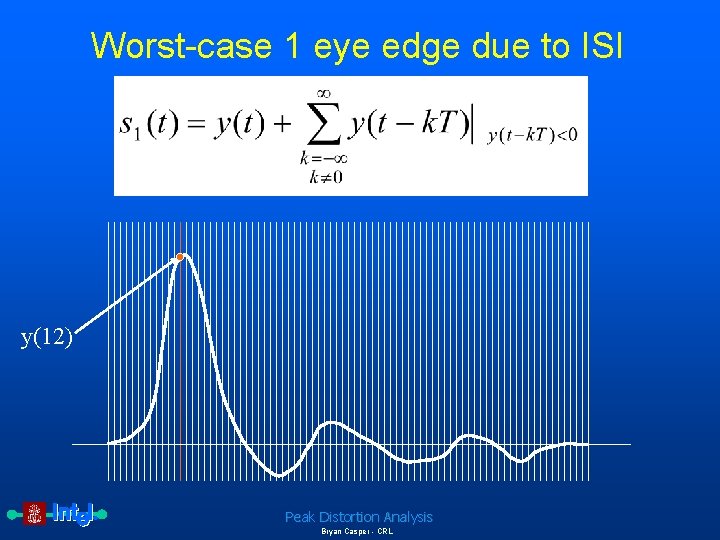
Worst-case 1 eye edge due to ISI y(12) Peak Distortion Analysis Bryan Casper - CRL
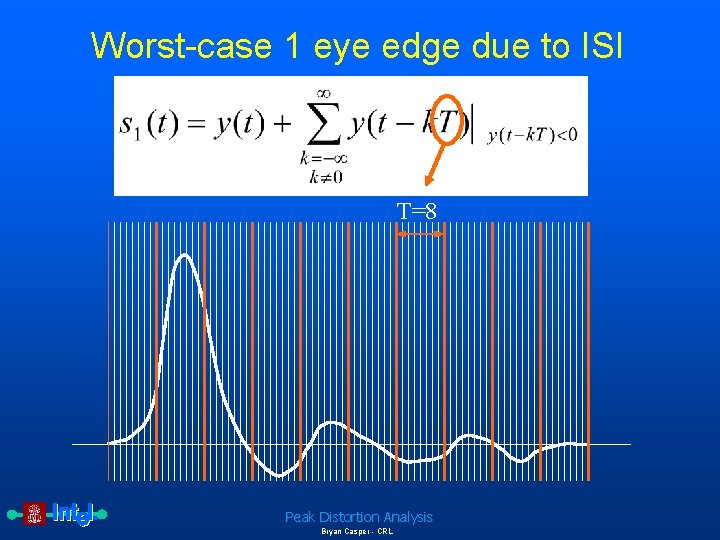
Worst-case 1 eye edge due to ISI T=8 Peak Distortion Analysis Bryan Casper - CRL
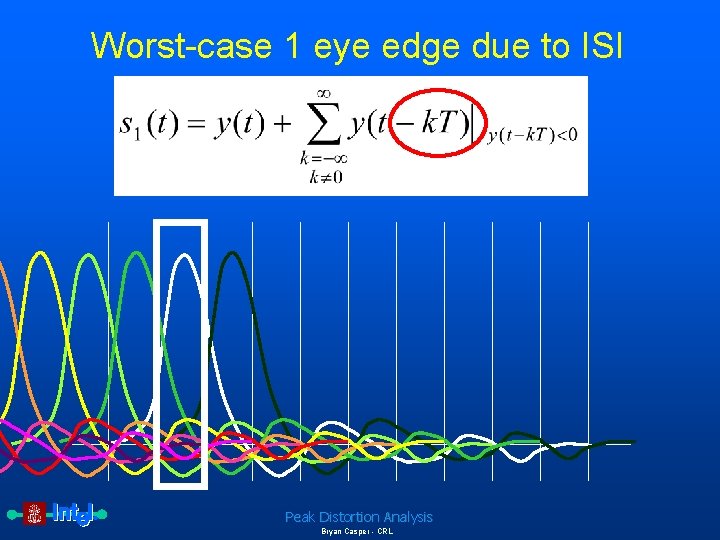
Worst-case 1 eye edge due to ISI Peak Distortion Analysis Bryan Casper - CRL
Worst-case 1 eye edge due to ISI Peak Distortion Analysis Bryan Casper - CRL
Worst-case 1 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
Worst-case 1 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
Worst-case 1 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
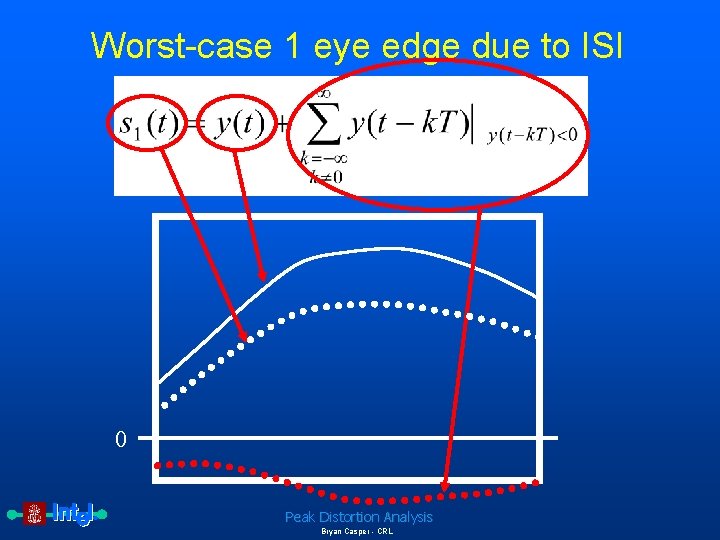
Worst-case 1 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
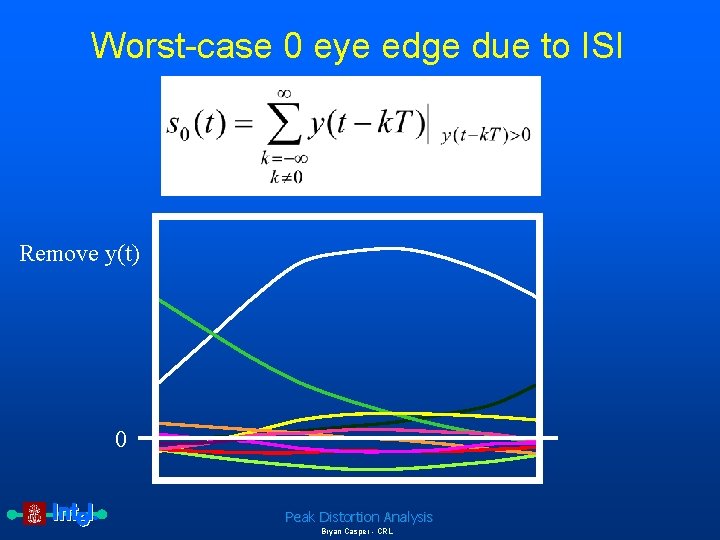
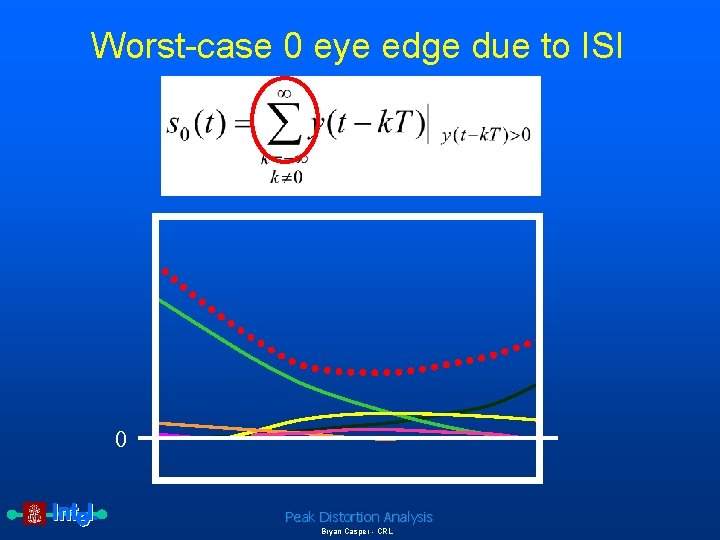
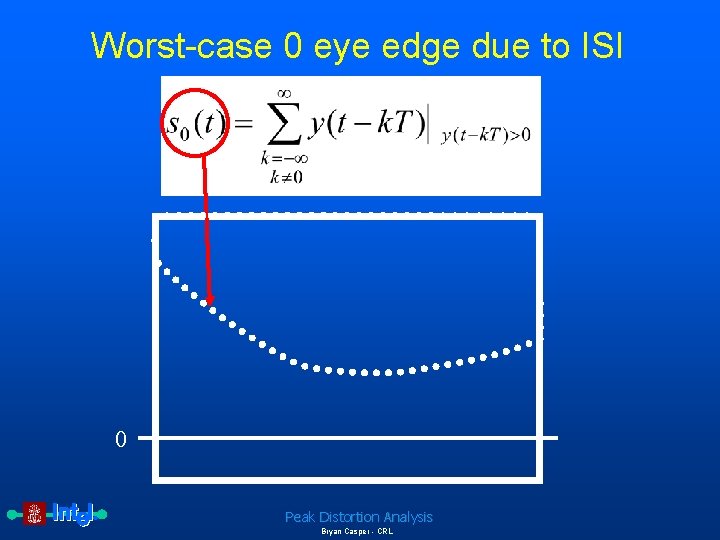
Worst-case 0 eye edge due to ISI Remove y(t) 0 Peak Distortion Analysis Bryan Casper - CRL
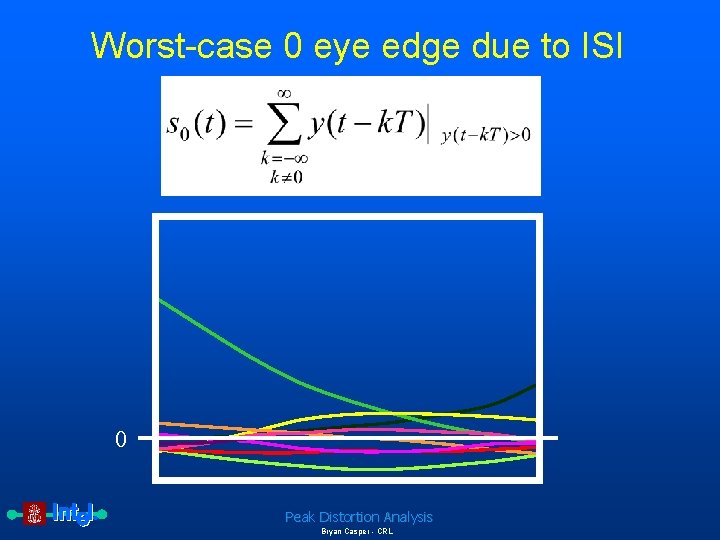
Worst-case 0 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
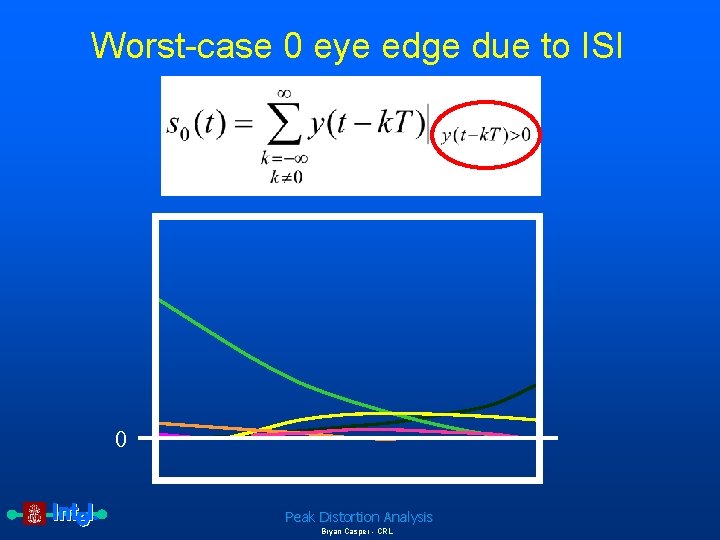
Worst-case 0 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
Worst-case 0 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
Worst-case 0 eye edge due to ISI 0 Peak Distortion Analysis Bryan Casper - CRL
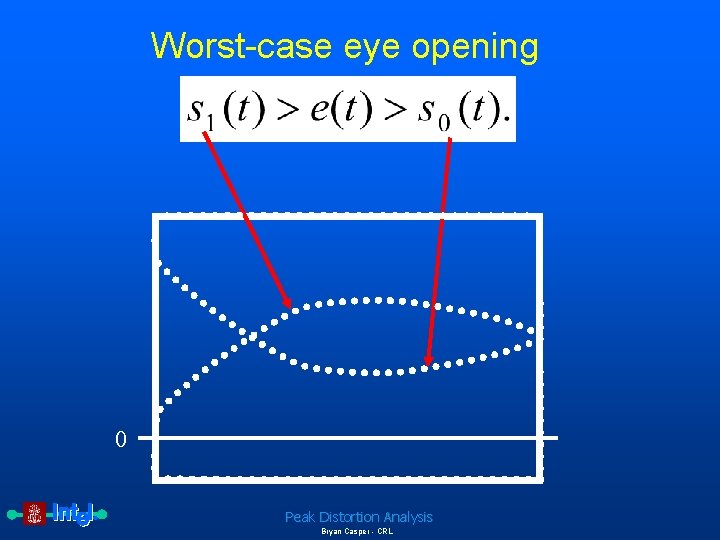
Worst-case eye opening 0 Peak Distortion Analysis Bryan Casper - CRL
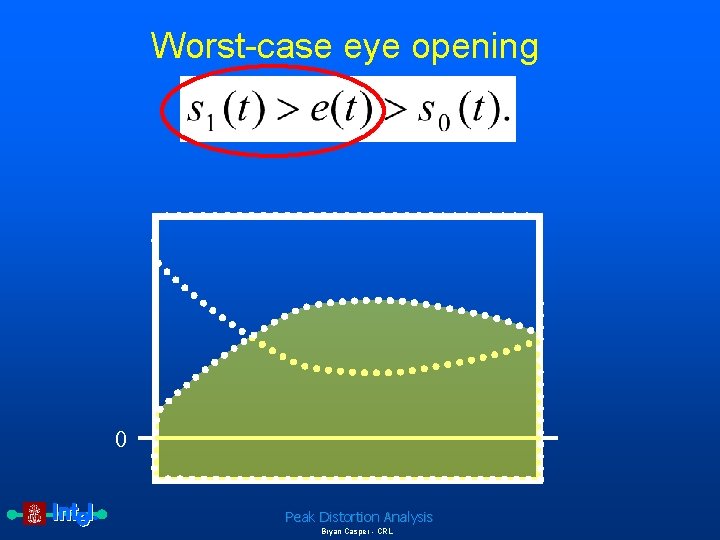
Worst-case eye opening 0 Peak Distortion Analysis Bryan Casper - CRL
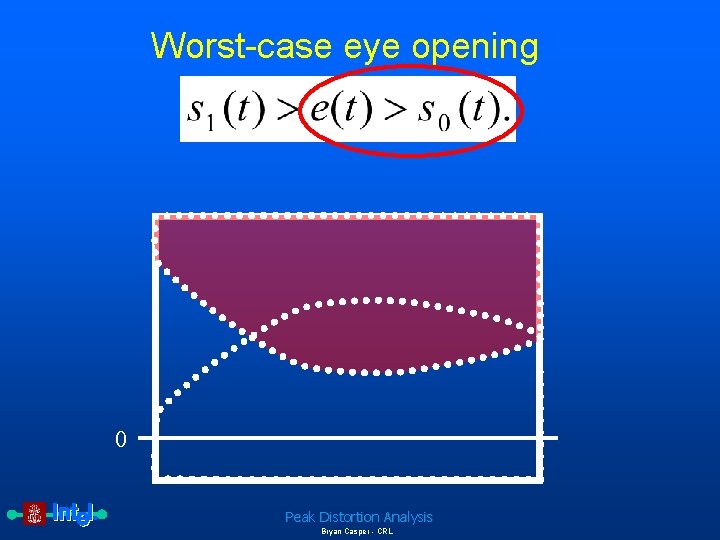
Worst-case eye opening 0 Peak Distortion Analysis Bryan Casper - CRL
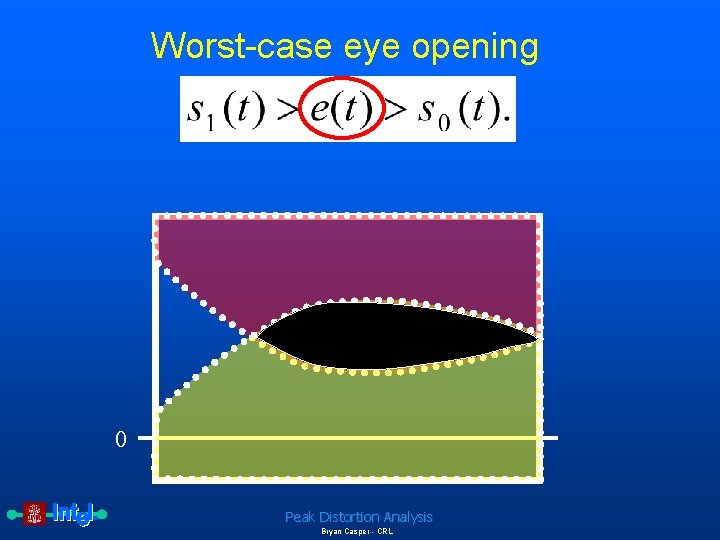
Worst-case eye opening 0 Peak Distortion Analysis Bryan Casper - CRL

Worst-case eye edges with ISI and CCI Worst-case 1 eye edge where ti is the relative sampling point of each cochannel pulse response. Worst-case 0 eye edge Peak Distortion Analysis Bryan Casper - CRL

How do different methods of SI analysis compare with peak distortion analysis? • Random data eye • Lone pulse method • Frequency domain method – Measure the output amplitude due to a sine wave input (sine wave freq = data rate/2) Peak Distortion Analysis Bryan Casper - CRL
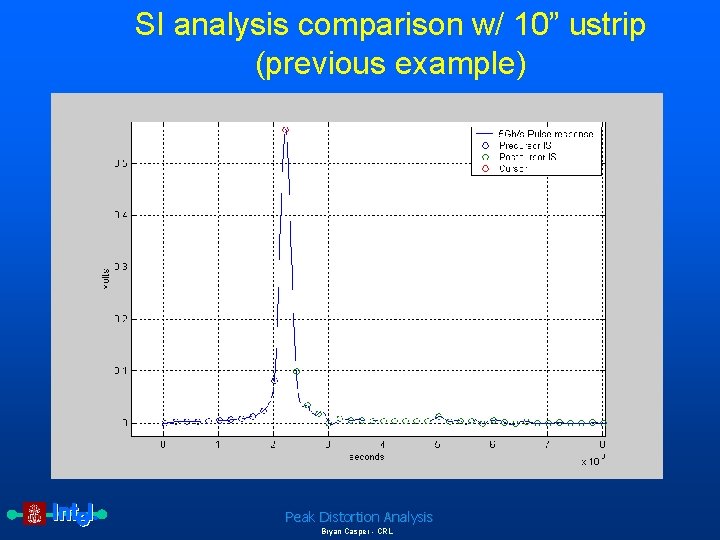
SI analysis comparison w/ 10” ustrip (previous example) Peak Distortion Analysis Bryan Casper - CRL
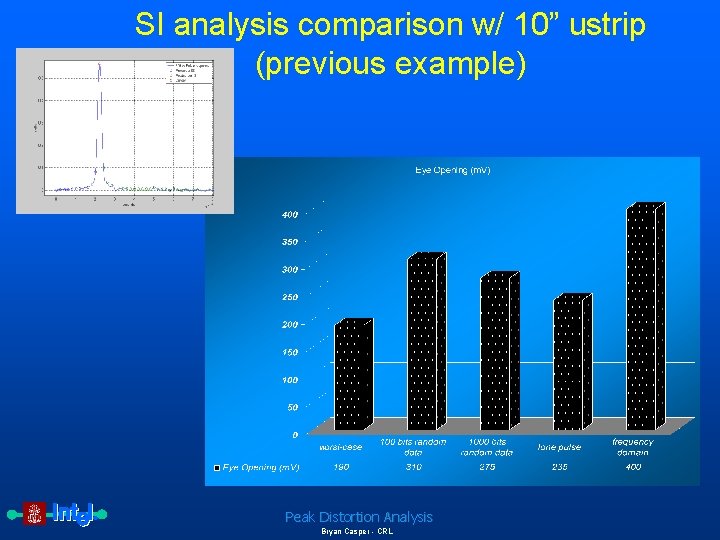
SI analysis comparison w/ 10” ustrip (previous example) Peak Distortion Analysis Bryan Casper - CRL
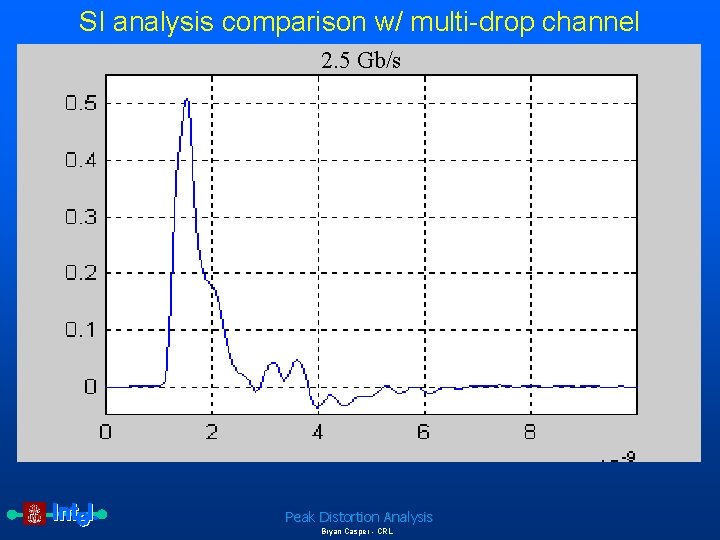
SI analysis comparison w/ multi-drop channel 2. 5 Gb/s Peak Distortion Analysis Bryan Casper - CRL
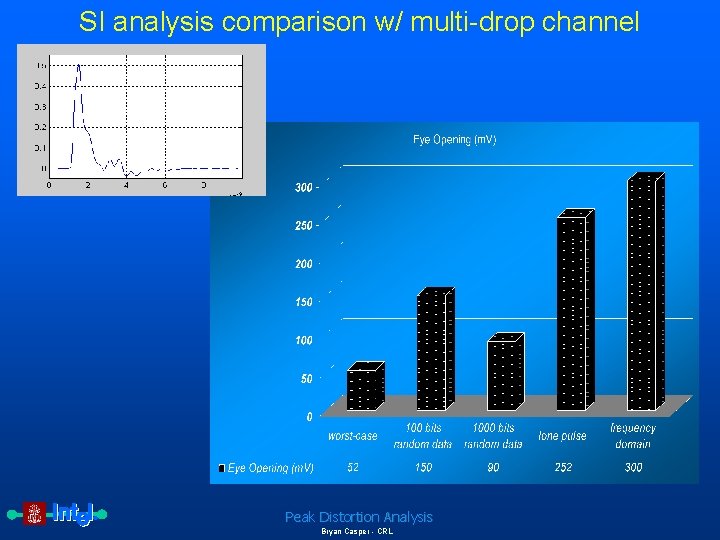
SI analysis comparison w/ multi-drop channel Peak Distortion Analysis Bryan Casper - CRL

Conclusion • Given S Parameters and the corresponding pulse response, the worst case eye shape can be determined analytically • Worst-case co-channel interference can also be determined analytically • Advantages – Objective, Exact, Computationally Efficient Peak Distortion Analysis Bryan Casper - CRL

Backup Peak Distortion Analysis Bryan Casper - CRL

Complete equations for peak distortion analysis To determine the worst-case voltage or timing margin, the worst-case received eye shape is extracted along with the peak sampling boundary. Since sources such as intersymbol and cochannel interference have truncated distributions, the associated worst-case magnitudes can be directly calculated from the unit pulse responses of the system. The unit pulse response y(t) of a system is given by Equation 1: Unit pulse response of a communication system where c(t) is the transmitter symbol response, p(t) is the impulse response of the channel and receiver and denotes convolution. The eye edge due to the worstcase 1 is given by Equation 2: Worst-case 1 eye edge due to ISI where T is the symbol period. Peak Distortion Analysis Bryan Casper - CRL

Complete equations for peak distortion analysis If n cochannel interference sources exist and yi is the cochannel pulse response, the worst-case 1 eye edge becomes Equation 3: Worst-case 1 eye edge due to ISI and cochannel interference where ti is the relative sampling point of each cochannel pulse response. Peak Distortion Analysis Bryan Casper - CRL

Complete equations for peak distortion analysis The eye edge due to the worst-case 0 is given by Equation 4: Worst-case 0 eye edge Therefore, the worst-case eye opening, e(t), is defined as Peak Distortion Analysis Bryan Casper - CRL
- Slides: 78