PDB3 Metode Beda Hingga Finite Difference Method 1

PDB#3 Metode Beda Hingga (Finite Difference Method) 1

Definisi n n Metode beda hingga digunakan untuk menyelesaikan pers. diff biasa dengan syarat batas bukan persamaan diff dengan nilai awal. Disebut sebagai masalah nilai batas. 2

Metode Beda Hingga Contoh dari sebuah nilai batas dari persamaan diferensial biasa : Turunan persamaan diff tsb. disubstitusi oleh pendekatan beda hingga, seperti : 3

Contoh Pengujian ketahanan pada tekanan pembuluh darah yang diuji. Pada pembuluh darah yang tebal dari radius dalam a dan radius luar b, persamaan diff untuk perpindahan titik u dari ketebalan adalah : Tekanan pembuluh darah dimodelkan sebagai : Substitusi pendekatan ini adalah : 4

Solusi Step 1 Pada titik Step 2 Pada titik Step 3 Pada titik 5

Lanjutan solusi Step 4 Pada titik Step 5 Pada titik Step 6 Pada titik 6

Sistem pemecahan dari persamaan : 7

Lanjutan Solusi 8

Lanjutan Solusi Dengan pendekatan : and Hasilnya : 9

Lanjutan Solusi Step 1 Pada titik Step 2 Pada titik Step 3 Pada titik 10

Lanjutan Solusi Step 4 Pada titik Step 5 Pada titik Step 6 Pada titik 11

Pemecahan sistem dari persamaan 12

Lanjutan Solusi 13

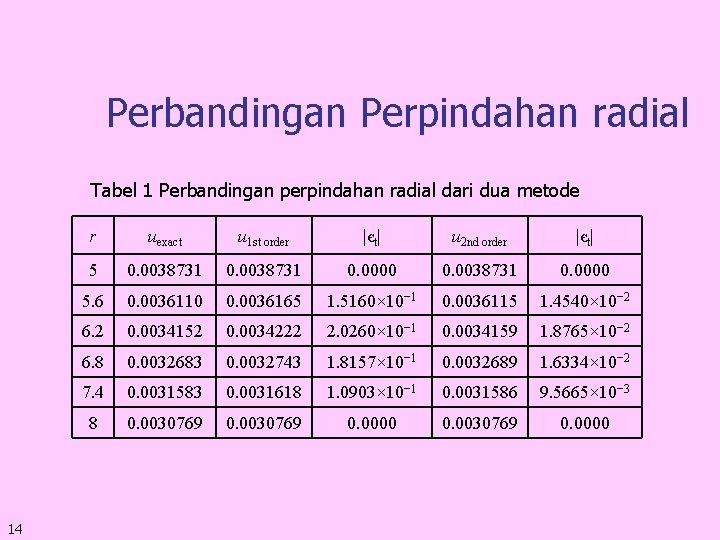
Perbandingan Perpindahan radial Tabel 1 Perbandingan perpindahan radial dari dua metode 14 r uexact u 1 st order |єt| u 2 nd order |єt| 5 0. 0038731 0. 0000 5. 6 0. 0036110 0. 0036165 1. 5160× 10− 1 0. 0036115 1. 4540× 10− 2 6. 2 0. 0034152 0. 0034222 2. 0260× 10− 1 0. 0034159 1. 8765× 10− 2 6. 8 0. 0032683 0. 0032743 1. 8157× 10− 1 0. 0032689 1. 6334× 10− 2 7. 4 0. 0031583 0. 0031618 1. 0903× 10− 1 0. 0031586 9. 5665× 10− 3 8 0. 0030769 0. 0000

SOAL KASUS : Perpindahan radial u dari sebuah silinder berongga tebal bertekanan (jari 2 dalam = 5″, jari 2 luar = 8″) diberikan pada lokasi yang berbeda secara radial. The maximum normal stress, in psi, on the cylinder is given by Determine the maximum stress, in psi, with second order accuracy ! Program it ! 15

Metode Mencari Solusi Persamaan Diferensial Berderajat Tinggi – SPD DT 16

SPD - DT n n Dari metode Euler’s and Runge-Kutta untuk menyelesaikan pers diff biasa berderajat 1 dari bentuk : (1) Apa yang dilakukan untuk menyelesaikan persamaan diff simultan (pasangan) atau berderajat lebih tinggi ? Misalkan sebuah PDB : (2) 17

n Dengan kondisi awal diselesaikan dengan asumsi : (3. 1) (3. 2) (3. 3). . (3. n) 18

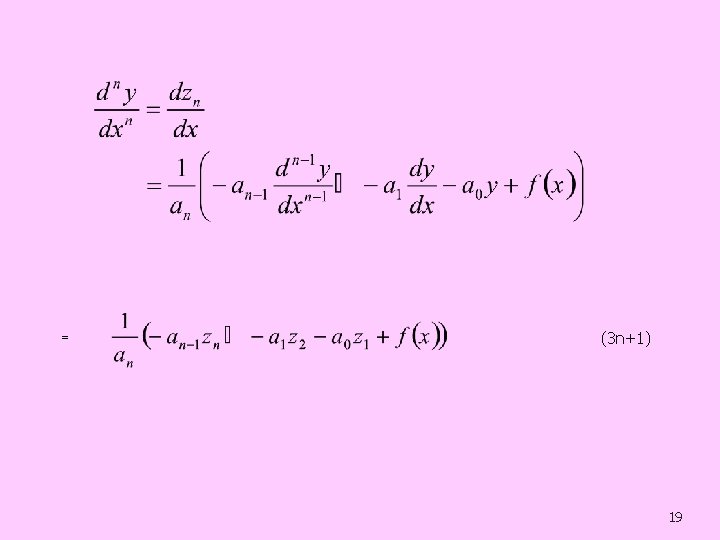
= (3 n+1) 19

Persamaan (3. 1) sampai (3. n+1) merepresentasikan persamaan diff berderajat 1 sebagai : (4. 1) (4. 2). . . . (4. n) n Setiap PDB berderajat 1 ditemani dengan satu kondisi awal. PDB berderajat 1 ini simultan tetapi dapat diselesaikan dengan PDB berderajat 1 yang sudah dipelajari. 20

Contoh 1 Dari PDB berderajat 1 : Solusi Diasumsikan : maka 21

Substitusikan dengan PDB berderajat 2 akan memberikan : Dua PDB simultan berderajat 1 bila dilengkapi dengan kondisi awal adalah : Salah satu dari metode numerik dapat digunakan untuk menyelesaikan PDB berderajat 1. 22

SOAL : Jika diberikan PDB tentukan dengan metode Euler’s : a) y(0, 75) b) absolute relative true error untuk part(a), if c) Gunakan 23