PDAs Push Down Automata CSCI 432 Computer Science

PDAs Push Down Automata CSCI 432 Computer Science Theory

Oversimplified Definition v a PDA is a FA with a stack v a PDA has states and transitions like a FA, but a PDA has memory

Why Should I Care? Ø Why a stack instead of an array or some other storage type? Ø Why is a FA with a stack useful in the real world?

PDA vs CFG • If a language is accepted by a PDA, then it is a CFG. • Remember: • FAs accept Regular Languages • CFGs accept both Regular and Non. Regular Languages.

Formal Definition A Pushdown Automaton is defined as a sextuple: Q finite set of states ∑ input alphabet Γ set of stack symbols s 0 ∈ Q the initial state F⊆Q set of favorable states Δ transition relations

Δ Rules ((current state, next input, current stack top), (new state, replace stack top with this)) Example: ((s, a, b), (t, c)) "If state is 's' && the next character is 'a' && the stack top is 'b'; then change state to 't' and replace the 'b' on the stack top with a 'c'. "

Δ Rules ((current state, next input, current stack top), (new state, replace stack top with this)) Example: ((s, a, b), (t, c)) s a, b→c t

Example Δ Rules ((s, a, e), (t, c)) If state==s && input==a && stack==anything Then state=t and push(c) ((s, e, e), (t, c)) If state==s && input==anything && stack==anything Then state=t and push(c) and do not consume any input

Example Δ Rules ((s, a, b), (t, e)) If state==s && input==a && stack==b Then state=t and pop(b) ((s, a, b), (t, ab)) If state==s && input==a && stack==b Then state=t and push(a)

PDA Example 1 L = { a nb n : n ∈ N } Q = { s 0, s, f } ∑ = {a, b} Γ={a} S 0 = s 0 F = { s 0, f } Δ = ((s 0, a, e), (s, a)) ((s, b, a), (f, e)) ((f, b, a), (f, e)) textbook pages 81 -83

PDA Example 1 Rules: ((s 0, a, e), (s, a)) ((s, b, a), (f, e)) ((f, b, a), (f, e)) Input: aabb state remaining input stack s 0 aabb e s abb a s bb aa f b a f e e

PDA Example 2 Rules: ((s 0, a, e), (s, a)) ((s, b, a), (f, e)) ((f, b, a), (f, e)) Input: aaabb state remaining input stack s 0 aaabb e s aabb a s abb aa s bb aaa f b aa f e a no rule for (f, e, a) so fail

PDA Example 3 Rules: ((s 0, a, e), (s, a)) ((s, b, a), (f, e)) ((f, b, a), (f, e)) Input: abb state remaining input stack s 0 abb e s bb a f b e no rule for (f, b, e) so fail

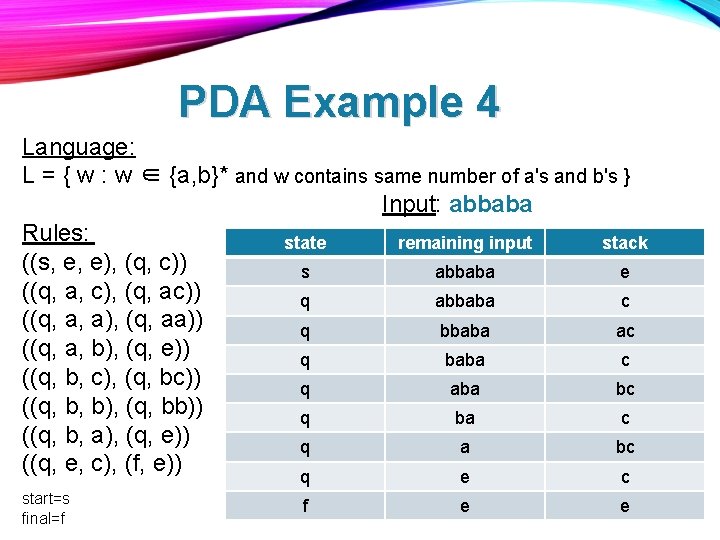
PDA Example 4 Language: L = { w : w ∈ {a, b}* and w contains same number of a's and b's } Input: abbaba Rules: state remaining input stack ((s, e, e), (q, c)) s abbaba e ((q, a, c), (q, ac)) q abbaba c ((q, a, a), (q, aa)) q bbaba ac ((q, a, b), (q, e)) q baba c ((q, b, c), (q, bc)) q aba bc ((q, b, b), (q, bb)) q ba c ((q, b, a), (q, e)) q a bc ((q, e, c), (f, e)) q e c start=s final=f f e e

Creating PDAs We can convert CFG rules into PDA rules S → blah o We need two states, p=start and q=running o The first rule is always ((p, e, e), (q, S)) o For each CFG rule A → x ((q, e, A), (q, x)) o For each a ∈ ∑ ((q, a, a), (q, e))

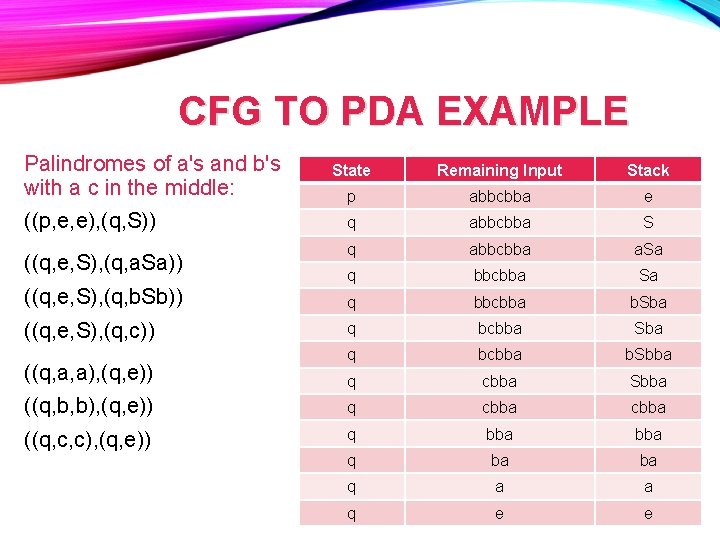
CFG TO PDA EXAMPLE Palindromes of a's and b's with a c in the middle: PDA: CFG: ((q, e, S), (q, a. Sa)) S → a. Sa S → b. Sb S→c ((q, e, S), (q, b. Sb)) ((p, e, e), (q, S)) ((q, e, S), (q, c)) ((q, a, a), (q, e)) ((q, b, b), (q, e)) ((q, c, c), (q, e))

CFG TO PDA EXAMPLE Palindromes of a's and b's with a c in the middle: State Remaining Input Stack p abbcbba e q abbcbba S q abbcbba a. Sa q bbcbba b. Sba q bcbba b. Sbba q cbba Sbba ((q, b, b), (q, e)) q cbba ((q, c, c), (q, e)) q bba q ba ba q a a q e e ((p, e, e), (q, S)) ((q, e, S), (q, a. Sa)) ((q, e, S), (q, b. Sb)) ((q, e, S), (q, c)) ((q, a, a), (q, e))

CFG TO PDA EXAMPLE Palindromes of a's and b's with a c in the middle: ((p, e, e), (q, S)) ((q, e, S), (q, a. Sa)) ((q, e, S), (q, b. Sb)) ((q, e, S), (q, c)) ((q, a, a), (q, e)) ((q, b, b), (q, e)) ((q, c, c), (q, e)) State Remaining Input Stack p abcab e q abcab S q abcab a. Sa q bcab b. Sba q cab cba q ab ba no rule for (q, a, b) so fail

So, now you know… • a CFG can be converted into a PDA • a PDA is a FA with a stack • How to write code to implement a FA • Regular Expressions and FAs are the same set of languages • So… • You should be able to combine all that to write code to implement a parser. • Or at least see that it is possible for Lex and YACC to write the code for you.