PCA vs ICA PCA Focus on uncorrelated and

  • Slides: 20
Download presentation
PCA vs ICA • PCA – Focus on uncorrelated and Gaussian components – Second-order

PCA vs ICA • PCA – Focus on uncorrelated and Gaussian components – Second-order statistics – Orthogonal transformation • ICA – Focus on independent and non-Gaussian components – Higher-order statistics – Non-orthogonal transformation

Independent Component Analysis (1/5) • Concept of ICA – A given signal(x) is generated

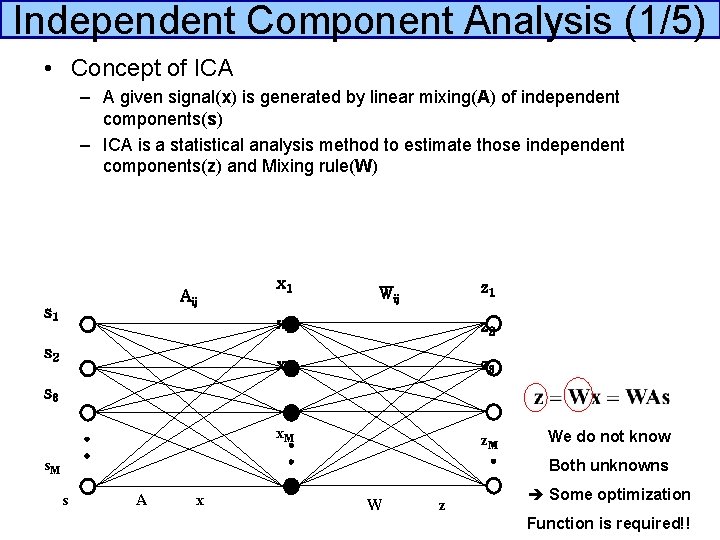
Independent Component Analysis (1/5) • Concept of ICA – A given signal(x) is generated by linear mixing(A) of independent components(s) – ICA is a statistical analysis method to estimate those independent components(z) and Mixing rule(W) Aij s 1 s 2 x 1 z 1 Wij x 2 z 2 x 3 z 3 x. M z. M s 3 s. M We do not know Both unknowns s A x W z Some optimization Function is required!!

Independent Component Analysis (2/5)

Independent Component Analysis (2/5)

Independent Component Analysis(3/5) • What is independent component? ? – If one variable can

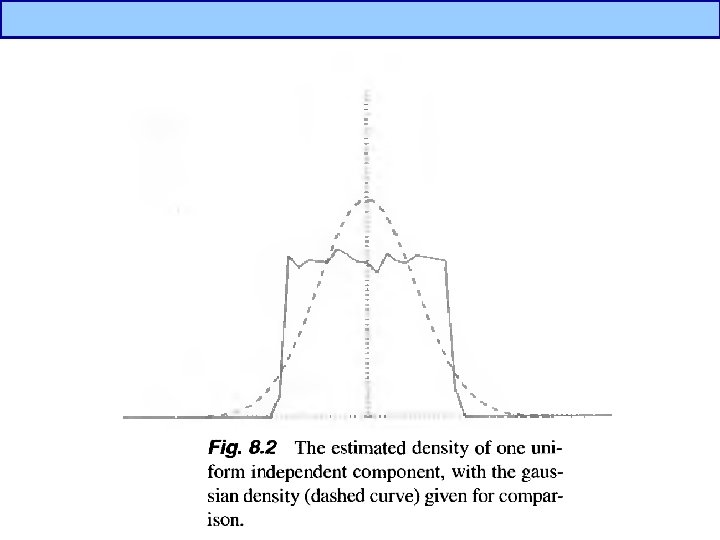
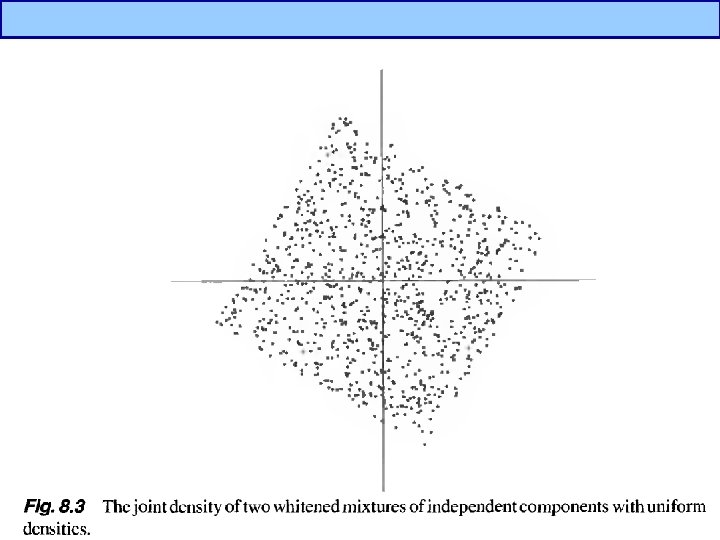
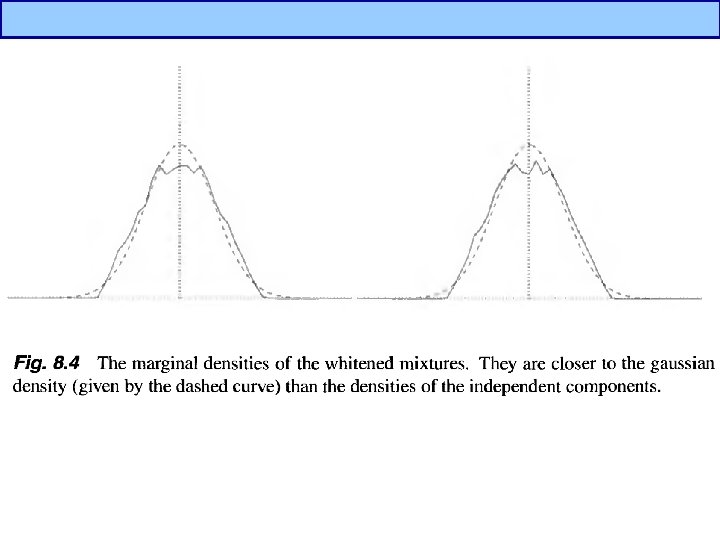
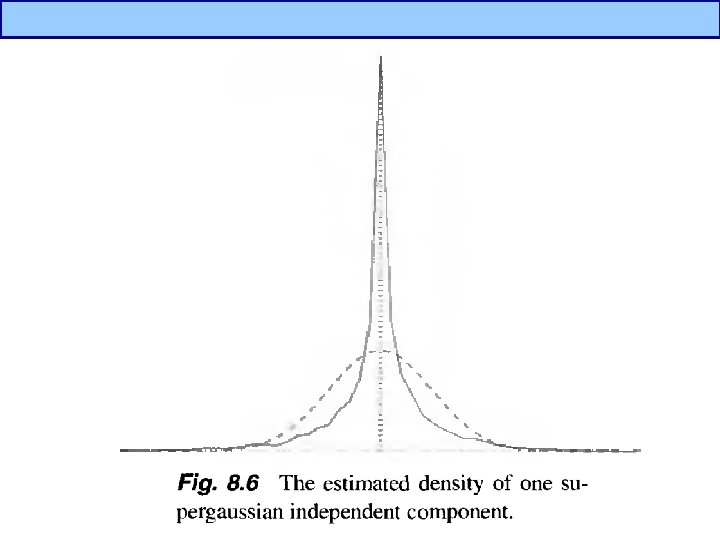
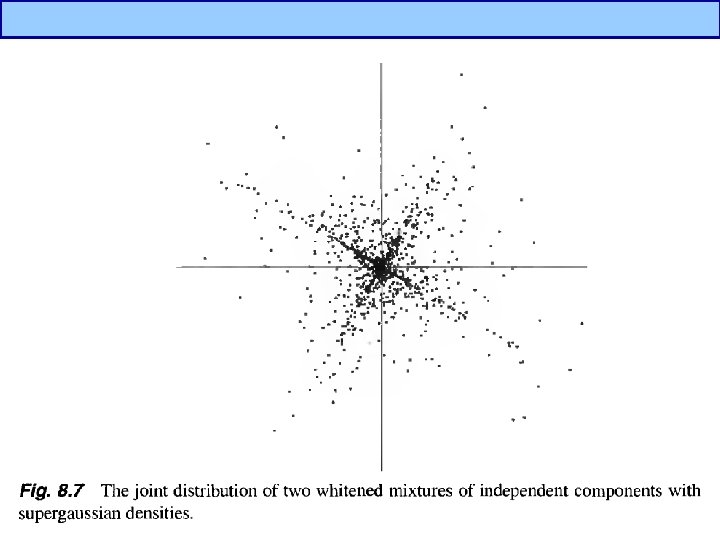
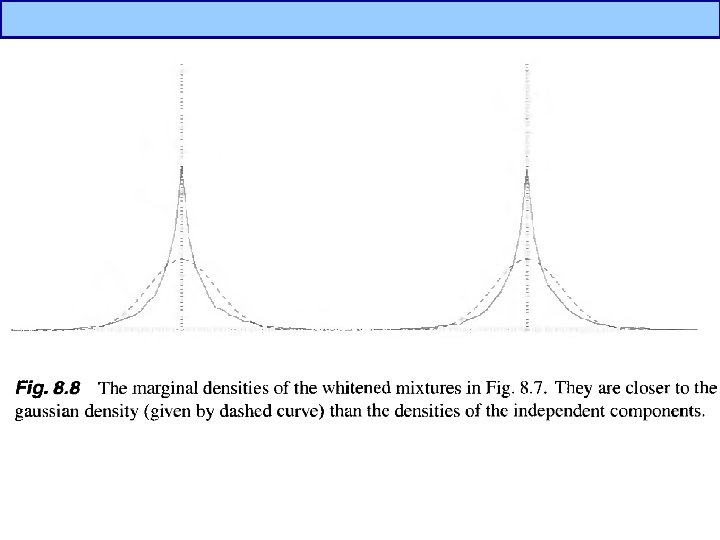
Independent Component Analysis(3/5) • What is independent component? ? – If one variable can not be estimated from other variables, it is independent. – By Central Limit Theorem, a sum of two independent random variables is more gaussian than original variables distribution of independent components are nongaussian – To estimate ICs, z should have nongaussian distribution, i. e. we should maximize nonguassianity.

Independent Component Analysis(4/5) • What is nongaussianity? – Supergaussian – Subgaussian – Low entropy

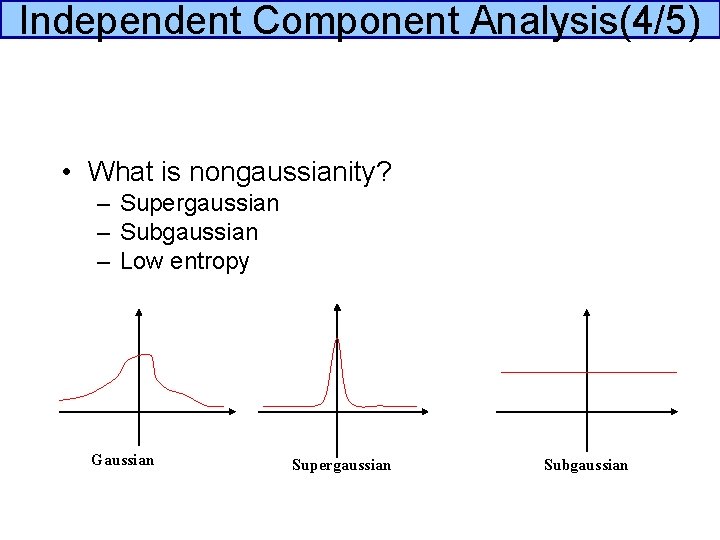
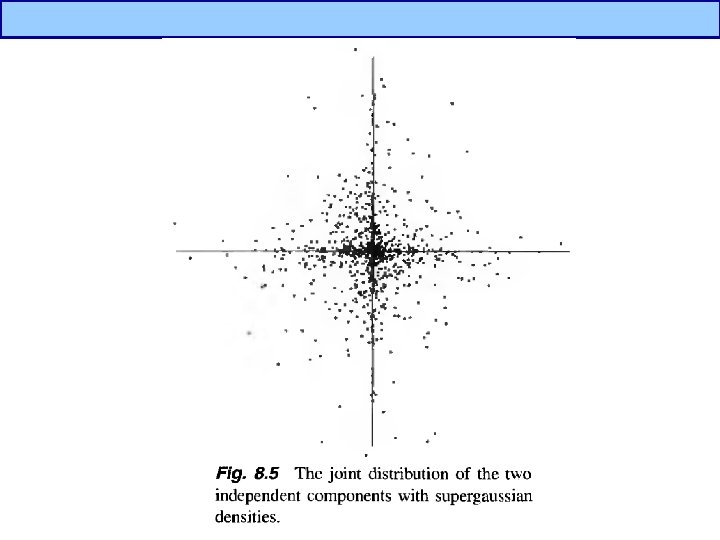
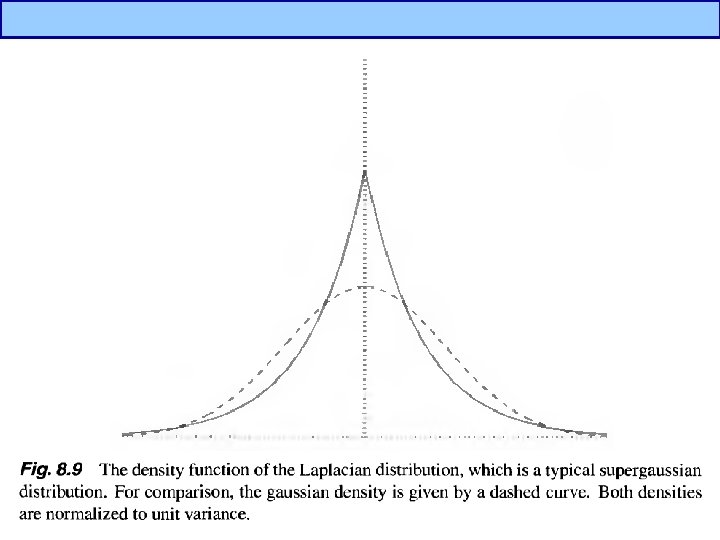
Independent Component Analysis(4/5) • What is nongaussianity? – Supergaussian – Subgaussian – Low entropy Gaussian Supergaussian Subgaussian

Independent Component Analysis(5/5) • Measuring nongaussianity by Kurtosis – Kurtosis : 4 th order

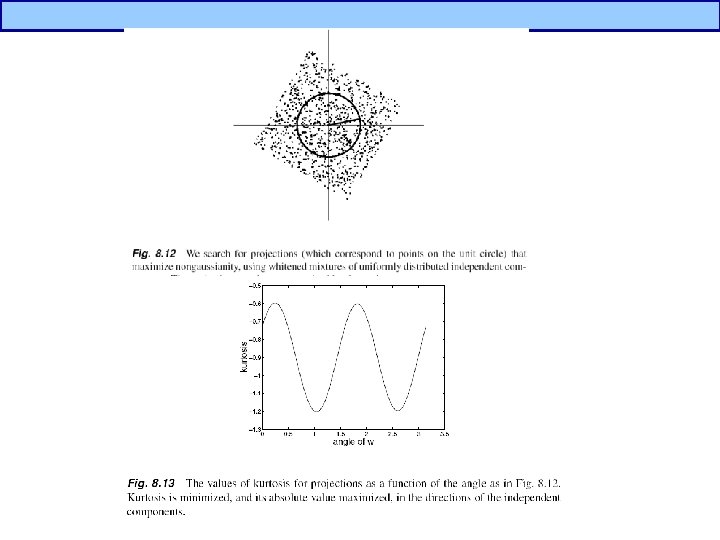
Independent Component Analysis(5/5) • Measuring nongaussianity by Kurtosis – Kurtosis : 4 th order cumulant of randomvariable • If kurt(z) is zero, gaussian • If kurt(z) is positive, supergaussian • If kurt(z) is negative, subgaussian • Maximzation of |kurt(z)| by gradient method Simply change The norm of w Fast-fixed point algorithm

PCA vs LDA vs ICA • PCA : Proper to dimension reduction • LDA

PCA vs LDA vs ICA • PCA : Proper to dimension reduction • LDA : Proper to pattern classification if the number of training samples of each class are large • ICA : Proper to blind source separation or classification using ICs when class id of training data is not available

References • Simon Haykin, “Neural Networks – A Comprehensive Foundation- 2 nd Edition, ”

References • Simon Haykin, “Neural Networks – A Comprehensive Foundation- 2 nd Edition, ” Prentice Hall • Marian Stewart Bartlett, “Face Image Analysis by Unsupervised Learning, ” Kluwer academic publishers • A. Hyvärinen, J. Karhunen and E. Oja, “Independent Component Analysis, ”, John Willy & Sons, Inc. • D. L. Swets and J. Weng, “Using Discriminant Eigenfeatures for Image Retrieval”, IEEE Trasaction on Pattern Analysis and Machine Intelligence, Vol. 18, No. 8, August 1996

Bmode ICA vs ECA ICA ECA ICA vsBmode ICA vs ECA ICA ECA ICA vs
ICA Alphan Altinok Outline PCA ICA Foundation AmbiguitiesICA Alphan Altinok Outline PCA ICA Foundation Ambiguities
Epidmiologie ICA ICA frquente et grave mortalit 12Epidmiologie ICA ICA frquente et grave mortalit 12
EX HOTEL DE TURISTAS DE ICA ENTORNO IcaEX HOTEL DE TURISTAS DE ICA ENTORNO Ica
Calendar of Events 2012 ICA Private event ICACalendar of Events 2012 ICA Private event ICA
PLANEACINDIDACT ICA PLANEACINDIDACT ICA INTERESES Y CONOCIMIENTOS PARTIRPLANEACINDIDACT ICA PLANEACINDIDACT ICA INTERESES Y CONOCIMIENTOS PARTIR
Integrated Context Analysis ICA Introducing the ICA WhatIntegrated Context Analysis ICA Introducing the ICA What
ICA Thing Model Introduction ICA Connectivity Alliance 2019ICA Thing Model Introduction ICA Connectivity Alliance 2019
EX HOTEL DE TURISTAS DE ICA ENTORNO IcaEX HOTEL DE TURISTAS DE ICA ENTORNO Ica
Master ICA Grenoble Information Cognition Apprentissages Master ICAMaster ICA Grenoble Information Cognition Apprentissages Master ICA
Dimensionality reduction PCA SVD MDS ICA and friendsDimensionality reduction PCA SVD MDS ICA and friends
A Quick Practical Guide to PCA and ICAA Quick Practical Guide to PCA and ICA
1 Bayesian belief networks 2 PCA and ICA1 Bayesian belief networks 2 PCA and ICA
Data Visualization By PCA LDA and ICA TsunYuData Visualization By PCA LDA and ICA TsunYu
Uncorrelated and Autocorrelated relaxed phylogenetics Michal DefoinPlatel andUncorrelated and Autocorrelated relaxed phylogenetics Michal DefoinPlatel and
Dimensionality reduction PCA MDS ISOMAP SVD ICA sDimensionality reduction PCA MDS ISOMAP SVD ICA s
Blind Source Separation PCA ICA HST 6 555Blind Source Separation PCA ICA HST 6 555
PCA vs ICA vs LDA How to representPCA vs ICA vs LDA How to represent
Blind Source Separation PCA ICA HST 582 J6Blind Source Separation PCA ICA HST 582 J6