PCA SVD Eigenvectors Applications Streaming Big Data Class

PCA, SVD, Eigenvectors, Applications, Streaming Big Data Class TAU 2013

Some Notation Big Data Class TAU 2013
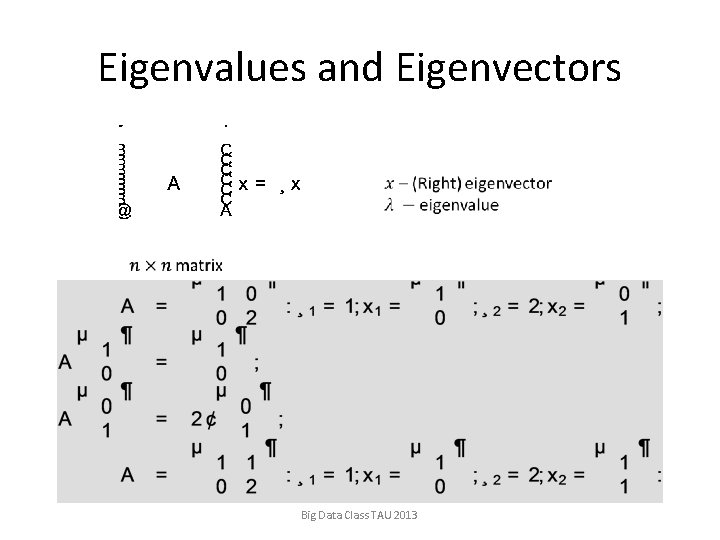
Eigenvalues and Eigenvectors Big Data Class TAU 2013

Eigenvalues and Eigenvectors Real valued matrices can have complex Eigenvalues/eigenvectors Big Data Class TAU 2013

Characteristic Polynomial Eigenvalues can be complex, and can appear multiple times Big Data Class TAU 2013

Example Big Data Class TAU 2013
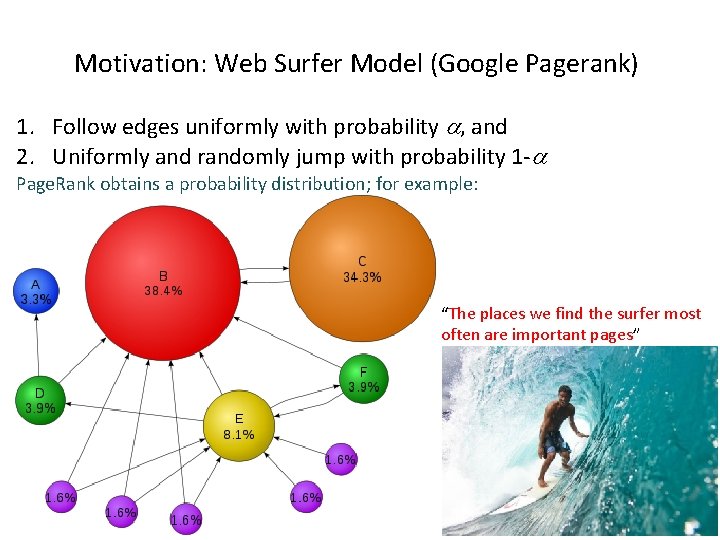
Motivation: Web Surfer Model (Google Pagerank) 1. Follow edges uniformly with probability , and 2. Uniformly and randomly jump with probability 1 - Page. Rank obtains a probability distribution; for example: “The places we find the surfer most often are important pages”

Stochastic Matrix of the (static) Web • 8

Pagerank = Eigenvector with eigenvalue 1 Big Data Class TAU 2013

Personalized Pagerank • Big Data Class TAU 2013

Stochastic Matrix For Personalized Pagerank • Right eigenvector with eigenvalue one gives personalized pagerank 11

More Properties of eigenvectors/values • Big Data Class TAU 2013

More Properties of eigenvectors/values • Eigenvalues of (real) symmetric matrices are real A real Big Data Class TAU 2013

More Properties of eigenvectors/values • Eigenvectors of two different eigenvalues of a symmetric (real) matrix are orthogonal Eigenvectors belonging to distinct eigenvalues are linearly independent Big Data Class TAU 2013

Properties of eigenvectors/values • Big Data Class TAU 2013

Transformations • Big Data Class TAU 2013

Power iteration Assumes that A is full rank Alternative: normalize Big Data Class TAU 2013

Tricks • Big Data Class TAU 2013

Principle Component Analysis • Big Data Class TAU 2013

Singular Value Decomposition (SVD)

1 at position j
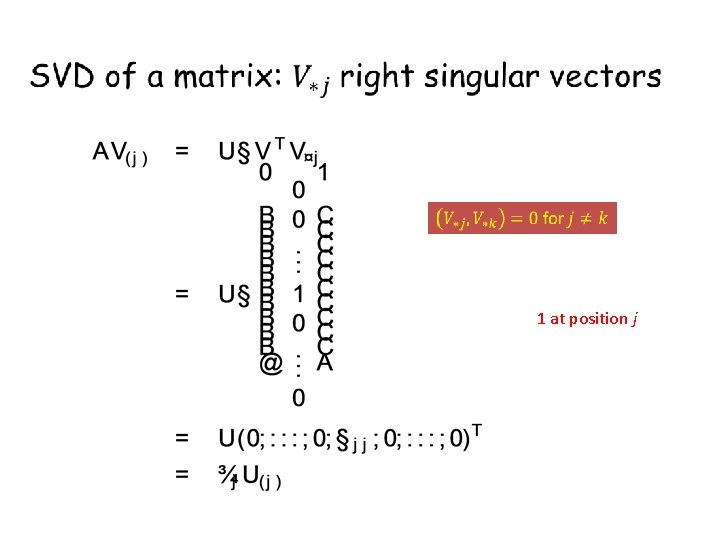
1 at position j

SVD Column times row gives matrix Big Data Class TAU 2013

Pagerank vs. Hubs and Authorities • Pagerank (and personalized pagerank) are the right eigenvector of a stochastic matrix for a random walk in the web • Pagerank can be interpreted as follows: – The importance of a node is the sum of the importance of the nodes that point to it (split amongst all nodes it points to). • Hubs and Authorities: A different idea, (SVD) – Hub nodes confer authority to “authorities” – This is not split amongst the outdegree – Authorities confer “hub quality” to hubs Big Data Class TAU 2013
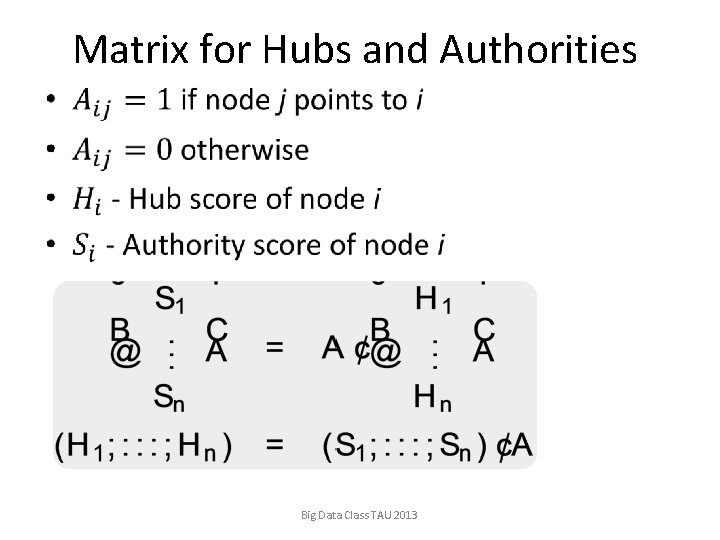
Matrix for Hubs and Authorities • Big Data Class TAU 2013

SVD and Eigenvalues Big Data Class TAU 2013

SVD and Eigenvalues Big Data Class TAU 2013

SVD and eigenvectors • Big Data Class TAU 2013
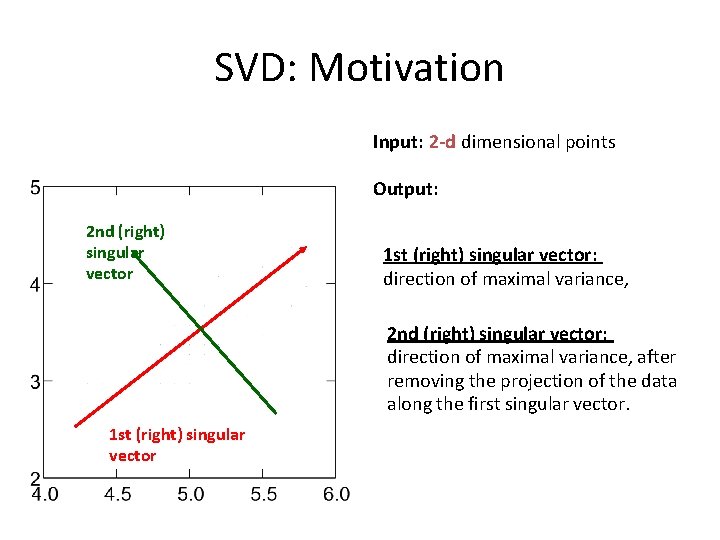
SVD: Motivation Input: 2 -d dimensional points Output: 2 nd (right) singular vector 1 st (right) singular vector: direction of maximal variance, 2 nd (right) singular vector: direction of maximal variance, after removing the projection of the data along the first singular vector. 1 st (right) singular vector
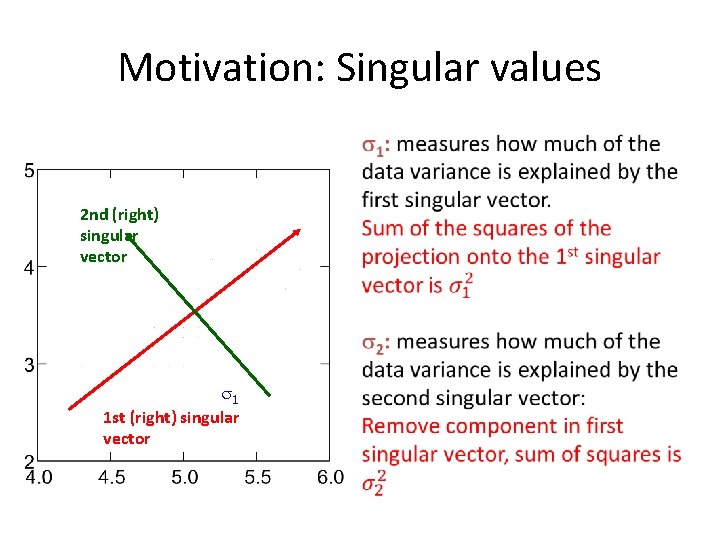
Motivation: Singular values 2 nd (right) singular vector 1 1 st (right) singular vector
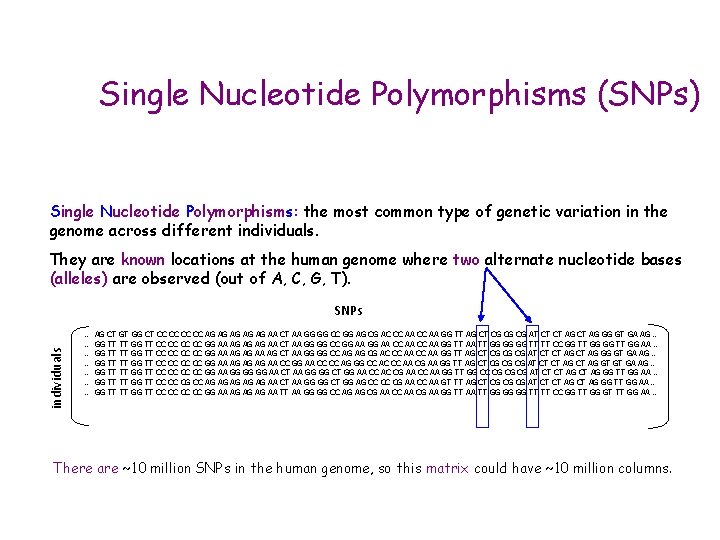
Single Nucleotide Polymorphisms (SNPs) Single Nucleotide Polymorphisms: the most common type of genetic variation in the genome across different individuals. They are known locations at the human genome where two alternate nucleotide bases (alleles) are observed (out of A, C, G, T). individuals SNPs … … … … AG CT GT GG CT CC CC AG AG AG AA CT AA GG GG CC GG AG CG AC CC AA GG TT AG CT CG CG CG AT CT CT AG GG GT GA AG … GG TT TT GG TT CC CC GG AA AG AG AG AA CT AA GG GG CC GG AA CC AA GG TT AA TT GG GG GG TT TT CC GG TT GG AA … GG TT TT GG TT CC CC GG AA AG AG AA AG CT AA GG GG CC AG AG CG AC CC AA GG TT AG CT CG CG CG AT CT CT AG GG GT GA AG … GG TT TT GG TT CC CC GG AA AG AG AG AA CC GG AA CC CC AG GG CC AC CC AA CG AA GG TT AG CT CG CG CG AT CT CT AG GT GT GA AG … GG TT TT GG TT CC CC GG AA GG GG GG AA CT AA GG GG CT GG AA CC AC CG AA CC AA GG TT GG CC CG CG CG AT CT CT AG GG TT GG AA … GG TT TT GG TT CC CC CG CC AG AG AG AA CT AA GG GG CT GG AG CC CC CG AA CC AA GT TT AG CT CG CG CG AT CT CT AG GG TT GG AA … GG TT TT GG TT CC CC GG AA AG AG AG AA TT AA GG GG CC AG AG CG AA CC AA CG AA GG TT AA TT GG GG GG TT TT CC GG TT GG GT TT GG AA … There are ~10 million SNPs in the human genome, so this matrix could have ~10 million columns.
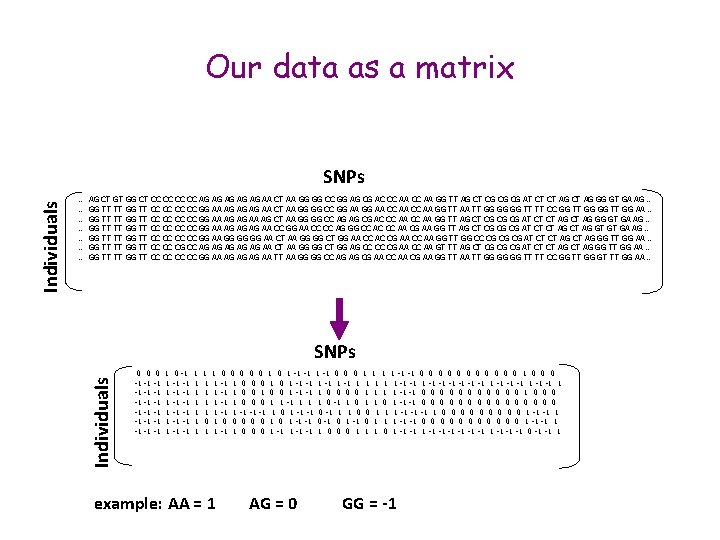
Our data as a matrix … … … … AG CT GT GG CT CC CC AG AG AG AA CT AA GG GG CC GG AG CG AC CC AA GG TT AG CT CG CG CG AT CT CT AG GG GT GA AG … GG TT TT GG TT CC CC GG AA AG AG AG AA CT AA GG GG CC GG AA CC AA GG TT AA TT GG GG GG TT TT CC GG TT GG AA … GG TT TT GG TT CC CC GG AA AG AG AA AG CT AA GG GG CC AG AG CG AC CC AA GG TT AG CT CG CG CG AT CT CT AG GG GT GA AG … GG TT TT GG TT CC CC GG AA AG AG AG AA CC GG AA CC CC AG GG CC AC CC AA CG AA GG TT AG CT CG CG CG AT CT CT AG GT GT GA AG … GG TT TT GG TT CC CC GG AA GG GG GG AA CT AA GG GG CT GG AA CC AC CG AA CC AA GG TT GG CC CG CG CG AT CT CT AG GG TT GG AA … GG TT TT GG TT CC CC CG CC AG AG AG AA CT AA GG GG CT GG AG CC CC CG AA CC AA GT TT AG CT CG CG CG AT CT CT AG GG TT GG AA … GG TT TT GG TT CC CC GG AA AG AG AG AA TT AA GG GG CC AG AG CG AA CC AA CG AA GG TT AA TT GG GG GG TT TT CC GG TT GG GT TT GG AA … SNPs Individuals SNPs 0 -1 -1 -1 0 -1 -1 -1 1 1 1 1 0 -1 -1 -1 -1 1 1 1 0 1 1 1 1 example: ΑΑ = 1 0 -1 -1 0 1 1 0 1 0 0 -1 0 0 1 0 1 -1 -1 0 0 0 1 1 -1 -1 0 0 0 1 0 0 0 1 -1 -1 1 1 -1 -1 -1 1 -1 -1 1 0 0 1 1 -1 -1 0 0 0 1 0 0 0 1 1 -1 1 0 1 -1 -1 0 0 0 0 -1 -1 1 0 1 -1 -1 0 -1 1 1 0 0 1 1 1 -1 -1 -1 1 0 0 0 0 0 1 -1 -1 1 0 0 1 -1 -1 0 1 1 1 -1 -1 0 0 0 1 -1 -1 1 0 0 0 1 1 1 0 1 -1 -1 1 -1 -1 -1 0 -1 -1 1 ΑG = 0 GG = -1

Rank-k approximations (Ak)

Rank-k approximations (Ak)

Uk solves an optimization problem… Given an m£n matrix A, we seek an m-by-k matrix C that minimizes the residual Frobenius norm:

Vk solves an optimization problem… Given an m£n matrix A, we seek an m-by-k matrix C that minimizes the residual Frobenius norm:
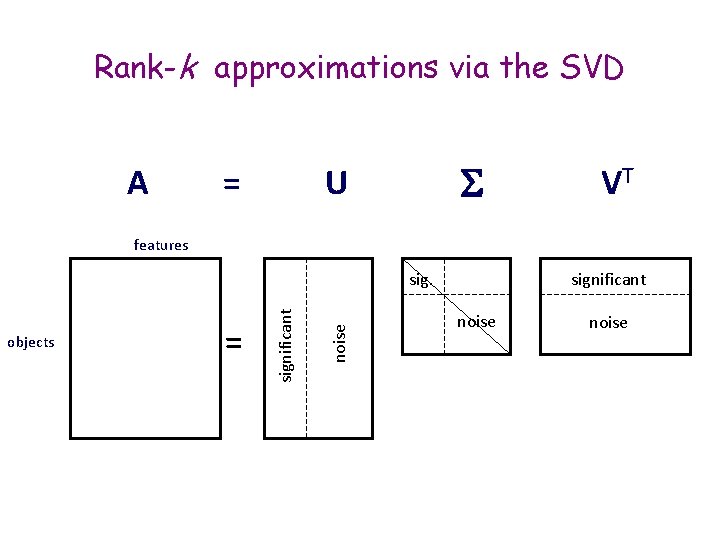
Rank-k approximations via the SVD A = U VT features = noise objects significant noise

SVD issues … SVD and PCA are often used to summarize and approximate matrices and they have enjoyed enormous success in data analysis. BUT

SVD issues … SVD and PCA are often used to summarize and approximate matrices and they have enjoyed enormous success in data analysis. BUT - For large sparse graphs they require large amounts of memory, exactly because the resulting matrices are not sparse any more. (Common networks such as the web, the Internet topology graph, the who-trusts-whom social network are all large and sparse. ) - Running time becomes an issue. - Assigning “meaning” to the singular vectors (reification) is tricky …

SVD Application: Document Retrieval The Vector Space Method • Term (rows) by document (columns) matrix, based on occurrence • translate into vectors in a vector space – one vector for each document • cosine to measure distance between vectors (documents) – small angle = large cosine = similar – large angle = small cosine = dissimilar

The Problem • Two problems using the vector space model: – synonymy: many ways to refer to the same object, e. g. car and automobile • leads to poor recall – polysemy: most words have more than one distinct meaning, e. g. model, python, chip • leads to poor precision
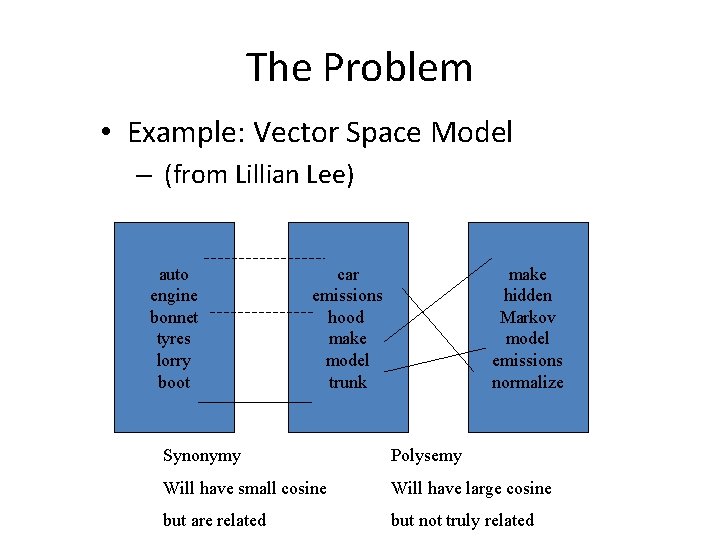
The Problem • Example: Vector Space Model – (from Lillian Lee) auto engine bonnet tyres lorry boot car emissions hood make model trunk make hidden Markov model emissions normalize Synonymy Polysemy Will have small cosine Will have large cosine but are related but not truly related

The Problem • Latent Semantic Indexing was proposed to address these two problems with the vector space model for Information Retrieval

Latent Semantic Analysis by Example • To see how this works let’s look at a small example • This example is taken from: Deerwester, S. , Dumais, S. T. , Landauer, T. K. , Furnas, G. W. and Harshman, R. A. (1990). "Indexing by latent semantic analysis. " Journal of the Society for Information Science, 41(6) , 391 -407. • Slides are from a presentation by Tom Landauer and Peter Foltz

A Small Example Technical Memo Titles c 1: Human machine interface for ABC computer applications c 2: A survey of user opinion of computer system response time c 3: The EPS user interface management system c 4: System and human system engineering testing of EPS c 5: Relation of user perceived response time to error measurement m 1: The generation of random, binary, ordered trees m 2: The intersection graph of paths in trees m 3: Graph minors IV: Widths of trees and well-quasi-ordering m 4: Graph minors: A survey

A Small Example – 2

A Small Example – 3 • Singular Value Decomposition {A}={U}{S}{V}T • Dimension Reduction {~A}~={~U}{~S}{~V}T
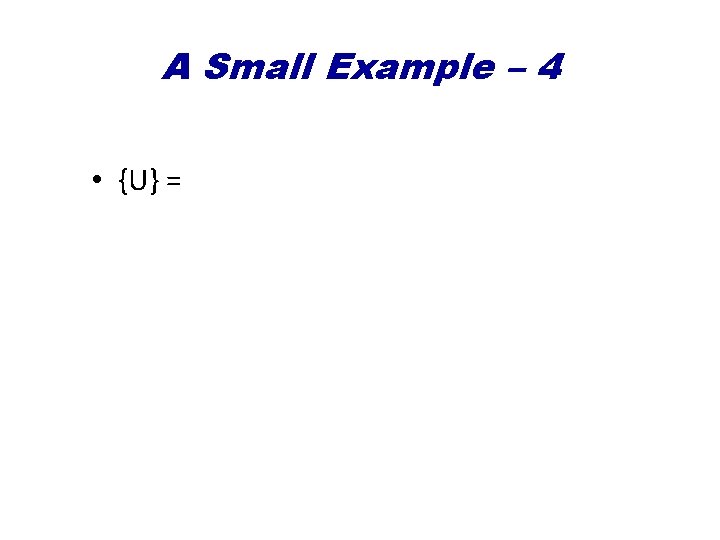
A Small Example – 4 • {U} =

A Small Example – 5 • {S} =
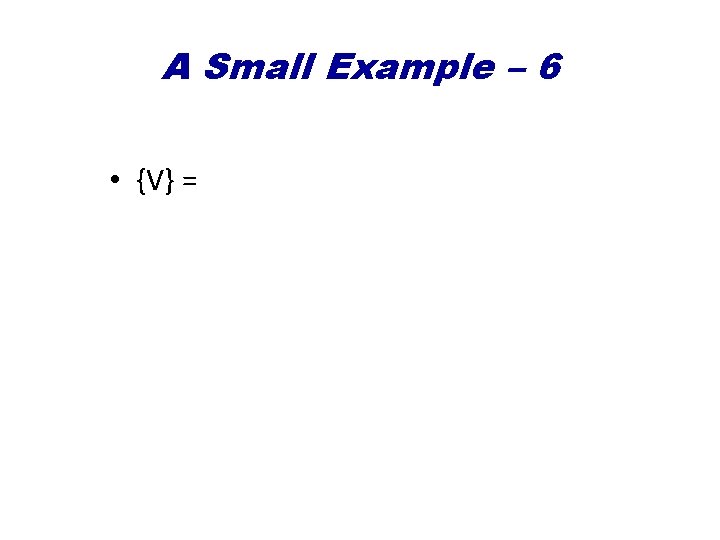
A Small Example – 6 • {V} =

A Small Example – 7

0. 92 -0. 72 1. 00

Lecture 8: More about Streaming Dimension Reduction Big Data Class TAU 2013

Again: Rank-k approximations (Ak)

Uk solves an optimization problem… Given an m£n matrix A, we seek an m-by-k matrix C that minimizes the residual Frobenius norm:

Vk solves an optimization problem… Given an m£n matrix A, we seek an m-by-k matrix C that minimizes the residual Frobenius norm:

Proofs of some claims Big Data Class TAU 2013

Big Data Class TAU 2013

Some claims Big Data Class TAU 2013

Streaming SVD: A appears row by row • Paper by Edo Liberty: Simple and Deterministic Matrix Sketches, KDD – “Frequent Directions” Algorithm – Extension of Misra-Gries • Paper by Mina Ghashami and Jeff Phillips: Relative Errors for Deterministic Low-Rank Matrix Approximations, preprint, uses “Frequent directions” Big Data Class TAU 2013

Lets study the SVD of few matrices

Lets study the SVD of few matrices

Lets study the SVD of few matrices

Lets study the SVD of few matrices

Lets study the SVD of few matrices Need to find the eigenvectors/eigenvalues of this matrix. .

Lets study the SVD of few matrices

Streaming Suggestion: Incremental PCA • Assume after i-1 rows we have the rank k approximation Ai-1 • Add the new row to Ai-1, compute the SVD of this new matrix and truncate it down to the k largest singular values

Incremental PCA: Problematic Example on whiteboard

• Big Data Class TAU 2013

• Big Data Class TAU 2013

Relative Error Heavy Hitters (Misra-Gries) • Big Data Class TAU 2013

Relative Error Heavy Hitters (Misra-Gries) • Big Data Class TAU 2013

• Big Data Class TAU 2013

Edo Liberty: Frequent directions • Big Data Class TAU 2013

Edo Liberty: Frequent directions SVD – change of notation because of GP paper Big Data Class TAU 2013

Edo Liberty: Frequent directions SVD – change of notation because of GP paper Reduce all singular values Big Data Class TAU 2013

Edo Liberty: Frequent directions SVD – change of notation because of GP paper Reduce all singular values Big Data Class TAU 2013

• Big Data Class TAU 2013

• This ends the proof of the original frequent directions Big Data Class TAU 2013

• Big Data Class TAU 2013

Lemma: This ends the proof of the original frequent directions Big Data Class TAU 2013

Sampling for approximate SVD • Fast Monte Carlo Algorithms for finding Low. Rank Approximations, Freize, Kannan, Vempala Big Data Class TAU 2013

Sampling assumption • Sample the rows of A so that row i is sampled with probability Big Data Class TAU 2013

A small sample contains a good approximation • Big Data Class TAU 2013

A small sample S contains a good approximation Big Data Class TAU 2013

A small sample S contains a good approximation Big Data Class TAU 2013

A small sample S contains a good approximation Projecting to subspaces does not depend on the basis Big Data Class TAU 2013

Bound the expected squared distance Big Data Class TAU 2013

References • Paper by Edo Liberty: Simple and Deterministic Matrix Sketches, KDD – “Frequent Directions” Algorithm – Extension of Misra-Gries • Paper by Mina Ghashami and Jeff Phillips: Relative Errors for Deterministic Low-Rank Matrix Approximations, preprint, uses “Frequent directions” Big Data Class TAU 2013
- Slides: 89